AMPLIAMENTO DELLA RETTA REALE ---> INDICE
Si
ricorda che in precedenza è stata considerata l'applicazione f, che ad ogni
punto della retta r associa un numero reale, e che tale applicazione è una bigezione.
Si considerano ora, oltre ai numeri reali, anche i numeri complessi, la cui forma è del tipo
x + iy,
in cui
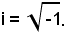
Si indichi a tal punto con C l'insieme dei numeri complessi, e si noti che l'insieme dei numeri reali è della forma
x + i0.
Si può dire che l'insieme dei numeri reali è una parte dell'insieme dei numeri complessi, cioè
R C.
C.
Si amplia ora la retta euclidea in modo tale che la retta r si possa considerare in corrispondenza bigettiva con i numeri complessi.
Allo scopo si considera una generica trasformazione lineare intera:
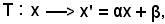
con
α R, β
R, β R, α ≠ 0.
R, α ≠ 0.
Si estende la trasformazione ampliando il dominio di definizione di T, cioè si considera x variabile in tutto l'insieme dei numeri complessi, quindi anche x' è un numero complesso.
Si indichi la nuova trasformazione lineare intera con:
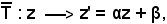
in cui z è un numero complesso, cioè
z C.
C.
 è la trasformazione lineare intera dell'insieme dei numeri complessi in x, α e β sono però numeri reali.
è la trasformazione lineare intera dell'insieme dei numeri complessi in x, α e β sono però numeri reali.
Si supponga che
z = x + iy,
quindi
z' = α(x + iy) + β = (αx + β) + i(αy),
in cui αx + β è la parte reale ed i(αy) è il numero complesso. Pertanto è dimostrato che la trasformazione lineare dei numeri complessi dà numeri complessi.
La trasformazione si chiama estensione complessa della trasformazione lineare intera T.
si chiama estensione complessa della trasformazione lineare intera T.
Assegnati una retta r, un riferimento (O, U) ed un sistema coordinato f di X in x
(O, U) ed un sistema coordinato f di X in x R, si consideri la riunione di r ed r' indicata con:
R, si consideri la riunione di r ed r' indicata con:
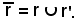
Si consideri inoltre la bigezione
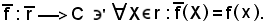
E' noto che tutte le bigezioni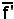 sono uguali al prodotto di
sono uguali al prodotto di  per
per 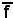 , cioè
, cioè
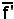 =
= 
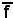 .
.
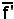 si chiama estensione complessa sulla retta euclidea r.
si chiama estensione complessa sulla retta euclidea r.
OsservazioneConsiderata una generica trasformazione lineare intera:
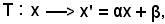
se α = 1 e β = 0, essa trasforma ogni numero in se stesso, in quanto si ha x = x'.
Ciò osservato, nel caso specifico risulta
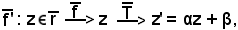
se α = 1 e β = 0, si ha:
z' = z,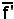 =
= 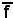 .
.
Si è pervenuti ad un risultato notevole, cioè che fra tutte le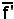 c'è anche
c'è anche 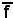 .
.
Gli elementi appartenenti ad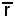 si chiamano punti.
si chiamano punti.
Gli elementi appartenenti ad r si chiamano punti reali.
Gli elementi appartenenti ad r' si chiamano punti complessi non reali.
Quale che sia il sistema coordinato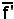 , i punti di r hanno ascissa reale, mentre quelli di r' hanno per ascissa un numero complesso non reale, cioè
, i punti di r hanno ascissa reale, mentre quelli di r' hanno per ascissa un numero complesso non reale, cioè
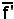 (Z) = z
(Z) = z C,
C,
dove z è l'ascissa del punto Z del sistema coordinato prescelto.Si considerino ora
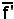 =
= 
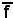 ,
,
 Z
Z
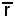 :
: 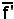 (Z)
(Z) C,
C,
e poi
E' noto che
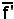 (X) =
(X) =  (
(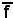 (X)) =
(X)) =  (f(x)) =
(f(x)) =  (x),
(x),
poichè
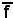 (X) = f(x), f(X) = x
(X) = f(x), f(X) = x R.
R.
Siccome la trasformazione lineare intera era definita da
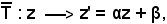
in cui
α R, β
R, β R, α ≠ 0,
R, α ≠ 0,
essendo in tal caso
z = x R,
R,
si ha che
 (x)
(x) R,
R,
cioè
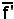 (X)
(X)
è sempre un numero reale, come volevasi dimostrare.
Estensione delle proprietà sulla retta euclidea
Definizione 1
Considerati la coppia ordinata (Z1, Z2) di punti complessi ed il segmento orientato Z1Z2, si può definire la misura del segmento orientato Z1Z2, come la differenza delle ascisse z1 e z2 rispetto al sistema coordinato assegnato, cioè
Z1Z2 = z2 - z1.
Definizione 2
Considerati Z1, Z2 punti dell'estensione complessa, essi si dicono complessi e coniugati se le loro ascisse sono numeri complessi e coniugati in un sistema coordinato qualsiasi.
Si dimostra che due punti, che hanno per ascisse numeri complessi e coniugati, hanno per ascisse numeri complessi e coniugati in un sistema coordinato qualsiasi.
Ciò prova anche che trasforma i numeri complessi e coniugati in altri numeri complessi e coniugati.
trasforma i numeri complessi e coniugati in altri numeri complessi e coniugati.
Infatti, considerati i numeri complessi e coniugati x + iy ed x - iy, essendo in generale che
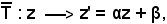
in cui z è un numero complesso, si ha che:
il trasformato del primo numero complesso è z' = α(x + iy) + β = αx + β + iαy,
il trasformato del secondo numero complesso è z'' = α(x - iy) + β = αx + β - iαy,
e ciò dimostra che anche i trasformati sono numeri complessi e coniugati.
Definizione 3
Considerata una terna ordinata di numeri complessi Z1, Z2, Z3, Z2 ≠ Z3, si chiama rapporto semplice il numero definito da
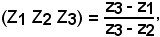
dove z1, z2, z3 sono le ascisse in un determinato sistema coordinato, ed anche se il riferimento (O, U) cambia in
(O, U) cambia in  (O', U'), esso non varia.
(O', U'), esso non varia.
Punto medio tra due punti dell'estensione complessa
Z3 è punto medio tra Z1 e Z2, se il rapporto semplice della terna ordinata Z1, Z2, Z3 è uguale a -1, cioè
(Z1 Z2 Z3) = -1.
Si può quindi dedurre l'ascissa del punto medio di un'estensione complessa con dimostrazione analoga a quella della retta reale.
Il punto medio fra due punti complessi e coniugati è un numero reale.
Infatti, sia Z un punto complesso, in un sistema coordinato qualsiasi che abbia ascissa x + iy, e Z' un altro punto complesso, di ascissa x - iy. L'ascissa del punto medio, indicata con M(X) è data dalla semisomma delle due, cioè:
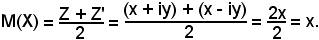
Gruppo di trasformazioni
Si supponga che E sia un insieme di elementi e Φ un insieme di trasformazioni di E in E, ossiadi bigezioni di E in E. Si dice che Φ è un gruppo di trasformazioni se
a) f
f Φ,
Φ,  g
g Φ : f ο g
Φ : f ο g Φ, cioè per ogni coppia di trasformazioni di Φ il loro prodotto appartiene a Φ;
Φ, cioè per ogni coppia di trasformazioni di Φ il loro prodotto appartiene a Φ;
b) f
f Φ : f-1
Φ : f-1 Φ, cioè per ogni trasformazione di Φ la trasformazione inversa appartiene a Φ.
Φ, cioè per ogni trasformazione di Φ la trasformazione inversa appartiene a Φ.
Si deduce subito che a Φ appartiene la trasformazione identica, che ad ogni elemento di E fa corrispondere lo stesso elemento.
Infatti, considerato f Φ, per la a) si ha
Φ, per la a) si ha
f-1ο f Φ,
Φ,
mentre per la b)
f-1 Φ.
Φ.
Si vuole vedere ora come si definisce f-1ο f e, allo scopo, si costruisce il seguente diagramma:
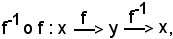
quindi
f-1ο f = i, f ο f-1 = i
e risulta
f ο i = i ο f,
cioè i funziona da elemento neutro.
Si dimostra ora che l'insieme di tutte le trasformazioni lineari intere sull'insieme dei reali è un gruppo di trasformazioni e, similmente, l'insieme di tutte le estensioni complesse delle trasformazioni lineari intere è un gruppo di trasformazioni.Si supponga che Φ sia l'insieme di tutte le trasformazioni lineari intere sull'insieme dei reali, cioè
f Φ
Φ 
 α
α R, β
R, β R, α ≠ 0,
R, α ≠ 0, 
 x
x R : f(x) = αx + β.
R : f(x) = αx + β.
Per dimostrare che l'insieme di tutte le trasformazioni lineari intere sull'insieme dei reali è un gruppo di trasformazioni, occorre dimostrare che:
1) il prodotto di due trasformazioni lineari intere è una trasformazione lineare intera.
2) l'inversa di una trasformazione lineare intera è una trasformazione lineare intera.
Dimostrazione 1)
Si considerino due trasformazioni lineari intere:
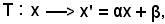
con
α R, β
R, β R, α ≠ 0
R, α ≠ 0
e
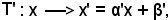
con
α' R, β'
R, β' R, α' ≠ 0.
R, α' ≠ 0.
Si deve dimostrare che il prodotto T'T, o la componente delle due trasformazioni, è una trasformazione lineare intera.
Se x è il generico numero reale, ad esso si fa corrispondere mediante T il numero reale αx + β, quindi
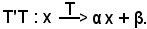
Si consideri ora il trasformato di αx + β mediante T', che è dato da αx + β + β', quindi
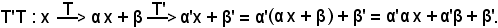
Pertanto, T'T trasforma il generico x, come segue:
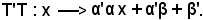
Si pongono ora
α'α = α'', α'β + β' = β'',
e, sostituendo nella relazione suddetta, si ha:
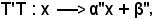
con
α'' R, β''
R, β'' R, α'' ≠ 0.
R, α'' ≠ 0.
E' quindi dimostrato che il il prodotto di due trasformazioni lineari intere è una trasformazione lineare intera, cioè questa è la prima proprietà che soddisfa un gruppo di trasformazioni.
Dimostrazione 2)
Si consideri una generica trasformazione lineare intera:
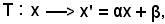
con
α R, β
R, β R, α ≠ 0.
R, α ≠ 0.
Si fissi un elemento y per poter trovare l'y' che ha come corrispondente y nella trasformazione T, quindi si ha
y = αy' + β,
da cui
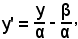
pertanto risulta
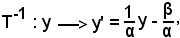
e quindi si può dire che il generico x è trasformato dall'inverso di T in
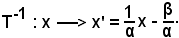
Indicando a tal punto
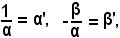
si ottiene che la trasformazione inversa è dello stesso tipo della trasformazione lineare intera, quindi
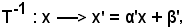
con
α' R, β'
R, β' R, α' ≠ 0.
R, α' ≠ 0.
E' quindi dimostrato anche che l'inversa di una trasformazione lineare intera è una trasformazione lineare intera, e quindi l'insieme di tutte le trasformazioni lineari intere sull'insieme dei reali è un gruppo di trasformazioni, anche quando si considera l'insieme di tutte le estensioni complesse delle trasformazioni lineari intere, ferme restanti le condizioni
α R, β
R, β R, α ≠ 0.
R, α ≠ 0.
Si considerano ora, oltre ai numeri reali, anche i numeri complessi, la cui forma è del tipo
x + iy,
in cui
Si indichi a tal punto con C l'insieme dei numeri complessi, e si noti che l'insieme dei numeri reali è della forma
x + i0.
Si può dire che l'insieme dei numeri reali è una parte dell'insieme dei numeri complessi, cioè
R
Si amplia ora la retta euclidea in modo tale che la retta r si possa considerare in corrispondenza bigettiva con i numeri complessi.
Allo scopo si considera una generica trasformazione lineare intera:
con
α
Si estende la trasformazione ampliando il dominio di definizione di T, cioè si considera x variabile in tutto l'insieme dei numeri complessi, quindi anche x' è un numero complesso.
Si indichi la nuova trasformazione lineare intera con:
in cui z è un numero complesso, cioè
z
Si supponga che
z = x + iy,
quindi
z' = α(x + iy) + β = (αx + β) + i(αy),
in cui αx + β è la parte reale ed i(αy) è il numero complesso. Pertanto è dimostrato che la trasformazione lineare dei numeri complessi dà numeri complessi.
La trasformazione
Assegnati una retta r, un riferimento
Si consideri inoltre la bigezione
E' noto che tutte le bigezioni
Osservazione
se α = 1 e β = 0, essa trasforma ogni numero in se stesso, in quanto si ha x = x'.
Ciò osservato, nel caso specifico risulta
se α = 1 e β = 0, si ha:
z' = z,
Si è pervenuti ad un risultato notevole, cioè che fra tutte le
Gli elementi appartenenti ad
Gli elementi appartenenti ad r si chiamano punti reali.
Gli elementi appartenenti ad r' si chiamano punti complessi non reali.
Quale che sia il sistema coordinato
dove z è l'ascissa del punto Z del sistema coordinato prescelto.Si considerino ora
e poi
X r.
r.
E' noto che
poichè
Siccome la trasformazione lineare intera era definita da
in cui
α
essendo in tal caso
z = x
si ha che
cioè
è sempre un numero reale, come volevasi dimostrare.
Estensione delle proprietà sulla retta euclidea
Definizione 1
Considerati la coppia ordinata (Z1, Z2) di punti complessi ed il segmento orientato Z1Z2, si può definire la misura del segmento orientato Z1Z2, come la differenza delle ascisse z1 e z2 rispetto al sistema coordinato assegnato, cioè
Z1Z2 = z2 - z1.
Definizione 2
Considerati Z1, Z2 punti dell'estensione complessa, essi si dicono complessi e coniugati se le loro ascisse sono numeri complessi e coniugati in un sistema coordinato qualsiasi.
Si dimostra che due punti, che hanno per ascisse numeri complessi e coniugati, hanno per ascisse numeri complessi e coniugati in un sistema coordinato qualsiasi.
Ciò prova anche che
Infatti, considerati i numeri complessi e coniugati x + iy ed x - iy, essendo in generale che
in cui z è un numero complesso, si ha che:
il trasformato del primo numero complesso è z' = α(x + iy) + β = αx + β + iαy,
il trasformato del secondo numero complesso è z'' = α(x - iy) + β = αx + β - iαy,
e ciò dimostra che anche i trasformati sono numeri complessi e coniugati.
Definizione 3
Considerata una terna ordinata di numeri complessi Z1, Z2, Z3, Z2 ≠ Z3, si chiama rapporto semplice il numero definito da
dove z1, z2, z3 sono le ascisse in un determinato sistema coordinato, ed anche se il riferimento
Punto medio tra due punti dell'estensione complessa
Z3 è punto medio tra Z1 e Z2, se il rapporto semplice della terna ordinata Z1, Z2, Z3 è uguale a -1, cioè
(Z1 Z2 Z3) = -1.
Si può quindi dedurre l'ascissa del punto medio di un'estensione complessa con dimostrazione analoga a quella della retta reale.
Il punto medio fra due punti complessi e coniugati è un numero reale.
Infatti, sia Z un punto complesso, in un sistema coordinato qualsiasi che abbia ascissa x + iy, e Z' un altro punto complesso, di ascissa x - iy. L'ascissa del punto medio, indicata con M(X) è data dalla semisomma delle due, cioè:
Gruppo di trasformazioni
Si supponga che E sia un insieme di elementi e Φ un insieme di trasformazioni di E in E, ossia
a)
b)
Si deduce subito che a Φ appartiene la trasformazione identica, che ad ogni elemento di E fa corrispondere lo stesso elemento.
Infatti, considerato f
f-1ο f
mentre per la b)
f-1
Si vuole vedere ora come si definisce f-1ο f e, allo scopo, si costruisce il seguente diagramma:
quindi
f-1ο f = i, f ο f-1 = i
e risulta
f ο i = i ο f,
cioè i funziona da elemento neutro.
Si dimostra ora che l'insieme di tutte le trasformazioni lineari intere sull'insieme dei reali è un gruppo di trasformazioni e, similmente, l'insieme di tutte le estensioni complesse delle trasformazioni lineari intere è un gruppo di trasformazioni.
f
Per dimostrare che l'insieme di tutte le trasformazioni lineari intere sull'insieme dei reali è un gruppo di trasformazioni, occorre dimostrare che:
1) il prodotto di due trasformazioni lineari intere è una trasformazione lineare intera.
2) l'inversa di una trasformazione lineare intera è una trasformazione lineare intera.
Dimostrazione 1)
Si considerino due trasformazioni lineari intere:
con
α
e
con
α'
Si deve dimostrare che il prodotto T'T, o la componente delle due trasformazioni, è una trasformazione lineare intera.
Se x è il generico numero reale, ad esso si fa corrispondere mediante T il numero reale αx + β, quindi
Si consideri ora il trasformato di αx + β mediante T', che è dato da αx + β + β', quindi
Pertanto, T'T trasforma il generico x, come segue:
Si pongono ora
α'α = α'', α'β + β' = β'',
con α'' R, β''
R, β'' R, α'' ≠ 0
R, α'' ≠ 0
e, sostituendo nella relazione suddetta, si ha:
con
α''
E' quindi dimostrato che il il prodotto di due trasformazioni lineari intere è una trasformazione lineare intera, cioè questa è la prima proprietà che soddisfa un gruppo di trasformazioni.
Dimostrazione 2)
Si consideri una generica trasformazione lineare intera:
con
α
Si fissi un elemento y per poter trovare l'y' che ha come corrispondente y nella trasformazione T, quindi si ha
y = αy' + β,
da cui
pertanto risulta
e quindi si può dire che il generico x è trasformato dall'inverso di T in
Indicando a tal punto
si ottiene che la trasformazione inversa è dello stesso tipo della trasformazione lineare intera, quindi
con
α'
E' quindi dimostrato anche che l'inversa di una trasformazione lineare intera è una trasformazione lineare intera, e quindi l'insieme di tutte le trasformazioni lineari intere sull'insieme dei reali è un gruppo di trasformazioni, anche quando si considera l'insieme di tutte le estensioni complesse delle trasformazioni lineari intere, ferme restanti le condizioni
α