CIRCONFERENZA ---> INDICE
Fissati un riferimento metrico
ed un punto C(α, β), si definisce circonferenza il luogo geometrico dei punti del piano che
distano dal punto C, detto centro, di una distanza r assegnata, detta raggio.
Si ricava ora l'equazione della circonferenza dalla sua definizione geometrica.
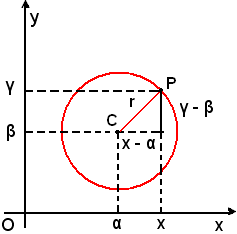
Sia C(α, β) il centro della circonferenza ed r il suo raggio; se P di coordinate x ed y è un suo punto, risulta:
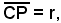
ossia, applicando la formula della distanza del punto C dal punto P, si ha
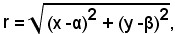
da cui, elevando al quadrato ambo i membri, si ottiene
(1) r2 = (x - α)2 + (y - β)2.
Sviluppando e ordinando, la (1) diventa
(2) x2 + y2 - 2αx - 2βy + γ = 0,
in cui si è posto:
γ = α2 + β2 - r2,
quindi
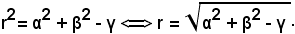
La (2) è soddisfatta dalle coordinate di tutti i punti della circonferenza; viceversa, se le coordinate di un punto del piano soddisfano la (2), il punto ha distanza r dal centro, e perciò appartiene al cerchio. Si può dunque dire che l'equazione (2) rappresenta l'equazione del cerchio di centro C(α, β) e di raggio r.
Se si considera il centro C di coordinate α= -a/2, β = -b/2, ed inoltre γ = c, sostituendo tali valori nella (2), si ha
x2 + y2 + ax + by + c = 0,
inoltre
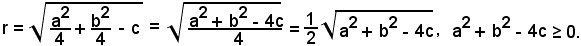
Si osserva ora che:
a) se a2 + b2 - 4c ≥ 0, la circonferenza ha infiniti punti reali;
b) se a2 + b2 - 4c = 0, la circonferenza ha il raggio nullo e si spezza in due rette complesse e
coniugate, quindi ha un solo punto reale;
c) se a2 + b2 - 4c < 0, la circonferenza ha il raggio immaginario e punti non reali, con a, b, c reali. Se invece a, b, c sono complessi, la circonferenza è complessa.
Esempio
Si consideri la circonferenza complessa di equazione
x2 + y2 - 2iy - 1 = 0;
essa ha al massimo due punti reali: (1, 0), (-1, 0).
Si osserva che se A, B, C sono tre punti reali, la circonferenza che passa per questi tre punti ha infiniti punti reali, pertanto essa è reale.
Dopo tali considerazioni, si considerano le circonferenze che hanno infiniti punti reali e l'insieme dei punti interni alla circonferenza (cerchio), si vede quindi la condizione necessaria e sufficiente affinchè un punto P0(x0, y0) sia interno o esterno alla circonferenza.
Punti interni ed esterni alla circonferenza
Sia C(α, β) il centro della circonferenza ed r il raggio, r > 0. Quindi, se il punto è interno alla circonferenza, siccome l'equazione della circonferenza è
(x - α)2 + (y - β)2 = r2,
essa diventa
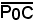2 < r2 
(x0 - α)2 + (y0 - β)2 < r2 x02 + y02 - 2αx0 - 2βy0 + α2 + β2 - r2 < 0.
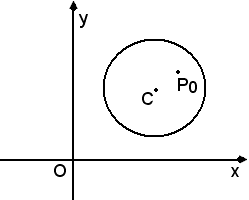
Ciò esprime che, se sono noti r, x0, y0, α, β, si ottiene un numero minore di zero.
Quindi, se si ha un numero minore di zero, il punto P0 è interno alla circonferenza.
Se invece il punto P0 è esterno alla circonferenza, si ha un numero maggiore di zero, osservando che, come prima, risulta:
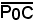2 > r2 (x0 - α)2 + (y0 - β)2 > r2 x02 + y02 - 2αx0 - 2βy0 + α2 + β2 - r2 > 0.
Si considera ora l'equazione
l(x2 + y2) + mx + ny + p = 0,
con l ≠ 0, di una circonferenza a punti reali.
Si vuole stabilire una condizione affinchè un punto sia interno o esterno alla circonferenza:
se l è positivo, ciò si può stabilire, se è negativo si possono stabilire i casi contrari.
Essendo l ≠ 0, si può moltiplicare l'equazione per 1/l, ottenendo così
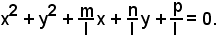
Siccome la circonferenza è supposta reale, i rapporti m/l, n/l, p/l sono reali, quindi si può ricorrere alla formula generale e, come è stato già visto, la condizione se un punto è esterno o interno è nota.
Si osserva ora che, se si ha una circonferenza di raggio nullo, essa ha un solo punto reale e gli altri punti del piano sono esterni alla circonferenza, quindi la sua equazione è:
(x - α)2 + (y - β)2 = 0,
inoltre, se P0 ≠ C,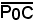2 > 0.
Se la circonferenza non ha punti reali, il raggio è un numero immaginario r = ia, con a > 0, quindi l'equazione della circonferenza è:
(x - α)2 + (y - β)2 = -a2,
inoltre,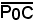2 > -a2.
Equazioni parametriche di una circonferenza
Si considera ora una circonferenza di raggio r e centro C(α, β) di equazione
(x - α)2 + (y - β)2 = r2
e si divide tale equazione per r2, si ottiene quindi:
Si prende ora
0 ≤ θ < 2π
e si osserva che
cos2θ + sen2θ = 1,
ed inoltre che se x ed y sono soluzioni dell'equazione, essi devono essere tali che
Quindi, al variare di θ si ottengono coppie ordinate di numeri che sono punti della circonferenza, cioè
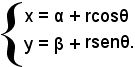
con θ parametro, rappresenta un sistema di equazioni parametriche della circonferenza di raggio r e centro C(α, β), con 0 ≤ θ < 2π.
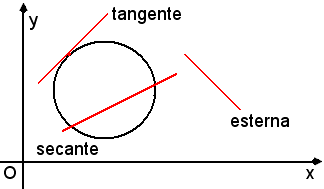
Rette tangenti, secanti ed esterne ad una circonferenza
Si consideri una circonferenza che ha infiniti punti reali e siano A, B, C tre di essi, la sua equazione, come è noto, è
1) x2 + y2 + ax + by + c = 0,
inoltre
a2 + b2 - 4c ≥ 0.
Si consideri ora l'equazione di una retta:
2) ux + vy + w = 0,
-se la retta è tangente alla circonferenza, essa ha in comune un solo punto;
-se la retta è secante, essa ha in comune due punti;
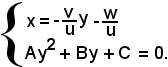
Si osserva ora che l'equazione di secondo grado di tale sistema può ammettere:
-due radici reali e distinte se Δ > 0,
-due radici reali e coincidenti se Δ = 0,
-due radici complesse e coniugate se Δ < 0.
Se Δ > 0, siano y1 ed y2 le due radici reali e distinte, quindi in loro corrispondenza, sostituendo nell'equazione di primo grado, si hanno i valori di x1 ed x2. Pertanto, si hanno due soluzioni reali e distinte rappresentate dalle coppie (x1, y1), (x2, y2) e quindi due punti in comune fra retta e circonferenza. In tal caso, la retta risulta secante alla circonferenza.
Se Δ = 0, siano y1 ed y2 le due radici reali e coincidenti, cioè y1 = y2, quindi in loro corrispondenza, sostituendo nell'equazione di primo grado, si ha x1 = x2. Pertanto, si hanno due soluzioni reali e coincidenti rappresentate dalle coppie (x1, y1) = (x2, y2) e quindi un punto in comune fra retta e circonferenza. In tal caso, la retta risulta tangente alla circonferenza.
Se Δ < 0, siano y1 ed y2 le due radici complesse e coniugate, quindi si hanno due punti complessi e coniugati. In tal caso, la retta risulta esterna alla circonferenza.
Concludendo, si può dire che:
-se la retta è secante, essa ha in comune con la circonferenza due punti reali e distinti;
-se la retta è tangente, essa ha in comune con la circonferenza due punti reali e coincidenti;
-se la retta è esterna, essa e la circonferenza forniscono punti complessi e coniugati.
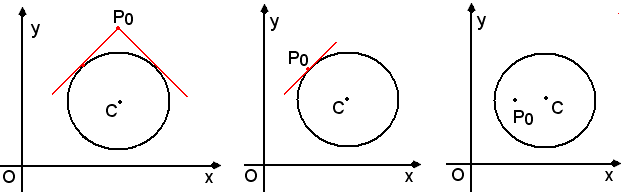
Si considerino ora una circonferenza ed un punto P0:
-se P0 è esterno alla circonferenza, si hanno due tangenti;
-se P0 appartiene alla circonferenza, si ha una tangente;
-se P0 è interno alla circonferenza, si hanno due tangenti complesse e coniugate.
E' noto che una generica retta per P0 ha equazione del tipo
y - y0 = m(x - x0),
con m parametro non omogeneo o del tipo
a(x - x0) + b(y - y0),
con a, b parametri omogenei.
Per determinare la distanza del punto dalla circonferenza, basta imporre che la distanza della retta passante per P0 e per il centro sia uguale al raggio r, cioè
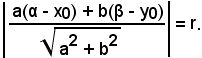
Se P0 appartiene alla circonferenza, basta considerare la retta CP0 e la tangente non è altro che la perpendicolare alla retta.
Si dimostra che, se P0(x0, y0) appartiene alla circonferenza, l'equazione della tangente è
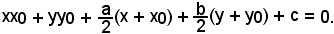
Circonferenza passante per tre punti
Siano assegnati i punti P1(x1, y1), P2(x2, y2), P3(x3, y3), tali che
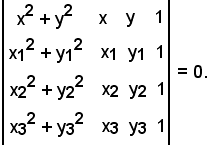
Questa è l'equazione di una circonferenza passante per tre punti assegnati.
Ciò è vero in quanto, per provare che la circonferenza passa per P1, basta sostituire le coordinate di tale punto nella prima equazione, quindi il determinante viene ad avere le prime due righe uguali, pertanto è uguale a zero. Analogo ragionamento si fa per gli altri punti.
Fascio di circonferenze
Si considerano due circonferenze
C1) x2 + y2 + ax + by + c = 0,
C2) x2 + y2 + a'x + b'y + c' = 0,
C1 ≠ C2,
e la seguente combinazione lineare di C1) e C2):
(λ + μ)(x2 + y2) + (λa + μa')x + (λb + μb')y + λc + μc' = 0,
con (λ, μ) ≠ (0, 0), λ + μ ≠ 0.
In tal modo, si è ottenuta un'altra circonferenza di equazione suddetta.
Se un punto P0(x0, y0) è comune a C1) e C2), esso appartiene ad ogni circonferenza del fascio, quindi soddisfa le equazioni di C1) e C2).
Si osserva ora che, se le due circonferenze non hanno alcun punto in comune, esse sono concentriche, inoltre se C1) e C2) hanno lo stesso centro, il fascio di circonferenze individuato ha il centro nel centro del fascio.
Si osserva ancora che, se una circonferenza passa per due punti, essa appartiene al fascio, e questi due punti si chiamano punti base.
Ciò osservato, si ritorna all'equazione
(λ + μ)(x2 + y2) + (λa + μa')x + (λb + μb')y + λc + μc' = 0
e si fanno le seguenti considerazioni:
λ + μ = 0, λa + μa' = 0, λb + μb' = 0, λc + μc' ≠ 0
a = a', b = b', c ≠ c',
pertanto le circonferenze risultano concentriche.
Si dimostra ora che tutte le circonferenze del fascio hanno lo stesso centro.
Infatti, si sostituisce nell'equazione suddetta a al posto di a' e b al posto di b', ottenendo:
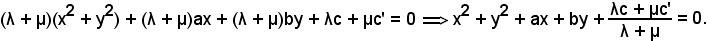
Si esamina il caso in cui (a, b) ≠ (a', b'), cioè che non si verifichi contemporaneamente a = a', b = b', e ciò significa che le due circonferenze non sono concentriche, quindi operando allo stesso modo di prima si ha:
(λa - λa')x + (λb - λb')y + λc - λc' = 0 (a - a')x + (b - b')y + c - c' = 0. (*)
Si osserva che (*) si è ottenuta sottraendo membro a membro le equazioni di C1) e C2).Quest'ultima
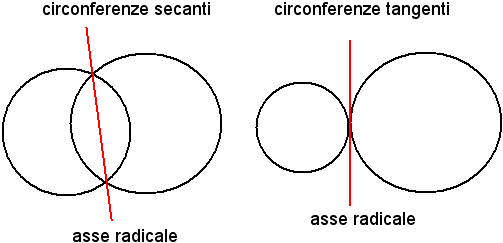
è l'equazione di una retta che prende il nome di asse radicale e passa
per i punti base del fascio.
Per determinare i punti base del fascio, bisogna trovare le soluzioni del sistema formato dalle equazioni di C1) e C2), oppure dal sistema formato da C1) ed (*), o ancora da quello formato da C2) ed (*). Pertanto, se si hanno soluzioni reali distinte, si hanno circonferenze secanti; se si hanno soluzioni reali coincidenti, si hanno circonferenze tangenti; se si hanno soluzioni complesse e coniugate, si hanno circonferenze complesse e coniugate.
Si ha quindi
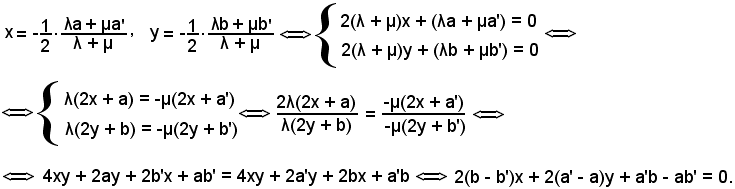
Quest'ultima è l'equazione di una retta, perchè i coefficienti non sono tutti nulli, e prende il nome di asse centrale, che è perpendicolare all'asse radicale.
Potenza di un punto rispetto alla circonferenza
Si ricava ora l'equazione della circonferenza dalla sua definizione geometrica.
Sia C(α, β) il centro della circonferenza ed r il suo raggio; se P di coordinate x ed y è un suo punto, risulta:
ossia, applicando la formula della distanza del punto C dal punto P, si ha
da cui, elevando al quadrato ambo i membri, si ottiene
(1) r2 = (x - α)2 + (y - β)2.
Sviluppando e ordinando, la (1) diventa
(2) x2 + y2 - 2αx - 2βy + γ = 0,
in cui si è posto:
γ = α2 + β2 - r2,
quindi
La (2) è soddisfatta dalle coordinate di tutti i punti della circonferenza; viceversa, se le coordinate di un punto del piano soddisfano la (2), il punto ha distanza r dal centro, e perciò appartiene al cerchio. Si può dunque dire che l'equazione (2) rappresenta l'equazione del cerchio di centro C(α, β) e di raggio r.
Se si considera il centro C di coordinate α= -a/2, β = -b/2, ed inoltre γ = c, sostituendo tali valori nella (2), si ha
x2 + y2 + ax + by + c = 0,
inoltre
Si osserva ora che:
a) se a2 + b2 - 4c ≥ 0, la circonferenza ha infiniti punti reali;
b) se a2 + b2 - 4c = 0, la circonferenza ha il raggio nullo e si spezza in due rette complesse e
coniugate, quindi ha un solo punto reale;
c) se a2 + b2 - 4c < 0, la circonferenza ha il raggio immaginario e punti non reali, con a, b, c reali. Se invece a, b, c sono complessi, la circonferenza è complessa.
Esempio
Si consideri la circonferenza complessa di equazione
x2 + y2 - 2iy - 1 = 0;
essa ha al massimo due punti reali: (1, 0), (-1, 0).
Si osserva che se A, B, C sono tre punti reali, la circonferenza che passa per questi tre punti ha infiniti punti reali, pertanto essa è reale.
Dopo tali considerazioni, si considerano le circonferenze che hanno infiniti punti reali e l'insieme dei punti interni alla circonferenza (cerchio), si vede quindi la condizione necessaria e sufficiente affinchè un punto P0(x0, y0) sia interno o esterno alla circonferenza.
Punti interni ed esterni alla circonferenza
Sia C(α, β) il centro della circonferenza ed r il raggio, r > 0. Quindi, se il punto è interno alla circonferenza, siccome l'equazione della circonferenza è
(x - α)2 + (y - β)2 = r2,
essa diventa
2 < r2 (x0 - α)2 + (y0 - β)2 < r2 x02 + y02 - 2αx0 - 2βy0 + α2 + β2 - r2 < 0.Ciò esprime che, se sono noti r, x0, y0, α, β, si ottiene un numero minore di zero.
Quindi, se si ha un numero minore di zero, il punto P0 è interno alla circonferenza.
Se invece il punto P0 è esterno alla circonferenza, si ha un numero maggiore di zero, osservando che, come prima, risulta:
2 > r2 (x0 - α)2 + (y0 - β)2 > r2 x02 + y02 - 2αx0 - 2βy0 + α2 + β2 - r2 > 0.Si considera ora l'equazione
l(x2 + y2) + mx + ny + p = 0,
con l ≠ 0, di una circonferenza a punti reali.
Si vuole stabilire una condizione affinchè un punto sia interno o esterno alla circonferenza:
se l è positivo, ciò si può stabilire, se è negativo si possono stabilire i casi contrari.
Essendo l ≠ 0, si può moltiplicare l'equazione per 1/l, ottenendo così
Siccome la circonferenza è supposta reale, i rapporti m/l, n/l, p/l sono reali, quindi si può ricorrere alla formula generale e, come è stato già visto, la condizione se un punto è esterno o interno è nota.
Si osserva ora che, se si ha una circonferenza di raggio nullo, essa ha un solo punto reale e gli altri punti del piano sono esterni alla circonferenza, quindi la sua equazione è:
(x - α)2 + (y - β)2 = 0,
inoltre, se P0 ≠ C,
2 > 0.Se la circonferenza non ha punti reali, il raggio è un numero immaginario r = ia, con a > 0, quindi l'equazione della circonferenza è:
(x - α)2 + (y - β)2 = -a2,
inoltre,
2 > -a2.Equazioni parametriche di una circonferenza
Si considera ora una circonferenza di raggio r e centro C(α, β) di equazione
(x - α)2 + (y - β)2 = r2
e si divide tale equazione per r2, si ottiene quindi:
Si prende ora
0 ≤ θ < 2π
e si osserva che
cos2θ + sen2θ = 1,
ed inoltre che se x ed y sono soluzioni dell'equazione, essi devono essere tali che
Quindi, al variare di θ si ottengono coppie ordinate di numeri che sono punti della circonferenza, cioè
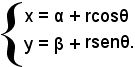
con θ parametro, rappresenta un sistema di equazioni parametriche della circonferenza di raggio r e centro C(α, β), con 0 ≤ θ < 2π.
Rette tangenti, secanti ed esterne ad una circonferenza
Si consideri una circonferenza che ha infiniti punti reali e siano A, B, C tre di essi, la sua equazione, come è noto, è
1) x2 + y2 + ax + by + c = 0,
inoltre
a2 + b2 - 4c ≥ 0.
Si consideri ora l'equazione di una retta:
2) ux + vy + w = 0,
-se la retta è tangente alla circonferenza, essa ha in comune un solo punto;
-se la retta è secante, essa ha in comune due punti;
-se la retta è esterna alla circonferenza, essa non ha alcun punto in comune.
Si osserva che se la retta e la circonferenza hanno in comune due punti, le due equazioni devono avere soluzioni in comune e, supposto
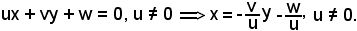
Sostituendo tale valore in 1), e facendo opportune posizioni, cioè ponendo uguale ad A il coefficiente della x ed uguale a B il coefficiente della y, si ha:
Ay2 + By + C = 0, A ≠ 0.
Ci si trova quindi di fronte al sistema
Si osserva che se la retta e la circonferenza hanno in comune due punti, le due equazioni devono avere soluzioni in comune e, supposto
Sostituendo tale valore in 1), e facendo opportune posizioni, cioè ponendo uguale ad A il coefficiente della x ed uguale a B il coefficiente della y, si ha:
Ay2 + By + C = 0, A ≠ 0.
Ci si trova quindi di fronte al sistema
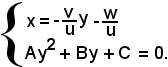
Si osserva ora che l'equazione di secondo grado di tale sistema può ammettere:
-due radici reali e distinte se Δ > 0,
-due radici reali e coincidenti se Δ = 0,
-due radici complesse e coniugate se Δ < 0.
Se Δ > 0, siano y1 ed y2 le due radici reali e distinte, quindi in loro corrispondenza, sostituendo nell'equazione di primo grado, si hanno i valori di x1 ed x2. Pertanto, si hanno due soluzioni reali e distinte rappresentate dalle coppie (x1, y1), (x2, y2) e quindi due punti in comune fra retta e circonferenza. In tal caso, la retta risulta secante alla circonferenza.
Se Δ = 0, siano y1 ed y2 le due radici reali e coincidenti, cioè y1 = y2, quindi in loro corrispondenza, sostituendo nell'equazione di primo grado, si ha x1 = x2. Pertanto, si hanno due soluzioni reali e coincidenti rappresentate dalle coppie (x1, y1) = (x2, y2) e quindi un punto in comune fra retta e circonferenza. In tal caso, la retta risulta tangente alla circonferenza.
Se Δ < 0, siano y1 ed y2 le due radici complesse e coniugate, quindi si hanno due punti complessi e coniugati. In tal caso, la retta risulta esterna alla circonferenza.
Concludendo, si può dire che:
-se la retta è secante, essa ha in comune con la circonferenza due punti reali e distinti;
-se la retta è tangente, essa ha in comune con la circonferenza due punti reali e coincidenti;
-se la retta è esterna, essa e la circonferenza forniscono punti complessi e coniugati.
Si considerino ora una circonferenza ed un punto P0:
-se P0 è esterno alla circonferenza, si hanno due tangenti;
-se P0 appartiene alla circonferenza, si ha una tangente;
-se P0 è interno alla circonferenza, si hanno due tangenti complesse e coniugate.
E' noto che una generica retta per P0 ha equazione del tipo
y - y0 = m(x - x0),
con m parametro non omogeneo o del tipo
a(x - x0) + b(y - y0),
con a, b parametri omogenei.
Per determinare la distanza del punto dalla circonferenza, basta imporre che la distanza della retta passante per P0 e per il centro sia uguale al raggio r, cioè
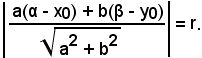
Se P0 appartiene alla circonferenza, basta considerare la retta CP0 e la tangente non è altro che la perpendicolare alla retta.
Si dimostra che, se P0(x0, y0) appartiene alla circonferenza, l'equazione della tangente è
Circonferenza passante per tre punti
Siano assegnati i punti P1(x1, y1), P2(x2, y2), P3(x3, y3), tali che
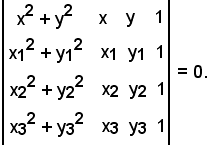
Questa è l'equazione di una circonferenza passante per tre punti assegnati.
Ciò è vero in quanto, per provare che la circonferenza passa per P1, basta sostituire le coordinate di tale punto nella prima equazione, quindi il determinante viene ad avere le prime due righe uguali, pertanto è uguale a zero. Analogo ragionamento si fa per gli altri punti.
Fascio di circonferenze
Si considerano due circonferenze
C1) x2 + y2 + ax + by + c = 0,
C2) x2 + y2 + a'x + b'y + c' = 0,
C1 ≠ C2,
e la seguente combinazione lineare di C1) e C2):
(λ + μ)(x2 + y2) + (λa + μa')x + (λb + μb')y + λc + μc' = 0,
con (λ, μ) ≠ (0, 0), λ + μ ≠ 0.
In tal modo, si è ottenuta un'altra circonferenza di equazione suddetta.
Se un punto P0(x0, y0) è comune a C1) e C2), esso appartiene ad ogni circonferenza del fascio, quindi soddisfa le equazioni di C1) e C2).
Si osserva ora che, se le due circonferenze non hanno alcun punto in comune, esse sono concentriche, inoltre se C1) e C2) hanno lo stesso centro, il fascio di circonferenze individuato ha il centro nel centro del fascio.
Si osserva ancora che, se una circonferenza passa per due punti, essa appartiene al fascio, e questi due punti si chiamano punti base.
Ciò osservato, si ritorna all'equazione
(λ + μ)(x2 + y2) + (λa + μa')x + (λb + μb')y + λc + μc' = 0
e si fanno le seguenti considerazioni:
λ + μ = 0, λa + μa' = 0, λb + μb' = 0, λc + μc' ≠ 0
a = a', b = b', c ≠ c',pertanto le circonferenze risultano concentriche.
Si dimostra ora che tutte le circonferenze del fascio hanno lo stesso centro.
Infatti, si sostituisce nell'equazione suddetta a al posto di a' e b al posto di b', ottenendo:
Si esamina il caso in cui (a, b) ≠ (a', b'), cioè che non si verifichi contemporaneamente a = a', b = b', e ciò significa che le due circonferenze non sono concentriche, quindi operando allo stesso modo di prima si ha:
(λa - λa')x + (λb - λb')y + λc - λc' = 0
(a - a')x + (b - b')y + c - c' = 0. (*)Si osserva che (*) si è ottenuta sottraendo membro a membro le equazioni di C1) e C2).
Per determinare i punti base del fascio, bisogna trovare le soluzioni del sistema formato dalle equazioni di C1) e C2), oppure dal sistema formato da C1) ed (*), o ancora da quello formato da C2) ed (*). Pertanto, se si hanno soluzioni reali distinte, si hanno circonferenze secanti; se si hanno soluzioni reali coincidenti, si hanno circonferenze tangenti; se si hanno soluzioni complesse e coniugate, si hanno circonferenze complesse e coniugate.
Si ha quindi
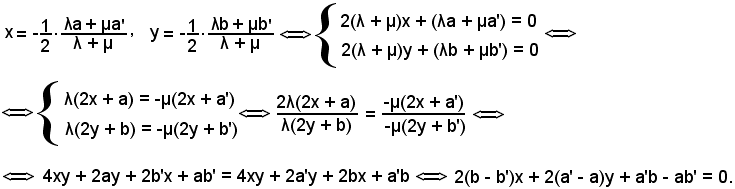
Quest'ultima è l'equazione di una retta, perchè i coefficienti non sono tutti nulli, e prende il nome di asse centrale, che è perpendicolare all'asse radicale.
Potenza di un punto rispetto alla circonferenza
Considerata una circonferenza, si definisce potenza p di un punto P0 rispetto alla circonferenza il prodotto della misura dei segmenti orientati da P0 agli estremi del diametro appartenente alla retta CP0, cioè
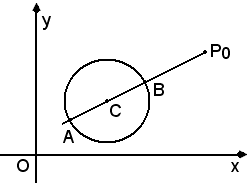
Considerato il raggio r della circonferenza, si vede subito che la potenza p del punto P0 è:
Tenendo conto che
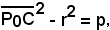
-se il punto P0 è esterno alla circonferenza, p > 0;
-se il punto P0 è interno alla circonferenza, p < 0.
Si dimostra che l'asse radicale, di circonferenze non concentriche, è il luogo dei punti del piano che hanno la stessa potenza rispetto alle circonferenze del fascio.
Infatti, si considerano le equazioni delle due circonferenze
C1) x2 + y2 + ax + by + c = 0,
C2) x2 + y2 + a'x + b'y + c' = 0,
e l'equazione del fascio, che come è noto è
(λ + μ)(x2 + y2) + (λa + μa')x + (λb + μb')y + λc + μc' = 0.
Si dimostra che, se un punto P0(x0, y0) ha la stessa potenza rispetto alla circonferenza del fascio, in particolare avrà la stessa potenza rispetto alle due circonferenze che individuano il fascio, cioè
x02 + y02 + ax0 + by0 + c = x02 + y02 + a'x0 + b'y0 + c' (a - a')x0 + (b - b')y0 + c - c' = 0.
Quindi, se un punto ha la stessa potenza rispetto a tutte le circonferenze, esso appartiene all'asse radicale.
Viceversa, dire che un punto appartiene all'asse radicale, cioè che sia
(a - a')x0 + (b - b')y0 + c - c' = 0 ax0 + by0 + c = a'x0 + b'y0 + c'.
Si determina ora la potenza di un punto rispetto ad una generica equazione del fascio.
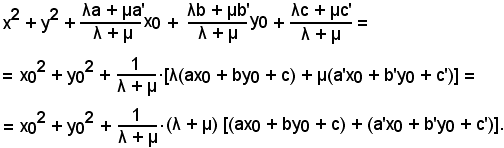
Quindi, se il numero è individuato da (λ, μ), la potenza è la stessa.
Esempi
Considerato il raggio r della circonferenza, si vede subito che la potenza p del punto P0 è:
Tenendo conto che
-se il punto P0 è esterno alla circonferenza, p > 0;
-se il punto P0 è interno alla circonferenza, p < 0.
Si dimostra che l'asse radicale, di circonferenze non concentriche, è il luogo dei punti del piano che hanno la stessa potenza rispetto alle circonferenze del fascio.
Infatti, si considerano le equazioni delle due circonferenze
C1) x2 + y2 + ax + by + c = 0,
C2) x2 + y2 + a'x + b'y + c' = 0,
e l'equazione del fascio, che come è noto è
(λ + μ)(x2 + y2) + (λa + μa')x + (λb + μb')y + λc + μc' = 0.
Si dimostra che, se un punto P0(x0, y0) ha la stessa potenza rispetto alla circonferenza del fascio, in particolare avrà la stessa potenza rispetto alle due circonferenze che individuano il fascio, cioè
x02 + y02 + ax0 + by0 + c = x02 + y02 + a'x0 + b'y0 + c'
(a - a')x0 + (b - b')y0 + c - c' = 0.Quindi, se un punto ha la stessa potenza rispetto a tutte le circonferenze, esso appartiene all'asse radicale.
Viceversa, dire che un punto appartiene all'asse radicale, cioè che sia
(a - a')x0 + (b - b')y0 + c - c' = 0
ax0 + by0 + c = a'x0 + b'y0 + c'.Si determina ora la potenza di un punto rispetto ad una generica equazione del fascio.
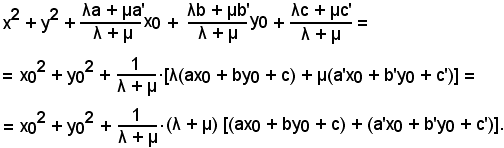
Quindi, se il numero è individuato da (λ, μ), la potenza è la stessa.
Esempi
1)-Data la circonferenza
C) x2 + y2 - 2x + 3 = 0,
determinare la distanza d dal centro alla retta
r) x + y - 1 = 0
e le intersezioni di questa con la circonferenza.
Le coordinate del centro C(α, β) sono date da α = -a/2 = -2/-2 = 1 e β = -b/2 = 0/2 = 0, quindi C(1, 0); inoltre
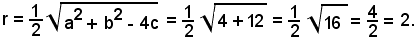
La distanza d dal centro alla retta è data da
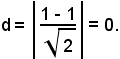
Quindi, la retta r passa per il centro della circonferenza.
Le intersezioni della retta r con la circonferenza sono reali e si trovano risolvendo il sistema formato dalle equazioni della retta r e della circonferenza:
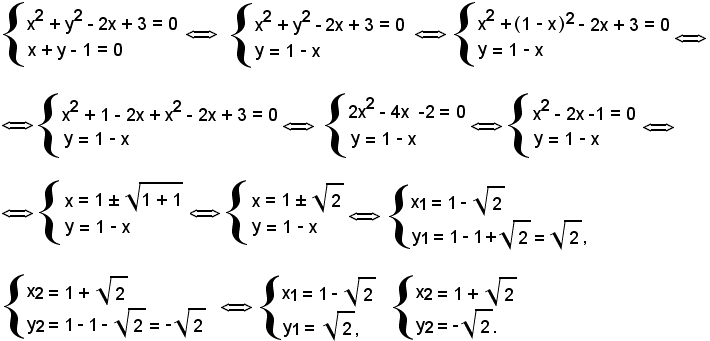
2)-Dell'equazione della retta
x + y - λ = 0,
determinare λ in modo che la retta sia tangente alla circonferenza di equazione
x2 + y2 - 2x + 3 = 0.
Si osserva che nell'esercizio 1) si è trovato che il centro della circonferenza è C(1, 0), inoltre r = 2. Ora si considera il sistema formato dalle equazioni della retta r e della circonferenza:
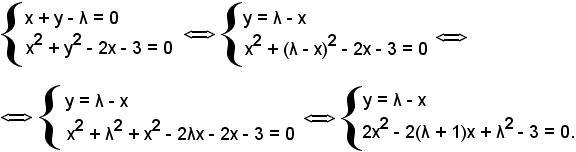
Affinchè la retta sia tangente alla circonferenza, il delta dell'equazione di secondo grado dev'essere uguale a zero:
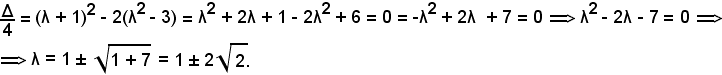
Quindi, in corrispondenza di tali valori di λ si ottengono le equazioni delle due tangenti alla circonferenza:
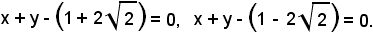
3)-Determinare le tangenti dal punto A(1, 3) alla circonferenza di equazione
x2 + y2 + 4x + 2y - 4 = 0.
Il centro risulta C(-2, -1), mentre il raggio r è dato da:
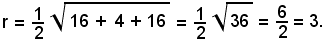
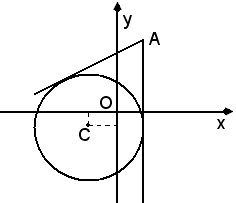
Si considera ora l'equazione del fascio di rette passante per il punto A, e quindi il sistema formato da questa equazione con quella della circonferenza:
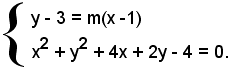
Siccome y = 3 + mx - m, sostituendo tale valore nella seconda equazione, si ha:
x2 + 9 + m2 + m2x2 - 6m + 6mx - 2m2x + 4x + 6 + 2mx - 2m - 4 = 0 (1 + m2)x2 -
- 2(m2 - 4m - 2)x + m2 - 8m + 11 = 0.
Affinchè la retta sia tangente alla circonferenza, il delta dell'equazione dev'essere uguale a zero:
Quindi, in corrispondenza di tale valore di m, si ottiene una delle due equazioni delle tangenti alla circonferenza, cioè
7x - 24y + 65 = 0;
l'altra equazione è data dalla retta ottenuta considerando m = ∞, che è:
x - 1 = 0.
4)-Determinare l'equazione della circonferenza passante per l'origine ed avente centro C(1, 1).
Per determinare l'equazione della circonferenza, si ricorre alla formula
r2 = (x - α)2 + (y - β)2,
in cui α = 1 e β = 1 rappresentano le coordinate del centro C.
Ora, si calcola il raggio r, espresso da
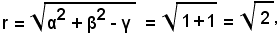
in cui γ = 0, perchè la circonferenza passa per l'origine.
Dunque, si ha:
r2 = (x - α)2 + (y - β)2 2 = (x - 1)2 + (y - 1)2 x2 - 2x + 1 + y2 - 2y + 1 - 2 = 0
x2 + y2 - 2x - 2y = 0.
5)-Determinare λ in modo che la circonferenza di equazione
x2 + y2 - 2λx + 2y - 1 = 0
stacchi sull'asse x un segmento 2h ≥ 0.
L'equazione in questione rappresenta l'equazione di un fascio di circonferenze non concentriche, quindi s'interseca la circonferenza con l'asse x, ottenendo
x2 - 2λx - 1 = 0.
Risolvendo tale equazione, si ha:
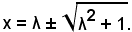
Pertanto, si ottengono i punti
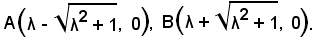
Quindi, il segmento
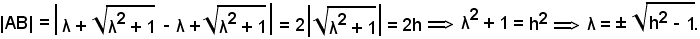
Siccome
h2 - 1 ≥ 0 h ≥ 1,
se
h = 1 λ = 0,
quindi
A(0, -1), B(0, 1).
6)-Determinare λ in modo che la circonferenza di equazione
x2 + y2 - 2x + 4y - λ = 0
sia tangente alla retta r di equazione
x - y = 0.
Infatti, per risolvere l'esercizio, si trova il centro C che ha coordinate (1, 2), e s'impone la condizione di tangenza della retta r con la circonferenza e facilmente si calcola λ.
7)-Determinare l'equazione della circonferenza tangente alla retta r di equazione
x + 2y - 1 = 0
nel punto A(3, -1) e passante per l'origine O.
Si considera l'equazione della circonferenza
x2 + y2 + ax + by + c = 0,
siccome essa passa per l'origine, risulta
c = 0,
siccome essa passa anche per A, risulta
9 +1 + 3a - b = 0,
cioè
b = 3a + 10,
infine, s'impone la condizione di tangenza, si ricavano i valori di a e b e poi si sostituiscono nell'equazione della circonferenza.
C) x2 + y2 - 2x + 3 = 0,
determinare la distanza d dal centro alla retta
r) x + y - 1 = 0
e le intersezioni di questa con la circonferenza.
Le coordinate del centro C(α, β) sono date da α = -a/2 = -2/-2 = 1 e β = -b/2 = 0/2 = 0, quindi C(1, 0); inoltre
La distanza d dal centro alla retta è data da
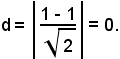
Quindi, la retta r passa per il centro della circonferenza.
Le intersezioni della retta r con la circonferenza sono reali e si trovano risolvendo il sistema formato dalle equazioni della retta r e della circonferenza:
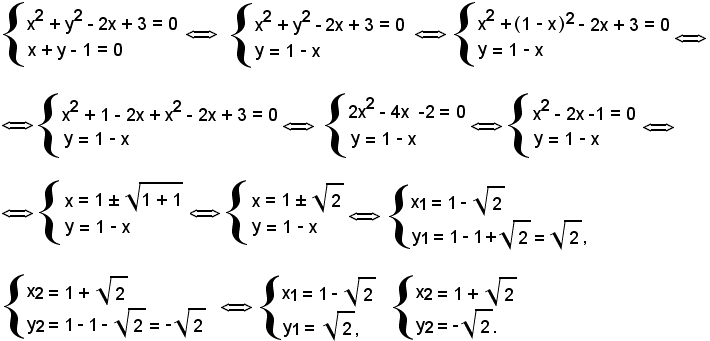
2)-Dell'equazione della retta
x + y - λ = 0,
determinare λ in modo che la retta sia tangente alla circonferenza di equazione
x2 + y2 - 2x + 3 = 0.
Si osserva che nell'esercizio 1) si è trovato che il centro della circonferenza è C(1, 0), inoltre r = 2. Ora si considera il sistema formato dalle equazioni della retta r e della circonferenza:
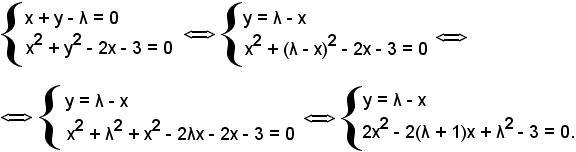
Affinchè la retta sia tangente alla circonferenza, il delta dell'equazione di secondo grado dev'essere uguale a zero:
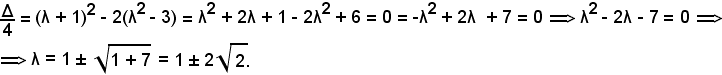
Quindi, in corrispondenza di tali valori di λ si ottengono le equazioni delle due tangenti alla circonferenza:
3)-Determinare le tangenti dal punto A(1, 3) alla circonferenza di equazione
x2 + y2 + 4x + 2y - 4 = 0.
Il centro risulta C(-2, -1), mentre il raggio r è dato da:
Si considera ora l'equazione del fascio di rette passante per il punto A, e quindi il sistema formato da questa equazione con quella della circonferenza:
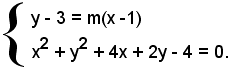
Siccome y = 3 + mx - m, sostituendo tale valore nella seconda equazione, si ha:
x2 + 9 + m2 + m2x2 - 6m + 6mx - 2m2x + 4x + 6 + 2mx - 2m - 4 = 0
(1 + m2)x2 -- 2(m2 - 4m - 2)x + m2 - 8m + 11 = 0.
Affinchè la retta sia tangente alla circonferenza, il delta dell'equazione dev'essere uguale a zero:
Δ/4 = (m2 - 4m - 2)2 - (1 + m2)(m2 - 8m + 11) = m4 + 16m2 + 4 - 8m3- 4m2 + 16m - m2 + 8m -
11 - m4 + 8m3- 11m2 = 24m - 7 = 0 m = 7/24.
m = 7/24.Quindi, in corrispondenza di tale valore di m, si ottiene una delle due equazioni delle tangenti alla circonferenza, cioè
7x - 24y + 65 = 0;
l'altra equazione è data dalla retta ottenuta considerando m = ∞, che è:
x - 1 = 0.
4)-Determinare l'equazione della circonferenza passante per l'origine ed avente centro C(1, 1).
Per determinare l'equazione della circonferenza, si ricorre alla formula
r2 = (x - α)2 + (y - β)2,
in cui α = 1 e β = 1 rappresentano le coordinate del centro C.
Ora, si calcola il raggio r, espresso da
in cui γ = 0, perchè la circonferenza passa per l'origine.
Dunque, si ha:
r2 = (x - α)2 + (y - β)2
2 = (x - 1)2 + (y - 1)2 x2 - 2x + 1 + y2 - 2y + 1 - 2 = 0 x2 + y2 - 2x - 2y = 0.5)-Determinare λ in modo che la circonferenza di equazione
x2 + y2 - 2λx + 2y - 1 = 0
stacchi sull'asse x un segmento 2h ≥ 0.
L'equazione in questione rappresenta l'equazione di un fascio di circonferenze non concentriche, quindi s'interseca la circonferenza con l'asse x, ottenendo
x2 - 2λx - 1 = 0.
Risolvendo tale equazione, si ha:
Pertanto, si ottengono i punti
Quindi, il segmento
Siccome
h2 - 1 ≥ 0
h ≥ 1,se
h = 1
λ = 0,quindi
A(0, -1), B(0, 1).
6)-Determinare λ in modo che la circonferenza di equazione
x2 + y2 - 2x + 4y - λ = 0
sia tangente alla retta r di equazione
x - y = 0.
Infatti, per risolvere l'esercizio, si trova il centro C che ha coordinate (1, 2), e s'impone la condizione di tangenza della retta r con la circonferenza e facilmente si calcola λ.
7)-Determinare l'equazione della circonferenza tangente alla retta r di equazione
x + 2y - 1 = 0
nel punto A(3, -1) e passante per l'origine O.
Si considera l'equazione della circonferenza
x2 + y2 + ax + by + c = 0,
siccome essa passa per l'origine, risulta
c = 0,
siccome essa passa anche per A, risulta
9 +1 + 3a - b = 0,
cioè
b = 3a + 10,
infine, s'impone la condizione di tangenza, si ricavano i valori di a e b e poi si sostituiscono nell'equazione della circonferenza.