ESTENSIONE COMPLESSA DI UN PIANO AFFINE ---> INDICE
Siano π un piano,
 (O, Ux, Uy) un riferimento ed f il sistema coordinato relativo ad
(O, Ux, Uy) un riferimento ed f il sistema coordinato relativo ad  ; siano inoltre
; siano inoltre
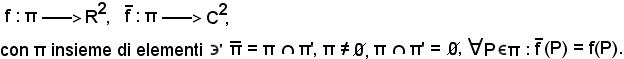
Si considera ora l'insieme (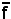 ) di tutte le bigezioni
) di tutte le bigezioni
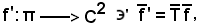
essendo la trasformazione affine reale C2.
la trasformazione affine reale C2.
Si chiama estensione complessa di π la coppia formata da da e dall'insieme (
e dall'insieme (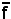 ), cioè
), cioè
( , (
, (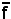 )).
)).
Gli elementi di quest'estensione complessa si chiamano punti complessi, mentre (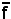 ) si chiama insieme dei sistemi coordinati di π.
) si chiama insieme dei sistemi coordinati di π.
Si osserva ora che:
P reale P
P π
π 
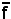 (P) = f(P)
(P) = f(P) R2
R2 
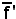 (P) =
(P) = 
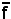 (P) =
(P) =  f(P)
f(P) R2.
R2.
Dunque, se P è reale, la coppia associata è sempre reale.
Siccome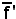 è bigezione, se P non appartiene a π, allora P
è bigezione, se P non appartiene a π, allora P π', quindi, quale che sia
π', quindi, quale che sia 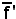 si ha che
si ha che 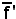 (P) non appartiene ad R2, cioè la coppia associata non è reale.
(P) non appartiene ad R2, cioè la coppia associata non è reale.
Definizione - Si dice che due punti P e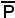 sono complessi e coniugati se e solo se le coppie
sono complessi e coniugati se e solo se le coppie
((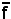 (P),
(P), 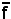 (
(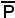 ))
))
sono coppie di numeri complessi e coniugati.
Pertanto, se
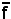 (P) = (x' + ix'', y' + iy''),
(P) = (x' + ix'', y' + iy''),
deve accadere che
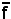 (
(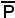 ) = (x' - ix'', y' - iy''),
) = (x' - ix'', y' - iy''),
quindi
P =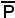
 P reale.
P reale.
Le coppie di numeri associati ad un punto si chiamano coordinate del punto, se
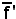

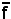

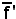 (P) = (x, y)
(P) = (x, y) C2.
C2.
Quindi, si dice che (x, y) è la coppia delle coordinate del punto P nel sistema coordinato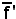 .
.
Il primo termine della coppia si chiama ascissa, il secondo ordinata.
A tal punto, s'introduce la nozione di retta, tale che la sua traccia sia una retta del piano π.
Si ricorda che, fissando su π un riferimento, l'insieme dei punti, retta, è rappresentato da un'equazione di primo grado, con la condizione che i punti appartengano alla retta se le coordinate dei punti sono soluzioni dell'equazione.
Si dice pertanto che un sottoinsieme r del piano è
una retta se e solo se esistono tre numeri, a, b, c, complessi con la
condizione che la coppia (a, b) sia diversa dalla coppia (0, 0), tali
che per ogni punto appartenente alla retta r,
è
una retta se e solo se esistono tre numeri, a, b, c, complessi con la
condizione che la coppia (a, b) sia diversa dalla coppia (0, 0), tali
che per ogni punto appartenente alla retta r, 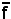 (P)
sia soluzione dell'equazione ax + by + c = 0, inoltre per ogni coppia
(x, y) di numeri complessi, soluzioni dell'equazione ax + by + c = 0, deve risultare:
(P)
sia soluzione dell'equazione ax + by + c = 0, inoltre per ogni coppia
(x, y) di numeri complessi, soluzioni dell'equazione ax + by + c = 0, deve risultare:
f-1(x, y) r,
r,
cioè
r
 retta
retta 
 a, b, c
a, b, c C, (a, b) ≠ (0, 0)
C, (a, b) ≠ (0, 0) 
 P
P r,
r, 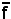 (P) soluzione dell'equazione
(P) soluzione dell'equazione
ax + by + c = 0
 (x, y)
(x, y) C2 soluzione dell'equazione ax + by + c = 0 : f-1(x, y)
C2 soluzione dell'equazione ax + by + c = 0 : f-1(x, y) r.
r.
Considerata una retta, rappresentata nel sistema coordinato f da un'equazione del tipo ax + by + c = 0, si ha che tutti i punti della retta nel piano π hanno coordinate reali, soluzioni dell'equazione e viceversa.
Se si considera cioè l'equazione nel campo complesso, le soluzioni reali sono anche soluzioni nel campo complesso, inoltre ci sono anche soluzioni complesse che rappresentano gli elementi appartenenti al piano π'.
Tale equazione rappresenta una retta e l'intersezione della retta con π dà una delle solite rette considerate nella geometria elementare.
Si possono verificare i seguenti casi.
1)-Nell'estensione complessa del piano, una retta si dice reale se la sua equazione nel sistema coordinato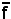 soddisfa la seguente condizione: esiste un numero ρ diverso da zero, tale che ρa, ρb, ρc, siano elementi dei numeri reali, cioè
soddisfa la seguente condizione: esiste un numero ρ diverso da zero, tale che ρa, ρb, ρc, siano elementi dei numeri reali, cioè
r reale di equazione ax + by + c = 0
 ρ ≠ 0
ρ ≠ 0  ρa, ρb, ρc
ρa, ρb, ρc R.
R.
2)-Nell'estensione complessa del piano, una retta si dice complessa e non reale se la sua equazione nel sistema coordinato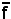 soddisfa la seguente condizione: non esiste un numero ρ diverso da zero, tale che ρa, ρb, ρc, non siano elementi dei numeri reali, cioè
soddisfa la seguente condizione: non esiste un numero ρ diverso da zero, tale che ρa, ρb, ρc, non siano elementi dei numeri reali, cioè
r complessa e non reale di equazione ax + by + c = 0
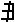 ρ ≠ 0
ρ ≠ 0  ρa, ρb, ρc
ρa, ρb, ρc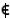 R.
R.
Se a, b, c sono complessi, possono essere anche reali.
Partendo da un'equazione a coefficienti reali, moltiplicando per i si ottiene una retta non reale.
Proprietà relative alle rette reali
In tal caso, i coefficienti dell'equazione si devono sempre considerare reali.
Si suppone che l'equazione della retta reale sia la seguente:
(α + iα')x + (β + iβ')y + (γ + iγ') = 0.
Si dimostra ora che la retta è reale, per tale motivo la matrice formata dalle righe α, β, γ ed α', β', γ' ha rango 1, cioè:
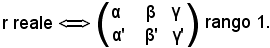
Aggiungendo alla seconda riga la terza:
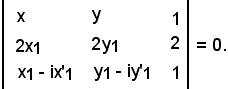
Siccome gli elementi della seconda riga sono proporzionali ad x1 ed a y1 secondo il numero 2:
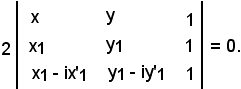
Sottraendo alla terza riga la seconda:
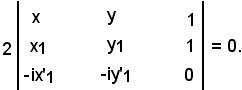
Siccome gli elementi della terza riga sono proporzionali ad x1 ed a y1 secondo -i:
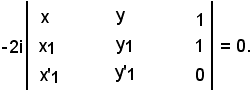
Dividendo per -2i:
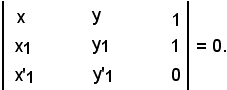
Siccome tale equazione ha coefficienti reali, la retta è reale.
3)-Considerati una retta reale r ed un punto complesso P appartenente ad essa, anche il complesso e coniugato di P appartiene ad r, cioè:
r reale, P r
r 
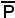 complesso e coniugato di P
complesso e coniugato di P 
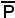
 r.
r.
Dimostrazione 3).
Si supponga che il punto P abbia le seguenti coordinate
P(x1 + ix'1, y1 + iy'1),
e che r abbia equazione
ax + by + c = 0,
a R, b
R, b R, c
R, c R, (a, b) ≠ (0, 0).
R, (a, b) ≠ (0, 0).
Si osserva ora che
P r
r  a(x1 + ix'1) + b(y1 + iy'1) + c = 0.
a(x1 + ix'1) + b(y1 + iy'1) + c = 0.
Siccome a, b, c sono reali prefissati, affinchè il numero complesso sia uguale a zero, è necessario che sia
ax1 + by1 + c = 0, i(ax'1 + by'1) = 0 (ax1 + by1 + c) - i(ax'1 + by'1) = 0
(ax1 + by1 + c) - i(ax'1 + by'1) = 0 
 a(x1 - ix'1) + b(y1 - iy'1) + c = 0
a(x1 - ix'1) + b(y1 - iy'1) + c = 0 
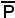 (x1 - ix'1, y1 - iy'1)
(x1 - ix'1, y1 - iy'1) r,
r,
come volevasi dimostrare.
4)-Considerata una retta r di equazione
(α + iα')x + (β + iβ')y + (γ + iγ') = 0,
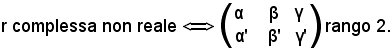
Dimostrazione 4).
Si osserva prima che se in una retta complessa non reale esiste qualche punto reale, esso è unico, quindi

Si considerano ora l'equazione suddetta della retta r ed il punto P(x1, y1), con x1 R, y1
R, y1 R, da ciò consegue che
R, da ciò consegue che
(α + iα')x1 + (β + iβ')y1 + (γ + iγ') = 0,
con
α, β, γ, α', β', γ' R
R  αx1 + βy1 + γ = 0, α'x1 + β'y1 + γ' = 0
αx1 + βy1 + γ = 0, α'x1 + β'y1 + γ' = 0  (x1, y1) soluzione del sistema
(x1, y1) soluzione del sistema 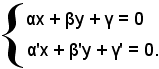
Siccome il sistema ammette una soluzione, la matrice dei coefficienti delle incognite ha rango 2, pertanto deve risultare
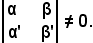
Analogamente, si dimostra l'implicazione inversa.
Per quanto ora visto, la seguente equivalenza ha anche il suo significato logico:
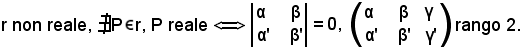
Nozione di parallelismo sull'estensione di un piano complesso
Si dice che due rette sono parallele se coincidono oppure non hanno alcun punto in comune.
Il parallelismo fra rette gode delle stesse proprietà già viste anche nell'estensione della retta nel piano complesso:
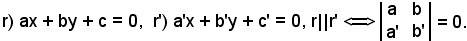
Per tale relazione, valgono gli stessi ragionamenti già fatti.
Si trova ora la condizione necessaria e sufficiente affinchè una retta complessa sia parallela ad una retta reale; si dimostra che
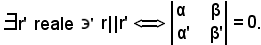
Se la retta è già reale, fra le sue equazioni ne esiste una in cui α, β, α' e β' siano uguali a zero.
A tal punto, si osserva che
 r' reale r') ax + by + c = 0, a
r' reale r') ax + by + c = 0, a R, b
R, b R, c
R, c R, r||r',
R, r||r',  ρ≠0, a = ρ(α + iα'), b = ρ(β + iβ')
ρ≠0, a = ρ(α + iα'), b = ρ(β + iβ') 

 ρ = ρ' + iρ''
ρ = ρ' + iρ''  (ρ', ρ'') ≠ (0, 0), (ρ' + iρ'')(α + iα'), (ρ' + iρ'')(β + iβ')
(ρ', ρ'') ≠ (0, 0), (ρ' + iρ'')(α + iα'), (ρ' + iρ'')(β + iβ') 

 ρ'
ρ' R,
R,  ρ''
ρ'' R
R  (ρ', ρ'') ≠ (0, 0), ρ'α' + ρ''α = 0, ρ'β' + ρ''β = 0
(ρ', ρ'') ≠ (0, 0), ρ'α' + ρ''α = 0, ρ'β' + ρ''β = 0 
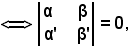
come volevasi dimostrare.
Si può quindi dire che:
una retta complessa non reale o ha un solo punto reale oppure ha una direzione reale.
Rette complesse e coniugate
Sia assegnata una retta
r) (α + iα')x + (β + iβ')y + (γ + iγ') = 0,
si dice che
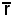 è complessa e coniugata di r
è complessa e coniugata di r  (α + iα')x + (β + iβ')y + (γ + iγ') = 0
(α + iα')x + (β + iβ')y + (γ + iγ') = 0
Si deduce subito che una retta è uguale alla sua complessa e coniugata se e solo se r è reale:
r =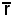
 r è reale.
r è reale.
Caso di rette complesse e coniugate distinte
Si dimostra che: se due rette complesse e coniugate distinte non sono parallele, cioè sono incidenti, il punto di incidenza è reale.
E' bene aggiungere anche che se due rette complesse e coniugate sono parallele, la loro direzione è reale.
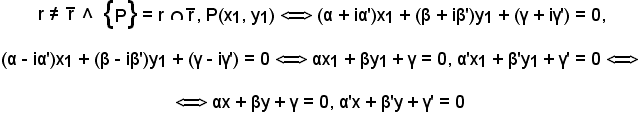
ha (x1, y1) come soluzione.
Tale soluzione è reale, quindi il punto di incidenza è reale, pertanto
P = f-1(x1, y1) reale,
come volevasi dimostrare.
Si dimostra ora che se le rette complesse e coniugate sono parallele, la direzione è reale.
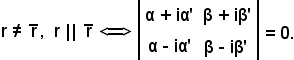
Aggiungendo la seconda riga alla prima, si ha:
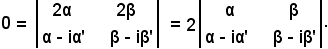
Sottraendo alla seconda riga la prima, si ha:
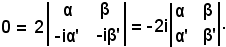
Siccome -2i non è nullo, necessariamente dev'essere
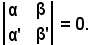
Questa è la condizione affinchè esista una retta reale parallela alla retta r, ma poichè r è parallela ad , r ed
, r ed  hanno una direzione reale.
hanno una direzione reale.
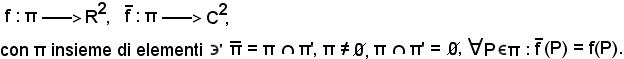
Si considera ora l'insieme (
essendo
Si chiama estensione complessa di π la coppia formata da da
(
Gli elementi di quest'estensione complessa si chiamano punti complessi, mentre (
Si osserva ora che:
P reale
Dunque, se P è reale, la coppia associata è sempre reale.
Siccome
Definizione - Si dice che due punti P e
((
sono coppie di numeri complessi e coniugati.
Pertanto, se
deve accadere che
quindi
P =
Le coppie di numeri associati ad un punto si chiamano coordinate del punto, se
Quindi, si dice che (x, y) è la coppia delle coordinate del punto P nel sistema coordinato
Il primo termine della coppia si chiama ascissa, il secondo ordinata.
A tal punto, s'introduce la nozione di retta, tale che la sua traccia sia una retta del piano π.
Si ricorda che, fissando su π un riferimento, l'insieme dei punti, retta, è rappresentato da un'equazione di primo grado, con la condizione che i punti appartengano alla retta se le coordinate dei punti sono soluzioni dell'equazione.
Si dice pertanto che un sottoinsieme r del piano
f-1(x, y)
cioè
r
ax + by + c = 0
Considerata una retta, rappresentata nel sistema coordinato f da un'equazione del tipo ax + by + c = 0, si ha che tutti i punti della retta nel piano π hanno coordinate reali, soluzioni dell'equazione e viceversa.
Se si considera cioè l'equazione nel campo complesso, le soluzioni reali sono anche soluzioni nel campo complesso, inoltre ci sono anche soluzioni complesse che rappresentano gli elementi appartenenti al piano π'.
Tale equazione rappresenta una retta e l'intersezione della retta con π dà una delle solite rette considerate nella geometria elementare.
Si possono verificare i seguenti casi.
1)-Nell'estensione complessa del piano, una retta si dice reale se la sua equazione nel sistema coordinato
r reale di equazione ax + by + c = 0
2)-Nell'estensione complessa del piano, una retta si dice complessa e non reale se la sua equazione nel sistema coordinato
r complessa e non reale di equazione ax + by + c = 0
Se a, b, c sono complessi, possono essere anche reali.
Partendo da un'equazione a coefficienti reali, moltiplicando per i si ottiene una retta non reale.
Proprietà relative alle rette reali
In tal caso, i coefficienti dell'equazione si devono sempre considerare reali.
Si suppone che l'equazione della retta reale sia la seguente:
(α + iα')x + (β + iβ')y + (γ + iγ') = 0.
Si dimostra ora che la retta è reale, per tale motivo la matrice formata dalle righe α, β, γ ed α', β', γ' ha rango 1, cioè:
Dimostrazione
r reale
 ρ = ρ' + iρ'' ≠ 0, ρ' e ρ'' non entrambi nulli,
ρ = ρ' + iρ'' ≠ 0, ρ' e ρ'' non entrambi nulli,  (ρ' + iρ'')(α + iα')
(ρ' + iρ'')(α + iα') R,
R,
(ρ' + iρ'')(β + iβ') R, (ρ' + iρ'')(γ + iγ')
R, (ρ' + iρ'')(γ + iγ') R
R 
 (ρ', ρ'')
(ρ', ρ'') R, (ρ', ρ'') ≠ (0, 0)
R, (ρ', ρ'') ≠ (0, 0)  αρ'' + α'ρ' = 0,
αρ'' + α'ρ' = 0,
βρ'' + β'ρ' = 0, γρ'' + γ'ρ' = 0.
Considerata la matrice suddetta, si fissa l'attenzione sui minori del secondo ordine estratti dalla matrice, pertanto essi sono nulli, poichè dalle seguenti uguaglianze si nota la proporzionalità:
αρ'' + α'ρ' = 0, βρ'' + β'ρ' = 0,
cioè esiste una combinazione lineare delle due righe mediante ρ' e ρ'' non entrambi nulli, che è nulla, quindi il rango non può essere due, né zero, poichè i termini della matrice non sono tutti nulli, necessariamente dev'essere uguale ad uno.
Viceversa, si prendano ρ' e ρ'' reali e si consideri il numero complesso c + iρ'', siccome in tale caso valgono le stesse uguaglianze suddette, vuol dire che i tre prodotti sono reali, cioè uguali a zero. Si è trovato quindi un numero complesso che moltiplicato per α, β, γ ed α', β', γ', dà elementi reali e, per definizione di retta reale, si deve concludere che la retta è reale.
Proprietà relative alla retta complessa non reale
1)-La retta congiungente due punti distinti e reali è una retta reale, cioè
A R, B
R, B R, A ≠ B
R, A ≠ B  [A, B] = r reale.
[A, B] = r reale.
Dimostrazione 1).
Si considerino i punti A(x1, y1) e B(x2, y2) le cui coordinate siano coppie di numeri reali, il che significa che:

Si è quindi dimostrato che la retta è reale, in quanto i coefficienti dell'equazione sono i complementi algebrici degli elementi della prima riga, determinanti estratti da (*), che sono reali.2)-La retta congiungente due punti complessi e coniugati distinti è una retta reale, cioè
A complesso e coniugato di B, A ≠ B [A, B] = r reale.
[A, B] = r reale.
Dimostrazione 2).
Si supponga che A e B abbiano le seguenti coordinate:
A(x1 + ix'1, y1 + iy'1), B(x1 - ix'1, y1 - iy'1),
ed inoltre che la coppia
(x'1, y'1) ≠ (0, 0).
Scrivendo l'equazione della retta sotto forma di determinante, si ha:
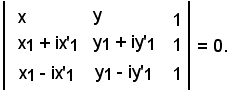
r reale
(ρ' + iρ'')(β + iβ')
βρ'' + β'ρ' = 0, γρ'' + γ'ρ' = 0.
Considerata la matrice suddetta, si fissa l'attenzione sui minori del secondo ordine estratti dalla matrice, pertanto essi sono nulli, poichè dalle seguenti uguaglianze si nota la proporzionalità:
αρ'' + α'ρ' = 0, βρ'' + β'ρ' = 0,
cioè esiste una combinazione lineare delle due righe mediante ρ' e ρ'' non entrambi nulli, che è nulla, quindi il rango non può essere due, né zero, poichè i termini della matrice non sono tutti nulli, necessariamente dev'essere uguale ad uno.
Viceversa, si prendano ρ' e ρ'' reali e si consideri il numero complesso c + iρ'', siccome in tale caso valgono le stesse uguaglianze suddette, vuol dire che i tre prodotti sono reali, cioè uguali a zero. Si è trovato quindi un numero complesso che moltiplicato per α, β, γ ed α', β', γ', dà elementi reali e, per definizione di retta reale, si deve concludere che la retta è reale.
Proprietà relative alla retta complessa non reale
1)-La retta congiungente due punti distinti e reali è una retta reale, cioè
A
Dimostrazione 1).
Si considerino i punti A(x1, y1) e B(x2, y2) le cui coordinate siano coppie di numeri reali, il che significa che:

Si è quindi dimostrato che la retta è reale, in quanto i coefficienti dell'equazione sono i complementi algebrici degli elementi della prima riga, determinanti estratti da (*), che sono reali.
A complesso e coniugato di B, A ≠ B
Dimostrazione 2).
Si supponga che A e B abbiano le seguenti coordinate:
A(x1 + ix'1, y1 + iy'1), B(x1 - ix'1, y1 - iy'1),
ed inoltre che la coppia
(x'1, y'1) ≠ (0, 0).
Scrivendo l'equazione della retta sotto forma di determinante, si ha:
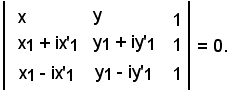
Aggiungendo alla seconda riga la terza:
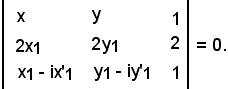
Siccome gli elementi della seconda riga sono proporzionali ad x1 ed a y1 secondo il numero 2:
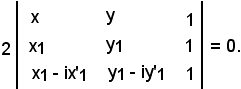
Sottraendo alla terza riga la seconda:
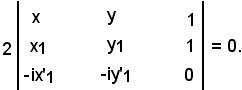
Siccome gli elementi della terza riga sono proporzionali ad x1 ed a y1 secondo -i:
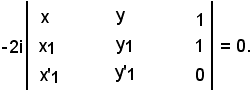
Dividendo per -2i:
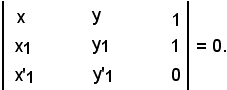
Siccome tale equazione ha coefficienti reali, la retta è reale.
3)-Considerati una retta reale r ed un punto complesso P appartenente ad essa, anche il complesso e coniugato di P appartiene ad r, cioè:
r reale, P
Dimostrazione 3).
Si supponga che il punto P abbia le seguenti coordinate
P(x1 + ix'1, y1 + iy'1),
e che r abbia equazione
ax + by + c = 0,
con
a
Si osserva ora che
P
Siccome a, b, c sono reali prefissati, affinchè il numero complesso sia uguale a zero, è necessario che sia
ax1 + by1 + c = 0, i(ax'1 + by'1) = 0
come volevasi dimostrare.
4)-Considerata una retta r di equazione
(α + iα')x + (β + iβ')y + (γ + iγ') = 0,
Dimostrazione 4).
Si osserva prima che se in una retta complessa non reale esiste qualche punto reale, esso è unico, quindi
Si considerano ora l'equazione suddetta della retta r ed il punto P(x1, y1), con x1
(α + iα')x1 + (β + iβ')y1 + (γ + iγ') = 0,
con
α, β, γ, α', β', γ'
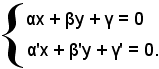
Siccome il sistema ammette una soluzione, la matrice dei coefficienti delle incognite ha rango 2, pertanto deve risultare
Analogamente, si dimostra l'implicazione inversa.
Per quanto ora visto, la seguente equivalenza ha anche il suo significato logico:
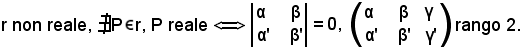
Nozione di parallelismo sull'estensione di un piano complesso
Si dice che due rette sono parallele se coincidono oppure non hanno alcun punto in comune.
Il parallelismo fra rette gode delle stesse proprietà già viste anche nell'estensione della retta nel piano complesso:
Per tale relazione, valgono gli stessi ragionamenti già fatti.
Si trova ora la condizione necessaria e sufficiente affinchè una retta complessa sia parallela ad una retta reale; si dimostra che
Se la retta è già reale, fra le sue equazioni ne esiste una in cui α, β, α' e β' siano uguali a zero.
A tal punto, si osserva che
come volevasi dimostrare.
Si può quindi dire che:
una retta complessa non reale o ha un solo punto reale oppure ha una direzione reale.
Rette complesse e coniugate
Sia assegnata una retta
r) (α + iα')x + (β + iβ')y + (γ + iγ') = 0,
si dice che
è una delle equazioni di 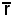 .
.
Si deduce subito che una retta è uguale alla sua complessa e coniugata se e solo se r è reale:
r =
Caso di rette complesse e coniugate distinte
Si dimostra che: se due rette complesse e coniugate distinte non sono parallele, cioè sono incidenti, il punto di incidenza è reale.
E' bene aggiungere anche che se due rette complesse e coniugate sono parallele, la loro direzione è reale.
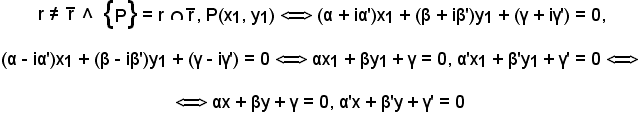
ha (x1, y1) come soluzione.
Tale soluzione è reale, quindi il punto di incidenza è reale, pertanto
P = f-1(x1, y1) reale,
come volevasi dimostrare.
Si dimostra ora che se le rette complesse e coniugate sono parallele, la direzione è reale.
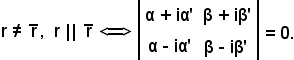
Aggiungendo la seconda riga alla prima, si ha:
Sottraendo alla seconda riga la prima, si ha:
Siccome -2i non è nullo, necessariamente dev'essere
Questa è la condizione affinchè esista una retta reale parallela alla retta r, ma poichè r è parallela ad