MATRICI ---> INDICE
Siano m ed n due interi, m ≥ 1, n ≥
1, e si considerino gli m x n numeri complessi, che possono essere
anche reali, indicati con la stessa lettera a, munita di due
indici:
ai.k,
con i = 1, 2, 3, ..., m e k = 1, 2, 3, ..., n.
Al variare di i e k si ottengono gli m x n numeri complessi, che vengono collocati in uno schema rettangolare racchiuso fra parentesi tonde:

Questo schema si chiama matrice del tipo (m, n), m x n, o anche matrice ad m righe ed n colonne.
Gli indici in basso della 1^, della 2^, dell'n-esima colonna sono 1, 2, ..., n.
Gli indici in alto della 1^, della 2^, dell'm-esima riga sono 1, 2, ..., m.
I numeri ai.k si chiamano elementi ed appartengono alla riga i-esima ed alla colonna k-esima.
Molte volte una matrice si indica con un'unica lettera A oppure con ai.k.
In particolare, se m = 1, si scrive:
a1, a2, ..., an,
tralasciando il puntino e l'indice in alto.
Se n = 1, si scrive:
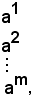
tralasciando il puntino e l'indice in basso.
Se la matrice è formata da una riga e da una colonna, si eliminano entrambi gl'indici ed i puntini.
Le matrici si indicano anche scrivendo gl'indici entrambi in alto o entrambi in basso, dove il primo indice indica la riga ed il secondo la colonna:

Criterio del confronto per matrici dello stesso tipo
Date le matrici A e B dello stesso tipo (m, n):
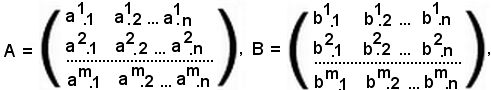
esse sono uguali se e solo se
 i = 1, 2, ..., m
i = 1, 2, ..., m 
 k = 1, 2, ..., n : ai.k = bi.k,
k = 1, 2, ..., n : ai.k = bi.k,
A = B
 i = 1, 2, ..., m
i = 1, 2, ..., m 
 k = 1, 2, ..., n : ai.k = bi.k.
k = 1, 2, ..., n : ai.k = bi.k.
In altri termini, le matrici A e B dello stesso tipo (m, n) sono uguali, se i termini che occupano lo stesso posto nelle matrici sono uguali.
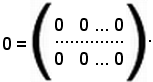
Matrice nulla
Fra le matrici del tipo m x n vi è quella nella quale tutti gli elementi sono uguali a zero; tale matrice si indica con il simbolo Om,n, cioè
Om,n matrice nulla.
matrice nulla.
Si esaminano ora alcuni argomenti necessari alla trattazione delle matrici.
Considerati n numeri, si effettua la loro somma
a1 + a2 + ... + an,
che si indica con
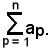
L'insieme dei valori che p assume si dice intervallo di variabilità degl'indici.
Considerati altri n numeri
b1, b2, ..., bn,
la seguente somma dei prodotti
a1b1 + a2b1 + ... + anb1
si indica con
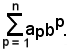
Supposto che gli n numeri b abbiano anche un indice fisso in basso:
b1.k, b2.k, ..., bn.k,
essi figurano nella colonna k-esima di una matrice.
Si considera ora la somma dei seguenti prodotti
a1b1.k + a2b2.k + ... + apbp.k,
e la si indica con
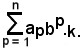
Dopo la seguente convenzione:
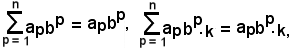
le suddette somme si possono scrivere in forme diverse esprimendo che, quando in un'espressione monomia si trovi un indice ripetuto in alto ed in basso, indice muto, di cui si conosca l'intervallo di variabilità, si somma rispetto a detto indice senza indicare il simbolo della sommatoria. Se occorre sommare rispetto a più indici ripetuti in alto ed in basso, indici muti, quando si conoscono i loro intervalli di variabilità, si usa la stessa convenzione:
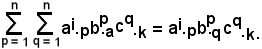
Si suppone di avere n numeri reali e si dispongono in ordine crescente:
p1, p2, ..., pn,
con
p1 < p2 < ... < pn.
Tale allineamento si dice permutazione naturale.
Ogni altro allineamento
k1, k2, ..., kn
si dice permutazione in quanto, pur essendo gli stessi numeri, cambia l'ordine di allineamento.
Se si considerano due numeri di una permutazione, ki e ki, il cui primo sia minore del secondo, si ha
i < i.
Si dice che i due numeri ki e ki formano un'inversione se e solo se risulta
ki < ki.
Se il numero delle inversioni degli elementi di una permutazione è pari, la permutazione si dice di classe pari, se è dispari, la permutazione si dice di classe dispari.
Ci si pone la seguente domanda: quante sono le possibili permutazioni distinte, se è diverso l'ordine?
Si dimostra che il numero di permutazioni di n numeri è dato dal prodotto dei primi n numeri interi naturali
n(n - 1)(n - 2)...3·2·1
e si indica con n fattoriale, cioè:
n!
Tipi di matriciSi consideri una matrice A del tipo (m, n):
-se m ≠ n, la matrice si dice rettangolare,
-se m = n, la matrice si dice quadrata; il numero n si chiama ordine della matrice quadrata e rappresenta il numero delle righe o delle colonne.
Nota bene
Non ha senso parlare di matrici rettangolari.
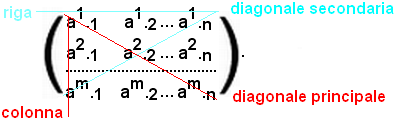
Struttura delle matriciSi consideri una matrice quadrata di ordine
n, gli elementi che hanno uguale indice in basso ed in alto si dicono
elementi della diagonale principale e si contrappongono agli elementi
della diagonale secondaria.
Determinanti delle matrici quadrate
Si considerino una matrice quadrata di ordine n ed una permutazione di n numeri:
i1, i2, ..., in;
tali permutazioni sono n!
Si indichi con i il numero delle inversioni che gli elementi della permutazione formano, si consideri il prodotto degli n fattori e si effettui la somma:
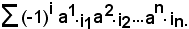
Si hanno tanti prodotti quante sono le permutazioni, la somma degli n fattoriale prodotti si chiama determinante della matrice A e si indica con
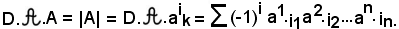
Il determinante di A è un numero, le righe e le colonne della matrice A si dicono righe e colonne del determinante di A.
Si calcola ora il determinante di una matrice A del 2° ordine:
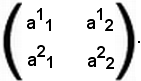
Si scrivono le permutazioni dei numeri 1 e 2:
1 e 2 non formano inversione, quindi i = 0,
2 ed 1 formano inversione, quindi i = 1.
Dunque:
|A| = (-1)0a11a22 + (-1)1a12a21 = a11a22 - a12a21.
Cioè, il determinante di una matrice quadrata del secondo ordine si ottiene effettuando la differenza dei prodotti fra gli elementi della diagonale principale e gli elementi della diagonale secondaria.
Si calcola anche il determinante di una matrice quadrata A del 3° ordine:

Si scrivono ora le permutazioni dei numeri 1, 2 e 3:
1 2 3 non formano inversioni, i = 0,
2 3 1 formano 2 inversioni, i = 2,
3 1 2 formano 2 inversioni, i = 2,
2 1 3 formano 1 inversione, i = 1,
1 3 2 formano 1 inversione, i = 1,
3 2 1 formano 3 inversioni, i = 3.
Dunque:
|A| = (-1)0a11a22a33 + (-1)2a12a23a31 + (-1)2a13a21a32 + (-1)1a12a21a33 + (-1)1a11a23a32 ++(-1)3a13a22a31 = a11a22a33 + a12a23a31+ a13a21a32 - a12a21a33 - a11a23a32 - a13a22a31.
Tale calcolo si può effettuare anche scrivendo a destra, accanto al determinante della matrice A, le prime due colonne della stessa matrice e moltiplicando opportunamente gli elementi:
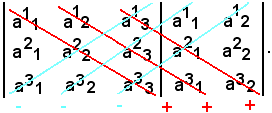
Cioè, dalle somme dei prodotti degli elementi delle diagonali rosse, si sottraggono i prodotti degli elementi delle diagonali celesti.
Si dimostra che:
-il determinante delle matrici di primo ordine è l'unico elemento della matrice A.
Infatti, si consideri la matrice
A = a11,
siccome i = 0, si ha
|A| = (-1)0a11 = a11.
Teorema 1
Si consideri la matrice
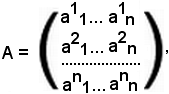
il cui determinante risulta
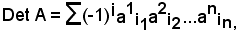
dove i rappresenta il numero delle inversioni.
Inoltre, si consideri la matrice B, ottenuta dalla matrice A moltiplicando gli elementi di una sua riga prefissata, ad esempio la prima, per uno stesso numero ρ, cioè
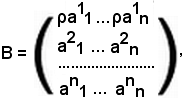
allora risulta
DetB = ρDetA.
E ciò ha senso per una matrice quadrata.
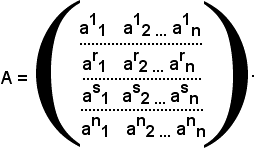
Definizione di trasposta di una matrice
Si suppone che la riga r-esima sia uguale alla riga s-esima, cioè:
ar1 = as1, ar2 = as2, ..., arn = asn,
e ciò significa che
 k = 1, ..., ark = ask.
k = 1, ..., ark = ask.
Si deve dimostrare che
DetA = 0.
Allo scopo, si consideri la matrice B ottenuta da A scambiando di posto la riga r-esima con l's-esima:
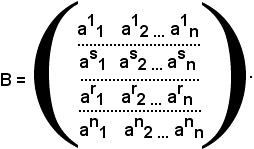
Per quanto visto in precedenza, risulta:
DetB = -DetA.
D'altronde, si sono scambiati elementi uguali e ciò non cambia nulla, pertanto
DetB = DetA,
quindi
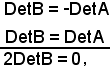
cioè
DetB = 0,
o anche
DetA = 0,
come volevasi dimostrare.
Si supponga di avere la matrice A quadrata di ordine n.
Si dice che la riga r-esima è proporzionale alla riga s-esima, se esiste ρ reale tale che
cioè
riga r-esima proporzionale alla riga s-esima
 ρ
ρ R
R 
 k = 1, ..., n : ark = ρask.
k = 1, ..., n : ark = ρask.
Si dimostra che se in una matrice vi sono due righe o due colonne proporzionali, il determinante è uguale a zero.
Si consideri la matrice
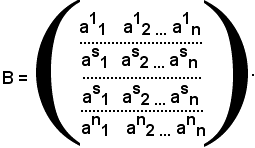
In tale matrice si è considerato
as1, as2, ..., asn
come elemento della riga r-esima, lasciando invariati gli altri.
Si osservi ora che la matrice A, ottenuta dalla matrice B moltiplicando tutti gli elementi della riga s-esima per ρ, è:
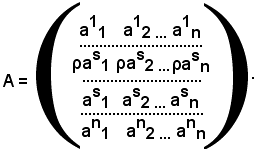
Per il teorema 1 si ha:
DetA = ρDetB,
inoltre la matrice A ha due righe uguali, pertanto
DetA = 0,
in definitiva
DetB = 0,
come volevasi dimostrare.
Si consideri la matrice
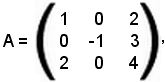
risulta
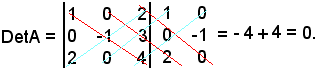
Ora, sia A una matrice qualsiasi di ordine n:
-si dice che la prima riga è combinazione lineare della seconda e della terza secondo i coefficienti λ e μ, se
 k = 1, 2, ..., n : a1k = λa2k + μa3k.
k = 1, 2, ..., n : a1k = λa2k + μa3k.

Una riga può essere combinazione lineare di più righe:
a1k = λa2k + μa3k + δa4k.
Si dimostra che:
-se in una matrice una riga è combinazione lineare di altre righe, il determinante della matrice è uguale a zero.
Esempio
Si consideri la matrice
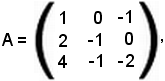
siccome la terza riga è combinazione lineare delle prime due secondo i coefficienti λ = 2 e μ = 1, si ha:
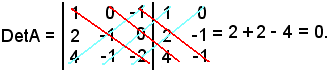
Si suppone di avere una matrice quadrata di ordine n, se agli elementi di una riga si aggiunge una combinazione lineare delle altre righe della matrice, il determinante della nuova matrice è uguale al determinante della matrice iniziale.

Cioè, si aggiunge alla terza riga una combinazione lineare della prima, della seconda e della quarta riga secondo i coefficienti λ, μ e δ:
a31 + λa11 + μa21 + δa41,
a32 + λa12 + μa22 + δa42,
a3n + λa1n + μa2n + δa4n.
Pertanto, il determinante di questa matrice è uguale al determinante della matrice inizialmente considerata.
Proprietà dei determinantiSi consideri una matrice quadrata di ordine n:

Si suppone ora che ciascun elemento di una riga sia somma di due addendi, cioè si pone
a11 = c11 + b11, a12 = c12 + b12, a1k = c1k + b1k.
A tal punto, si considerano le due matrici ottenute sostituendo gli elementi della prima riga con i primi addendi e poi con i secondi addendi, cioè:
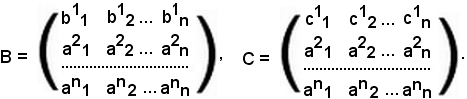
Si dimostra che:
DetA = DetB + DetC.
Esempio
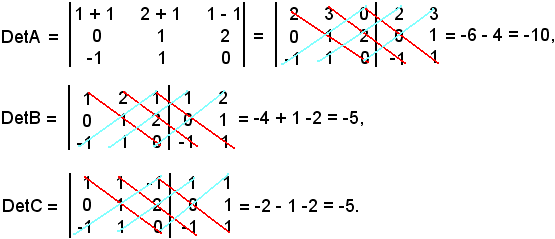
Quindi risulta
DetA = DetB + DetC = -5 - 5 = -10.
Calcolo di un determinante qualsiasi
Si consideri una matrice quadrata di ordine n:

Se si sopprimono la riga e la colonna a cui appartiene un generico elemento, ad esempio aik, i restanti elementi formano una nuova matrice quadrata di ordine n - 1:

Il determinante della matrice A' si chiama minore complementare dell'elemento aik, e si indica con
M.ki.
Si chiama complemento algebrico dell'elemento aik il minore complementare aik, preso con il proprio segno se la somma degl'indici aik è pari, mentre cambiato di segno se la somma degl'indici aik è dispari. Il complemento algebrico si indica come segue:
A.ki = (-1)i+kM.ki.
Si consideri la riga i-esima della matrice A, si dimostra che:
-la somma dei prodotti degli elementi della riga i-esima per i rispettivi complementi algebrici è uguale al determinante di A, cioè:
a|i|1A.1i + a|i|2A.2i + a|i|nA.ni = DetA,
oppure
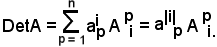
Esempio 1)
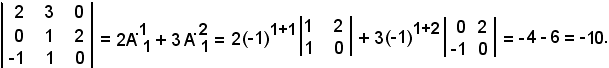
Esempio 2)
Sviluppando in base alla prima colonna

Considerando sempre lo stesso determinante, e sommando alla seconda colonna la quarta, si ha:

Si consideri una matrice

E' noto che lo sviluppo del determinante, secondo la linea i, è dato da
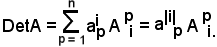
Si dimostra che la somma dei prodotti di una riga o colonna qualsiasi, per i rispettivi complementi algebrici degli elementi di un'altra riga j ≠ i, o colonna, è uguale a zero. Risulta cioè l'uguaglianza
aipApj = 0,
per j ≠ i.
In altri termini,
ai1A1j + ai2A2j + ... + ainAnj = 0.
Esempio
Si consideri la matrice
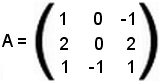
e si moltiplichi un elemento, ad esempio l'elemento 1, per il complemento algebrico del primo elemento della seconda riga:
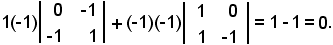
Matrice inversa
Considerata una matrice quadrata di ordine n, si dice che è non singolare se il suo determinante è diverso da zero.
Si suppone che la matrice A sia non singolare, per cui sia
DetA = Δ ≠ 0.
Un elemento qualsiasi della matrice A, ad esempio aik, si chiama elemento reciproco dell'elemento preso in considerazione. Tale elemento reciproco è uguale al complemento algebrico di aik, diviso il determinante della matrice del complemento. In altri termini:
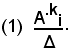
E' molto importante sapere che con i reciproci degli elementi di una matrice si può formare una nuova matrice nel seguente modo: innanzitutto si scrivono gli elementi reciproci degli elementi della prima colonna come prima riga, i reciproci degli elementi della seconda colonna come seconda riga, e così via.
La matrice così ottenuta si chiama inversa della matrice data e si indica con A-1.
Quindi l'inversa della matrice A è:
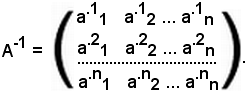
Esempio
Si consideri una matrice del terzo ordine:
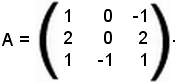
Si verifica ora se tale matrice è non singolare.
Infatti, sviluppando gli elementi della seconda colonna si ha:
Δ = -1
ed il minore complementare
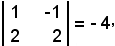
da cui
(-1)(-4) = 4.
Il primo elemento della prima riga è il reciproco di 1:
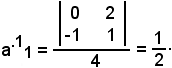
Il secondo elemento della prima riga è il reciproco di 2:
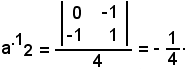
Il terzo elemento della prima riga è il reciproco di 1:
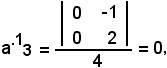
e così si procede fino ad ottenere tutti gli elementi della matrice inversa.
E' già noto che per definizione la trasposta della matrice A, indicata con A-1, è stata ottenuta scambiando nella matrice A le righe con le colonne:

Dalle nozioni di trasposta e di inversa di una data matrice si ha che, assegnata una matrice A non singolare, sia considerando prima l'inversa e poi la trasposta o viceversa, si ottiene la stessa matrice, cioè
(A-1)-1 = (A-1)-1.
Prima di dimostrare ciò, occorre prima osservare che, se si considera un elemento qualsiasi, ad esempio l'elemento aik della matrice A, esso è anche elemento della sua trasposta, inoltre il reciproco dell'elemento considerato coincide con il reciproco dello stesso elemento nella sua trasposta.
Infatti, sia data una matrice A di un certo ordine, ad esempio 3:

e si consideri la sua trasposta

Per un teorema precedente è noto che
DetA = DetA-1.
Pertanto, se si considera il reciproco di un elemento, ad esempio di a2.1 rispetto alla matrice A, si ha che a1.2 è uguale al complemento algebrico di a2.1 diviso il determinante di A, cioè
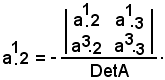
Ora, considerando il reciproco dello stesso elemento a2.1 rispetto alla trasposta della matrice A, si ha che a1.2 è uguale al complemento algebrico di a2.1 diviso il determinante di A-1, cioè
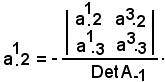
Dunque:
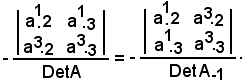
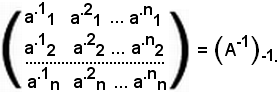
Osservato ciò, di conseguenza si dimostra che:
(A-1)-1 = (A-1)-1.
Infatti, effettuando la trasposta dell'inversa, si ha:
Inoltre, effettuando l'inversa della trasposta, si ha:
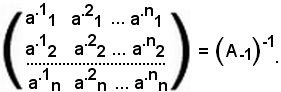
In precedenza si è visto che, considerata una matrice non singolare, risulta
a) DetA = a|i|.pA.pi,
inoltre è stato dimostrato che
ai.pA.pj = 0,
con i ≠ j.
Dividendo ambo i membri dell'uguaglianza a) per DetA, si ha:
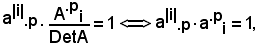
essendo
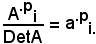
Di conseguenza, nell'uguaglianza b) si ha:
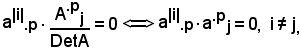
essendo
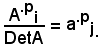
Le uguaglianze
a|i|.p·a.pi = 1, a|i|.p·a.pj = 0
si possono conglobare in un'unica uguaglianza, introducendo il simbolo di Kronecher:
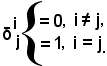
Usando tale simbolo, le due uguaglianze si possono anche scrivere:
ai.p·a.pj = δij.
Un'uguaglianza analoga si ottiene scambiando le righe con le colonne:
a.ip·ap.j = δij.
Prodotto di determinanti
Si considerino le matrici A e B dello stesso ordine:
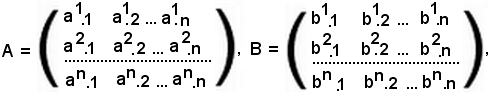
e si supponga che la matrice C sia il prodotto della matrice A per la matrice B

Quindi si ha:
A = ai.k, B = bi.k,
e sia
C = A·B.
Si ricordi inoltre che
 i = 1, ..., n,
i = 1, ..., n,  k = 1, ..., n : ci.k = ai.pbp.k
k = 1, ..., n : ci.k = ai.pbp.k
con
p = 1, ..., n.
In particolare si consideri il prodotto della matrice A per l'inversa A-1:
A·A-1 = C.
Di conseguenza, l'elemento ci.k della matrice C risulta
ci.k = ai.pap.j.
Ma
ai.pap.j = δij,
quindi
ci.j = ai.pap.j = δij.0.
Scrivendo per esteso, si ha:
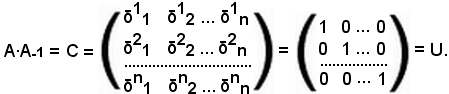
Tutti gli elementi che hanno indici distinti sono uguali a zero, mentre quelli che hanno indici uguali sono uguali ad 1.
Questa matrice si chiama matrice unità.
Ovviamente, la matrice unità è uguale alla matrice A per la sua inversa.
Essendo
DetC = DetA·DetB,
applicando tale proprietà, si ha:
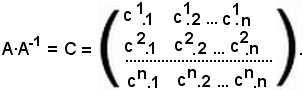
DetU = DetA·DetA-1.
Pertanto

Si è quindi ottenuto
DetA·DetA-1 = 1,
da cui
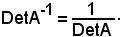
Di conseguenza, essendo A non singolare, risulta
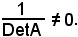
Si è quindi stabilito che l'inversa della matrice A è diversa da zero, cioè
A-1 ≠ 0,
e quindi è anch'essa non singolare; inoltre, il determinante dell'inversa di una matrice è uguale all'inverso del determinante della matrice assegnata.
Teorema 3
Si consideri la matrice

si supponga inoltre che il determinante della matrice A sia uguale a zero.
Si dimostra che esiste una sola riga, o colonna, della matrice A che è combinazione lineare di altre righe, o colonne, della stessa matrice.
Infatti, se il determinante della matrice A è uguale a zero, vuol dire che esiste una combinazione lineare nulla delle righe della matrice a coefficienti non tutti nulli, cioè che esiste una riga, ad esempio la prima, che sia combinazione lineare delle altre due.
Quindi, esistono n coefficienti tali che:
λ1a11 + λ2a21 + ... + λnan1 = 0,
λ1a12 + λ2a22 + ... + λnan2 = 0,
λ1a1n + λ2a2n + ... + λnann = 0.
Rango di una matrice
Si consideri inoltre un numero intero positivo p tale che
1 ≤ p ≤ m, 1 ≤ p ≤ n.
A tal punto, si fissano arbitrariamente p righe e p colonne; gli elementi comuni a queste p righe e p colonne formano una matrice quadrata che si chiama matrice estratta dalla matrice A.
Si suppone ora p = 2 e si scelgono, ad esempio, come righe la prima e la terza, e come colonne la seconda e l'ultima. Gli elementi comuni, come è indicato in 1), formano la seguente matrice:
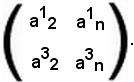
Di queste matrici ve ne sono molte, inoltre i determinanti estratti si chiamano determinanti estratti dalla matrice A.
Si dice che il numero ρ ≥ 1 è il rango o la caratteristica della matrice A se e solo se tra i determinanti estratti di ordine ρ ne esiste uno diverso da zero, e tutti i determinanti di ordine maggiore di ρ, se esistono, sono uguali a zero.
Nota bene
1)-ρ è il massimo intero positivo per cui esiste qualche determinante;
2)-se A = Om,n, per convenzione si dice che il rango della matrice A è uguale a zero, cioè per convenzione si assume rango zero per una matrice avente elementi nulli;
3)-se una matrice non è nulla, il suo rango è diverso da zero.
Si dimostra che:
-il rango di una matrice è uguale al rango della sua trasposta.
Infatti, la trasposta della matrice A è la matrice A-1, ottenuta scambiando le righe con le colonne. Allora le matrici estratte dalla trasposta di A saranno le trasposte delle matrici estratte da A. Si suppone, infatti, di fissare p righe e p colonne in A; si osserva che nella trasposta di A le righe diventano colonne. Dunque, gli elementi che appartengono alle colonne di A appartengono alle righe di A-1, e viceversa:
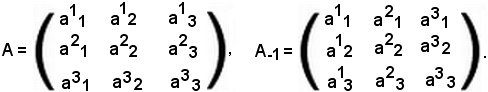
Si indichino ora con B e B-1 le matrici estratte rispettivamente da A ed A-1:
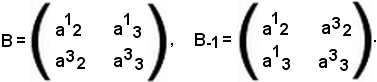
E' noto che i determinanti di due matrici quadrate, l'una trasposta dell'altra, sono uguali, allora i determinanti estratti dalla matrice A sono uguali a quelli estratti dalla trasposta di A, cioè:
DetB = DetB-1.
Se i determinanti sono gli stessi, anche il rango è lo stesso, esempio:

La terza riga è combinazione lineare delle prime due.
Si consideri un qualsiasi determinante del terzo ordine estratto dalla matrice A, anche in tal caso la terza riga è combinazione lineare delle prime due, dunque il determinante del terzo ordine è uguale a zero, e ciò accade sempre, per cui il rango non può essere uguale a tre:

C'è però almeno un determinante del secondo ordine estratto dalla matrice A, diverso da zero, per cui il rango è uguale a due:
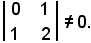
Considerata la matrice

il rango di una matrice non singolare di ordine n è uguale ad n.
Sistemi
Si consideri un sistema del tipo seguente:
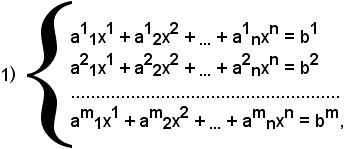
dove x1, x2, x3, ..., xn sono incognite,
a1pxp = b1 si somma per p = 1, 2, ..., n,
a11, a12, a13, ..., a1n sono reali o complessi.
Un sistema di questo tipo si chiama sistema lineare, di primo grado, di m equazioni in n incognite. Gli aik si chiamano coefficienti del sistema. I termini b1, b2, ..., bm si chiamano termini noti.
Per soluzione del sistema s'intende un'enupla di numeri
x10, x20, ..., xn0
che, sostituiti alle variabili, soddisfano il sistema.
Se il sistema ammette una soluzione si dice compatibile, se non ammette una soluzione si dice incompatibile.
Se tutti i termini noti sono uguali a zero, il sistema si dice omogeneo.
Si dimostra che tutti i sistemi omogenei sono compatibili.
Infatti, supponendo che l'enupla di numeri
x10, x20, ..., xn0
sia uguale a zero, cioè tale che
x1 = 0, x2 = 0, ..., xn = 0,
si ha una soluzione nulla o banale.
Il numero delle equazioni è uguale al numero delle incognite.
Nel caso in cui m = n si ottiene un sistema lineare omogeneo di n equazioni in n incognite. Con i coefficienti di questo sistema, si può formare una matrice quadrata di ordine n data da

Tale matrice si chiama matrice dei coefficienti del sistema.
Si dimostra che:
A non singolare il sistema ammette solo la soluzione nulla.
il sistema ammette solo la soluzione nulla.
Si consideri un sistema lineare di n equazioni in n incognite non omogeneo, e sia A la matrice dei coefficienti. Se la matrice è non singolare, il sistema ammette una ed una sola soluzione, e questa si calcola, ad esempio, con la regola di Cramer.
Si procede come segue:
si considera la prima incognita uguale ad una frazione avente per numeratore il determinante della matrice ottenuta da A, sostituendo alla prima colonna quella dei termini noti.

Esempio
Si consideri il seguente sistema non omogeneo
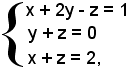
e sia A la matrice dei coefficienti:
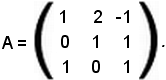
Si calcola ora il determinante di tale matrice:

Quindi:
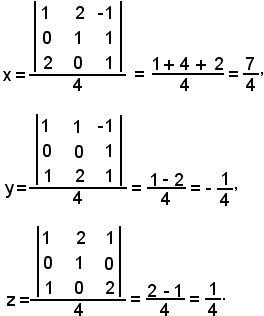
Teorema di Rouché Capelli
Tale teorema permette di stabilire se un qualsiasi sistema lineare è compatibile.
Si consideri un sistema lineare di m equazioni in n incognite:
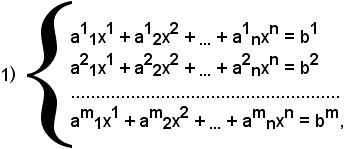
e si costruisca la matrice A dei coefficienti delle equazioni e la matrice B dei coefficienti e dei termini noti.
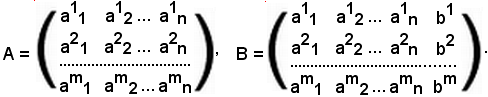
Condizione necessaria e sufficiente affinchè il sistema sia compatibile, è che le matrici A e B abbiano lo stesso rango.
Tale teorema vale anche quando il sistema è omogeneo.
Infatti, se i termini noti sono tutti nulli, allora le matrici estratte da A sono anche estratte da B, ma alcune matrici estratte da B, quelle contenenti la colonna nulla, non sono estratte da A, e ciò è interessante perchè il determinante di tali matrici è uguale a zero.
Dunque, anche in tal caso A e B hanno lo stesso rango.
Il teorema ora visto assicura l'esistenza delle soluzioni, però per trovarle si adotta il metodo seguente.
Si supponga che A e B abbiano lo stesso rango, che è detto rango del sistema. Si consideri inoltre il determinante di ordine ρ, estratto da A e diverso da zero, che si suppone essere formato dalle prime ρ righe e ρ colonne della matrice A, cioè:

Si consideri ora il sistema formato dalle ρ equazioni, i cui coefficienti figurano nel determinante suddetto:
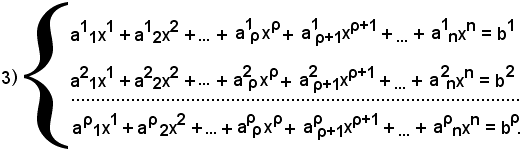
Si dimostra che il sistema 1) di m equazioni è equivalente al sistema 3) di ρ equazioni, in tal modo sono state scartate m - ρ equazioni e nel determinante 2) si avranno i coefficienti di ρ incognite.
Si considerano ora le m - ρ incognite (cioè xρ+1, xρ+2, xn), i cui coefficienti non figurano in tale determinante, e si considerano le seguenti posizioni:
xρ+1 = kρ+1, xρ+2 = kρ+2, xn = kn,
con kρ+1, kρ+2, kn numeri arbitrari.
Tali numeri si sostituiscono nel sistema 3) e si ottiene il seguente sistema 4):
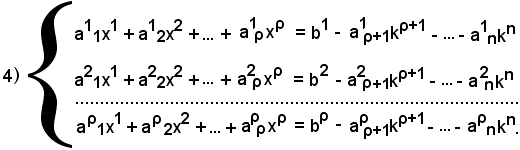
Si è così ottenuto un sistema di ρ equazioni in ρ incognite, la cui matrice dei coefficienti è nota, ed il cui determinante è il 2), ed è diverso da zero. Il sistema 4), essendo di ρ equazioni in ρ incognite, ammette una ed una sola soluzione e si risolve con la regola di Cramer.
Evidentemente, la soluzione dipende dal valore arbitrario di k, ad ogni modo comunque si fissa k si ha un'unica soluzione:
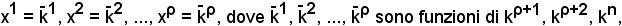
ed al loro variare, si hanno varie soluzioni del sistema.
Si può quindi asserire che
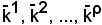
sono le generiche soluzioni del sistema 1).
Si osserva che

Si fissano dunque m - ρ in infiniti modi; si dice che il sistema ammette infinito m - ρ soluzioni.
Esempio 1): sistema di quattro equazioni in due incognite.
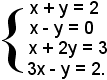
Per vedere se tale sistema è compatibile, si considera la matrice A dei coefficienti, che è del tipo (4, 2), e la matrice B, che è del tipo (4, 3), dei coefficienti delle incognite e dei termini noti:
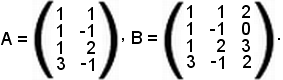
Il rango della matrice A è uguale a due, poichè esiste un estratto del secondo ordine il cui determinante è diverso da zero. Il rango della matrice B è uguale a due e non a tre, poichè i determinanti degli estratti del terzo ordine sono tutti uguali a zero, essendo la terza colonna combinazione lineare delle altre due; il rango non può essere minore di due, poichè gli estratti da A sono uguali a quelli di B e dunque, essendo due il rango di A, tale è quello di B. Si considera ora il seguente determinante del secondo ordine estratto da A
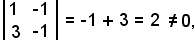
e si considerano le equazioni, i cui coefficienti figurano nel determinante ora scelto:
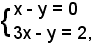
tale sistema equivale a quello iniziale e quest'ultimo si risolve con la regola di Cramer.
Esempio 2): sistema di tre equazioni in tre incognite.
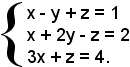
Si considera prima la matrice A dei coefficienti e poi la matrice B dei coefficienti delle incognite e dei termini noti:
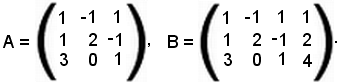
Il determinante della matrice A è uguale a zero, poichè la terza riga è combinazione lineare delle altre due, dunque il rango non è tre ma due, poichè esiste qualche determinante del secondo ordine estratto da A che è diverso da zero. Anche il rango della matrice B non è uguale a tre, poichè la terza riga è combinazione lineare delle altre due, dunque il rango è due.
Il sistema dato è quindi compatibile, ed ammette infinito ad uno soluzioni.
Si fissa ad arbitrio il valore di un'incognita e si considera un determinante di ordine due diverso da zero, estratto dalla matrice A:
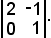
Dunque, si scrivono le ultime due equazioni:
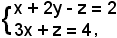
il cui sistema è equivalente a quello iniziale.
Ponendo
x = k,
si ha:
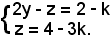
Sommando membro a membro, risulta:
2y - z + z = 2 - k + 4 - 3k,
o anche
2y = 6 - 4k,
da cui
y = 3 - 2k.
Quindi la soluzione del sistema è
x = k, y = 3 - 2k, z = 4 - 3k.
Si vuol vedere ora se un sistema omogeneo ammette soluzione diversa da quella banale; a tal fine sussiste il seguente teorema.
Teorema
Condizione necessaria e sufficiente affinchè un sistema lineare omogeneo di m equazioni in n incognite ammetta soluzioni diverse da quella banale, è che la matrice dei coefficienti abbia rango minore del numero delle incognite.
Le radici si trovano allo stesso modo dei sistemi lineari non omogenei.
Esempio: si consideri il seguente sistema lineare omogeneo di tre equazioni in tre incognite.
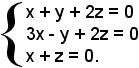
Per trovare le soluzioni si considera la matrice dei coefficienti dell'equazione:
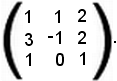
Essendo il determinante di tale matrice uguale a zero, il rango della matrice dei coefficienti non può essere tre ma è due, perchè il determinante estratto è diverso da zero, cioè:
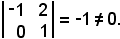
Dunque, il sistema ammette una soluzione diversa da quella banale perchè il rango è minore del numero delle incognite.
Si considerano ora le equazioni i cui coefficienti figurano nel minore estratto della matrice dei coefficienti:
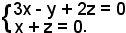
Ponendo
x = k,
si ha:
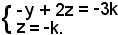
Il sistema ha dunque la soluzione generale
x = k, y = k, z = -k.
Se si dà a k il valore zero, si ha la soluzione banale; se si dà a k un valore diverso da zero, si ha la soluzione non banale.
Per risolvere un sistema omogeneo si usa un altro metodo, però prima si osserva quanto segue.
Si suppone che
x10 x20 ... xn0
sia una soluzione di un sistema omogeneo, λ un numero complesso ed inoltre si consideri la seguente enupla
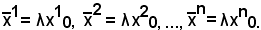
Si dimostra che anche l'enupla
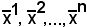
è una soluzione del sistema.
Allo scopo, è sufficiente dimostrare che
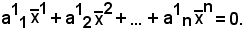
Infatti:
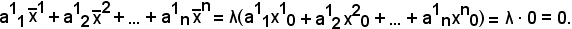
Si vede ora un altro metodo per risolvere particolari sistemi omogenei.
Si considera un sistema omogeneo di n-1 equazioni in n incognite:
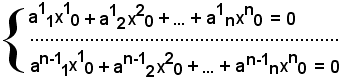
e si suppone che il rango della matrice dei coefficienti sia n-1. Per tale motivo, il sistema ammette soluzioni non banali, inoltre per trovare le soluzioni del sistema si procede come segue.
Allo scopo, si considera la matrice dei coefficienti del sistema:

Si assume per x1 il determinante estratto dalla matrice dei coefficienti, sopprimendo la prima colonna; per x2 il determinante estratto dalla matrice data, sopprimendo la seconda colonna; e così via:
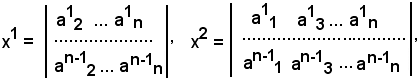
e per un generico p
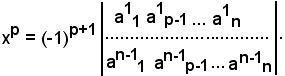
In tal modo, il sistema ammette una sola soluzione, per ottenerle tutte basta moltiplicare i determinanti estratti per un parametro k.
Esempio: si consideri il seguente sistema lineare omogeneo di tre equazioni in tre incognite.
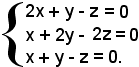
Il determinante dei coefficienti dell'equazione è uguale a zero, cioè:
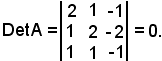
Infatti, moltiplicando la terza riga per 3, si ha:
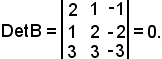
Siccome
DetB = 3DetA,
si ha
3DetA = 0,
cioè
DetA = 0.
Dunque, il rango di A non è 3 ma 2, in quanto esiste il determinante
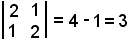
estratto da A, che è diverso da zero.
Il sistema iniziale è dunque equivalente al seguente:
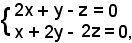
che è a due equazioni e tre incognite.
Tale sistema si risolve con il metodo espresso in precedenza e si ha:
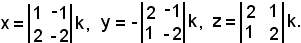
In definitiva, le soluzioni sono date da:
x = 0, y = 3k, z = 3k.
Si suppone ora di avere un sistema lineare omogeneo di m equazioni in n incognite e sia m < n. Ci si chiede se tale sistema ammette soluzioni diverse da quella banale.
Infatti, affinchè ammetta soluzioni diverse da quella banale, occorre che il rango della matrice dei coefficienti sia minore del numero delle incognite.
In tal caso il rango ρ non si conosce, ma è noto che ρ ≤ m, e poichè m < n , si ha ρ ≤ n.
Se ρ ≤ n, allora il sistema ammette certamente soluzioni diverse da quella banale.
A completamento dello studio delle matrici, si richiamano concetti già visti e si forniscono ulteriori definizioni ed esempi.
Prodotto fra numeri complessi e matrici
Sia ρ un numero complesso, cioè ρ C, ed A una matrice.
C, ed A una matrice.
Per prodotto del numero complesso ρ per la matrice A s'intende la matrice ottenuta moltiplicando tutti gli elementi della matrice A per ρ; essa si indica con ρA e risulta:
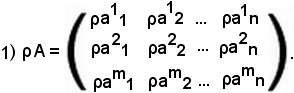
Se per caso la matrice A è quadrata di ordine n, cioè A(n, n), anche la matrice prodotto ρA è dello stesso ordine e si ha:
2) DetρA = ρnDetA.
Per stabilire tale relazione, si procede come segue. Si indica con DetρA il determinante della matrice prodotto di ρ con A, e con DetA il determinante della matrice A, pertanto risulta:
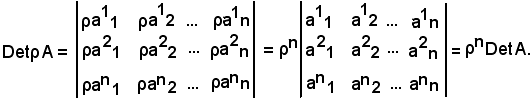
Quindi si ha:
DetρA = ρnDetA.
Esempio
Siano assegnati
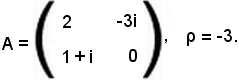
La matrice prodotto risulta
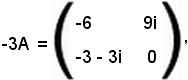
quindi,
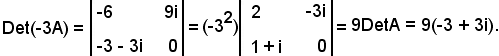
A = aik, ρA = ρaik, Aρ = aikρ,
ed essendo
ρA = Aρ,
risulta anche
ρaik = aikρ.
Matrici somma di due matrici
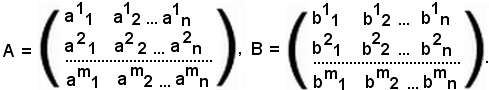
Questa matrice prende il nome di matrice somma ed è dello stesso ordine delle matrici A e B.
Se
A = aik, B = bik,
con
i = 1, 2, ..., m e k = 1, 2, ..., n,
la matrice somma è espressa da
A + B = aik + bik.
Se si considera la matrice B + A, si ha:
B + A = bik + aik.
Le matrici A + B e B + A hanno gli elementi comuni uguali e pertanto, essendo
aik + bik = bik + aik,
risulta
A + B = B + A.
Ciò conferma che anche le matrici godono della proprietà commutativa.
Si consideri ora un'ulteriore matrice
C = cik,
si asserisce che le matrici godono della proprietà associativa:
(A + B) + C = A + (B + C).
Essendo
(A + B) + C = (aik + bik) + cik,
A + (B + C) = aik + (bik + cik),
risulta
(aik + bik) + cik = aik + (bik + cik),
quindi le nuove matrici sono:
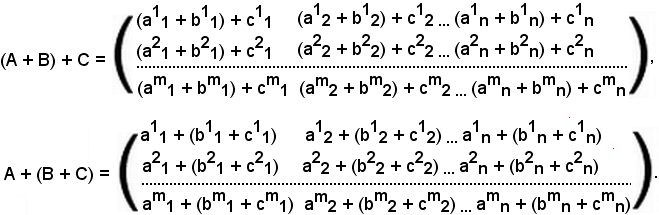
Si considerino tre matrici del tipo (m, n):
A = aik, B = bik, C = cik,
e siano inoltre λ, μ, δ tre numeri complessi.
Si possono ora considerare le matrici e le combinazioni lineari di A, B, C secondo λ, μ e δ:
λA = λaik, μB = μbik, δC = δcik,
cioè
λA + μB + δC = λaik + μbik + δcik.
Esempio
Si considerano due matrici del tipo (2, 3)
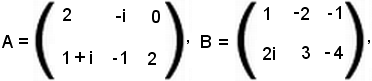
si ha:
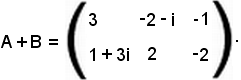
Fra le matrici del tipo (m, n), si considerino tutte quelle che hanno i = 0; indicando tale matrice con zero, si ha:
Se a tale matrice si somma una matrice A del tipo (m, n), si ha:
A + 0 = A = 0 + A.
Se si ha una matrice A, si può determinare una matrice X dello stesso tipo, tale che:
A + X = 0, X = -A,
quindi risulta anche
aik + xik = 0, xik = -aik,
essendo
A = aik, X = xik.
In tal caso, gli elementi della matrice X sono opposti a quelli della matrice A.
Siano A una matrice del tipo (m, n), α e β due numeri complessi. Siccome α·β è un numero complesso, si può sempre considerare la matrice A per α·β, cioè:
1) (α·β)A = α(βA) = β(αA) = αβA.
Se A ha aik elementi, il generico elemento della matrice (α·β)A è (αβ)aik per ogni i = 1, 2, ..., m e k = 1, 2, ..., n, pertanto si ha:
2) (αβ)aik = α(βaik) = β(αaik).
Nelle uguaglianze 1) e 2), come si può notare, valgono sempre le proprietà commutativa ed associativa.
Inoltre, si può parlare della proprietà distributiva della somma rispetto al prodotto.
Siano A e B due matrici del tipo (m, n),
A = aik, B = bik,
con i = 1, 2, ..., m e k = 1, 2, ..., n, ed α un numero complesso.
Si considerino ora la matrice somma A + B e la matrice prodotto α(A + B).
Si dimostra che
3) α(A + B) = αA + αB = Aα + Bα = (A + B)α,
e che quindi la proprietà distributiva vale sia a destra che a sinistra.
Rispetto alla i-esima riga ed alla k-esima colonna, la matrice α(A + B) ha rispettivamente i seguenti elementi:
α(aik + bik),
mentre i corrispondenti elementi delle matrici αA ed αB sono:
αaik + αbik.
Analogamente alla 3), si ha:
α(aik + bik) = αaik + αbik = aikα + bikα = (aik + bik)α.
Se A e B sono matrici quadrate dello stesso ordine, la matrice somma A + B è sempre una matrice quadrata dello stesso ordine. In generale, risulta:
Det(A + B) ≠ DetA + DetB.
Si considerino una matrice A del tipo (h, m) ed una matrice B del tipo (m, l) e si faccia in modo che il numero delle colonne di A sia uguale al numero delle righe di B:
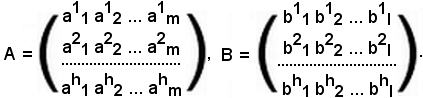
c11 = 4 - 2i - 2i - 1 = 3 - 4i, c21 = 2i + 6.
Si consideri ora il caso in cui la matrice A sia del tipo (h, m) e la matrice B del tipo (m, h) e si indichi con AB una matrice di ordine h, cioè del tipo (h, h), e con BA una matrice di ordine m, cioè del tipo (m, m), con h ≠ m; pertanto, risulta
AB ≠ BA.
Si osserva che se h = m, AB e BA sono matrici di ordine m; inoltre, risulta:
AB = apibiq,
BA = bpiaiq,
e poichè
AB = BA,
si ha:
apibiq = bpiaiq.
Quindi, in generale, si può dire che il prodotto gode della proprietà commutativa.
Esempio
Si considerino le matrici A del tipo (2, 3) e B del tipo (3, 1):
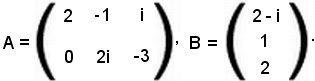
La matrice prodotto AB è del tipo (2, 1), cioè
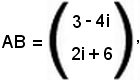
in cui
c11 = 4 - 2i - 2i - 1 = 3 - 4i, c21 = 2i + 6.
Si consideri ora il caso in cui la matrice A sia del tipo (h, m) e la matrice B del tipo (m, h), e si indichi con AB una matrice di ordine h, cioè del tipo (h, h), e con BA una matrice di ordine m, cioè del tipo (m, m), con h ≠ m; pertanto, risulta
AB ≠ BA.
Si osserva che se h = m, AB e BA sono matrici di ordine m; inoltre, risulta:
AB = apibiq,
BA = bpiaiq,
e poichè
AB = BA,
si ha:
apibiq = bpiaiq.
Quindi, in generale, si può dire che il prodotto gode della proprietà commutativa.
Esempio
Si considerino le seguenti matrici:
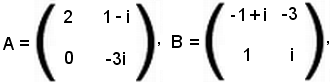
la matrice prodotto AB risulta
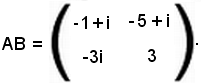
In tale matrice gli elementi della prima riga sono stati calcolati come segue:
1° elemento: 2(-1 + i) + 1 - i = -2 + 2i + 1 - i = -1 + i;
2° elemento: -6 + (1 - i) = -6 + 1 + i = -5 + i.
Gli elementi della seconda riga sono: -3i e 3.
Inoltre, la matrice prodotto BA risulta
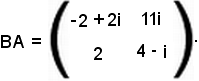
In tale matrice gli elementi della prima e della seconda riga sono stati calcolati come segue:
1° elemento della prima riga: 2(-1 + i) + 0 = -2 + 2i;
2° elemento della prima riga: 11i;
1° elemento della seconda riga: 2;
2° elemento della seconda riga: 4 - i.
Si calcolano ora i seguenti determinanti:
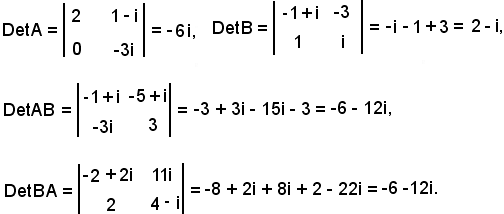
In tal modo è dimostrato che:
DetAB = DetBA.
Si considerino tre matrici A, B, C rispettivamente di termini generici aik, bik, cik e di tipo (h, m), (m, l), (l, s), cioè
A = aik, B = bik, C = cik.
Tali matrici godono delle proprietà distributiva, commutativa e associativa.
Pertanto si consideri
1) (AB)C = (apibiq)cqt,
di tipo (h, s); t si chiama indice muto.
2) A(BC) = apj(biqcqt),
di tipo (h, s); j si chiama indice muto.
Applicando la proprietà distributiva alla 2), si ha:
apj(biqcqt) = apjbiqcqt,
e quindi
(AB)C = A(BC) = ABC.
Proprietà delle matrici
Considerate due matrici
A = aik, B = bst,
rispettivamente di tipo (h, m) ed (m, l), si può definire la matrice
AB = cpq = cpqbiq,
che è di tipo (h, l).
Si considerino inoltre un numero complesso α e la matrice prodotto di α per AB; si dimostra quanto segue:
α(AB) = (αA)B = A(αB).
Basta dimostrare che gli elementi della matrice α(AB) sono uguali a quelli della matrice (αA)B che, rispetto alla p-esima ed alla q-esima colonna, hanno elementi
αcpq = α(apibiq),
dove quest'ultimi sono numeri complessi e godono della proprietà distributiva, pertanto si ha:
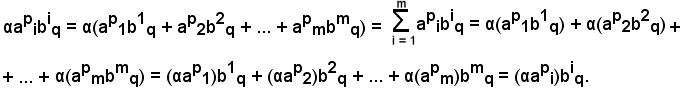
Quest'ultimo elemento è quello corrispondente della matrice (αA)B e tale uguaglianza dimostra che
α(AB) = (αA)B.
Analogamente, si dimostra che
α(AB) = A(αB).
Pertanto, per le proprietà commutativa e associativa dei numeri complessi:
α(apibiq) = api(αbip).
Si considerino tre matrici A, B, C rispettivamente di termini generici aik, bst, cst e di tipo (h, m), (m, l), (m, l), cioè
A = aik, B = bst, C = cst.
Si può parlare di matrice somma del tipo (m, l), cioè
B + C = bst + cst.
Si dimostra che
A(B + C) = AB + AC,
cioè che vale la proprietà distributiva a sinistra.
Si considerano gli elementi generici
api(biq + ciq),
che rappresentano numeri complessi, quindi fissato i si può considerare la somma dei prodotti. Applicando la proprietà distributiva, si può considerare:
api(biq + ciq) = apibiq + apiciq.
D'altronde
api(biq + ciq) = ap1(b1q + c1q) + ap2(b2q + c2q) + ... = ap1b1q + ap1c1q + ap2b2q + ap2c2q +
+ ... = ap1b1q + ap2b2q + ap1c1q + ap2c2q + ... = apibiq + apiciq.
apiciq è il termine corrispondente in AC, apibiq è il termine corrispondente in AB, quindi:
A(B + C) = AB + AC.
Analogamente, se si considerano tre matrici A, B, C rispettivamente di termini generici aik, bik, cst di tipo (h, m), (h, m), (m, l), cioè
A = aik, B = bik, C = cst,
si può parlare di matrice somma A + B del tipo (h, m) e si può considerare la proprietà distributiva a destra, cioè
(A + B)C = AC + BC.
La dimostrazione è analoga alla precedente.
Matrice unità
Si considera una matrice quadrata di ordine n, indicata con U, e si indicano con δki i suoi elementi con i, k = 1, 2, ... n. Quindi
U = δki.
ai.k,
con i = 1, 2, 3, ..., m e k = 1, 2, 3, ..., n.
Al variare di i e k si ottengono gli m x n numeri complessi, che vengono collocati in uno schema rettangolare racchiuso fra parentesi tonde:

Questo schema si chiama matrice del tipo (m, n), m x n, o anche matrice ad m righe ed n colonne.
Gli indici in basso della 1^, della 2^, dell'n-esima colonna sono 1, 2, ..., n.
Gli indici in alto della 1^, della 2^, dell'm-esima riga sono 1, 2, ..., m.
I numeri ai.k si chiamano elementi ed appartengono alla riga i-esima ed alla colonna k-esima.
Molte volte una matrice si indica con un'unica lettera A oppure con ai.k.
In particolare, se m = 1, si scrive:
a1, a2, ..., an,
tralasciando il puntino e l'indice in alto.
Se n = 1, si scrive:
tralasciando il puntino e l'indice in basso.
Se la matrice è formata da una riga e da una colonna, si eliminano entrambi gl'indici ed i puntini.
Le matrici si indicano anche scrivendo gl'indici entrambi in alto o entrambi in basso, dove il primo indice indica la riga ed il secondo la colonna:

Criterio del confronto per matrici dello stesso tipo
Date le matrici A e B dello stesso tipo (m, n):
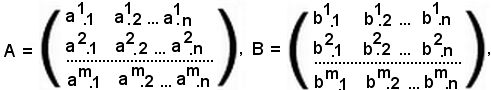
esse sono uguali se e solo se
cioè
A = B
In altri termini, le matrici A e B dello stesso tipo (m, n) sono uguali, se i termini che occupano lo stesso posto nelle matrici sono uguali.
Matrice nulla
Fra le matrici del tipo m x n vi è quella nella quale tutti gli elementi sono uguali a zero; tale matrice si indica con il simbolo Om,n, cioè
Om,n
Si esaminano ora alcuni argomenti necessari alla trattazione delle matrici.
Considerati n numeri, si effettua la loro somma
a1 + a2 + ... + an,
che si indica con
L'insieme dei valori che p assume si dice intervallo di variabilità degl'indici.
Considerati altri n numeri
b1, b2, ..., bn,
la seguente somma dei prodotti
a1b1 + a2b1 + ... + anb1
si indica con
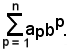
Supposto che gli n numeri b abbiano anche un indice fisso in basso:
b1.k, b2.k, ..., bn.k,
essi figurano nella colonna k-esima di una matrice.
Si considera ora la somma dei seguenti prodotti
a1b1.k + a2b2.k + ... + apbp.k,
e la si indica con
Dopo la seguente convenzione:
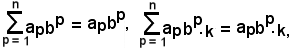
le suddette somme si possono scrivere in forme diverse esprimendo che, quando in un'espressione monomia si trovi un indice ripetuto in alto ed in basso, indice muto, di cui si conosca l'intervallo di variabilità, si somma rispetto a detto indice senza indicare il simbolo della sommatoria. Se occorre sommare rispetto a più indici ripetuti in alto ed in basso, indici muti, quando si conoscono i loro intervalli di variabilità, si usa la stessa convenzione:
Si suppone di avere n numeri reali e si dispongono in ordine crescente:
p1, p2, ..., pn,
con
p1 < p2 < ... < pn.
Tale allineamento si dice permutazione naturale.
Ogni altro allineamento
k1, k2, ..., kn
si dice permutazione in quanto, pur essendo gli stessi numeri, cambia l'ordine di allineamento.
Se si considerano due numeri di una permutazione, ki e ki, il cui primo sia minore del secondo, si ha
i < i.
Si dice che i due numeri ki e ki formano un'inversione se e solo se risulta
ki < ki.
Se il numero delle inversioni degli elementi di una permutazione è pari, la permutazione si dice di classe pari, se è dispari, la permutazione si dice di classe dispari.
Ci si pone la seguente domanda: quante sono le possibili permutazioni distinte, se è diverso l'ordine?
Si dimostra che il numero di permutazioni di n numeri è dato dal prodotto dei primi n numeri interi naturali
n(n - 1)(n - 2)...3·2·1
e si indica con n fattoriale, cioè:
n!
Tipi di matrici
-se m ≠ n, la matrice si dice rettangolare,
-se m = n, la matrice si dice quadrata; il numero n si chiama ordine della matrice quadrata e rappresenta il numero delle righe o delle colonne.
Nota bene
Non ha senso parlare di matrici rettangolari.
Struttura delle matrici

Determinanti delle matrici quadrate
Si considerino una matrice quadrata di ordine n ed una permutazione di n numeri:
i1, i2, ..., in;
tali permutazioni sono n!
Si indichi con i il numero delle inversioni che gli elementi della permutazione formano, si consideri il prodotto degli n fattori e si effettui la somma:
Si hanno tanti prodotti quante sono le permutazioni, la somma degli n fattoriale prodotti si chiama determinante della matrice A e si indica con
Il determinante di A è un numero, le righe e le colonne della matrice A si dicono righe e colonne del determinante di A.
Si calcola ora il determinante di una matrice A del 2° ordine:
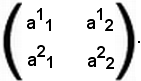
Si scrivono le permutazioni dei numeri 1 e 2:
1 e 2 non formano inversione, quindi i = 0,
2 ed 1 formano inversione, quindi i = 1.
Dunque:
|A| = (-1)0a11a22 + (-1)1a12a21 = a11a22 - a12a21.
Cioè, il determinante di una matrice quadrata del secondo ordine si ottiene effettuando la differenza dei prodotti fra gli elementi della diagonale principale e gli elementi della diagonale secondaria.
Si calcola anche il determinante di una matrice quadrata A del 3° ordine:

Si scrivono ora le permutazioni dei numeri 1, 2 e 3:
1 2 3 non formano inversioni, i = 0,
2 3 1 formano 2 inversioni, i = 2,
3 1 2 formano 2 inversioni, i = 2,
2 1 3 formano 1 inversione, i = 1,
1 3 2 formano 1 inversione, i = 1,
3 2 1 formano 3 inversioni, i = 3.
Dunque:
|A| = (-1)0a11a22a33 + (-1)2a12a23a31 + (-1)2a13a21a32 + (-1)1a12a21a33 + (-1)1a11a23a32 +
Tale calcolo si può effettuare anche scrivendo a destra, accanto al determinante della matrice A, le prime due colonne della stessa matrice e moltiplicando opportunamente gli elementi:

Cioè, dalle somme dei prodotti degli elementi delle diagonali rosse, si sottraggono i prodotti degli elementi delle diagonali celesti.
Si dimostra che:
-il determinante delle matrici di primo ordine è l'unico elemento della matrice A.
Infatti, si consideri la matrice
A = a11,
siccome i = 0, si ha
|A| = (-1)0a11 = a11.
Teorema 1
Si consideri la matrice

il cui determinante risulta
dove i rappresenta il numero delle inversioni.
Inoltre, si consideri la matrice B, ottenuta dalla matrice A moltiplicando gli elementi di una sua riga prefissata, ad esempio la prima, per uno stesso numero ρ, cioè

allora risulta
DetB = ρDetA.
E ciò ha senso per una matrice quadrata.
Definizione di trasposta di una matrice
Si consideri una qualsiasi matrice A del tipo (m, n), in particolare quadrata se m = n:

Si consideri ora la matrice, indicata con A-1, avente alla prima riga gli elementi della prima colonna ed alla prima colonna gli elementi della prima riga di A, alla seconda riga gli elementi della seconda colonna ed alla seconda colonna gli elementi della seconda riga di A, e così via, cioè:

Tale matrice, ottenuta scambiando le righe con le colonne, si chiama trasposta della matrice A, ed è del tipo (n, m).
Logicamente, se si considera la trasposta della trasposta di A, si ha la stessa matrice, cioè:
(A-1)-1 = A = aik,
con i = 1, 2, ..., m e k = 1, 2, ..., n.
Supponendo che la matrice sia quadrata, m = n, si dimostra che:
il determinante della matrice A è uguale al determinante della sua trasposta, cioè
DetA = DetA-1.
Da tale proposizione si deduce un principio di carattere generale:
-in ogni teorema sui determinanti si può scambiare la parola riga con la parola colonna, ottenendo un teorema altrettanto vero.
Teorema 2
Si consideri una matrice quadrata di ordine n:

Si consideri inoltre la matrice B, ottenuta da A scambiando di posto due righe prefissate, ad esempio le prime due, cioè:

Si dimostra che il determinante della matrice B è l'opposto del determinante della matrice A, cioè:
DetB = -DetA.
Se una matrice ha due righe uguali, il suo determinante è uguale a zero.
Si consideri la matrice
Si consideri ora la matrice, indicata con A-1, avente alla prima riga gli elementi della prima colonna ed alla prima colonna gli elementi della prima riga di A, alla seconda riga gli elementi della seconda colonna ed alla seconda colonna gli elementi della seconda riga di A, e così via, cioè:

Tale matrice, ottenuta scambiando le righe con le colonne, si chiama trasposta della matrice A, ed è del tipo (n, m).
Logicamente, se si considera la trasposta della trasposta di A, si ha la stessa matrice, cioè:
(A-1)-1 = A = aik,
con i = 1, 2, ..., m e k = 1, 2, ..., n.
Supponendo che la matrice sia quadrata, m = n, si dimostra che:
il determinante della matrice A è uguale al determinante della sua trasposta, cioè
DetA = DetA-1.
Da tale proposizione si deduce un principio di carattere generale:
-in ogni teorema sui determinanti si può scambiare la parola riga con la parola colonna, ottenendo un teorema altrettanto vero.
Teorema 2
Si consideri una matrice quadrata di ordine n:

Si consideri inoltre la matrice B, ottenuta da A scambiando di posto due righe prefissate, ad esempio le prime due, cioè:

Si dimostra che il determinante della matrice B è l'opposto del determinante della matrice A, cioè:
DetB = -DetA.
Se una matrice ha due righe uguali, il suo determinante è uguale a zero.

Si suppone che la riga r-esima sia uguale alla riga s-esima, cioè:
ar1 = as1, ar2 = as2, ..., arn = asn,
e ciò significa che
Si deve dimostrare che
DetA = 0.
Allo scopo, si consideri la matrice B ottenuta da A scambiando di posto la riga r-esima con l's-esima:

Per quanto visto in precedenza, risulta:
DetB = -DetA.
D'altronde, si sono scambiati elementi uguali e ciò non cambia nulla, pertanto
DetB = DetA,
quindi
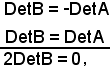
cioè
DetB = 0,
o anche
DetA = 0,
come volevasi dimostrare.
Si supponga di avere la matrice A quadrata di ordine n.
Si dice che la riga r-esima è proporzionale alla riga s-esima, se esiste ρ reale tale che
ar1 = ρas1, ar2 = ρas2, ..., arn = ρasn,
cioè
riga r-esima proporzionale alla riga s-esima
Si dimostra che se in una matrice vi sono due righe o due colonne proporzionali, il determinante è uguale a zero.
Si consideri la matrice

In tale matrice si è considerato
as1, as2, ..., asn
come elemento della riga r-esima, lasciando invariati gli altri.
Si osservi ora che la matrice A, ottenuta dalla matrice B moltiplicando tutti gli elementi della riga s-esima per ρ, è:

Per il teorema 1 si ha:
DetA = ρDetB,
inoltre la matrice A ha due righe uguali, pertanto
DetA = 0,
in definitiva
DetB = 0,
come volevasi dimostrare.
Si consideri la matrice

risulta

Ora, sia A una matrice qualsiasi di ordine n:
-si dice che la prima riga è combinazione lineare della seconda e della terza secondo i coefficienti λ e μ, se

Una riga può essere combinazione lineare di più righe:
a1k = λa2k + μa3k + δa4k.
Si dimostra che:
-se in una matrice una riga è combinazione lineare di altre righe, il determinante della matrice è uguale a zero.
Esempio
Si consideri la matrice

siccome la terza riga è combinazione lineare delle prime due secondo i coefficienti λ = 2 e μ = 1, si ha:

Si suppone di avere una matrice quadrata di ordine n, se agli elementi di una riga si aggiunge una combinazione lineare delle altre righe della matrice, il determinante della nuova matrice è uguale al determinante della matrice iniziale.

Cioè, si aggiunge alla terza riga una combinazione lineare della prima, della seconda e della quarta riga secondo i coefficienti λ, μ e δ:
a31 + λa11 + μa21 + δa41,
a32 + λa12 + μa22 + δa42,
a3n + λa1n + μa2n + δa4n.
Pertanto, il determinante di questa matrice è uguale al determinante della matrice inizialmente considerata.
Proprietà dei determinanti

Si suppone ora che ciascun elemento di una riga sia somma di due addendi, cioè si pone
a11 = c11 + b11, a12 = c12 + b12, a1k = c1k + b1k.
A tal punto, si considerano le due matrici ottenute sostituendo gli elementi della prima riga con i primi addendi e poi con i secondi addendi, cioè:
Si dimostra che:
DetA = DetB + DetC.
Esempio
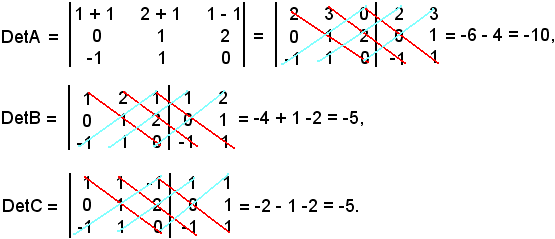
Quindi risulta
DetA = DetB + DetC = -5 - 5 = -10.
Calcolo di un determinante qualsiasi
Si consideri una matrice quadrata di ordine n:

Se si sopprimono la riga e la colonna a cui appartiene un generico elemento, ad esempio aik, i restanti elementi formano una nuova matrice quadrata di ordine n - 1:

Il determinante della matrice A' si chiama minore complementare dell'elemento aik, e si indica con
M.ki.
Si chiama complemento algebrico dell'elemento aik il minore complementare aik, preso con il proprio segno se la somma degl'indici aik è pari, mentre cambiato di segno se la somma degl'indici aik è dispari. Il complemento algebrico si indica come segue:
A.ki = (-1)i+kM.ki.
Si consideri la riga i-esima della matrice A, si dimostra che:
-la somma dei prodotti degli elementi della riga i-esima per i rispettivi complementi algebrici è uguale al determinante di A, cioè:
a|i|1A.1i + a|i|2A.2i + a|i|nA.ni = DetA,
oppure
Esempio 1)
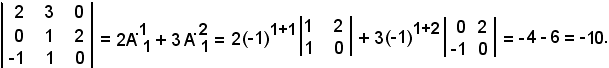
Esempio 2)
Sviluppando in base alla prima colonna

Considerando sempre lo stesso determinante, e sommando alla seconda colonna la quarta, si ha:

Si consideri una matrice

E' noto che lo sviluppo del determinante, secondo la linea i, è dato da
Si dimostra che la somma dei prodotti di una riga o colonna qualsiasi, per i rispettivi complementi algebrici degli elementi di un'altra riga j ≠ i, o colonna, è uguale a zero. Risulta cioè l'uguaglianza
aipApj = 0,
per j ≠ i.
In altri termini,
ai1A1j + ai2A2j + ... + ainAnj = 0.
Esempio
Si consideri la matrice

e si moltiplichi un elemento, ad esempio l'elemento 1, per il complemento algebrico del primo elemento della seconda riga:
Matrice inversa
Considerata una matrice quadrata di ordine n, si dice che è non singolare se il suo determinante è diverso da zero.
Si suppone che la matrice A sia non singolare, per cui sia
DetA = Δ ≠ 0.
Un elemento qualsiasi della matrice A, ad esempio aik, si chiama elemento reciproco dell'elemento preso in considerazione. Tale elemento reciproco è uguale al complemento algebrico di aik, diviso il determinante della matrice del complemento. In altri termini:
E' molto importante sapere che con i reciproci degli elementi di una matrice si può formare una nuova matrice nel seguente modo: innanzitutto si scrivono gli elementi reciproci degli elementi della prima colonna come prima riga, i reciproci degli elementi della seconda colonna come seconda riga, e così via.
La matrice così ottenuta si chiama inversa della matrice data e si indica con A-1.
Quindi l'inversa della matrice A è:
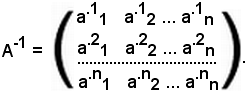
Esempio
Si consideri una matrice del terzo ordine:

Si verifica ora se tale matrice è non singolare.
Infatti, sviluppando gli elementi della seconda colonna si ha:
Δ = -1
ed il minore complementare
da cui
(-1)(-4) = 4.
Il primo elemento della prima riga è il reciproco di 1:
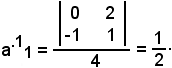
Il secondo elemento della prima riga è il reciproco di 2:
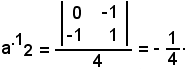
Il terzo elemento della prima riga è il reciproco di 1:
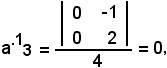
e così si procede fino ad ottenere tutti gli elementi della matrice inversa.
E' già noto che per definizione la trasposta della matrice A, indicata con A-1, è stata ottenuta scambiando nella matrice A le righe con le colonne:

Dalle nozioni di trasposta e di inversa di una data matrice si ha che, assegnata una matrice A non singolare, sia considerando prima l'inversa e poi la trasposta o viceversa, si ottiene la stessa matrice, cioè
(A-1)-1 = (A-1)-1.
Prima di dimostrare ciò, occorre prima osservare che, se si considera un elemento qualsiasi, ad esempio l'elemento aik della matrice A, esso è anche elemento della sua trasposta, inoltre il reciproco dell'elemento considerato coincide con il reciproco dello stesso elemento nella sua trasposta.
Infatti, sia data una matrice A di un certo ordine, ad esempio 3:

e si consideri la sua trasposta

Per un teorema precedente è noto che
DetA = DetA-1.
Pertanto, se si considera il reciproco di un elemento, ad esempio di a2.1 rispetto alla matrice A, si ha che a1.2 è uguale al complemento algebrico di a2.1 diviso il determinante di A, cioè
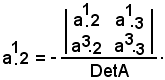
Ora, considerando il reciproco dello stesso elemento a2.1 rispetto alla trasposta della matrice A, si ha che a1.2 è uguale al complemento algebrico di a2.1 diviso il determinante di A-1, cioè
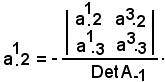
Dunque:
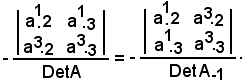
Osservato ciò, di conseguenza si dimostra che:
(A-1)-1 = (A-1)-1.
Infatti, effettuando la trasposta dell'inversa, si ha:

Inoltre, effettuando l'inversa della trasposta, si ha:

Dunque:
(A-1)-1 = (A-1)-1= A-1-1.
Di conseguenza, il reciproco dell'elemento aik si indica con aki, cioè
aik = aki.
(A-1)-1 = (A-1)-1= A-1-1.
Si considera ora la matrice A di ordine n scrivendo tutti gl'indici in basso:

Di conseguenza il reciproco dell'elemento aik si indica con aki, cioè
aik =aki.
Inoltre, si considera ora la matrice A di ordine n scrivendo tutti gl'indici in alto:


Di conseguenza il reciproco dell'elemento aik si indica con aki, cioè
aik =aki.
Inoltre, si considera ora la matrice A di ordine n scrivendo tutti gl'indici in alto:

Di conseguenza, il reciproco dell'elemento aik si indica con aki, cioè
aik = aki.
In precedenza si è visto che, considerata una matrice non singolare, risulta
a) DetA = a|i|.pA.pi,
inoltre è stato dimostrato che
ai.pA.pj = 0,
con i ≠ j.
Dividendo ambo i membri dell'uguaglianza a) per DetA, si ha:
essendo
Di conseguenza, nell'uguaglianza b) si ha:
essendo
Le uguaglianze
a|i|.p·a.pi = 1, a|i|.p·a.pj = 0
si possono conglobare in un'unica uguaglianza, introducendo il simbolo di Kronecher:
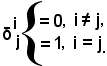
Usando tale simbolo, le due uguaglianze si possono anche scrivere:
ai.p·a.pj = δij.
Un'uguaglianza analoga si ottiene scambiando le righe con le colonne:
a.ip·ap.j = δij.
Prodotto di determinanti
Si considerino le matrici A e B dello stesso ordine:
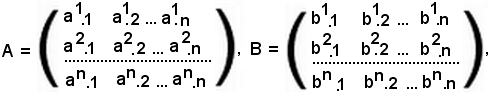
e si supponga che la matrice C sia il prodotto della matrice A per la matrice B

Quindi si ha:
A = ai.k, B = bi.k,
e sia
C = A·B.
Si ricordi inoltre che
con
p = 1, ..., n.
In particolare si consideri il prodotto della matrice A per l'inversa A-1:
A·A-1 = C.
Di conseguenza, l'elemento ci.k della matrice C risulta
ci.k = ai.pap.j.
Ma
ai.pap.j = δij,
quindi
ci.j = ai.pap.j = δij.0.
Scrivendo per esteso, si ha:

Tutti gli elementi che hanno indici distinti sono uguali a zero, mentre quelli che hanno indici uguali sono uguali ad 1.
Questa matrice si chiama matrice unità.
Ovviamente, la matrice unità è uguale alla matrice A per la sua inversa.
Essendo
DetC = DetA·DetB,
applicando tale proprietà, si ha:

Per tale motivo risulta
DetU = DetA·DetA-1.
Pertanto
Si è quindi ottenuto
DetA·DetA-1 = 1,
da cui
Di conseguenza, essendo A non singolare, risulta
Si è quindi stabilito che l'inversa della matrice A è diversa da zero, cioè
A-1 ≠ 0,
e quindi è anch'essa non singolare; inoltre, il determinante dell'inversa di una matrice è uguale all'inverso del determinante della matrice assegnata.
Teorema 3
Si consideri la matrice

si supponga inoltre che il determinante della matrice A sia uguale a zero.
Si dimostra che esiste una sola riga, o colonna, della matrice A che è combinazione lineare di altre righe, o colonne, della stessa matrice.
Infatti, se il determinante della matrice A è uguale a zero, vuol dire che esiste una combinazione lineare nulla delle righe della matrice a coefficienti non tutti nulli, cioè che esiste una riga, ad esempio la prima, che sia combinazione lineare delle altre due.
Quindi, esistono n coefficienti tali che:
λ1a11 + λ2a21 + ... + λnan1 = 0,
λ1a12 + λ2a22 + ... + λnan2 = 0,
λ1a1n + λ2a2n + ... + λnann = 0.
Rango di una matrice
Si consideri una matrice A del tipo (m, n), diversa dalla matrice nulla:


Si consideri inoltre un numero intero positivo p tale che
1 ≤ p ≤ m, 1 ≤ p ≤ n.
A tal punto, si fissano arbitrariamente p righe e p colonne; gli elementi comuni a queste p righe e p colonne formano una matrice quadrata che si chiama matrice estratta dalla matrice A.
Si suppone ora p = 2 e si scelgono, ad esempio, come righe la prima e la terza, e come colonne la seconda e l'ultima. Gli elementi comuni, come è indicato in 1), formano la seguente matrice:
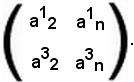
Di queste matrici ve ne sono molte, inoltre i determinanti estratti si chiamano determinanti estratti dalla matrice A.
Si dice che il numero ρ ≥ 1 è il rango o la caratteristica della matrice A se e solo se tra i determinanti estratti di ordine ρ ne esiste uno diverso da zero, e tutti i determinanti di ordine maggiore di ρ, se esistono, sono uguali a zero.
Nota bene
1)-ρ è il massimo intero positivo per cui esiste qualche determinante;
2)-se A = Om,n, per convenzione si dice che il rango della matrice A è uguale a zero, cioè per convenzione si assume rango zero per una matrice avente elementi nulli;
3)-se una matrice non è nulla, il suo rango è diverso da zero.
Si dimostra che:
-il rango di una matrice è uguale al rango della sua trasposta.
Infatti, la trasposta della matrice A è la matrice A-1, ottenuta scambiando le righe con le colonne. Allora le matrici estratte dalla trasposta di A saranno le trasposte delle matrici estratte da A. Si suppone, infatti, di fissare p righe e p colonne in A; si osserva che nella trasposta di A le righe diventano colonne. Dunque, gli elementi che appartengono alle colonne di A appartengono alle righe di A-1, e viceversa:
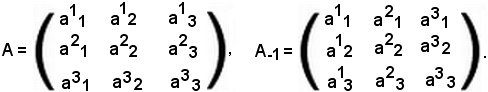
Si indichino ora con B e B-1 le matrici estratte rispettivamente da A ed A-1:
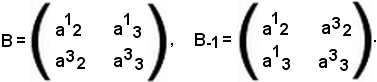
E' noto che i determinanti di due matrici quadrate, l'una trasposta dell'altra, sono uguali, allora i determinanti estratti dalla matrice A sono uguali a quelli estratti dalla trasposta di A, cioè:
DetB = DetB-1.
Se i determinanti sono gli stessi, anche il rango è lo stesso, esempio:

La terza riga è combinazione lineare delle prime due.
Si consideri un qualsiasi determinante del terzo ordine estratto dalla matrice A, anche in tal caso la terza riga è combinazione lineare delle prime due, dunque il determinante del terzo ordine è uguale a zero, e ciò accade sempre, per cui il rango non può essere uguale a tre:

C'è però almeno un determinante del secondo ordine estratto dalla matrice A, diverso da zero, per cui il rango è uguale a due:
Considerata la matrice

il rango di una matrice non singolare di ordine n è uguale ad n.
Sistemi
Si consideri un sistema del tipo seguente:
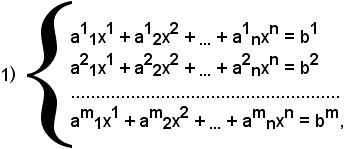
dove x1, x2, x3, ..., xn sono incognite,
a1pxp = b1 si somma per p = 1, 2, ..., n,
a11, a12, a13, ..., a1n sono reali o complessi.
Un sistema di questo tipo si chiama sistema lineare, di primo grado, di m equazioni in n incognite. Gli aik si chiamano coefficienti del sistema. I termini b1, b2, ..., bm si chiamano termini noti.
Per soluzione del sistema s'intende un'enupla di numeri
x10, x20, ..., xn0
che, sostituiti alle variabili, soddisfano il sistema.
Se il sistema ammette una soluzione si dice compatibile, se non ammette una soluzione si dice incompatibile.
Se tutti i termini noti sono uguali a zero, il sistema si dice omogeneo.
Si dimostra che tutti i sistemi omogenei sono compatibili.
Infatti, supponendo che l'enupla di numeri
x10, x20, ..., xn0
sia uguale a zero, cioè tale che
x1 = 0, x2 = 0, ..., xn = 0,
si ha una soluzione nulla o banale.
Il numero delle equazioni è uguale al numero delle incognite.
Nel caso in cui m = n si ottiene un sistema lineare omogeneo di n equazioni in n incognite. Con i coefficienti di questo sistema, si può formare una matrice quadrata di ordine n data da

Tale matrice si chiama matrice dei coefficienti del sistema.
Si dimostra che:
A non singolare
Si consideri un sistema lineare di n equazioni in n incognite non omogeneo, e sia A la matrice dei coefficienti. Se la matrice è non singolare, il sistema ammette una ed una sola soluzione, e questa si calcola, ad esempio, con la regola di Cramer.
Si procede come segue:
si considera la prima incognita uguale ad una frazione avente per numeratore il determinante della matrice ottenuta da A, sostituendo alla prima colonna quella dei termini noti.

Esempio
Si consideri il seguente sistema non omogeneo
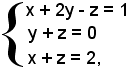
e sia A la matrice dei coefficienti:

Si calcola ora il determinante di tale matrice:

Quindi:
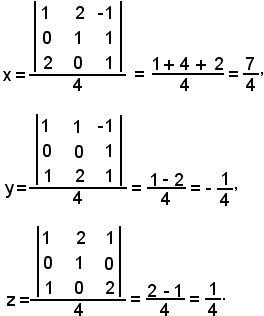
Teorema di Rouché Capelli
Tale teorema permette di stabilire se un qualsiasi sistema lineare è compatibile.
Si consideri un sistema lineare di m equazioni in n incognite:
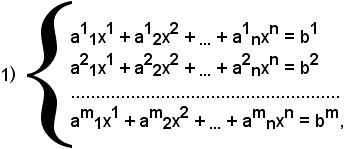
e si costruisca la matrice A dei coefficienti delle equazioni e la matrice B dei coefficienti e dei termini noti.
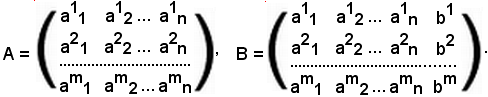
Condizione necessaria e sufficiente affinchè il sistema sia compatibile, è che le matrici A e B abbiano lo stesso rango.
Tale teorema vale anche quando il sistema è omogeneo.
Infatti, se i termini noti sono tutti nulli, allora le matrici estratte da A sono anche estratte da B, ma alcune matrici estratte da B, quelle contenenti la colonna nulla, non sono estratte da A, e ciò è interessante perchè il determinante di tali matrici è uguale a zero.
Dunque, anche in tal caso A e B hanno lo stesso rango.
Il teorema ora visto assicura l'esistenza delle soluzioni, però per trovarle si adotta il metodo seguente.
Si supponga che A e B abbiano lo stesso rango, che è detto rango del sistema. Si consideri inoltre il determinante di ordine ρ, estratto da A e diverso da zero, che si suppone essere formato dalle prime ρ righe e ρ colonne della matrice A, cioè:

Si consideri ora il sistema formato dalle ρ equazioni, i cui coefficienti figurano nel determinante suddetto:
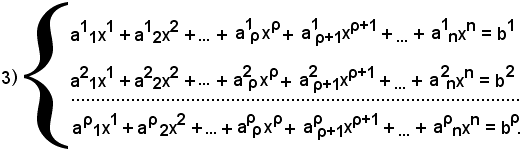
Si dimostra che il sistema 1) di m equazioni è equivalente al sistema 3) di ρ equazioni, in tal modo sono state scartate m - ρ equazioni e nel determinante 2) si avranno i coefficienti di ρ incognite.
Si considerano ora le m - ρ incognite (cioè xρ+1, xρ+2, xn), i cui coefficienti non figurano in tale determinante, e si considerano le seguenti posizioni:
xρ+1 = kρ+1, xρ+2 = kρ+2, xn = kn,
con kρ+1, kρ+2, kn numeri arbitrari.
Tali numeri si sostituiscono nel sistema 3) e si ottiene il seguente sistema 4):
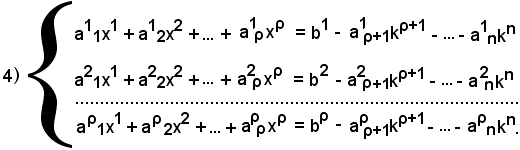
Si è così ottenuto un sistema di ρ equazioni in ρ incognite, la cui matrice dei coefficienti è nota, ed il cui determinante è il 2), ed è diverso da zero. Il sistema 4), essendo di ρ equazioni in ρ incognite, ammette una ed una sola soluzione e si risolve con la regola di Cramer.
Evidentemente, la soluzione dipende dal valore arbitrario di k, ad ogni modo comunque si fissa k si ha un'unica soluzione:
ed al loro variare, si hanno varie soluzioni del sistema.
Si può quindi asserire che
sono le generiche soluzioni del sistema 1).
Si osserva che

Si fissano dunque m - ρ in infiniti modi; si dice che il sistema ammette infinito m - ρ soluzioni.
Esempio 1): sistema di quattro equazioni in due incognite.
Per vedere se tale sistema è compatibile, si considera la matrice A dei coefficienti, che è del tipo (4, 2), e la matrice B, che è del tipo (4, 3), dei coefficienti delle incognite e dei termini noti:
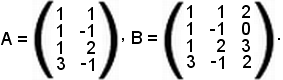
Il rango della matrice A è uguale a due, poichè esiste un estratto del secondo ordine il cui determinante è diverso da zero. Il rango della matrice B è uguale a due e non a tre, poichè i determinanti degli estratti del terzo ordine sono tutti uguali a zero, essendo la terza colonna combinazione lineare delle altre due; il rango non può essere minore di due, poichè gli estratti da A sono uguali a quelli di B e dunque, essendo due il rango di A, tale è quello di B. Si considera ora il seguente determinante del secondo ordine estratto da A
e si considerano le equazioni, i cui coefficienti figurano nel determinante ora scelto:
tale sistema equivale a quello iniziale e quest'ultimo si risolve con la regola di Cramer.
Esempio 2): sistema di tre equazioni in tre incognite.
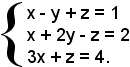
Si considera prima la matrice A dei coefficienti e poi la matrice B dei coefficienti delle incognite e dei termini noti:
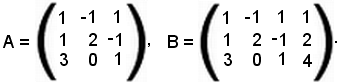
Il determinante della matrice A è uguale a zero, poichè la terza riga è combinazione lineare delle altre due, dunque il rango non è tre ma due, poichè esiste qualche determinante del secondo ordine estratto da A che è diverso da zero. Anche il rango della matrice B non è uguale a tre, poichè la terza riga è combinazione lineare delle altre due, dunque il rango è due.
Il sistema dato è quindi compatibile, ed ammette infinito ad uno soluzioni.
Si fissa ad arbitrio il valore di un'incognita e si considera un determinante di ordine due diverso da zero, estratto dalla matrice A:
Dunque, si scrivono le ultime due equazioni:
il cui sistema è equivalente a quello iniziale.
Ponendo
x = k,
si ha:
Sommando membro a membro, risulta:
2y - z + z = 2 - k + 4 - 3k,
o anche
2y = 6 - 4k,
da cui
y = 3 - 2k.
Quindi la soluzione del sistema è
x = k, y = 3 - 2k, z = 4 - 3k.
Si vuol vedere ora se un sistema omogeneo ammette soluzione diversa da quella banale; a tal fine sussiste il seguente teorema.
Teorema
Condizione necessaria e sufficiente affinchè un sistema lineare omogeneo di m equazioni in n incognite ammetta soluzioni diverse da quella banale, è che la matrice dei coefficienti abbia rango minore del numero delle incognite.
Le radici si trovano allo stesso modo dei sistemi lineari non omogenei.
Esempio: si consideri il seguente sistema lineare omogeneo di tre equazioni in tre incognite.
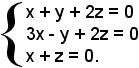
Per trovare le soluzioni si considera la matrice dei coefficienti dell'equazione:

Essendo il determinante di tale matrice uguale a zero, il rango della matrice dei coefficienti non può essere tre ma è due, perchè il determinante estratto è diverso da zero, cioè:
Dunque, il sistema ammette una soluzione diversa da quella banale perchè il rango è minore del numero delle incognite.
Si considerano ora le equazioni i cui coefficienti figurano nel minore estratto della matrice dei coefficienti:
Ponendo
x = k,
si ha:
Il sistema ha dunque la soluzione generale
x = k, y = k, z = -k.
Se si dà a k il valore zero, si ha la soluzione banale; se si dà a k un valore diverso da zero, si ha la soluzione non banale.
Per risolvere un sistema omogeneo si usa un altro metodo, però prima si osserva quanto segue.
Si suppone che
x10 x20 ... xn0
sia una soluzione di un sistema omogeneo, λ un numero complesso ed inoltre si consideri la seguente enupla
Si dimostra che anche l'enupla
è una soluzione del sistema.
Allo scopo, è sufficiente dimostrare che
Infatti:
Si vede ora un altro metodo per risolvere particolari sistemi omogenei.
Si considera un sistema omogeneo di n-1 equazioni in n incognite:
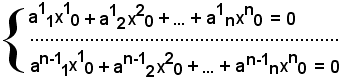
e si suppone che il rango della matrice dei coefficienti sia n-1. Per tale motivo, il sistema ammette soluzioni non banali, inoltre per trovare le soluzioni del sistema si procede come segue.
Allo scopo, si considera la matrice dei coefficienti del sistema:

Si assume per x1 il determinante estratto dalla matrice dei coefficienti, sopprimendo la prima colonna; per x2 il determinante estratto dalla matrice data, sopprimendo la seconda colonna; e così via:
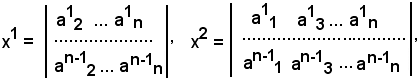
e per un generico p
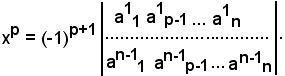
In tal modo, il sistema ammette una sola soluzione, per ottenerle tutte basta moltiplicare i determinanti estratti per un parametro k.
Esempio: si consideri il seguente sistema lineare omogeneo di tre equazioni in tre incognite.
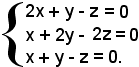
Il determinante dei coefficienti dell'equazione è uguale a zero, cioè:
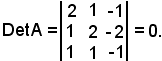
Infatti, moltiplicando la terza riga per 3, si ha:
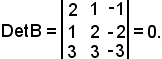
Siccome
DetB = 3DetA,
si ha
3DetA = 0,
cioè
DetA = 0.
Dunque, il rango di A non è 3 ma 2, in quanto esiste il determinante
estratto da A, che è diverso da zero.
Il sistema iniziale è dunque equivalente al seguente:
che è a due equazioni e tre incognite.
Tale sistema si risolve con il metodo espresso in precedenza e si ha:
In definitiva, le soluzioni sono date da:
x = 0, y = 3k, z = 3k.
Si suppone ora di avere un sistema lineare omogeneo di m equazioni in n incognite e sia m < n. Ci si chiede se tale sistema ammette soluzioni diverse da quella banale.
Infatti, affinchè ammetta soluzioni diverse da quella banale, occorre che il rango della matrice dei coefficienti sia minore del numero delle incognite.
In tal caso il rango ρ non si conosce, ma è noto che ρ ≤ m, e poichè m < n , si ha ρ ≤ n.
Se ρ ≤ n, allora il sistema ammette certamente soluzioni diverse da quella banale.
A completamento dello studio delle matrici, si richiamano concetti già visti e si forniscono ulteriori definizioni ed esempi.
Prodotto fra numeri complessi e matrici
Sia ρ un numero complesso, cioè ρ
Per prodotto del numero complesso ρ per la matrice A s'intende la matrice ottenuta moltiplicando tutti gli elementi della matrice A per ρ; essa si indica con ρA e risulta:
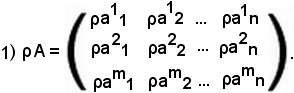
Se per caso la matrice A è quadrata di ordine n, cioè A(n, n), anche la matrice prodotto ρA è dello stesso ordine e si ha:
2) DetρA = ρnDetA.
Per stabilire tale relazione, si procede come segue. Si indica con DetρA il determinante della matrice prodotto di ρ con A, e con DetA il determinante della matrice A, pertanto risulta:
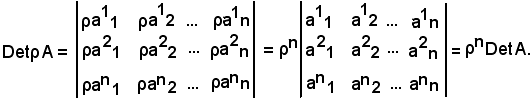
Quindi si ha:
DetρA = ρnDetA.
Esempio
Siano assegnati
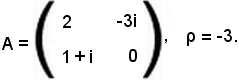
La matrice prodotto risulta
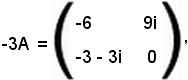
quindi,
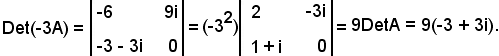
In generale vale anche la seguente uguaglianza
ρA = Aρ,
in cui Aρ è espresso come segue:
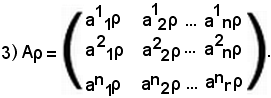
Le matrici 1) e 3) sono uguali perchè godono della proprietà commutativa:
ρaik = aikρ,
e ciò perchè anche il prodotto di due numeri complessi gode della proprietà commutativa.
Infatti, siano
ρA = Aρ,
in cui Aρ è espresso come segue:
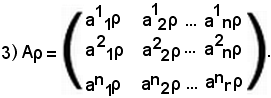
Le matrici 1) e 3) sono uguali perchè godono della proprietà commutativa:
ρaik = aikρ,
e ciò perchè anche il prodotto di due numeri complessi gode della proprietà commutativa.
Infatti, siano
A = aik, ρA = ρaik, Aρ = aikρ,
ed essendo
ρA = Aρ,
risulta anche
ρaik = aikρ.
Matrici somma di due matrici
Si considerino le seguenti due matrici del tipo (m, n):
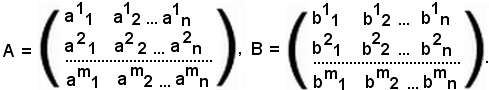
A
tal punto si può definire una nuova matrice in cui gli elementi sono
ottenuti sommando gli elementi che occupano lo stesso posto in entrambe
le matrici:
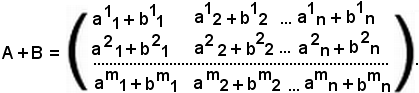
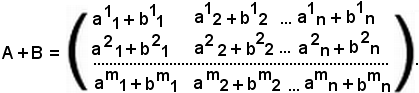
Questa matrice prende il nome di matrice somma ed è dello stesso ordine delle matrici A e B.
Se
A = aik, B = bik,
con
i = 1, 2, ..., m e k = 1, 2, ..., n,
la matrice somma è espressa da
A + B = aik + bik.
Se si considera la matrice B + A, si ha:
B + A = bik + aik.
Le matrici A + B e B + A hanno gli elementi comuni uguali e pertanto, essendo
aik + bik = bik + aik,
risulta
A + B = B + A.
Ciò conferma che anche le matrici godono della proprietà commutativa.
Si consideri ora un'ulteriore matrice
C = cik,
si asserisce che le matrici godono della proprietà associativa:
(A + B) + C = A + (B + C).
Essendo
(A + B) + C = (aik + bik) + cik,
A + (B + C) = aik + (bik + cik),
risulta
(aik + bik) + cik = aik + (bik + cik),
quindi le nuove matrici sono:
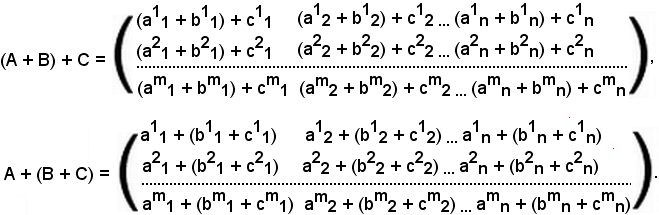
Si considerino tre matrici del tipo (m, n):
A = aik, B = bik, C = cik,
e siano inoltre λ, μ, δ tre numeri complessi.
Si possono ora considerare le matrici e le combinazioni lineari di A, B, C secondo λ, μ e δ:
λA = λaik, μB = μbik, δC = δcik,
cioè
λA + μB + δC = λaik + μbik + δcik.
Esempio
Si considerano due matrici del tipo (2, 3)
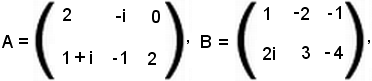
si ha:
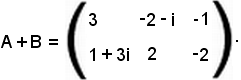
Fra le matrici del tipo (m, n), si considerino tutte quelle che hanno i = 0; indicando tale matrice con zero, si ha:

Se a tale matrice si somma una matrice A del tipo (m, n), si ha:
A + 0 = A = 0 + A.
Se si ha una matrice A, si può determinare una matrice X dello stesso tipo, tale che:
A + X = 0, X = -A,
quindi risulta anche
aik + xik = 0, xik = -aik,
essendo
A = aik, X = xik.
In tal caso, gli elementi della matrice X sono opposti a quelli della matrice A.
Siano A una matrice del tipo (m, n), α e β due numeri complessi. Siccome α·β è un numero complesso, si può sempre considerare la matrice A per α·β, cioè:
1) (α·β)A = α(βA) = β(αA) = αβA.
Se A ha aik elementi, il generico elemento della matrice (α·β)A è (αβ)aik per ogni i = 1, 2, ..., m e k = 1, 2, ..., n, pertanto si ha:
2) (αβ)aik = α(βaik) = β(αaik).
Nelle uguaglianze 1) e 2), come si può notare, valgono sempre le proprietà commutativa ed associativa.
Inoltre, si può parlare della proprietà distributiva della somma rispetto al prodotto.
Siano A e B due matrici del tipo (m, n),
A = aik, B = bik,
con i = 1, 2, ..., m e k = 1, 2, ..., n, ed α un numero complesso.
Si considerino ora la matrice somma A + B e la matrice prodotto α(A + B).
Si dimostra che
3) α(A + B) = αA + αB = Aα + Bα = (A + B)α,
e che quindi la proprietà distributiva vale sia a destra che a sinistra.
Rispetto alla i-esima riga ed alla k-esima colonna, la matrice α(A + B) ha rispettivamente i seguenti elementi:
α(aik + bik),
mentre i corrispondenti elementi delle matrici αA ed αB sono:
αaik + αbik.
Analogamente alla 3), si ha:
α(aik + bik) = αaik + αbik = aikα + bikα = (aik + bik)α.
Se A e B sono matrici quadrate dello stesso ordine, la matrice somma A + B è sempre una matrice quadrata dello stesso ordine. In generale, risulta:
Det(A + B) ≠ DetA + DetB.
Si considerino una matrice A del tipo (h, m) ed una matrice B del tipo (m, l) e si faccia in modo che il numero delle colonne di A sia uguale al numero delle righe di B:
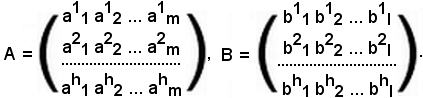
Quindi,
fissata una riga di A ed una colonna di B, il numero degli elementi di
una riga di A è uguale al numero degli elementi di una colonna di
B. Indicando con p la riga di A e con q la colonna di B, si
consideri della matrice B la q-esima e la somma degli elementi della p-esima di A per la q-esima di B; quindi risulta:
cpq = apibiq
per ogni p = 1, 2, ..., h e q = 1, 2, ..., l.
Si può considerare quindi la matrice C del tipo (h, l) i cui elementi sono i numeri cpq definiti come sopra.
Tale matrice si chiama matrice prodotto linee per colonne della matrice A per la matrice B e si indica nell'ordine AB.
Esempio
Si considerino le matrici A del tipo (2, 3) e B del tipo (3, 1):
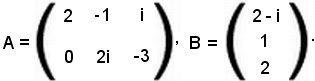
cpq = apibiq
per ogni p = 1, 2, ..., h e q = 1, 2, ..., l.
Si può considerare quindi la matrice C del tipo (h, l) i cui elementi sono i numeri cpq definiti come sopra.
Tale matrice si chiama matrice prodotto linee per colonne della matrice A per la matrice B e si indica nell'ordine AB.
Esempio
Si considerino le matrici A del tipo (2, 3) e B del tipo (3, 1):
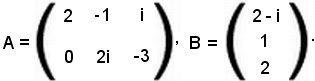
La matrice prodotto AB è del tipo (2, 1), cioè
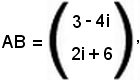
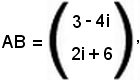
c11 = 4 - 2i - 2i - 1 = 3 - 4i, c21 = 2i + 6.
Si consideri ora il caso in cui la matrice A sia del tipo (h, m) e la matrice B del tipo (m, h) e si indichi con AB una matrice di ordine h, cioè del tipo (h, h), e con BA una matrice di ordine m, cioè del tipo (m, m), con h ≠ m; pertanto, risulta
AB ≠ BA.
Si osserva che se h = m, AB e BA sono matrici di ordine m; inoltre, risulta:
AB = apibiq,
BA = bpiaiq,
e poichè
AB = BA,
si ha:
apibiq = bpiaiq.
Quindi, in generale, si può dire che il prodotto gode della proprietà commutativa.
Esempio
Si considerino le matrici A del tipo (2, 3) e B del tipo (3, 1):
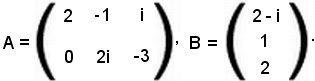
La matrice prodotto AB è del tipo (2, 1), cioè
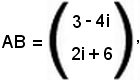
in cui
c11 = 4 - 2i - 2i - 1 = 3 - 4i, c21 = 2i + 6.
Si consideri ora il caso in cui la matrice A sia del tipo (h, m) e la matrice B del tipo (m, h), e si indichi con AB una matrice di ordine h, cioè del tipo (h, h), e con BA una matrice di ordine m, cioè del tipo (m, m), con h ≠ m; pertanto, risulta
AB ≠ BA.
Si osserva che se h = m, AB e BA sono matrici di ordine m; inoltre, risulta:
AB = apibiq,
BA = bpiaiq,
e poichè
AB = BA,
si ha:
apibiq = bpiaiq.
Quindi, in generale, si può dire che il prodotto gode della proprietà commutativa.
Esempio
Si considerino le seguenti matrici:
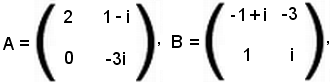
la matrice prodotto AB risulta
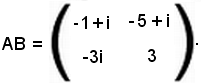
In tale matrice gli elementi della prima riga sono stati calcolati come segue:
1° elemento: 2(-1 + i) + 1 - i = -2 + 2i + 1 - i = -1 + i;
2° elemento: -6 + (1 - i) = -6 + 1 + i = -5 + i.
Gli elementi della seconda riga sono: -3i e 3.
Inoltre, la matrice prodotto BA risulta
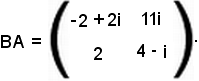
In tale matrice gli elementi della prima e della seconda riga sono stati calcolati come segue:
1° elemento della prima riga: 2(-1 + i) + 0 = -2 + 2i;
2° elemento della prima riga: 11i;
1° elemento della seconda riga: 2;
2° elemento della seconda riga: 4 - i.
Si calcolano ora i seguenti determinanti:
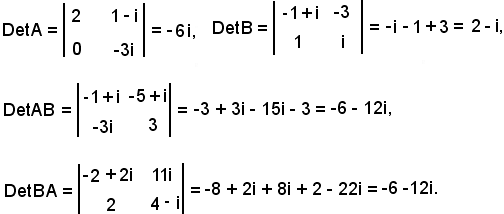
In tal modo è dimostrato che:
DetAB = DetBA.
Si considerino tre matrici A, B, C rispettivamente di termini generici aik, bik, cik e di tipo (h, m), (m, l), (l, s), cioè
A = aik, B = bik, C = cik.
Tali matrici godono delle proprietà distributiva, commutativa e associativa.
Pertanto si consideri
1) (AB)C = (apibiq)cqt,
di tipo (h, s); t si chiama indice muto.
2) A(BC) = apj(biqcqt),
di tipo (h, s); j si chiama indice muto.
Applicando la proprietà distributiva alla 2), si ha:
apj(biqcqt) = apjbiqcqt,
e quindi
(AB)C = A(BC) = ABC.
Proprietà delle matrici
Considerate due matrici
A = aik, B = bst,
rispettivamente di tipo (h, m) ed (m, l), si può definire la matrice
AB = cpq = cpqbiq,
che è di tipo (h, l).
Si considerino inoltre un numero complesso α e la matrice prodotto di α per AB; si dimostra quanto segue:
α(AB) = (αA)B = A(αB).
Basta dimostrare che gli elementi della matrice α(AB) sono uguali a quelli della matrice (αA)B che, rispetto alla p-esima ed alla q-esima colonna, hanno elementi
αcpq = α(apibiq),
dove quest'ultimi sono numeri complessi e godono della proprietà distributiva, pertanto si ha:
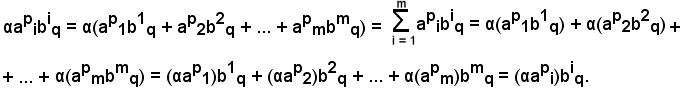
Quest'ultimo elemento è quello corrispondente della matrice (αA)B e tale uguaglianza dimostra che
α(AB) = (αA)B.
Analogamente, si dimostra che
α(AB) = A(αB).
Pertanto, per le proprietà commutativa e associativa dei numeri complessi:
α(apibiq) = api(αbip).
Si considerino tre matrici A, B, C rispettivamente di termini generici aik, bst, cst e di tipo (h, m), (m, l), (m, l), cioè
A = aik, B = bst, C = cst.
Si può parlare di matrice somma del tipo (m, l), cioè
B + C = bst + cst.
Si dimostra che
A(B + C) = AB + AC,
cioè che vale la proprietà distributiva a sinistra.
Si considerano gli elementi generici
api(biq + ciq),
che rappresentano numeri complessi, quindi fissato i si può considerare la somma dei prodotti. Applicando la proprietà distributiva, si può considerare:
api(biq + ciq) = apibiq + apiciq.
D'altronde
api(biq + ciq) = ap1(b1q + c1q) + ap2(b2q + c2q) + ... = ap1b1q + ap1c1q + ap2b2q + ap2c2q +
+ ... = ap1b1q + ap2b2q + ap1c1q + ap2c2q + ... = apibiq + apiciq.
apiciq è il termine corrispondente in AC, apibiq è il termine corrispondente in AB, quindi:
A(B + C) = AB + AC.
Analogamente, se si considerano tre matrici A, B, C rispettivamente di termini generici aik, bik, cst di tipo (h, m), (h, m), (m, l), cioè
A = aik, B = bik, C = cst,
si può parlare di matrice somma A + B del tipo (h, m) e si può considerare la proprietà distributiva a destra, cioè
(A + B)C = AC + BC.
La dimostrazione è analoga alla precedente.
Matrice unità
Si considera una matrice quadrata di ordine n, indicata con U, e si indicano con δki i suoi elementi con i, k = 1, 2, ... n. Quindi
U = δki.
I simboli δki si chiamano simboli di Kronecker e sono così definiti:
δki = 0, i ≠ k,
δki = 0, i ≠ k,
δki = 1, i = k.
La matrice ha gli elementi della diagonale principale uguali ad uno e quelli della diagonale secondaria uguali a zero, e prende il nome di matrice unità:
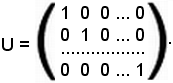
Logicamente, essa è sempre di ordine n.
Se A = aik è una matrice del tipo (m, n), ed U è di ordine n, si può considerare la matrice
AU = A,
che è sempre di ordine n. Gli elementi generici sono:
apiδiq = apq.
A tal punto, si asserisce che i termini corrispondenti di due matrici sono uguali.
Si osserva che se m ≠ n, non si può parlare di matrice prodotto AU.
Siano U una matrice unità e B un'altra matrice del tipo (n, m), allora UB è del tipo (n, m) e si dimostra che
UB = B e δpi = biq
e sarà
δqi = 0 se i ≠ q,
δqi = 1 se i = q.
Si osserva che se m ≠ n, non si può parlare di matrice prodotto UB.
Si suppone ora che A sia una matrice quadrata di ordine n ed U la matrice unità:
AU = A, UA = A,
cioè le matrici A ed U sono permutabili.
Siano A e B due matrici dello stesso tipo (h, l) e si consideri la trasposta (AB)-1; si dimostra che
essa è uguale alle trasposte di B-1A-1, cioè:
(AB)-1 = B-1A-1.
Data una matrice quadrata di ordine n, essa è non singolare se il suo rango è diverso da zero. Di tale matrice si può parlare dell'inversa A-1. Se gli elementi di A sono aik, i reciproci sono aki e sono così definiti:
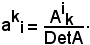
E' stato dimostrato che
apiaiq = δpq,
δpq = 0 se p ≠ q,
δpq = 1 se p ≠ q,
allora si deduce che
AA-1 = U = A-1A.
Si dimostra ora che
(A-1)-1 = A.
Infatti, siccome è noto che
A-1(A-1)-1 = U,
moltiplicando a sinistra per A, risulta
AA-1(A-1)-1 = AU (AA-1)(A-1)-1= A
(AA-1)(A-1)-1= A  U(A-1)-1= A
U(A-1)-1= A  (A-1)-1= A.
(A-1)-1= A.
Data la matrice A non singolare, si considera la sua trasposta, che è anch'essa non singolare. A tal punto, si considera l'inversa della trasposta (A-1)-1 e si dimostra che
(A-1)-1 = (A-1)-1,
cioè la trasposta e l'inversa sono permutabili e si usa il simbolo
A-1-1.
Si dimostra che se A e B sono due matrici quadrate non singolari di ordine n, considerata la matrice prodotto AB, anche questa è non singolare e l'inversa di AB è uguale al prodotto dell'inversa di B per l'inversa di A, cioè:
(AB)-1= B-1A-1.
Infatti, dalla proprietà
AA-1 = U
si deduce che
(AB)-1(AB) = U (AB)-1(AB)B-1 = UB-1
(AB)-1(AB)B-1 = UB-1  (AB)-1A(BB-1) = B-1
(AB)-1A(BB-1) = B-1  (AB)-1A = B-1
(AB)-1A = B-1 
 (AB)-1(AA-1) = B-1A-1
(AB)-1(AA-1) = B-1A-1  (AB)-1 = B-1A-1.
(AB)-1 = B-1A-1.
Siano T una matrice non singolare di ordine n ed A una matrice quadrata dello stesso ordine.
Si dice trasformata di A mediante T, e si indica con TA, la matrice
TAT-1.
Si dimostra che
DetA = DetTAT-1.
Si dimostra ora che se A e B sono due matrici quadrate di ordine n, considerato il prodotto AB, la trasformata di AB è uguale al prodotto della trasformata di A per la trasformata di B, cioè
T(A B) = TATB.
Infatti, tenendo conto che U = T-1T, si ha:
T(A B) = TAABT-1 = TAAUBT-1 = (TAAT-1)(TBT-1)= TATB.
Siano A una matrice quadrata di ordine n ed U la matrice unità. Si considera ora la matrice
A - ρU,
con ρ indeterminato. Di tale matrice quadrata si considera il determinante, ottenendo così un polinomio nell'indeterminata ρ di grado n, che si chiama polinomio caratteristica di ρ.
Essendo
A = aik, U = δik,
l'elemento generico di A - ρU è
aik - ρδik.
La matrice è dunque
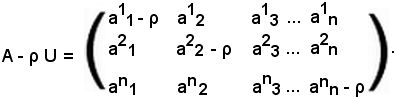
Il determinante
Det(A - ρU) = U
è l'equazione caratteristica.
Siano T una matrice quadrata non singolare ed A un'altra matrice; si consideri inoltre la trasformata di T mediante A,TA = TAT-1. Se al posto della matrice A si considera la matrice A - ρU, si ha:
TA - ρU = T(A - ρU)T-1 = (TA - TρU)T-1 = (TA - ρTU)T-1 = TAT-1- ρTUT-1= TA - ρU.
Considerando
DetTA = Det(TA - ρU) = Det(A - ρU),
si ha che il polinomio della matrice A trasformata mediante T, cioè Det(TA - ρU), è uguale a Det(A - ρU), polinomio caratteristico della matrice A.
Matrice ortogonale
Sia A una matrice quadrata di ordine n, si dice che A è una matrice ortogonale se il prodotto con la sua trasformata è uguale alla matrice unità di ordine n, cioè
A = aik, AA-1 = U.
Matrice simmetrica
Una matrice A = aik si dice simmetrica se
aik = aki,
cioè i termini simmetrici sono uguali.
Una matrice simmetrica è uguale alla sua trasposta.
Dalla proprietà
(A-1)-1= A
nel caso di una matrice non singolare, se essa è simmetrica tale è anche l'inversa.
Infatti, se A è simmetrica, si ha l'uguaglianza A = A-1, inoltre A-1= (A-1)-1 e siccome le due operazioni sono permutabili, si ha:
A-1= (A-1)-1.
Quindi, l'inversa di A è uguale alla sua trasposta e ci si trova nella definizione di matrice simmetrica.
Matrice emisimmetrica
Una matrice A di ordine n si dice emisimmetrica se
aik = -aki,
cioè i termini simmetrici della diagonale principale sono simmetrici.
Esempio
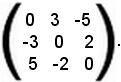
Da tale definizione si deduce che
A = -A-1.
Esempio
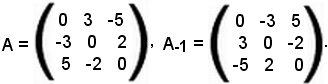
Considerando il determinante di ambo i membri, si ha:
DetA = Det(-A-1) = (-1)nDet(A-1) = (-1)nDetA.
Quindi
DetA = (-1)nDetA.
Una matrice emisimmetrica con n dispari è sempre singolare:
DetA = -DetA,
quindi ha sempre rango diverso da n.
La matrice ha gli elementi della diagonale principale uguali ad uno e quelli della diagonale secondaria uguali a zero, e prende il nome di matrice unità:

Logicamente, essa è sempre di ordine n.
Se A = aik è una matrice del tipo (m, n), ed U è di ordine n, si può considerare la matrice
AU = A,
che è sempre di ordine n. Gli elementi generici sono:
apiδiq = apq.
A tal punto, si asserisce che i termini corrispondenti di due matrici sono uguali.
Si osserva che se m ≠ n, non si può parlare di matrice prodotto AU.
Siano U una matrice unità e B un'altra matrice del tipo (n, m), allora UB è del tipo (n, m) e si dimostra che
UB = B e δpi = biq
e sarà
δqi = 0 se i ≠ q,
δqi = 1 se i = q.
Si osserva che se m ≠ n, non si può parlare di matrice prodotto UB.
Si suppone ora che A sia una matrice quadrata di ordine n ed U la matrice unità:
AU = A, UA = A,
cioè le matrici A ed U sono permutabili.
Siano A e B due matrici dello stesso tipo (h, l) e si consideri la trasposta (AB)-1; si dimostra che
essa è uguale alle trasposte di B-1A-1, cioè:
(AB)-1 = B-1A-1.
Data una matrice quadrata di ordine n, essa è non singolare se il suo rango è diverso da zero. Di tale matrice si può parlare dell'inversa A-1. Se gli elementi di A sono aik, i reciproci sono aki e sono così definiti:
E' stato dimostrato che
apiaiq = δpq,
δpq = 0 se p ≠ q,
δpq = 1 se p ≠ q,
allora si deduce che
AA-1 = U = A-1A.
Si dimostra ora che
(A-1)-1 = A.
Infatti, siccome è noto che
A-1(A-1)-1 = U,
moltiplicando a sinistra per A, risulta
AA-1(A-1)-1 = AU
Data la matrice A non singolare, si considera la sua trasposta, che è anch'essa non singolare. A tal punto, si considera l'inversa della trasposta (A-1)-1 e si dimostra che
(A-1)-1 = (A-1)-1,
cioè la trasposta e l'inversa sono permutabili e si usa il simbolo
A-1-1.
Si dimostra che se A e B sono due matrici quadrate non singolari di ordine n, considerata la matrice prodotto AB, anche questa è non singolare e l'inversa di AB è uguale al prodotto dell'inversa di B per l'inversa di A, cioè:
(AB)-1= B-1A-1.
Infatti, dalla proprietà
AA-1 = U
si deduce che
(AB)-1(AB) = U
Siano T una matrice non singolare di ordine n ed A una matrice quadrata dello stesso ordine.
Si dice trasformata di A mediante T, e si indica con TA, la matrice
TAT-1.
Si dimostra che
DetA = DetTAT-1.
Si dimostra ora che se A e B sono due matrici quadrate di ordine n, considerato il prodotto AB, la trasformata di AB è uguale al prodotto della trasformata di A per la trasformata di B, cioè
T(A B) = TATB.
Infatti, tenendo conto che U = T-1T, si ha:
T(A B) = TAABT-1 = TAAUBT-1 = (TAAT-1)(TBT-1)= TATB.
Siano A una matrice quadrata di ordine n ed U la matrice unità. Si considera ora la matrice
A - ρU,
con ρ indeterminato. Di tale matrice quadrata si considera il determinante, ottenendo così un polinomio nell'indeterminata ρ di grado n, che si chiama polinomio caratteristica di ρ.
Essendo
A = aik, U = δik,
l'elemento generico di A - ρU è
aik - ρδik.
La matrice è dunque
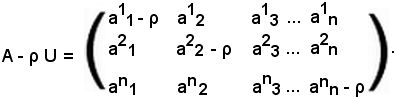
Il determinante
Det(A - ρU) = U
è l'equazione caratteristica.
Siano T una matrice quadrata non singolare ed A un'altra matrice; si consideri inoltre la trasformata di T mediante A,TA = TAT-1. Se al posto della matrice A si considera la matrice A - ρU, si ha:
TA - ρU = T(A - ρU)T-1 = (TA - TρU)T-1 = (TA - ρTU)T-1 = TAT-1- ρTUT-1= TA - ρU.
Considerando
DetTA = Det(TA - ρU) = Det(A - ρU),
si ha che il polinomio della matrice A trasformata mediante T, cioè Det(TA - ρU), è uguale a Det(A - ρU), polinomio caratteristico della matrice A.
Matrice ortogonale
Sia A una matrice quadrata di ordine n, si dice che A è una matrice ortogonale se il prodotto con la sua trasformata è uguale alla matrice unità di ordine n, cioè
A = aik, AA-1 = U.
Matrice simmetrica
Una matrice A = aik si dice simmetrica se
aik = aki,
cioè i termini simmetrici sono uguali.
Una matrice simmetrica è uguale alla sua trasposta.
Dalla proprietà
(A-1)-1= A
nel caso di una matrice non singolare, se essa è simmetrica tale è anche l'inversa.
Infatti, se A è simmetrica, si ha l'uguaglianza A = A-1, inoltre A-1= (A-1)-1 e siccome le due operazioni sono permutabili, si ha:
A-1= (A-1)-1.
Quindi, l'inversa di A è uguale alla sua trasposta e ci si trova nella definizione di matrice simmetrica.
Matrice emisimmetrica
Una matrice A di ordine n si dice emisimmetrica se
aik = -aki,
cioè i termini simmetrici della diagonale principale sono simmetrici.
Esempio

Da tale definizione si deduce che
A = -A-1.
Esempio
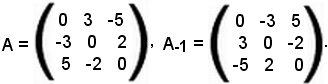
Considerando il determinante di ambo i membri, si ha:
DetA = Det(-A-1) = (-1)nDet(A-1) = (-1)nDetA.
Quindi
DetA = (-1)nDetA.
Una matrice emisimmetrica con n dispari è sempre singolare:
DetA = -DetA,
quindi ha sempre rango diverso da n.