NUMERI REALI ---> INDICE
Sia Q l'insieme
dei numeri interi razionali distribuiti in due classi A e B, secondo il seguente criterio:
1)-ogni razionale appartiene ad una ed una sola classe;
2)-ogni razionale della classe A risulta minore di ciascuno dei razionali della classe B.
Tale distribuzione si chiama sezione dei numeri razionali, o più comunemente numero reale e si indica con (A, B).
Essendo tali distribuzioni infinite, tali sono anche i numeri reali.
Il reale definito da (A, B) si indica con una sola lettera, cioè
α = (A, B).
Esempi di sezioni dei razionali
1)-Sezione dei razionali ottenuta considerando la classe A costituita dal solo elemento zero e la classe B dai rimanenti razionali, cioè
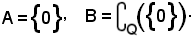
2)-Sezione dei razionali ottenuta considerando le classi A e B costituite dall'insieme dei razionali individuati da m/n, definite come segue:
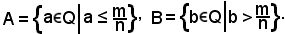
3)-Sezione dei razionali ottenuta considerando le classi A e B costituite dall'insieme dei razionali individuati da m/n, definite come segue:
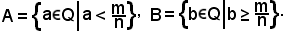
4)-Sezione dei razionali, definita come segue:
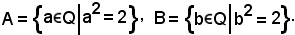
Anche nell'insieme dei reali si definiscono le operazioni di addizione e moltiplicazione.
Addizione
Assegnati due reali
α = (A, B), γ = (C, D),
si costruiscono gl'insiemi
A + C, B + D,
contenenti rispettivamente la somma di un qualsiasi elemento di A con un qualsiasi elemento di C e di un qualsiasi elemento di B con un qualsiasi elemento di D.
Si dimostra facilmente che (A + C, B + D) è una sezione.
Il reale da essa definito si chiama somma di α e γ e si indica con
α + γ.
L'operazione che permette di passare da α a γ,
α + γ = ((A + C), (B + D)),
è l'addizione.
Moltiplicazione
Assegnati due reali
α = (A, B), γ = (C, D),
si costruiscono gl'insiemi
AC, BD,
contenenti rispettivamente il prodotto di un qualsiasi elemento di A con un qualsiasi elemento di C e di un qualsiasi elemento di B con un qualsiasi elemento di D.
Si dimostra facilmente che (AC, BD) è una sezione.
Il reale da essa definito si chiama prodotto di α e γ e si indica con
αγ.
L'operazione che permette di passare da α a γ,
αγ = (AC, BD),
è la moltiplicazione.
Si può dimostrare che l'addizione e la moltiplicazione godono delle proprietà commutativa, associativa e distributiva della somma rispetto al prodotto.
Questo principio, che fa valere le stesse operazioni dei numeri naturali, si chiama principio di permanenza.
Dunque, per i reali valgono le stesse proprietà dei razionali.
Per i reali valgono anche il principio di ampliamento, cioè l'insieme dei razionali è una parte dell'insieme dei reali, ed il criterio del confronto.
Assegnati i reali α e γ, si dice che:
1)-α > γ, se esiste un razionale di A che appartenga a D e non coincida con il suo minimo, cioè con il razionale più piccolo di D.
2)-α < γ, se esiste un razionale di D che appartenga ad A e non coincida con il suo massimo, cioè con il razionale più grande di A.
Si supponga ora che sia stato fissato un criterio di confronto fra segmenti e che siano assegnati il segmento di estremi A e B ed il numero n; in tali condizioni si può parlare di mulltiplo di AB secondo n e si scrive n·AB.
Dati i segmenti AB e BC, si possono presentare due casi:
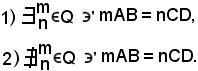
Nel caso 1) i segmenti si dicono commensurabili, mentre nel caso 2) si dicono incommensurabili.
Nel caso 2), si considerano l'insieme Q dei razionali ed i razionali del tipo m/n, per cui risulta
a) nAB < mCD,
b) nB > mCD.
Si pone ora nella classe A la parte di Q costituita dalle frazioni m/n che soddisfano la b) e nella classe B la parte di Q costituita dalle frazioni m/n che soddisfano la a).
In tal modo si è ottenuto una sezione.
Infatti, ogni razionale appartiene ad una sola delle classi.
Occorre dimostrare che ogni elemento della classe A è minore di ciascun elemento della classe B.
Si dimostra prima che la b) non dipende dalla particolare frazione m/n.
Infatti, se
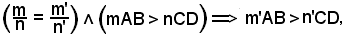
e ciò è vero perchè
mn' = m'n,
dunque, moltiplicando per m' ambo i membri della relazione,
mAB > nCD mm'AB > nm'CD
mm'AB > nm'CD  m'AB > n'CD,
m'AB > n'CD,
come volevasi dimostrare.
Si dimostra ora che, se
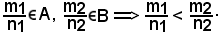
Dire che
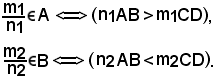
Se AB e CD sono commensurabili, si perviene al numero razionale
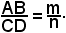
Comunque, in entrambi i casi esiste ed è unico il numero reale α, tale che si abbia AB = αCD, cioè AB multiplo di CD secondo il numero reale α.
Ci si pone ora il problema inverso, cioè assegnato un segmento CD ed un numero reale α, esiste un segmento AB tale che sia multiplo di CD secondo α?
Per la risoluzione di tale problema si considera una semiretta di origine O, un punto U ≠ O ed un numero reale α; si vuol vedere se su questa semiretta esiste un punto A tale che
OA = αOU.
Sia p un intero, p < α, e si consideri un punto P della semiretta, tale che OP = αOU.
Se α è definito da una sezione nei razionali, si indicano con rA i razionali, tali che rA< α, e con RA i punti della semiretta per cui si ha
ORA = rAOU.
Inoltre, si indicano con rB i razionali, tali che rB > α, e con RB i punti del segmento OP, tali che
ORB = rBOU.
Per come sono stati considerati i segmenti, si ha:
ORA < ORB < OP.
Ad esempio, si fissa un ordine secondo cui O precede U ed U precede P, si ha una ripartizione dei punti di OP in due classi.
Si pongono ora nella classe A l'insieme dei punti del segmento OP che precedono almeno un punto del tipo RA, e nella classe B l'insieme dei punti del segmento OP che seguono almeno un punto del tipo RB.
Allora i punti di OP risultano suddivisi in due classi, tali che ogni punto appartiene ad una ed una sola classe, ed ogni punto della prima classe precede ogni punto della seconda classe.
1)-ogni razionale appartiene ad una ed una sola classe;
2)-ogni razionale della classe A risulta minore di ciascuno dei razionali della classe B.
Tale distribuzione si chiama sezione dei numeri razionali, o più comunemente numero reale e si indica con (A, B).
Essendo tali distribuzioni infinite, tali sono anche i numeri reali.
Il reale definito da (A, B) si indica con una sola lettera, cioè
α = (A, B).
Esempi di sezioni dei razionali
1)-Sezione dei razionali ottenuta considerando la classe A costituita dal solo elemento zero e la classe B dai rimanenti razionali, cioè
2)-Sezione dei razionali ottenuta considerando le classi A e B costituite dall'insieme dei razionali individuati da m/n, definite come segue:
3)-Sezione dei razionali ottenuta considerando le classi A e B costituite dall'insieme dei razionali individuati da m/n, definite come segue:
4)-Sezione dei razionali, definita come segue:
Anche nell'insieme dei reali si definiscono le operazioni di addizione e moltiplicazione.
Addizione
Assegnati due reali
α = (A, B), γ = (C, D),
si costruiscono gl'insiemi
A + C, B + D,
contenenti rispettivamente la somma di un qualsiasi elemento di A con un qualsiasi elemento di C e di un qualsiasi elemento di B con un qualsiasi elemento di D.
Si dimostra facilmente che (A + C, B + D) è una sezione.
Il reale da essa definito si chiama somma di α e γ e si indica con
α + γ.
L'operazione che permette di passare da α a γ,
α + γ = ((A + C), (B + D)),
è l'addizione.
Moltiplicazione
Assegnati due reali
α = (A, B), γ = (C, D),
si costruiscono gl'insiemi
AC, BD,
contenenti rispettivamente il prodotto di un qualsiasi elemento di A con un qualsiasi elemento di C e di un qualsiasi elemento di B con un qualsiasi elemento di D.
Si dimostra facilmente che (AC, BD) è una sezione.
Il reale da essa definito si chiama prodotto di α e γ e si indica con
αγ.
L'operazione che permette di passare da α a γ,
αγ = (AC, BD),
è la moltiplicazione.
Si può dimostrare che l'addizione e la moltiplicazione godono delle proprietà commutativa, associativa e distributiva della somma rispetto al prodotto.
Questo principio, che fa valere le stesse operazioni dei numeri naturali, si chiama principio di permanenza.
Dunque, per i reali valgono le stesse proprietà dei razionali.
Per i reali valgono anche il principio di ampliamento, cioè l'insieme dei razionali è una parte dell'insieme dei reali, ed il criterio del confronto.
Assegnati i reali α e γ, si dice che:
1)-α > γ, se esiste un razionale di A che appartenga a D e non coincida con il suo minimo, cioè con il razionale più piccolo di D.
2)-α < γ, se esiste un razionale di D che appartenga ad A e non coincida con il suo massimo, cioè con il razionale più grande di A.
Si supponga ora che sia stato fissato un criterio di confronto fra segmenti e che siano assegnati il segmento di estremi A e B ed il numero n; in tali condizioni si può parlare di mulltiplo di AB secondo n e si scrive n·AB.
Dati i segmenti AB e BC, si possono presentare due casi:
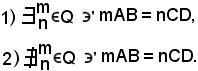
Nel caso 1) i segmenti si dicono commensurabili, mentre nel caso 2) si dicono incommensurabili.
Nel caso 2), si considerano l'insieme Q dei razionali ed i razionali del tipo m/n, per cui risulta
a) nAB < mCD,
b) nB > mCD.
Si pone ora nella classe A la parte di Q costituita dalle frazioni m/n che soddisfano la b) e nella classe B la parte di Q costituita dalle frazioni m/n che soddisfano la a).
In tal modo si è ottenuto una sezione.
Infatti, ogni razionale appartiene ad una sola delle classi.
Occorre dimostrare che ogni elemento della classe A è minore di ciascun elemento della classe B.
Si dimostra prima che la b) non dipende dalla particolare frazione m/n.
Infatti, se
e ciò è vero perchè
mn' = m'n,
dunque, moltiplicando per m' ambo i membri della relazione,
mAB > nCD
come volevasi dimostrare.
Si dimostra ora che, se
Dire che
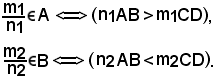
Siccome n1 ≠ 0, n2 ≠ 0, si può moltiplicare la prima disuguaglianza per n2 e la seconda per n1, quindi da
n1AB > m1CD n2AB < m2CD
n2AB < m2CD  n1n2AB > m1n2CD
n1n2AB > m1n2CD  n1n2AB < n1m2CD
n1n2AB < n1m2CD 
 m1n2CD < n1n2AB < n1m2CD
m1n2CD < n1n2AB < n1m2CD  m1n2CD < n1m2CD
m1n2CD < n1m2CD  m1n2 < n1m2,
m1n2 < n1m2,
e da ciò si ha:
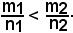
La sezione così ottenuta individua il numero
α = (A, B).
Infine, se AB e CD sono incommensurabili, si perviene al numero reale α, che non è razionale bensì irrazionale.
In tal caso:
AB = αCD,
oppure
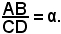
n1AB > m1CD
e da ciò si ha:
La sezione così ottenuta individua il numero
α = (A, B).
Infine, se AB e CD sono incommensurabili, si perviene al numero reale α, che non è razionale bensì irrazionale.
In tal caso:
AB = αCD,
oppure
Se AB e CD sono commensurabili, si perviene al numero razionale
Comunque, in entrambi i casi esiste ed è unico il numero reale α, tale che si abbia AB = αCD, cioè AB multiplo di CD secondo il numero reale α.
Ci si pone ora il problema inverso, cioè assegnato un segmento CD ed un numero reale α, esiste un segmento AB tale che sia multiplo di CD secondo α?
Per la risoluzione di tale problema si considera una semiretta di origine O, un punto U ≠ O ed un numero reale α; si vuol vedere se su questa semiretta esiste un punto A tale che
OA = αOU.
Sia p un intero, p < α, e si consideri un punto P della semiretta, tale che OP = αOU.
Se α è definito da una sezione nei razionali, si indicano con rA i razionali, tali che rA< α, e con RA i punti della semiretta per cui si ha
ORA = rAOU.
Inoltre, si indicano con rB i razionali, tali che rB > α, e con RB i punti del segmento OP, tali che
ORB = rBOU.
Per come sono stati considerati i segmenti, si ha:
ORA < ORB < OP.
Ad esempio, si fissa un ordine secondo cui O precede U ed U precede P, si ha una ripartizione dei punti di OP in due classi.
Si pongono ora nella classe A l'insieme dei punti del segmento OP che precedono almeno un punto del tipo RA, e nella classe B l'insieme dei punti del segmento OP che seguono almeno un punto del tipo RB.
Allora i punti di OP risultano suddivisi in due classi, tali che ogni punto appartiene ad una ed una sola classe, ed ogni punto della prima classe precede ogni punto della seconda classe.
In
tali condizioni esiste uno ed un solo punto della prima e della
seconda classe tale che precede ciascun punto della seconda e segue ciascun della prima
classe. Tale punto, indicato con Q, è tale che
OQ = αOU.
In tal modo si è ottenuta una bigezione tra i punti della semiretta ed i numeri reali.
OQ = αOU.
In tal modo si è ottenuta una bigezione tra i punti della semiretta ed i numeri reali.