NUMERI RELATIVI ---> INDICE
Si consideri l'insieme delle coppie ordinate dei numeri reali, elementi del prodotto R 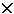 R = R2; due coppie ordinate (α, β), (γ, δ) sono in relazione
R = R2; due coppie ordinate (α, β), (γ, δ) sono in relazione 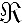 se e solo se α + δ = β + γ, cioè
se e solo se α + δ = β + γ, cioè
(α, β)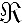 (γ, δ)
(γ, δ)  α + δ = β + γ.
α + δ = β + γ.
Si dimostra che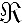 è una relazione di equivalenza, cioè
è una relazione di equivalenza, cioè
1)-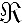 è riflessiva: (α, β)
è riflessiva: (α, β)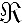 (α, β).
(α, β).
Infatti:
(α, β)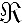 (α, β)
(α, β)  α + β = β + α,
α + β = β + α,
e ciò è vero per la proprietà commutativa dei reali.
2)-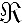 è simmetrica: (α, β)
è simmetrica: (α, β)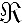 (γ, δ)
(γ, δ)  (γ, δ)
(γ, δ)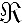 (α, β).
(α, β).
Infatti:
(α, β)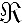 (γ, δ)
(γ, δ)  α + δ = β + γ,
α + δ = β + γ,
per la proprietà commutativa dei reali
γ + β = δ + α (γ, δ)
(γ, δ)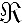 (α, β).
(α, β).
3)-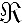 è transitiva, cioè (α, β)
è transitiva, cioè (α, β)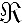 (γ, δ), (γ, δ)
(γ, δ), (γ, δ)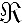 (ε, φ)
(ε, φ)  (α, β)
(α, β)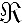 (ε, φ).
(ε, φ).
Infatti:
(α, β)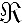 (γ, δ), (γ, δ)
(γ, δ), (γ, δ)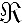 (ε, φ)
(ε, φ)  α + δ = β + γ, γ + φ = δ + ε,
α + δ = β + γ, γ + φ = δ + ε,
aggiungendo α ad ambo i membri della seconda uguaglianza, si ha
α + δ = β + γ, α + γ + φ = α + δ + ε α + γ + φ = β + γ + ε
α + γ + φ = β + γ + ε  α + φ = β + ε = ε + β
α + φ = β + ε = ε + β 
 (α, β)
(α, β)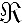 (ε, φ).
(ε, φ).
Si consideri l'insieme quoziente
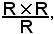
ad esso si dà il nome di insieme dei numeri relativi.Anche per i numeri relativi si ha un criterio di confronto.
Si dice che due coppie ordinate di reali individuano lo stesso relativo, se e solo se risulta
α + δ = β + γ,
(α, β) = (γ, δ) α + δ = β + γ.
α + δ = β + γ.
Si dice che il numero relativo individuato dalla coppia (α, β) è maggiore o minore di quello individuato dalla coppia (γ, δ), se e solo se α + δ è maggiore o minore di β + γ, cioè
(α, β) > (γ, δ) α + δ > β + γ,
α + δ > β + γ,
(α, β) < (γ, δ) α + δ < β + γ.
α + δ < β + γ.
Anche nell'insieme dei relativi si definiscono l'addizione e la moltiplicazione.
Addizione
Si considerino inoltre due relativi (α', β'), (γ', δ'), che individuano gli stessi relativi di (α, β), (γ, δ), si dimostra che la loro somma (α' + γ', β' + δ') è uguale alla precedente (α + γ, β + δ), cioè:
(α' + γ', β' + δ') = (α + γ, β + δ).
Si può quindi dire che l'addizione è una legge di composizione interna.
Infatti, affinchè
(α, β) = (α', β'), (γ, δ) = (γ', δ'),
occorre che
α + β' = α' + β, γ + δ' = γ' + δ.
Sommando membro a membro, si ha:
α + β' + γ + δ' = α' + β + γ' + δ,
(α + γ) + (β' + δ') = (β + δ) + (α' + γ'),
e questa è la condizione che sia
(α' + γ', β' + δ') = (α + γ, β + δ),
come volevasi dimostrare.
Moltiplicazione
Si considerino inoltre due relativi (α', β'), (γ', δ'), che individuano gli stessi relativi di (α, β), (γ, δ), si dimostra che il loro prodotto (α'β')(γ'δ') è uguale al precedente (αβ)(γδ), cioè
(α'β')(γ'δ') = (αβ)(γδ).
Si può quindi dire che la moltiplicazione è una legge di composizione interna.
Infatti, affinchè
(α, β) = (α', β'), (γ, δ) = (γ' δ'),
occorre che
α + β' = α' + β, γ + δ' = γ' + δ.
Moltiplicando membro a membro, si ha:
(α + β')(γ + δ') = (α' + β)(γ' + δ),
e questa è la condizione che sia
(αβ)(γδ) = (α'β')(γ'δ'),
come volevasi dimostrare.
Si dimostra che per la somma ed il prodotto valgono le proprietà commutativa, associativa e distributiva della somma rispetto al prodotto.
Questo principio, che fa valere le stesse operazioni dei numeri reali, si chiama principio di permanenza.
Dunque, per i relativi valgono le stesse proprietà dei reali.
Per i relativi vale anche il principio di ampliamento, cioè l'insieme dei reali è una parte dell'insieme dei relativi.
Infatti, si può considerare quella parte dei relativi i cui elementi sono individuati dalle coppie ordinate del tipo (a, 0): tale parte è identificabile con l'insieme dei reali; al numero relativo individuato dalla coppia (a, 0) si associa cioè il reale a. Viceversa, considerato il reale a, il numero relativo da cui esso proviene è dato dalla coppia ordinata (a, 0).
La somma dei relativi individuati da (a, 0) fornisce numeri relativi dello stesso tipo, cioè:
(a, 0)(b, 0) = (ab, 0).
Dunque, la prima coordinata della coppia ordinata somma è proprio quella derivante dalla coppia ordinata (a + b, 0).
Allo stesso modo si ragiona per il prodotto:
il prodotto dei relativi individuati da (a, 0) fornisce numeri relativi dello stesso tipo, cioè:
(a, 0)(b, 0) = (ab, 0).
Dunque, la prima coordinata della coppia ordinata prodotto è proprio quella derivante dalla coppia ordinata (ab, 0).
Infatti, se
(a, 0) = (b, 0) a = b,
a = b,
(a, 0) > (b, 0) a + 0 > b + 0
a + 0 > b + 0  a > b,
a > b,
(a, 0) < (b, 0) a + 0 < b + 0
a + 0 < b + 0  a < b.
a < b.
(α, β)
Si dimostra che
1)-
Infatti:
(α, β)
e ciò è vero per la proprietà commutativa dei reali.
2)-
Infatti:
(α, β)
per la proprietà commutativa dei reali
γ + β = δ + α
3)-
Infatti:
(α, β)
aggiungendo α ad ambo i membri della seconda uguaglianza, si ha
α + δ = β + γ, α + γ + φ = α + δ + ε
Si consideri l'insieme quoziente
ad esso si dà il nome di insieme dei numeri relativi.Anche per i numeri relativi si ha un criterio di confronto.
Si dice che due coppie ordinate di reali individuano lo stesso relativo, se e solo se risulta
α + δ = β + γ,
cioè
(α, β) = (γ, δ)
Si dice che il numero relativo individuato dalla coppia (α, β) è maggiore o minore di quello individuato dalla coppia (γ, δ), se e solo se α + δ è maggiore o minore di β + γ, cioè
(α, β) > (γ, δ)
(α, β) < (γ, δ)
Anche nell'insieme dei relativi si definiscono l'addizione e la moltiplicazione.
Addizione
Si considerino due relativi individuati dalle coppie (α, β), (γ, δ), per loro somma s'intende il relativo individuato da (α + γ, β + δ), cioè
(α, β) + (γ, δ) = (α + γ, β + δ).
(α, β) + (γ, δ) = (α + γ, β + δ).
Si considerino inoltre due relativi (α', β'), (γ', δ'), che individuano gli stessi relativi di (α, β), (γ, δ), si dimostra che la loro somma (α' + γ', β' + δ') è uguale alla precedente (α + γ, β + δ), cioè:
(α' + γ', β' + δ') = (α + γ, β + δ).
Si può quindi dire che l'addizione è una legge di composizione interna.
Infatti, affinchè
(α, β) = (α', β'), (γ, δ) = (γ', δ'),
occorre che
α + β' = α' + β, γ + δ' = γ' + δ.
Sommando membro a membro, si ha:
α + β' + γ + δ' = α' + β + γ' + δ,
(α + γ) + (β' + δ') = (β + δ) + (α' + γ'),
e questa è la condizione che sia
(α' + γ', β' + δ') = (α + γ, β + δ),
come volevasi dimostrare.
Moltiplicazione
Si considerino due relativi individuati dalle coppie (α, β), (γ, δ), per loro prodotto s'intende il relativo individuato dalla coppia (αγ + βδ, αδ + βγ), cioè
(α, β)(γ, δ) = (αγ + βδ, αδ + βγ).
(α, β)(γ, δ) = (αγ + βδ, αδ + βγ).
Si considerino inoltre due relativi (α', β'), (γ', δ'), che individuano gli stessi relativi di (α, β), (γ, δ), si dimostra che il loro prodotto (α'β')(γ'δ') è uguale al precedente (αβ)(γδ), cioè
(α'β')(γ'δ') = (αβ)(γδ).
Si può quindi dire che la moltiplicazione è una legge di composizione interna.
Infatti, affinchè
(α, β) = (α', β'), (γ, δ) = (γ' δ'),
occorre che
α + β' = α' + β, γ + δ' = γ' + δ.
Moltiplicando membro a membro, si ha:
(α + β')(γ + δ') = (α' + β)(γ' + δ),
e questa è la condizione che sia
(αβ)(γδ) = (α'β')(γ'δ'),
come volevasi dimostrare.
Si dimostra che per la somma ed il prodotto valgono le proprietà commutativa, associativa e distributiva della somma rispetto al prodotto.
Questo principio, che fa valere le stesse operazioni dei numeri reali, si chiama principio di permanenza.
Dunque, per i relativi valgono le stesse proprietà dei reali.
Per i relativi vale anche il principio di ampliamento, cioè l'insieme dei reali è una parte dell'insieme dei relativi.
Infatti, si può considerare quella parte dei relativi i cui elementi sono individuati dalle coppie ordinate del tipo (a, 0): tale parte è identificabile con l'insieme dei reali; al numero relativo individuato dalla coppia (a, 0) si associa cioè il reale a. Viceversa, considerato il reale a, il numero relativo da cui esso proviene è dato dalla coppia ordinata (a, 0).
La somma dei relativi individuati da (a, 0) fornisce numeri relativi dello stesso tipo, cioè:
(a, 0)(b, 0) = (ab, 0).
Dunque, la prima coordinata della coppia ordinata somma è proprio quella derivante dalla coppia ordinata (a + b, 0).
Allo stesso modo si ragiona per il prodotto:
il prodotto dei relativi individuati da (a, 0) fornisce numeri relativi dello stesso tipo, cioè:
(a, 0)(b, 0) = (ab, 0).
Dunque, la prima coordinata della coppia ordinata prodotto è proprio quella derivante dalla coppia ordinata (ab, 0).
Infatti, se
(a, 0) = (b, 0)
(a, 0) > (b, 0)
(a, 0) < (b, 0)