PROPRIETA' NELL'INSIEME DELLE TRASFORMAZIONI AFFINI ---> INDICE
Si indichi con 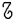 l'insieme delle trasformazioni affini in sé:
l'insieme delle trasformazioni affini in sé:
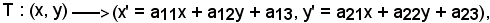
in cui
aij R
R
con
i = 1, 2 e j = 1, 2, 3
e
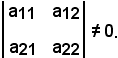
Si dimostra ora la seguente equivalenza:
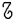 gruppo di trasformazioni di R2
gruppo di trasformazioni di R2  a)
a)  T
T
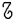 ,
,  T'
T'
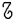 : T'T
: T'T
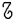 , b)
, b)  T
T
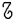 : T-1
: T-1
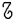 ,
,
cioè il prodotto di due trasformazioni T e T' è anch'esso una trasformazione appartenente all'insieme delle trasformazioni affini di R2, inoltre per ogni trasformazione dell'insieme di trasformazioni affini di R2, anche la sua inversa appartiene al gruppo delle trasformazioni di R2.
Dimostrazione a).
Si considera una trasformazione T definita come sopra, inoltre sia ora
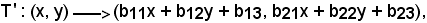
in cui
bij R
R
tale che
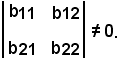
Si consideri ora il seguente prodotto:
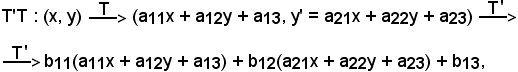
quindi
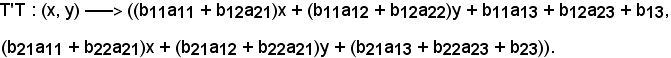
Ponendo
c11 = b11a11 + b12a21,
c12 = b11a12 + b12a22,
c13 = b11a13 + b12a23 + b13,
c21 = b21a11 + b22a21,
c22 = b21a12 + b22a21,
c23 = b21a13 + b22a23 + b23,
si ha:
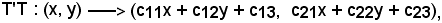
con
c11 R, c13
R, c13 R, c23
R, c23 R.
R.
Affinché T'T sia una trasformazione affine, dev'essere
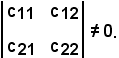
Infatti
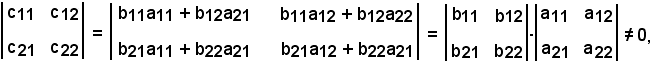
perchè per ipotesi i due determinanti del prodotto sono entrambi diversi da zero, come volevasi dimostrare.
Dimostrazione b).
Si considera
T
 ,
,
si deve dimostrare che
T-1
 .
.
Sia
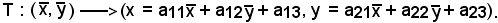
Siccome T è bigettiva,
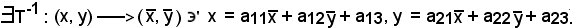
Per trovare i valori di

basta risolvere il sistema formato dalle seguenti due equazioni, che ammette una sola soluzione, pertanto il suo determinante a è diverso da zero, cioè:

Se il determinante è diverso da zero, quella in questione è una trasformazione affine:
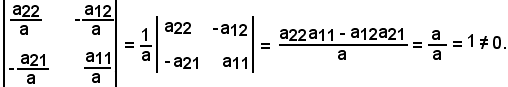
Teorema di esistenza ed unicità per trasformazioni affini di R2.Se
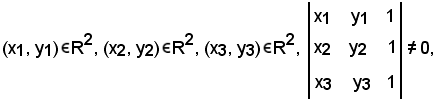
e se
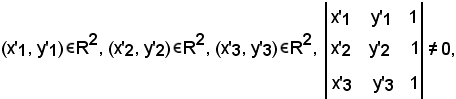
 T
T

 i = 1, 2, 3 : T(xi, yi) = (x'i, y'i).
i = 1, 2, 3 : T(xi, yi) = (x'i, y'i).
Dimostrazione
Per dimostrare che esiste una trasformazione affine di R2 in sé, la T è definita da
x' = a11x + a12y + a13, y' = a21x + a22y + a23,
 T
T

 i = [1, 3] : T(xi, yi) = (x'i, y'i)
i = [1, 3] : T(xi, yi) = (x'i, y'i) 
 aij
aij R, i = 1, 2
R, i = 1, 2  j = 1, 2, 3
j = 1, 2, 3 
 x'i = a11xi + a12yi + a13, y'i = a21xi + a22yi + a23.
x'i = a11xi + a12yi + a13, y'i = a21xi + a22yi + a23.
Considerando x'1, x'2, x'3, y'1, y'2, y'3, ed applicando le condizioni suddette, si ottengono due sistemi lineari di tre equazioni in tre incognite, rispettivamente a11, a12, a13 ed a21, a22, a23, che ammettono complessivamente sei soluzioni, cioè:
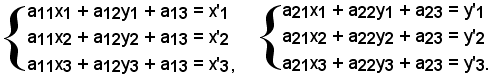
Siccome per ipotesi

i sistemi ammettono una sola soluzione, quindi risolvendo, si ha:
x'i = a11xi + a12yi + a13, y'i = a21xi + a22yi + a23.
Per dimostrare che queste sono le equazioni di una trasformazione di R2, basta provare che il determinante del nuovo sistema è diverso da zero.
Considerando il secondo determinante diverso da zero, e sottraendo dalla prima riga la terza, e dalla seconda riga la terza, si ha:
a11(x1 - x3) + a12(y1 - y3) = x'1 - x'3,
a11(x2 - x3) + a12(y2 - y3) = x'2 - x'3.
Con analogo ragionamento per l'altro sistema, si ha:
a21(x1 - x3) + a22(y1 - y3) = y'1 - y'3,
a21(x2 - x3) + a22(y2 - y3) = y'2 - y'3.
Essendo il secondo determinante diverso da zero ed anche uguale a quello ottenuto sottraendo dalla prima riga la terza, e dalla seconda riga la terza, si ha:
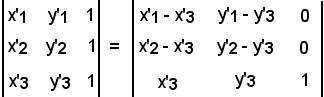
e, sviluppando secondo gli elementi della seconda colonna, risulta
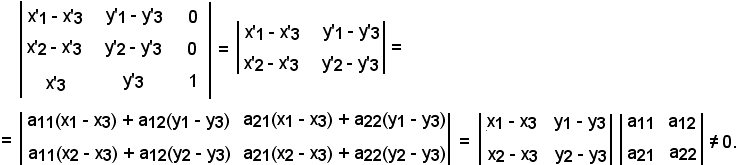
E' quindi dimostrato che
 T
T

 i = 1, 2, 3 : T(xi, yi) = (x'i, y'i).
i = 1, 2, 3 : T(xi, yi) = (x'i, y'i).
Affinità sul piano
Si consideri il piano π, si richiama la seguente definizione:

In tale definizione f-1Tf ha senso, in quanto il seguente diagramma è commutativo:
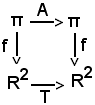
Per tale motivo si ha:
fA = Tf f-1fA = f-1Tf
f-1fA = f-1Tf  A = f-1Tf.
A = f-1Tf.
L'insieme delle trasformazioni affini è un gruppo.
delle trasformazioni affini è un gruppo.
Quindi, si deve dimostrare:
1) A
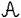 , A'
, A'
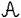
 A'A
A'A
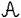 ,
,
2) A
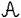
 A-1
A-1
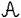 .
.
Dimostrazione 1).
A
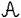 , A'
, A'
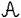

 T
T
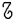
 A = f-1Tf,
A = f-1Tf,  T'
T'
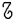
 A' = f-1T'f
A' = f-1T'f  A'A = (f-1T'f)(f-1Tf) = f-1(T'T)f
A'A = (f-1T'f)(f-1Tf) = f-1(T'T)f 
 T'T
T'T
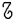
 A'A = f-1(T'T)f
A'A = f-1(T'T)f  A'A
A'A
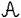 .
.
Dimostrazione 2).
A
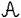

 T
T
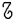
 A = f-1Tf
A = f-1Tf  A-1 = (f-1T'f)-1 = fT-1f-1
A-1 = (f-1T'f)-1 = fT-1f-1  T-1
T-1
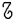
 A-1 = f-1T-1f
A-1 = f-1T-1f 
 A-1
A-1
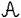 .
.
Teorema di esistenza ed unicità delle affinità
Se P1, P2, P3 sono tre punti non allineati del piano π, e se inoltre P'1, P'2, P'3 sono altri tre punti non allineati del piano π, allora
 A
A
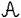
 A(Pi) = P'i (i = 1, 2, 3).
A(Pi) = P'i (i = 1, 2, 3).
Sia, nel riferimento (O, Ux, Uy),
(O, Ux, Uy),
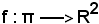
e si supponga che
f(Pi) = (xi, yi), f(P'i) = (x'i, y'i).
Si osserva ora che:

Quindi, ci si trova di fronte a tre coppie di numeri
(x1, y1), (x2, y2), (x3, y3),
ed analogamente
(x'1, y'1), (x'2, y'2), (x'3, y'3),
che soddisfano le condizioni viste, allora
 T
T
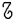
 T(xi, yi) = (x'i, y'i), i = 1, 2, 3.
T(xi, yi) = (x'i, y'i), i = 1, 2, 3.
Si considera ora l'affinità A = f-1Tf, e si dimostra che
A(Pi) = P'i , i = 1, 2, 3.
i = 1, 2, 3.
Infatti:
A(Pi) = f-1(T(f(Pi))) = f-1(T(xi, yi)) = f-1(x'i, y'i) = P'i, i = 1, 2, 3.
i = 1, 2, 3.
Precisamente, questa affinità trasforma punti della prima terna in punti della seconda. Per dimostrare che l'affinità A é unica, se ne considera un'altra e si verifica che esse coincidano.
Sia essa
A'
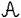
 A'(Pi) = P'i
A'(Pi) = P'i 
 T'
T'
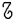
 T' = fA'f-1
T' = fA'f-1  T'(xi, yi) = f(A'(f-1(xi, yi))) = f(A'(Pi)) = f(P'i) =
T'(xi, yi) = f(A'(f-1(xi, yi))) = f(A'(Pi)) = f(P'i) =
= (x'i, y'i) T = T'
T = T'  A' = A.
A' = A.
Ogni affinità trasforma rette in rette, oppure l'immagine mediante un'affinità di una retta è anche una retta:
 A
A
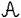 ,
,  r = retta: A(r) = r' retta.
r = retta: A(r) = r' retta.
Sia r una retta e si considerino
P1 ≠ P2 r = [P1, P2].
r = [P1, P2].
Si osserva ora che:
A(r) retta
 P
P r = [P1, P2]: A(P)
r = [P1, P2]: A(P) r' = [P'1, P'2],
r' = [P'1, P'2],
tenendo conto che
P'1 = A(P1), P'2 = A(P'2),
ed applicando la definizione di affinità e considerando l'equazione parametrica, fissato un sistema di riferimento (O, Ux, Uy), ed il suo sistema coordinato, si ha:
(O, Ux, Uy), ed il suo sistema coordinato, si ha:
f(P1) = (x1, y1), f(P2) = (x2, y2), f(P) = (x, y) A = f-1Tf,
A = f-1Tf,
T) x' = a11x + a12y + a13, y' = a21x + a22y + a23.
Si procurano ora le coordinate dei punti trasformati mediante l'affinità in P1 e P2.
Essendo
P'1 = A(P1), f(P'1) = f(A(P1)) = T(f(P1)) = T(x1, y1) = (x'1, y'1),
x'1 = a11x1 + a12y1 + a13, y'1 = a21x1 + a22y1 + a23,
quindi
f(P) = (x'2, y'2), x'2 = a11x2 + a12y2 + a13, y'1 = a21x2 + a22y2 + a23,
infine, se
P r = [P1, P2]
r = [P1, P2] 
 t
t R
R  f(P) = (x, y), x = x1 + (x2 - x1)t, y = y1 + (y2 - y1)t.
f(P) = (x, y), x = x1 + (x2 - x1)t, y = y1 + (y2 - y1)t.
Ora
f(A(P)) = T(x, y) = (x', y'),
x' = a11(x1 + (x2 - x1)t) + a12(y1 + (y2 - y1)t) + a13,
y' = a21(x1 + (x2 - x1)t) + a22(y1 + (y2 - y1)t) + a23,
da ciò segue
x' = x'1 + (x'2 - x'1)t, y' = y'1 + (y'2 - y'1)t,
allora
(A(P)) r' = [P'1, P'2].
r' = [P'1, P'2].
Ogni affinità conserva i rapporti semplici.
A
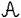 , P
, P π, P1
π, P1 π, P2
π, P2 π
π  P2 ≠ P1
P2 ≠ P1  (PP2P1) = (PP'2P'1).
(PP2P1) = (PP'2P'1).
Si consideri il rapporto semplice (PP2P1) nei seguenti casi.
1) r = [P2, P1] non parallela all'asse y:
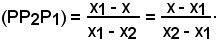
2) r = [P2, P1] non parallela all'asse x:
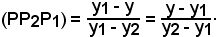
Siccome P è allineato con P2 e P1,
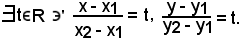
Quindi, in ogni caso, si può scrivere
(PP2P1) = t.
Si consideri ora il rapporto semplice (PP'2P'1) negli stessi casi precedenti.
1)' r' = [P'2, P'1] non parallela all'asse y:
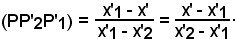
2) r = [P'2, P'1] non parallela all'asse x:
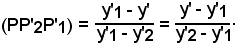
Siccome P è allineato con P2 e P1,
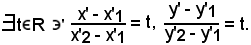
Quindi, in ogni caso, si può scrivere
(PP'2P'1) = t.
In definitiva, come volevasi, si ha:
(PP2P1) = (PP'2P'1).
Equazione della retta trasformata
Siano
r) ax + by + c = 0, r') a'x + b'y + c' = 0,
siccome l'immagine di r è una retta, si ha un'equazione non nota.
Si devono cioè trovare le relazioni tra a ed a', b e b', c e c' mediante A = f-1Tf.
Supponendo che
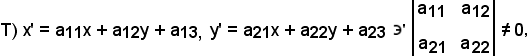
dire che r) è equazione della retta, vuol dire che
(x, y) R2
R2  ax + by + c = 0
ax + by + c = 0  f-1(x, y) = P
f-1(x, y) = P R.
R.
Siccome r' è trasformazione di r, segue
P' = A(P) r
r  f(P') = (x', y'),
f(P') = (x', y'),
che sono note poichè si conosce A, e devono formare una soluzione di
a'x' + b'y' + c' = 0 (x, y)
(x, y)  a'(a11x + a12y + a13) + b'(a21x + a22y + a23) + c' = 0
a'(a11x + a12y + a13) + b'(a21x + a22y + a23) + c' = 0 
 (x, y)
(x, y)  a'a11x + a'a12y + a'a13+ b'a21x + b'a22y + b'a23 + c' = 0
a'a11x + a'a12y + a'a13+ b'a21x + b'a22y + b'a23 + c' = 0 
 (x, y)
(x, y)  (a'a11 + b'a21)x + (a'a12 + b'a22)y + a'a13 + b'a23 + c' = 0 (*).
(a'a11 + b'a21)x + (a'a12 + b'a22)y + a'a13 + b'a23 + c' = 0 (*).
Si è quindi trovato che (x, y) non solo è soluzione di ax + by + c = 0, ma anche di (*), quindi le due equazioni di primo grado sono equivalenti e pertanto
 ρ≠0
ρ≠0  ρa = a'a11 + b'a21, ρb = a'a12 + b'a22, ρc = a'a13 + b'a23 + c',
ρa = a'a11 + b'a21, ρb = a'a12 + b'a22, ρc = a'a13 + b'a23 + c',
quindi, noti a, b, c, si possono determinare a', b', c', dando a ρ un valore arbitrario diverso da zero. Fissando ρ = 1, nelle prime due equazioni le incognite sono a' e b', e siccome c'è una combinazione lineare, si può calcolare l'unica soluzione di a' e b' che sostituite nella terza uguaglianza permettono di ricavare c'. Quindi, queste relazioni permettono di trovare l'equazione della retta trasformata.
Ogni affinità trasforma rette parallele in rette parallele
Si può anche dire che ogni affinità trasforma direzioni in direzioni.Si considerino
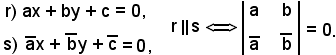
Si considerino ora le trasformate di r e di s indicate con
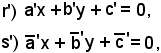
in modo che valgano ancora le relazioni precedenti.
Sotto tali ipotesi si vuole dimostrare che r'||s'.
Si considera il determinante suddetto, si moltiplica la prima riga per ρ e la seconda per σ, infine si sostituiscono i valori di ρa, ρb,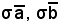 , ottenendo quanto segue:
, ottenendo quanto segue:

Pertanto risulta il prodotto di due determinanti uguale a zero e, poichè il secondo è diverso da zero, necessariamente è
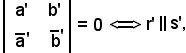
come volevasi dimostrare.
in cui
aij
con
i = 1, 2 e j = 1, 2, 3
e

Si dimostra ora la seguente equivalenza:
cioè il prodotto di due trasformazioni T e T' è anch'esso una trasformazione appartenente all'insieme delle trasformazioni affini di R2, inoltre per ogni trasformazione dell'insieme di trasformazioni affini di R2, anche la sua inversa appartiene al gruppo delle trasformazioni di R2.
Dimostrazione a).
Si considera una trasformazione T definita come sopra, inoltre sia ora
in cui
bij
tale che
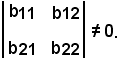
Si consideri ora il seguente prodotto:
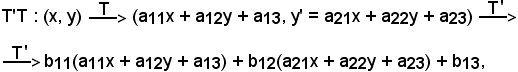
quindi
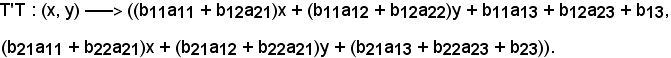
c11 = b11a11 + b12a21,
c12 = b11a12 + b12a22,
c13 = b11a13 + b12a23 + b13,
c21 = b21a11 + b22a21,
c22 = b21a12 + b22a21,
c23 = b21a13 + b22a23 + b23,
si ha:
con
c11
Affinché T'T sia una trasformazione affine, dev'essere

Infatti
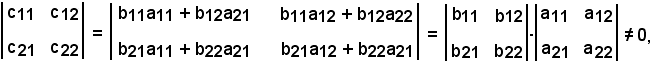
perchè per ipotesi i due determinanti del prodotto sono entrambi diversi da zero, come volevasi dimostrare.
Dimostrazione b).
Si considera
T
si deve dimostrare che
T-1
Sia
Siccome T è bigettiva,
Per trovare i valori di
basta risolvere il sistema formato dalle seguenti due equazioni, che ammette una sola soluzione, pertanto il suo determinante a è diverso da zero, cioè:

Se il determinante è diverso da zero, quella in questione è una trasformazione affine:
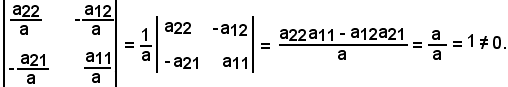
Teorema di esistenza ed unicità per trasformazioni affini di R2.
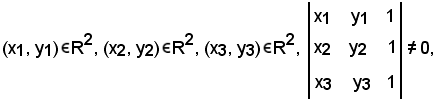
e se
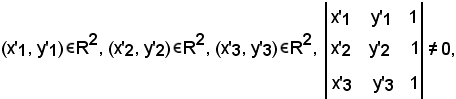
Dimostrazione
Per dimostrare che esiste una trasformazione affine di R2 in sé, la T è definita da
x' = a11x + a12y + a13, y' = a21x + a22y + a23,
Considerando x'1, x'2, x'3, y'1, y'2, y'3, ed applicando le condizioni suddette, si ottengono due sistemi lineari di tre equazioni in tre incognite, rispettivamente a11, a12, a13 ed a21, a22, a23, che ammettono complessivamente sei soluzioni, cioè:
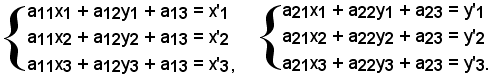
Siccome per ipotesi

i sistemi ammettono una sola soluzione, quindi risolvendo, si ha:
x'i = a11xi + a12yi + a13, y'i = a21xi + a22yi + a23.
Per dimostrare che queste sono le equazioni di una trasformazione di R2, basta provare che il determinante del nuovo sistema è diverso da zero.
Considerando il secondo determinante diverso da zero, e sottraendo dalla prima riga la terza, e dalla seconda riga la terza, si ha:
a11(x1 - x3) + a12(y1 - y3) = x'1 - x'3,
a11(x2 - x3) + a12(y2 - y3) = x'2 - x'3.
Con analogo ragionamento per l'altro sistema, si ha:
a21(x1 - x3) + a22(y1 - y3) = y'1 - y'3,
a21(x2 - x3) + a22(y2 - y3) = y'2 - y'3.
Essendo il secondo determinante diverso da zero ed anche uguale a quello ottenuto sottraendo dalla prima riga la terza, e dalla seconda riga la terza, si ha:
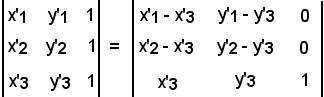
e, sviluppando secondo gli elementi della seconda colonna, risulta
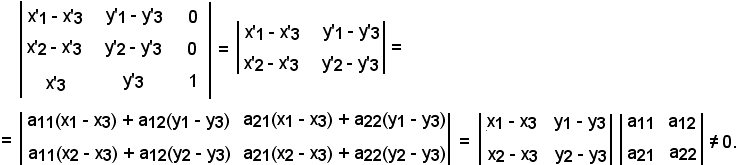
E' quindi dimostrato che
Affinità sul piano
Si consideri il piano π, si richiama la seguente definizione:
In tale definizione f-1Tf ha senso, in quanto il seguente diagramma è commutativo:

Per tale motivo si ha:
fA = Tf
L'insieme
Quindi, si deve dimostrare:
1) A
2) A
Dimostrazione 1).
A
Dimostrazione 2).
A
Teorema di esistenza ed unicità delle affinità
Se P1, P2, P3 sono tre punti non allineati del piano π, e se inoltre P'1, P'2, P'3 sono altri tre punti non allineati del piano π, allora
Sia, nel riferimento
e si supponga che
f(Pi) = (xi, yi), f(P'i) = (x'i, y'i).
Si osserva ora che:

Quindi, ci si trova di fronte a tre coppie di numeri
(x1, y1), (x2, y2), (x3, y3),
ed analogamente
(x'1, y'1), (x'2, y'2), (x'3, y'3),
che soddisfano le condizioni viste, allora
Si considera ora l'affinità A = f-1Tf, e si dimostra che
A(Pi) = P'i ,
Infatti:
A(Pi) = f-1(T(f(Pi))) = f-1(T(xi, yi)) = f-1(x'i, y'i) = P'i,
Precisamente, questa affinità trasforma punti della prima terna in punti della seconda. Per dimostrare che l'affinità A é unica, se ne considera un'altra e si verifica che esse coincidano.
Sia essa
A'
= (x'i, y'i)
Ogni affinità trasforma rette in rette, oppure l'immagine mediante un'affinità di una retta è anche una retta:
Sia r una retta e si considerino
P1 ≠ P2
Si osserva ora che:
A(r) retta
tenendo conto che
P'1 = A(P1), P'2 = A(P'2),
ed applicando la definizione di affinità e considerando l'equazione parametrica, fissato un sistema di riferimento
f(P1) = (x1, y1), f(P2) = (x2, y2), f(P) = (x, y)
T) x' = a11x + a12y + a13, y' = a21x + a22y + a23.
Si procurano ora le coordinate dei punti trasformati mediante l'affinità in P1 e P2.
Essendo
P'1 = A(P1), f(P'1) = f(A(P1)) = T(f(P1)) = T(x1, y1) = (x'1, y'1),
x'1 = a11x1 + a12y1 + a13, y'1 = a21x1 + a22y1 + a23,
quindi
f(P) = (x'2, y'2), x'2 = a11x2 + a12y2 + a13, y'1 = a21x2 + a22y2 + a23,
infine, se
P
Ora
f(A(P)) = T(x, y) = (x', y'),
x' = a11(x1 + (x2 - x1)t) + a12(y1 + (y2 - y1)t) + a13,
y' = a21(x1 + (x2 - x1)t) + a22(y1 + (y2 - y1)t) + a23,
da ciò segue
x' = x'1 + (x'2 - x'1)t, y' = y'1 + (y'2 - y'1)t,
allora
(A(P))
Ogni affinità conserva i rapporti semplici.
A
Si consideri il rapporto semplice (PP2P1) nei seguenti casi.
1) r = [P2, P1] non parallela all'asse y:
2) r = [P2, P1] non parallela all'asse x:
Siccome P è allineato con P2 e P1,
Quindi, in ogni caso, si può scrivere
(PP2P1) = t.
Si consideri ora il rapporto semplice (PP'2P'1) negli stessi casi precedenti.
1)' r' = [P'2, P'1] non parallela all'asse y:
2) r = [P'2, P'1] non parallela all'asse x:
Siccome P è allineato con P2 e P1,
Quindi, in ogni caso, si può scrivere
(PP'2P'1) = t.
In definitiva, come volevasi, si ha:
(PP2P1) = (PP'2P'1).
Equazione della retta trasformata
Siano
r) ax + by + c = 0, r') a'x + b'y + c' = 0,
siccome l'immagine di r è una retta, si ha un'equazione non nota.
Si devono cioè trovare le relazioni tra a ed a', b e b', c e c' mediante A = f-1Tf.
Supponendo che
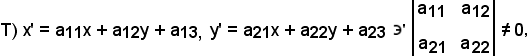
dire che r) è equazione della retta, vuol dire che
(x, y)
Siccome r' è trasformazione di r, segue
P' = A(P)
che sono note poichè si conosce A, e devono formare una soluzione di
a'x' + b'y' + c' = 0
Si è quindi trovato che (x, y) non solo è soluzione di ax + by + c = 0, ma anche di (*), quindi le due equazioni di primo grado sono equivalenti e pertanto
quindi, noti a, b, c, si possono determinare a', b', c', dando a ρ un valore arbitrario diverso da zero. Fissando ρ = 1, nelle prime due equazioni le incognite sono a' e b', e siccome c'è una combinazione lineare, si può calcolare l'unica soluzione di a' e b' che sostituite nella terza uguaglianza permettono di ricavare c'. Quindi, queste relazioni permettono di trovare l'equazione della retta trasformata.
Ogni affinità trasforma rette parallele in rette parallele
Si può anche dire che ogni affinità trasforma direzioni in direzioni.
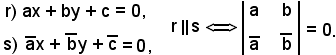
Si considerino ora le trasformate di r e di s indicate con
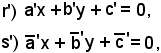
in modo che valgano ancora le relazioni precedenti.
Sotto tali ipotesi si vuole dimostrare che r'||s'.
Si considera il determinante suddetto, si moltiplica la prima riga per ρ e la seconda per σ, infine si sostituiscono i valori di ρa, ρb,

Pertanto risulta il prodotto di due determinanti uguale a zero e, poichè il secondo è diverso da zero, necessariamente è
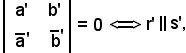
come volevasi dimostrare.