RETTE SUL PIANO ---> INDICE
Equazione della retta parallela all'asse x
Si consideri una retta parallela all'asse delle x e si indichi con Ux l'intersezione dell'asse y con la retta r, cioè
Qy = (asse y) r.
r.
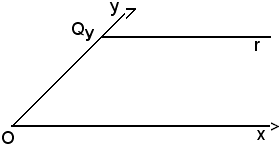
Se P r e Py è la sua proiezione sull'asse y, si ha:
r e Py è la sua proiezione sull'asse y, si ha:
Py = Qy,
quindi
 P
P r : Py = Qy.
r : Py = Qy.
Si supponga ora che nel punto Qy r sia parallela all'asse x, cioè
r || asse x in Qy,
e che Qy abbia ordinata h ed ascissa 0:
f(Qy) = (0, h).
Allora si ha che il punto P r ha una certa ascissa x ed ordinata uguale ad h.
r ha una certa ascissa x ed ordinata uguale ad h.
Se si indica con y l'ordinata del punto P, si ha:
 P
P r : f(P) = (x, y).
r : f(P) = (x, y).
Si deduce quindi che:
r || asse x y = h,
y = h,
cioè i punti della retta hanno come seconda coordinata y che soddisfa la condizione
y = h.
Si consideri ora un punto P del piano, si vuole dimostrare che:
P f(P) = (x, y), y = h
f(P) = (x, y), y = h  P
P r
r  r || asse x, f(Qy) = (0, h).
r || asse x, f(Qy) = (0, h).
Infatti, se si considera un punto P e si suppone che la sua seconda coordinata sia uguale ad h, ed inoltre se si considera la retta r parallela all'asse x, questa interseca l'asse y nel punto Qy avente ordinata h.
Quindi, la proprietà caratteristica della retta r è che l'equazione y = h è tale che soddisfi la seconda coordinata, essa si chiama equazione della retta parallela all'asse x.
Equazione della retta parallela all'asse y
sia soddisfatta soltanto dalle prime coordinate, essa si chiama equazione della retta parallela all'asse y.
Equazione della retta (non parallela agli assi x ed y)
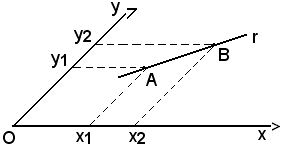
Si considerino due punti distinti A e B, che individuano una retta non parallela all'asse x ed all'asse y, rispettivamente di coordinate (x1, y1), (x2, y2).
La retta AB si indica
r[AB].
In altri termini,
r[AB] asse x, y1 ≠ y2,
asse x, y1 ≠ y2,
r[AB] asse y, x1 ≠ x2.
asse y, x1 ≠ x2.
Si può anche usare la seguente forma:
A(x1, y1) ≠ B(x2, y2),
inoltre i punti A e B non devono appartenere all'asse x ed all'asse y.
Prima di ricavare l'equazione della retta, si dimostra il seguente lemma:
-siano r ed r' due rette del piano, ed s un'altra retta non parallela ad esse; si dimostra che, se alla retta r si associa un punto A, la proiezione parallela ad s è una bigezione e conserva i rapporti semplici.
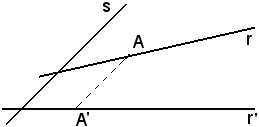
Si indica ora con p la proiezione parallela ad s del punto A di r su r', cioè
s r, s
r, s  r', è una bigezione che conserva i rapporti semplici.
r', è una bigezione che conserva i rapporti semplici.
Quanto ora espresso equivale a dire che
 A
A r,
r,  B
B r,
r,  C
C r, B ≠ C : (A B C) = (p(A) p(B) (C)).
r, B ≠ C : (A B C) = (p(A) p(B) (C)).
Ossia, ad ogni terna di punti A, B, C appartenenti alla retta r, tale che B sia diverso da C, risulta la terna ordinata di punti uguale alle proiezioni di A, B, C.
Quindi, si deve dimostrare tale relazione, nella quale per facilità d'interpretazione si pone
p(A) = A', p(B) = B', p(C) = C'.
A tal punto, si richiama il seguente postulato:
-considerate due rette r ed r', i punti A, B sulla retta r ed il punto C interno ad A e B, la proiezione di C sulla retta r', C', è interna alle proiezioni A' e B'.
Questo postulato mette in relazione il verso della retta r con quello della retta r', quindi si fissa un verso su r ed r', come indicato in figura.
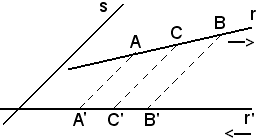
In tal modo, A precede C e C precede B sulla retta r, A' segue C' e C' segue B' sulla retta r'.
Si può quindi dire che questa è un'applicazione crescente o decrescente a seconda del verso di r'.
Attraverso questo postulato discende il teorema di Talete, il quale asserisce che
-in un fascio di rette tagliate da due trasversali, il rapporto dei segmenti staccati su una trasversale è uguale al rapporto dei segmenti staccati sull'altra.
Attraverso tale teorema ed il postulato precedente, considerando B ≠ C, si possono presentare i seguenti casi:
1) A interno a B, C A' interno a B', C', AC concorde con BC
A' interno a B', C', AC concorde con BC  A'C' concorde con B'C';
A'C' concorde con B'C';
2) B interno ad A, C B' interno ad A', C', AC concorde con BC
B' interno ad A', C', AC concorde con BC  A'C' concorde con B'C';
A'C' concorde con B'C';
3) C interno ad A, B C' interno ad A', B', AC concorde con BC
C' interno ad A', B', AC concorde con BC  A'C' concorde con B'C'.
A'C' concorde con B'C'.
Quindi, i valori ottenuti dalla proporzionalità sono:
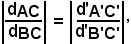
e dalle condizioni suddette si deduce che i rapporti in valore assoluto corrispondono a
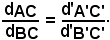
Dato che i segmenti AC e BC sono concordi, si ha
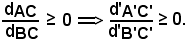
Se inoltre si verifica che
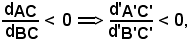
si conclude che i due rapporti sono uguali.
D'altronde, il primo rapporto delle due distanze rappresenta il rapporto semplice dei punti A, B, C, mentre il secondo rappresenta il rapporto semplice delle proiezioni nei punti A', B', C', cioè:
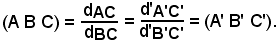
Quindi è stato dimostrato il lemma, cioè che anche le proiezioni dei punti conservano i rapporti semplici. Tale lemma si applica al teorema precedente.
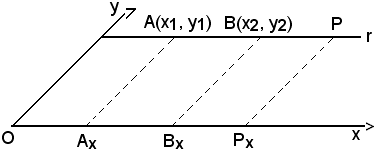
Allo scopo, si considerano le proiezioni, dai punti A e B della retta r, parallele all'asse x ed all'asse y, rispettivamente Ax, Bx, ed Ay, By, e poi quelle di un generico punto P di coordinate Px, Py.
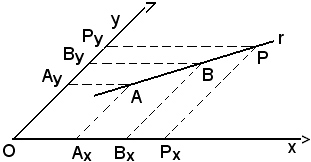
Per il lemma visto, si hanno le seguenti uguaglianze dei rapporti semplici:
(P B A) = (Px Bx Ax), (P B A) = (Py By Ay) (Px Bx Ax) = (Py By Ay).
(Px Bx Ax) = (Py By Ay).
Indicando
A(x1, y1), B(x2, y2), P(x, y),
le coordinate dei punti A, B, P, si ha:
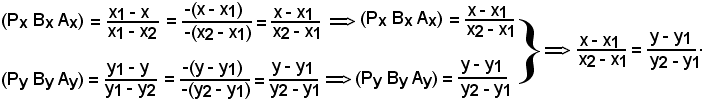
In conclusione, le coordinate del punto P della retta r costituiscono una soluzione dell'equazione
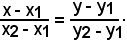
Quindi, si è visto che, fissato il riferimento (O, Ux, Uy) ed i punti A(x1, y1), B(x2, y2), con x1 ≠ x2 ed y1 ≠ y2, risulta:
(O, Ux, Uy) ed i punti A(x1, y1), B(x2, y2), con x1 ≠ x2 ed y1 ≠ y2, risulta:
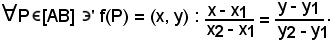
Pertanto, ogni soluzione di questa equazione è la coppia delle coordinate del punto P appartenente alla retta r. Se sono note le coordinate di P, cioè siano x ed y, si ha che il primo membro è uguale al secondo. A tal punto, si possono considerare i rapporti semplici relativi alle proiezioni dei punti P, B, A sull'asse x e sull'asse y, pertanto logicamente risulta che
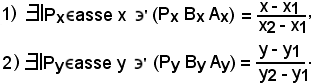
Si consideri ora sulla retta un punto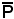 , quindi si ha che
, quindi si ha che
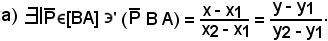
Se inoltre si considerano le rispettive proiezioni del punto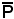 , rispettivamente sull'asse x e sull'asse y, per il lemma precedente si ha:
, rispettivamente sull'asse x e sull'asse y, per il lemma precedente si ha:
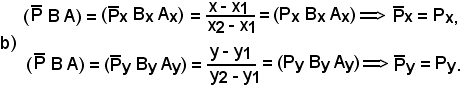
D'altronde, il punto Px rappresenta l'ascissa di x ed il punto Py l'ordinata di y.
Allora, il punto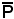 prescelto deve avere come ascissa l'ascissa di Px =
prescelto deve avere come ascissa l'ascissa di Px = 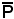 x nel riferimento OUx, e come ordinata l'ordinata di Py =
x nel riferimento OUx, e come ordinata l'ordinata di Py = 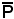 y nel riferimento OUy.
y nel riferimento OUy.
E' dimostrato quindi che il punto P appartiene alla retta r, cioè nell'equazione precedente le sue coordinate sono una soluzione.
Ciò detto, si possono scrivere tutte le equazioni alle quali corrispondono determinati punti.
Forma tipica dell'equazione di una retta
Si consideri l'equazione di una retta non parallela all'asse x ed all'asse y,
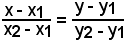
soddisfacente le condizioni
x1 ≠ x2, y1 ≠ y2, A ≠ B.
Si riduce l'equazione sotto forma intera, cioè:
(x - x1)(y2 - y1) = (y - y1)(x2 - x1),
x(y2 - y1) - x1y2 + x1y1 = y(x2 - x1) - x2y1 + x1y1,
x(y2 - y1) + y(x1 - x2) - x1y2 + x2y1 = 0.
Ponendo
a = y2 - y1, b = x1 - x2, c = - x1y2 + x2y1,
si ha:
ax + by + c = 0.
Per tale equazione si possono presentare i seguenti quattro casi:
1) a = 0, b ≠ 0 by + c = 0
by + c = 0  y = -c/b = costante,
y = -c/b = costante,
2) a ≠ 0, b = 0 ax + c = 0
ax + c = 0  x = -c/a = costante,
x = -c/a = costante,
3) a ≠ 0, b ≠ 0, c = 0 ax + by = 0,
ax + by = 0,
4) a ≠ 0, b ≠ 0, c ≠ 0 ax + by + c = 0.
ax + by + c = 0.
Nel caso 1), l'equazione y = -c/b rappresenta una retta parallela all'asse x, che interseca l'asse y in un punto che ha come ordinata -c/b e come ascissa 0.
Nel caso 2), l'equazione x = -c/a rappresenta una retta parallela all'asse y, che interseca l'asse x in un punto che ha come ascissa -c/a e come ordinata 0.
Nel caso 3), l'equazione ax + by = 0 rappresenta una retta passante per l'origine degli assi.
Si considerino i punti A(0, 0) e B(-b, a) e si osservi che tale retta non è parallela agli assi x ed y, perchè a ≠ 0 e -b ≠ 0, e che la sua equazione si può trovare con la formula generale
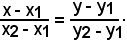
Infatti, sostituendo in tale formula
x1 = 0, y1 = 0, x2 = -b, y2 = a,
si ha:
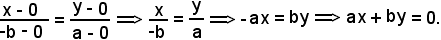
Nel caso 4), l'equazione ax + by + c = 0 rappresenta una retta non parallela agli assi x ed y e non passante per l'origine degli assi.
Si considerino i punti A(-c/a, 0) e B(0, -c/b), le cui coordinate hanno senso perchè a ≠ 0 e b ≠ 0, e quindi la sua equazione si può trovare con la formula generale
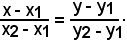
Infatti, sostituendo in tale formula
x1 = -c/a, y1 = 0, x2 = 0, y2 = -c/b,
si ha:
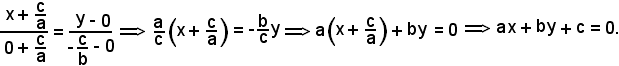
Si vuol vedere ora se due equazioni rappresentano la stessa retta r, della quale tutte le soluzioni sono sempre coppie ordinate.
Allo scopo, si considerino le equazioni
ax + by + c = 0, a'x + b'y + c' = 0.
Per rappresentare la stessa retta, le due equazioni devono essere uguali, il che vuol dire che esiste ρ ≠ 0 tale che a' = ρa, b' = ρb, c' = ρc, cioè
 ρ ≠ 0
ρ ≠ 0  a' = ρa, b' = ρb, c' = ρc.
a' = ρa, b' = ρb, c' = ρc.
Logicamente, risulta
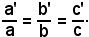
Quindi, se due diverse equazioni rappresentano la stessa retta, esse differiscono di un fattore di proporzionalità non nullo, pertanto le rette coincidono.
In definitiva, la determinazione di una retta non dipende da a, b e c, ma dalla terna seguente:
(ρa, ρb, ρc) .
Se si suppone a ≠ 0, dividendo ciascun termine della terna per ρa, si ha:
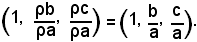
Da come si può notare, l'equazione della retta dipende esclusivamente dai rapporti b/a e c/a, in quanto il primo numero della terna è sempre 1.
Quindi, per fissare l'equazione della retta occorrono due numeri, b/a e c/a, e non 3.
Perciò, si dice che le rette del piano sono infinite a due, perchè la loro determinazione dipende dalla condizione di due valori.
Equazione parametrica della retta
Considerati la retta r ed un punto P r = [AB], si può considerare l'applicazione di r in R, e quindi ad ogni P si può associare t
r = [AB], si può considerare l'applicazione di r in R, e quindi ad ogni P si può associare t R,
t = (PBA). Questa applicazione è bigettiva perchè P appartiene alla
retta in un piano π ben determinato, e quindi si può considerare la sua
inversa, che in tal caso risulta:
R,
t = (PBA). Questa applicazione è bigettiva perchè P appartiene alla
retta in un piano π ben determinato, e quindi si può considerare la sua
inversa, che in tal caso risulta:
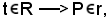
cioè c'è un elemento dei reali al quale corrisponde un punto appartenente alla retta.
Si vede ora come si esprimono analiticamente tale relazione e l'inversa della bigezione.
Si fissi t R e sia:
R e sia:
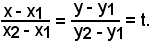
In definitiva, si può ottenere la seguente coppia:
(x = (x2 - x1)t + x1, y = (y2 - y1)t + y1),
nella quale x ed y sono le coordinate del punto P appartenente alla retta passante per A e B.
Si sono quindi ricavate le equazioni parametriche della retta r:
x = (x2 - x1)t + x1, y = (y2 - y1)t + y1,
nelle quali t è il parametro.
Questo ragionamento è stato fatto per la retta non parallela agli assi x ed y.
Si osserva ora che, se la retta è parallela all'asse x, A e B devono avere la stessa ordinata, cioè y1 = y2, mentre se la retta è parallela all'asse y, A e B devono avere la stessa ascissa, cioè x1 = x2.
Infatti, si considerino la retta r parallela all'asse x, due suoi punti A(x1, y1), B(x2, y2), ed un punto P avente la stessa ordinata di A e B ed ascissa

indicata con
x = (x2 - x1)t + x1.
E' quindi dimostrato che l'equazione precedente vale anche quando la retta r è parallela all'asse x.
Lo stesso ragionamento si fa anche quando la retta r è parallela all'asse y, pertanto vale:
y = (y2 - y1)t + y1.
In definitiva, le equazioni suddette valgono nel caso in cui la retta sia parallela all'asse x, all'asse y, oppure non parallela ai due assi. Pertanto, le equazioni possono considerarsi del tipo
x = αt + β,
y = γt + δ,
avendo posto
x2 - x1 = α, y2 - y1 = γ, x1 = β, y1 = δ,
con la condizione che
(α, β) ≠ (0, 0).
A tal punto, si vuol vedere se esiste nel piano una retta che ha, come equazioni, le prime due equazioni parametriche.
Si considerino nel piano i punti
A(β, δ), B(α + β, γ + δ).
Siccome α e γ non possono essere contemporaneamente nulli, non può accadere che A = B.
Applicando la formula, si ha
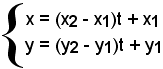
ed essendo
x1 = β, y1 = δ, x2 = α + β, y2 = γ + δ,
si ha:
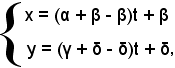
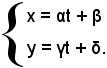
E' bene tener presente che al variare del parametro t variano le coppie dei punti, pertanto è verificato che la retta esiste ed ha le suddette come equazioni.
Se si cambiano i punti A e B, cioè si considerano altri punti della stessa retta, l'equazione è la stessa, e ciò può dedursi sostituendo a t il seguente valore:
t = at' + b,
pertanto si ha
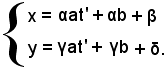
Rappresentazioni tipiche della retta
Supponendo che la retta sia individuata dai punti A(x1, y1) e B(x2, y2), essa ha un'equazione di primo grado del tipo seguente:
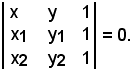
Infatti, il complemento algebrico di x è dato da:
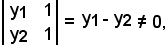
mentre quello di y è dato da
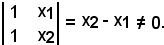
Quindi, essendo
x2 - x1 ≠ 0, y1 - y2 ≠ 0 x1 ≠ x2, y1 ≠ y2
x1 ≠ x2, y1 ≠ y2  A ≠ B.
A ≠ B.
A tal punto, si dimostra che il determinante suddetto, che rappresenta l'equazione della retta, è uguale a zero.
Infatti:
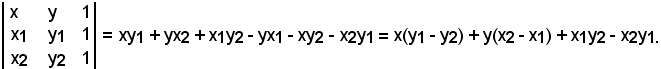
Siccome tale equazione dev'essere soddisfatta dalle coordinate del punto A, sostituendo nell'ultima uguaglianza x1 al posto di x ed y1 al posto di y, si ha:
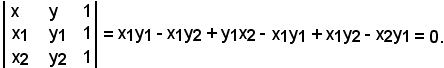
Siccome tale equazione dev'essere anche soddisfatta dalle coordinate del punto B, sostituendo nell'ultima uguaglianza x2 al posto di x ed y2 al posto di y, si perviene allo stesso risultato, cioè il determinante in questione è uguale a zero, come volevasi dimostrare.
Equazione segmentaria della retta
Sia r una retta che interseca gli assi x ed y, rispettivamente nei punti distinti P e Q, cioè:
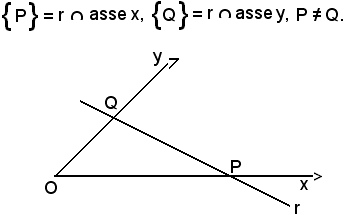
Sia
ax + by + c = 0
l'equazione della retta r, con c ≠ 0, cioè non soddisfatta dalla coppia (0, 0) e quindi non passante per l'origine.
Se si calcolano le coordinate del punto P appartenente all'asse x, l'ordinata è nulla, pertanto l'ascissa è uguale a -b/a. Analogamente, se si calcolano le coordinate del punto Q appartenente all'asse y, l'ascissa è nulla, pertanto l'ordinata è uguale a -c/b.
Moltiplicando ambo i membri dell'equazione per -1/c, si ha:
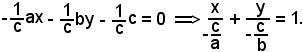
Ponendo
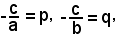
risulta
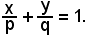
Questa è l'equazione segmentaria della retta r,
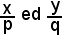
rappresentano le intercette della retta r rispettivamente sugli assi x ed y.
Rette coincidenti
Siano r ed r' due rette del piano π, rispettivamente di equazioni
ax + by + c = 0, a'x + b'y + c' = 0,
dire che che r = r', equivale a dire che la matrice dei coefficienti ha rango 1, cioè
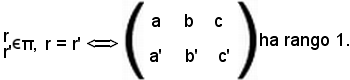
Se si considera il sistema formato dai coefficienti delle due equazioni della rette r ed r', si può introdurre il simbolo suddetto di matrice, che permette di formare un determinante. Tale matrice è formata da due righe e tre colonne e si può anche chiamare matrice 2 x 3 rango 1.
Inoltre è noto che un sistema ammette una soluzione quando il determinante dei coefficienti delle incognite è diverso da zero, cioè:
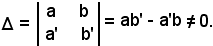
Si ricorda ora che dire che la matrice ha rango 1 equivale a dire che l'ordine massimo dei determinanti non tutti nulli che si possono estrarre dalla matrice è uguale ad 1.
Si dimostra che i determinanti del secondo ordine sono uguali a zero e si ottengono dalle prime due colonne tralasciando la terza:
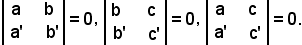
I determinanti di primo ordine si ottengono considerando una riga ed una colonna, cioè sono formati da un solo elemento:
|a| oppure |b|.
Quindi, si osserva che tutti i determinanti del secondo ordine sono nulli, ma ne esiste qualcuno di primo ordine che non lo è. Si tratta quindi di dimostrare che la proposizione geometrica equivale a quella analitica e viceversa, nell'ipotesi che la matrice ha rango 1.
Infatti, si considerano
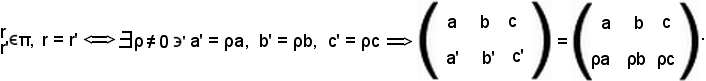
Esaminando la matrice, si può notare che tutti i determinanti del secondo ordine sono nulli, perchè
aρb - bρa = 0,
bρc - bcρ = 0,
cρa - aρc = 0,
quindi il rango della matrice non può essere 2, inoltre non può essere 0, perchè i coefficienti a, b, a' e b' sono diversi da zero, in quanto coefficienti di equazioni che rappresentano rispettivamente due rette. Pertanto c'è almeno un elemento di primo ordine e si può concludere che la matrice ha rango 1.
Viceversa, si suppone che la matrice
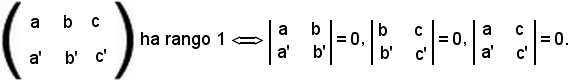
Si ha quindi:
ab' - a'b = 0,
bc' - b'c = 0,
ac' - a'c = 0.
Si considera ora la prima uguaglianza nelle incognite a' e b', sostituendo in essa (-b, a), si ha una prima soluzione in quanto risulta
a(-b) - ab = 0,
cioè
0 = 0.
Questa è soluzione dell'equazione nelle incognite a' e b', tutte le altre soluzioni sono del tipo
(-ρb, ρa),
in cui ρ è un numero reale diverso da zero.
Per tale considerazione, in riferimento alle tre uguaglianze,
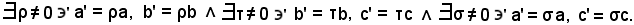
Essendo quindi
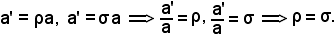
Essendo inoltre
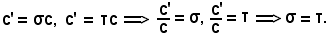
Avendo trovato
ρ = σ, σ = τ ρ = σ = τ.
ρ = σ = τ.
Pertanto,
 ρ ≠ 0
ρ ≠ 0  a' = ρa, b' = ρb, c' = ρc,
a' = ρa, b' = ρb, c' = ρc,
e quindi
r = r',
come volevasi dimostrare.
Analiticamente, quanto detto si può esprimere sotto la seguente forma:
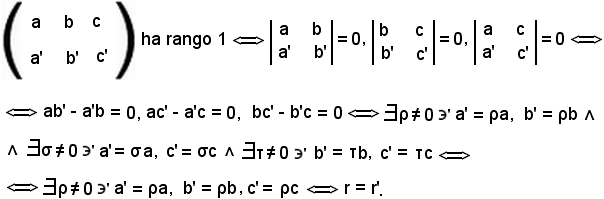
In definitiva, affinchè due rette siano coincidenti, la matrice deve avere rango 1.
Rette incidenti
Siano r ed r' due rette del piano π, rispettivamente di equazioni
ax + by + c = 0, con (a, b) ≠ (0, 0),
a'x + b'y + c' = 0, con (a', b') ≠ (0, 0).
Si dimostra che le due rette sono incidenti, cioè s'intersecano in un punto, ossia che il determinante del sistema, formato dalle due equazioni, ammette un determinante diverso da zero:
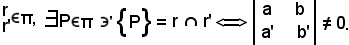
Infatti:
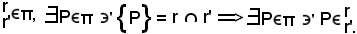
Si osserva ora che ogni punto della retta r ha una coppia di coordinate che soddisfano le equazioni di r ed r', pertanto
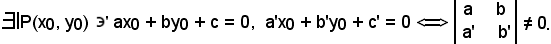
Si ha quindi che il sistema formato dalle due equazioni ammette un'unica soluzione, ed è dimostrato che esiste un solo punto P comune alle due rette. Si determinano ora le coordinate dell'unico punto comune alle due rette, che si ottengono dalla risoluzione del sistema formato dalle equazioni delle due rette:
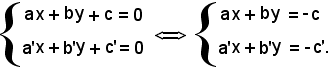
Risolvendo il sistema con il metodo di Cramer, si ha:
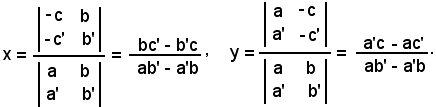
Nota bene
Nel caso delle rette incidenti, il rango della matrice dei coefficienti delle equazioni di r ed r' è uguale a 2.
Rette distinte e parallele
Le rette r ed r' non sono parallele, se
r = r', r r' ≠
r' ≠  .
.
Si suppone ora r ed r' parallele, cioè
r||r', r ≠ r' r
r  r' =
r' =  .
.
Si vuol vedere cosa accade per le equazioni delle due rette.
Siccome r ≠ r', il rango della matrice non può essere 1 e nemmeno 0, perchè si tratta di due equazioni con le condizioni (a, b) ≠ (0, 0), (a', b') ≠ (0, 0), quindi è 2 e non esiste nessun punto appartenente alle due rette.
Tutto ciò si traduce analiticamente nel fatto che non esiste nessuna coppia di numeri che soddisfa entrambe le equazioni di r ed r', quindi non esistono soluzioni, e ciò significa che il determinante dei coefficienti delle incognite è uguale a zero, cioè
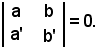
Si osservi inoltre che, siccome il rango della matrice è uguale a 2, esiste almeno un determinante estratto dalla matrice che è diverso da zero, cioè
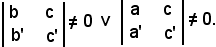
Però potrebbe accadere che un determinante è nullo e l'altro diverso da zero, e viceversa, oppure entrambi i determinanti diversi da zero.
Ricapitolando, se uno dei determinanti è diverso da zero, la matrice ha rango 2 ed il sistema è impossibile, quindi non esiste nessuna coppia di numeri che soddisfa le equazioni, pertanto le due rette non hanno alcun punto in comune, ed allora la loro intersezione è vuota.
Da quanto detto scaturisce la condizione di parallelismo delle due rette:
-se le due rette sono coincidenti, il rango della matrice è uguale ad 1, quindi i determinanti del secondo ordine sono nulli,
-se le due rette sono distinte, il rango della matrice è uguale a 2, pertanto
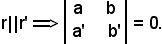
Questa è la condizione necessaria affinchè due rette siano parallele.
A tal punto, quando il determinante è uguale a zero, si deve considerare la matrice avente rango 2, cioè r r' =
r' =  , e quando la matrice ha rango 1, si ha r = r', cioè
, e quando la matrice ha rango 1, si ha r = r', cioè
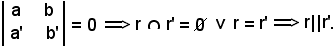
Questa è la condizione sufficiente affinchè due rette siano parallele:
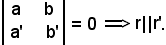
In definitiva, condizione necessaria e sufficiente affinchè due rette siano parallele è che il determinante dei coefficienti delle incognite delle equazioni delle rette r ed r' sia uguale a zero, cioè
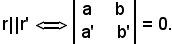
Nota bene
Il parallelismo coinvolge solo i termini noti quando
ab' - a'b = 0
 ρ≠0
ρ≠0  a' = ρa, b' = ρb.
a' = ρa, b' = ρb.
Quest'ultima condizione permette di dire che le equazionI di due rette fra loro parallele sono equivalenti a due equazioni che differiscono soltanto per il termine noto.
Quindi,
r||r'
 ρ≠0
ρ≠0  ax + by + c = 0, a'x + b'y + c' = 0
ax + by + c = 0, a'x + b'y + c' = 0  ax + by + c = 0, ρax + ρby + c' = 0.
ax + by + c = 0, ρax + ρby + c' = 0.
D'altronde, una retta può essere rappresentata da tante equazioni fra loro equivalenti, essendo polinomi che differiscono per un fattore di proporzionalità non nullo, pertanto si può moltiplicare primo e secondo membro per 1/ρ, ottenendo:
r||r' ax + by + c = 0, ax + by + c'' = 0,
ax + by + c = 0, ax + by + c'' = 0,
dove c'' = c'/ρ.
Queste due equazioni differiscono solo per il termine noto; viceversa, se si hanno due rette le cui equazioni differiscono al più per il termine noto, esse rappresentano due rette parallele.
Retta parallela ad una retta assegnata e passante per un punto
Siano r una retta di equazione
ax + by + c = 0
ed r' una retta parallela ad r e passante per un punto P(x0, y0).
Infatti, se la retta r' è parallela alla retta r, la sua equazione è del tipo
ax + by + c' = 0.
Inoltre, siccome r' passa per il punto P(x0, y0), le coordinate di P sono soluzioni di tale equazione, pertanto si ha:
ax0 + by0 + c' = 0 c' = -ax0 - by0.
c' = -ax0 - by0.
Sostituendo tale valore di c' nell'equazione ax + by + c' = 0, si ha:
ax + by - ax0 - by0 = 0 a(x - x0) + b(y - y0).
a(x - x0) + b(y - y0).
In definitiva, l'equazione della retta r' parallela alla retta r e passante per un punto P è:
a(x - x0) + b(y - y0).
Si consideri una retta parallela all'asse delle x e si indichi con Ux l'intersezione dell'asse y con la retta r, cioè
Qy = (asse y)

Se P
Py = Qy,
quindi
Si supponga ora che nel punto Qy r sia parallela all'asse x, cioè
r || asse x in Qy,
e che Qy abbia ordinata h ed ascissa 0:
f(Qy) = (0, h).
Allora si ha che il punto P
Se si indica con y l'ordinata del punto P, si ha:
Si deduce quindi che:
r || asse x
cioè i punti della retta hanno come seconda coordinata y che soddisfa la condizione
y = h.
Si consideri ora un punto P del piano, si vuole dimostrare che:
P
Infatti, se si considera un punto P e si suppone che la sua seconda coordinata sia uguale ad h, ed inoltre se si considera la retta r parallela all'asse x, questa interseca l'asse y nel punto Qy avente ordinata h.
Quindi, la proprietà caratteristica della retta r è che l'equazione y = h è tale che soddisfi la seconda coordinata, essa si chiama equazione della retta parallela all'asse x.
Equazione della retta parallela all'asse y
Analogamente, si dimostra che se una retta s è parallela all'asse y, essa interseca l'asse x in un punto Qy la
cui prima coordinata è k, allora tutti i punti della retta s hanno
prima coordinata k e seconda coordinata 0. Viceversa, ogni punto del piano
avente prima coordinata k appartiene alla retta s in modo che l'equazione
x = k
x = k
sia soddisfatta soltanto dalle prime coordinate, essa si chiama equazione della retta parallela all'asse y.
Equazione della retta (non parallela agli assi x ed y)
Si considerino due punti distinti A e B, che individuano una retta non parallela all'asse x ed all'asse y, rispettivamente di coordinate (x1, y1), (x2, y2).
La retta AB si indica
r[AB].

In altri termini,
r[AB]
r[AB]
Si può anche usare la seguente forma:
A(x1, y1) ≠ B(x2, y2),
inoltre i punti A e B non devono appartenere all'asse x ed all'asse y.
Prima di ricavare l'equazione della retta, si dimostra il seguente lemma:
-siano r ed r' due rette del piano, ed s un'altra retta non parallela ad esse; si dimostra che, se alla retta r si associa un punto A, la proiezione parallela ad s è una bigezione e conserva i rapporti semplici.

Si indica ora con p la proiezione parallela ad s del punto A di r su r', cioè
s
Quanto ora espresso equivale a dire che
Ossia, ad ogni terna di punti A, B, C appartenenti alla retta r, tale che B sia diverso da C, risulta la terna ordinata di punti uguale alle proiezioni di A, B, C.
Quindi, si deve dimostrare tale relazione, nella quale per facilità d'interpretazione si pone
p(A) = A', p(B) = B', p(C) = C'.
A tal punto, si richiama il seguente postulato:
-considerate due rette r ed r', i punti A, B sulla retta r ed il punto C interno ad A e B, la proiezione di C sulla retta r', C', è interna alle proiezioni A' e B'.
Questo postulato mette in relazione il verso della retta r con quello della retta r', quindi si fissa un verso su r ed r', come indicato in figura.

In tal modo, A precede C e C precede B sulla retta r, A' segue C' e C' segue B' sulla retta r'.
Si può quindi dire che questa è un'applicazione crescente o decrescente a seconda del verso di r'.
Attraverso questo postulato discende il teorema di Talete, il quale asserisce che
-in un fascio di rette tagliate da due trasversali, il rapporto dei segmenti staccati su una trasversale è uguale al rapporto dei segmenti staccati sull'altra.
Attraverso tale teorema ed il postulato precedente, considerando B ≠ C, si possono presentare i seguenti casi:
1) A interno a B, C
2) B interno ad A, C
3) C interno ad A, B
Quindi, i valori ottenuti dalla proporzionalità sono:
e dalle condizioni suddette si deduce che i rapporti in valore assoluto corrispondono a
Dato che i segmenti AC e BC sono concordi, si ha
Se inoltre si verifica che
si conclude che i due rapporti sono uguali.
D'altronde, il primo rapporto delle due distanze rappresenta il rapporto semplice dei punti A, B, C, mentre il secondo rappresenta il rapporto semplice delle proiezioni nei punti A', B', C', cioè:
Quindi è stato dimostrato il lemma, cioè che anche le proiezioni dei punti conservano i rapporti semplici. Tale lemma si applica al teorema precedente.
Allo scopo, si considerano le proiezioni, dai punti A e B della retta r, parallele all'asse x ed all'asse y, rispettivamente Ax, Bx, ed Ay, By, e poi quelle di un generico punto P di coordinate Px, Py.

Per il lemma visto, si hanno le seguenti uguaglianze dei rapporti semplici:
(P B A) = (Px Bx Ax), (P B A) = (Py By Ay)
Indicando
A(x1, y1), B(x2, y2), P(x, y),
le coordinate dei punti A, B, P, si ha:
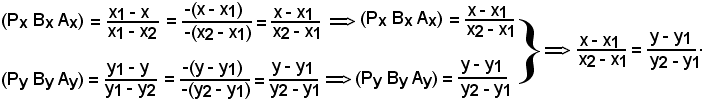
In conclusione, le coordinate del punto P della retta r costituiscono una soluzione dell'equazione
Quindi, si è visto che, fissato il riferimento
Pertanto, ogni soluzione di questa equazione è la coppia delle coordinate del punto P appartenente alla retta r. Se sono note le coordinate di P, cioè siano x ed y, si ha che il primo membro è uguale al secondo. A tal punto, si possono considerare i rapporti semplici relativi alle proiezioni dei punti P, B, A sull'asse x e sull'asse y, pertanto logicamente risulta che
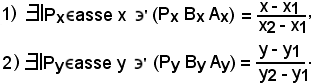
Si consideri ora sulla retta un punto
Se inoltre si considerano le rispettive proiezioni del punto
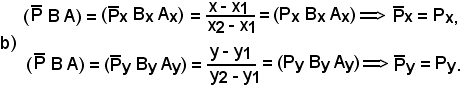
D'altronde, il punto Px rappresenta l'ascissa di x ed il punto Py l'ordinata di y.
Allora, il punto
E' dimostrato quindi che il punto P appartiene alla retta r, cioè nell'equazione precedente le sue coordinate sono una soluzione.
Ciò detto, si possono scrivere tutte le equazioni alle quali corrispondono determinati punti.
Forma tipica dell'equazione di una retta
Si consideri l'equazione di una retta non parallela all'asse x ed all'asse y,
soddisfacente le condizioni
x1 ≠ x2, y1 ≠ y2, A ≠ B.
Si riduce l'equazione sotto forma intera, cioè:
(x - x1)(y2 - y1) = (y - y1)(x2 - x1),
x(y2 - y1) - x1y2 + x1y1 = y(x2 - x1) - x2y1 + x1y1,
x(y2 - y1) + y(x1 - x2) - x1y2 + x2y1 = 0.
Ponendo
a = y2 - y1, b = x1 - x2, c = - x1y2 + x2y1,
si ha:
ax + by + c = 0.
Per tale equazione si possono presentare i seguenti quattro casi:
1) a = 0, b ≠ 0
2) a ≠ 0, b = 0
3) a ≠ 0, b ≠ 0, c = 0
4) a ≠ 0, b ≠ 0, c ≠ 0
Nel caso 1), l'equazione y = -c/b rappresenta una retta parallela all'asse x, che interseca l'asse y in un punto che ha come ordinata -c/b e come ascissa 0.
Nel caso 2), l'equazione x = -c/a rappresenta una retta parallela all'asse y, che interseca l'asse x in un punto che ha come ascissa -c/a e come ordinata 0.
Nel caso 3), l'equazione ax + by = 0 rappresenta una retta passante per l'origine degli assi.
Si considerino i punti A(0, 0) e B(-b, a) e si osservi che tale retta non è parallela agli assi x ed y, perchè a ≠ 0 e -b ≠ 0, e che la sua equazione si può trovare con la formula generale
Infatti, sostituendo in tale formula
x1 = 0, y1 = 0, x2 = -b, y2 = a,
si ha:
Nel caso 4), l'equazione ax + by + c = 0 rappresenta una retta non parallela agli assi x ed y e non passante per l'origine degli assi.
Si considerino i punti A(-c/a, 0) e B(0, -c/b), le cui coordinate hanno senso perchè a ≠ 0 e b ≠ 0, e quindi la sua equazione si può trovare con la formula generale
Infatti, sostituendo in tale formula
x1 = -c/a, y1 = 0, x2 = 0, y2 = -c/b,
si ha:
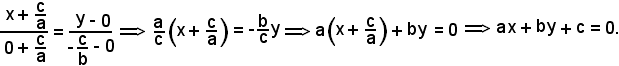
Si vuol vedere ora se due equazioni rappresentano la stessa retta r, della quale tutte le soluzioni sono sempre coppie ordinate.
Allo scopo, si considerino le equazioni
ax + by + c = 0, a'x + b'y + c' = 0.
Per rappresentare la stessa retta, le due equazioni devono essere uguali, il che vuol dire che esiste ρ ≠ 0 tale che a' = ρa, b' = ρb, c' = ρc, cioè
Logicamente, risulta
Quindi, se due diverse equazioni rappresentano la stessa retta, esse differiscono di un fattore di proporzionalità non nullo, pertanto le rette coincidono.
In definitiva, la determinazione di una retta non dipende da a, b e c, ma dalla terna seguente:
(ρa, ρb, ρc) .
Se si suppone a ≠ 0, dividendo ciascun termine della terna per ρa, si ha:
Da come si può notare, l'equazione della retta dipende esclusivamente dai rapporti b/a e c/a, in quanto il primo numero della terna è sempre 1.
Quindi, per fissare l'equazione della retta occorrono due numeri, b/a e c/a, e non 3.
Perciò, si dice che le rette del piano sono infinite a due, perchè la loro determinazione dipende dalla condizione di due valori.
Equazione parametrica della retta
Considerati la retta r ed un punto P
cioè c'è un elemento dei reali al quale corrisponde un punto appartenente alla retta.
Si vede ora come si esprimono analiticamente tale relazione e l'inversa della bigezione.
Si fissi t
In definitiva, si può ottenere la seguente coppia:
(x = (x2 - x1)t + x1, y = (y2 - y1)t + y1),
nella quale x ed y sono le coordinate del punto P appartenente alla retta passante per A e B.
Si sono quindi ricavate le equazioni parametriche della retta r:
x = (x2 - x1)t + x1, y = (y2 - y1)t + y1,
nelle quali t è il parametro.
Questo ragionamento è stato fatto per la retta non parallela agli assi x ed y.
Si osserva ora che, se la retta è parallela all'asse x, A e B devono avere la stessa ordinata, cioè y1 = y2, mentre se la retta è parallela all'asse y, A e B devono avere la stessa ascissa, cioè x1 = x2.
Infatti, si considerino la retta r parallela all'asse x, due suoi punti A(x1, y1), B(x2, y2), ed un punto P avente la stessa ordinata di A e B ed ascissa
indicata con
x = (x2 - x1)t + x1.

E' quindi dimostrato che l'equazione precedente vale anche quando la retta r è parallela all'asse x.
Lo stesso ragionamento si fa anche quando la retta r è parallela all'asse y, pertanto vale:
y = (y2 - y1)t + y1.
In definitiva, le equazioni suddette valgono nel caso in cui la retta sia parallela all'asse x, all'asse y, oppure non parallela ai due assi. Pertanto, le equazioni possono considerarsi del tipo
x = αt + β,
y = γt + δ,
avendo posto
x2 - x1 = α, y2 - y1 = γ, x1 = β, y1 = δ,
con la condizione che
(α, β) ≠ (0, 0).
A tal punto, si vuol vedere se esiste nel piano una retta che ha, come equazioni, le prime due equazioni parametriche.
Si considerino nel piano i punti
A(β, δ), B(α + β, γ + δ).
Siccome α e γ non possono essere contemporaneamente nulli, non può accadere che A = B.
Applicando la formula, si ha
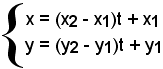
ed essendo
x1 = β, y1 = δ, x2 = α + β, y2 = γ + δ,
si ha:
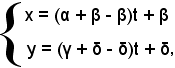
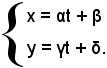
E' bene tener presente che al variare del parametro t variano le coppie dei punti, pertanto è verificato che la retta esiste ed ha le suddette come equazioni.
Se si cambiano i punti A e B, cioè si considerano altri punti della stessa retta, l'equazione è la stessa, e ciò può dedursi sostituendo a t il seguente valore:
t = at' + b,
pertanto si ha
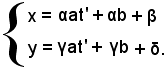
Rappresentazioni tipiche della retta
Supponendo che la retta sia individuata dai punti A(x1, y1) e B(x2, y2), essa ha un'equazione di primo grado del tipo seguente:
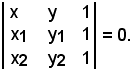
Infatti, il complemento algebrico di x è dato da:
mentre quello di y è dato da
Quindi, essendo
x2 - x1 ≠ 0, y1 - y2 ≠ 0
A tal punto, si dimostra che il determinante suddetto, che rappresenta l'equazione della retta, è uguale a zero.
Infatti:
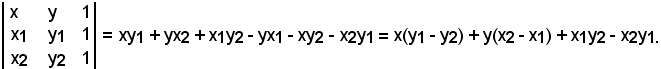
Siccome tale equazione dev'essere soddisfatta dalle coordinate del punto A, sostituendo nell'ultima uguaglianza x1 al posto di x ed y1 al posto di y, si ha:
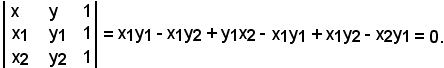
Siccome tale equazione dev'essere anche soddisfatta dalle coordinate del punto B, sostituendo nell'ultima uguaglianza x2 al posto di x ed y2 al posto di y, si perviene allo stesso risultato, cioè il determinante in questione è uguale a zero, come volevasi dimostrare.
Equazione segmentaria della retta
Sia r una retta che interseca gli assi x ed y, rispettivamente nei punti distinti P e Q, cioè:

Sia
ax + by + c = 0
l'equazione della retta r, con c ≠ 0, cioè non soddisfatta dalla coppia (0, 0) e quindi non passante per l'origine.
Se si calcolano le coordinate del punto P appartenente all'asse x, l'ordinata è nulla, pertanto l'ascissa è uguale a -b/a. Analogamente, se si calcolano le coordinate del punto Q appartenente all'asse y, l'ascissa è nulla, pertanto l'ordinata è uguale a -c/b.
Moltiplicando ambo i membri dell'equazione per -1/c, si ha:
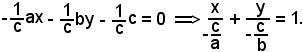
Ponendo
risulta
Questa è l'equazione segmentaria della retta r,
rappresentano le intercette della retta r rispettivamente sugli assi x ed y.
Rette coincidenti
Siano r ed r' due rette del piano π, rispettivamente di equazioni
ax + by + c = 0, a'x + b'y + c' = 0,
dire che che r = r', equivale a dire che la matrice dei coefficienti ha rango 1, cioè

Se si considera il sistema formato dai coefficienti delle due equazioni della rette r ed r', si può introdurre il simbolo suddetto di matrice, che permette di formare un determinante. Tale matrice è formata da due righe e tre colonne e si può anche chiamare matrice 2 x 3 rango 1.
Inoltre è noto che un sistema ammette una soluzione quando il determinante dei coefficienti delle incognite è diverso da zero, cioè:
Si ricorda ora che dire che la matrice ha rango 1 equivale a dire che l'ordine massimo dei determinanti non tutti nulli che si possono estrarre dalla matrice è uguale ad 1.
Si dimostra che i determinanti del secondo ordine sono uguali a zero e si ottengono dalle prime due colonne tralasciando la terza:
I determinanti di primo ordine si ottengono considerando una riga ed una colonna, cioè sono formati da un solo elemento:
|a| oppure |b|.
Quindi, si osserva che tutti i determinanti del secondo ordine sono nulli, ma ne esiste qualcuno di primo ordine che non lo è. Si tratta quindi di dimostrare che la proposizione geometrica equivale a quella analitica e viceversa, nell'ipotesi che la matrice ha rango 1.
Infatti, si considerano
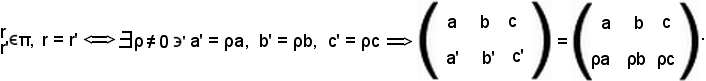
Esaminando la matrice, si può notare che tutti i determinanti del secondo ordine sono nulli, perchè
aρb - bρa = 0,
bρc - bcρ = 0,
cρa - aρc = 0,
quindi il rango della matrice non può essere 2, inoltre non può essere 0, perchè i coefficienti a, b, a' e b' sono diversi da zero, in quanto coefficienti di equazioni che rappresentano rispettivamente due rette. Pertanto c'è almeno un elemento di primo ordine e si può concludere che la matrice ha rango 1.
Viceversa, si suppone che la matrice
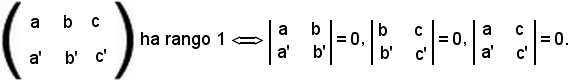
Si ha quindi:
ab' - a'b = 0,
bc' - b'c = 0,
ac' - a'c = 0.
Si considera ora la prima uguaglianza nelle incognite a' e b', sostituendo in essa (-b, a), si ha una prima soluzione in quanto risulta
a(-b) - ab = 0,
cioè
0 = 0.
Questa è soluzione dell'equazione nelle incognite a' e b', tutte le altre soluzioni sono del tipo
(-ρb, ρa),
in cui ρ è un numero reale diverso da zero.
Per tale considerazione, in riferimento alle tre uguaglianze,
Essendo quindi
Essendo inoltre
Avendo trovato
ρ = σ, σ = τ
Pertanto,
e quindi
r = r',
come volevasi dimostrare.
Analiticamente, quanto detto si può esprimere sotto la seguente forma:
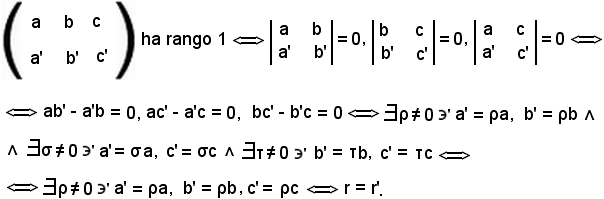
In definitiva, affinchè due rette siano coincidenti, la matrice deve avere rango 1.
Rette incidenti
Siano r ed r' due rette del piano π, rispettivamente di equazioni
ax + by + c = 0, con (a, b) ≠ (0, 0),
a'x + b'y + c' = 0, con (a', b') ≠ (0, 0).
Si dimostra che le due rette sono incidenti, cioè s'intersecano in un punto, ossia che il determinante del sistema, formato dalle due equazioni, ammette un determinante diverso da zero:
Infatti:
Si osserva ora che ogni punto della retta r ha una coppia di coordinate che soddisfano le equazioni di r ed r', pertanto
Si ha quindi che il sistema formato dalle due equazioni ammette un'unica soluzione, ed è dimostrato che esiste un solo punto P comune alle due rette. Si determinano ora le coordinate dell'unico punto comune alle due rette, che si ottengono dalla risoluzione del sistema formato dalle equazioni delle due rette:
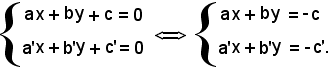
Risolvendo il sistema con il metodo di Cramer, si ha:
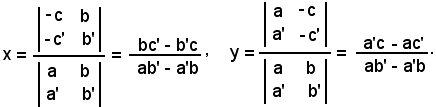
Nota bene
Nel caso delle rette incidenti, il rango della matrice dei coefficienti delle equazioni di r ed r' è uguale a 2.
Rette distinte e parallele
Le rette r ed r' non sono parallele, se
r = r', r
Si suppone ora r ed r' parallele, cioè
r||r', r ≠ r'
Si vuol vedere cosa accade per le equazioni delle due rette.
Siccome r ≠ r', il rango della matrice non può essere 1 e nemmeno 0, perchè si tratta di due equazioni con le condizioni (a, b) ≠ (0, 0), (a', b') ≠ (0, 0), quindi è 2 e non esiste nessun punto appartenente alle due rette.
Tutto ciò si traduce analiticamente nel fatto che non esiste nessuna coppia di numeri che soddisfa entrambe le equazioni di r ed r', quindi non esistono soluzioni, e ciò significa che il determinante dei coefficienti delle incognite è uguale a zero, cioè
Si osservi inoltre che, siccome il rango della matrice è uguale a 2, esiste almeno un determinante estratto dalla matrice che è diverso da zero, cioè
Però potrebbe accadere che un determinante è nullo e l'altro diverso da zero, e viceversa, oppure entrambi i determinanti diversi da zero.
Ricapitolando, se uno dei determinanti è diverso da zero, la matrice ha rango 2 ed il sistema è impossibile, quindi non esiste nessuna coppia di numeri che soddisfa le equazioni, pertanto le due rette non hanno alcun punto in comune, ed allora la loro intersezione è vuota.
Da quanto detto scaturisce la condizione di parallelismo delle due rette:
-se le due rette sono coincidenti, il rango della matrice è uguale ad 1, quindi i determinanti del secondo ordine sono nulli,
-se le due rette sono distinte, il rango della matrice è uguale a 2, pertanto
Questa è la condizione necessaria affinchè due rette siano parallele.
A tal punto, quando il determinante è uguale a zero, si deve considerare la matrice avente rango 2, cioè r
Questa è la condizione sufficiente affinchè due rette siano parallele:
In definitiva, condizione necessaria e sufficiente affinchè due rette siano parallele è che il determinante dei coefficienti delle incognite delle equazioni delle rette r ed r' sia uguale a zero, cioè
Nota bene
Il parallelismo coinvolge solo i termini noti quando
ab' - a'b = 0
Quest'ultima condizione permette di dire che le equazionI di due rette fra loro parallele sono equivalenti a due equazioni che differiscono soltanto per il termine noto.
Quindi,
r||r'
D'altronde, una retta può essere rappresentata da tante equazioni fra loro equivalenti, essendo polinomi che differiscono per un fattore di proporzionalità non nullo, pertanto si può moltiplicare primo e secondo membro per 1/ρ, ottenendo:
r||r'
dove c'' = c'/ρ.
Queste due equazioni differiscono solo per il termine noto; viceversa, se si hanno due rette le cui equazioni differiscono al più per il termine noto, esse rappresentano due rette parallele.
Retta parallela ad una retta assegnata e passante per un punto
Siano r una retta di equazione
ax + by + c = 0
ed r' una retta parallela ad r e passante per un punto P(x0, y0).
Infatti, se la retta r' è parallela alla retta r, la sua equazione è del tipo
ax + by + c' = 0.
Inoltre, siccome r' passa per il punto P(x0, y0), le coordinate di P sono soluzioni di tale equazione, pertanto si ha:
ax0 + by0 + c' = 0
Sostituendo tale valore di c' nell'equazione ax + by + c' = 0, si ha:
ax + by - ax0 - by0 = 0
In definitiva, l'equazione della retta r' parallela alla retta r e passante per un punto P è:
a(x - x0) + b(y - y0).