RIFERIMENTI E PIANI NELLO SPAZIO ---> INDICE
Si considerino lo spazio euclideo e le proprietà d'incidenza e di parallelismo, cercando di associare ad ogni punto una terna di numeri reali.
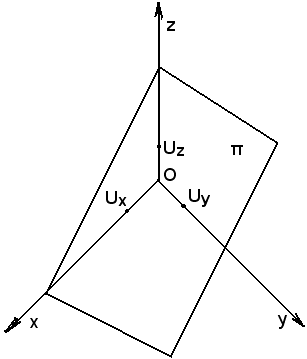
Si chiama riferimento nello spazio ogni quaterna di punti (O, Ux, Uy, Uz) tale che i quattro punti non appartengano ad uno stesso piano.
Tale riferimento s'indica con (O, Ux, Uy, Uz).
(O, Ux, Uy, Uz).
Si osserva ora che:
-tre punti definiscono un piano e l'altro non gli appartiene;
-O si chiama punto origine;
-Ux si chiama punto dell'asse delle x;
-Uy si chiama punto dell'asse delle y;
-Uz si chiama punto dell'asse delle z;
-la retta [O, Ux] si chiama asse delle x;
-la retta [O, Uy] si chiama asse delle y;
-la retta [O, Uz] si chiama asse delle z.
Si osserva inoltre che le tre rette sono complanari, pur essendo concorrenti nello stesso punto.
Fissato un riferimento, si può stabilire una bigezione dello spazio nell'insieme delle terne ordinate di numeri reali.
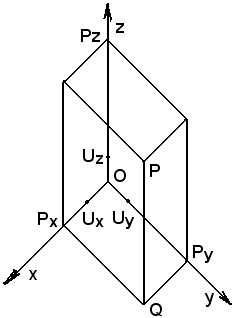
Si consideri un punto P e da esso si tracci il piano parallelo a quello formato dall'asse delle x e dall'asse delle z. Tale piano interseca l'asse delle x nel punto Px.
Analogamente si ragiona per le altre proiezioni Py e Pz.
I punti Px, Py e Pz appartengono rispettivamente agli assi delle x, delle y e delle z, su cui è fissato il riferimento.
Siccome dal punto P sono state ottenute Px, Py e Pz, ad esse si associano rispettivamente l'ascissa x del punto rispetto al riferimento (O, Ux), l'ordinata y del punto rispetto al riferimento
(O, Ux), l'ordinata y del punto rispetto al riferimento  (O, Uy) e la quota z del punto rispetto al riferimento
(O, Uy) e la quota z del punto rispetto al riferimento  (O, Uz).
(O, Uz).
Si è così ottenuta l'applicazione bigettiva
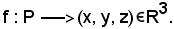
Ora si osserva che:
x è l'ascissa del punto P;
y è l'ordinata del punto P;
z è la quota del punto P;
(x, y, z) è la terna delle coordinate del punto P rispetto al riferimento .
.
Se da Ux si traccia il piano parallelo agli assi delle y e delle z, da Uy quello parallelo agli assi delle x e delle y e da Uz quello parallelo agli assi delle x e delle z, si ha il punto unità U del riferimento, U(1, 1, 1). Le coordinate del punto origine O sono tutte nulle, cioè O(0, 0, 0).
Inoltre, a

Se ora si considera il piano formato dagli assi x ed y, esso si indica con [x, y] = πxy e si chiama piano coordinato xy.
Analogamente, [y, z] = πyz e si chiama piano coordinato yz, infine [x, z] = πxz e si chiama piano coordinato xz.
Se
P πxy,
πxy,
e se da P si traccia il piano parallelo allo stesso piano, si ha sempre lo stesso piano, quindi la quota z = 0.
Se
P πxz,
πxz,
e se da P si traccia il piano parallelo allo stesso piano, si ha sempre lo stesso piano, quindi l'ordinata y = 0.
Se
P πyz,
πyz,
e se da P si traccia il piano parallelo allo stesso piano, si ha sempre lo stesso piano, quindi l'ascissa x = 0.
Quindi,
P πxy
πxy  P(x, y, 0),
P(x, y, 0),
P πxz
πxz  P(x, 0, z),
P(x, 0, z),
P πyz
πyz  P(0, y, z).
P(0, y, z).
Rappresentazione analitica dei piani nello spazio
Il piano π || πxy è rappresentato nella figura seguente.
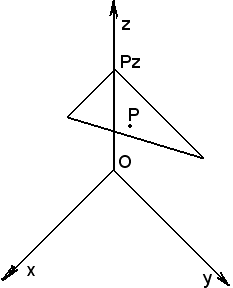
Preso un punto P π, il piano ottenuto interseca l'asse delle z nel punto Pz e nel riferimento
π, il piano ottenuto interseca l'asse delle z nel punto Pz e nel riferimento  (O, Uz) ha una certa quota h.
(O, Uz) ha una certa quota h.
Ovviamente, tutti i punti del piano hanno sempre quota uguale ad h, cioè se
P π
π  z = h.
z = h.
Si può quindi dire che: i punti del piano parallelo al piano xy hanno coordinate soddisfacenti l'equazione z = h.
Analogamente, si possono procurare le equazioni dei piani paralleli agli altri due assi e si può osservare quindi che:
π || πxy z = h,
z = h,
π || πxz y = k,
y = k,
π || πyz x = l.
x = l.
Piani paralleli ad un solo asse
Si consideri un piano parallelo all'asse delle z, indicato nella seguente figura.
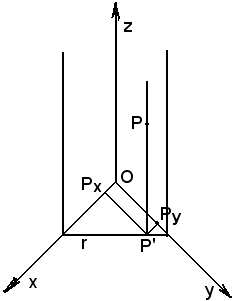
Tale piano taglia il piano coordinato πxy in una certa retta r.
Se sul piano πxy è fissato un riferimento, la retta r rispetto ad (O, Ux, Uy) ha equazione
(O, Ux, Uy) ha equazione
ax + by + d = 0,
con a e b non contemporaneamente nulli, poichè la traccia non può essere parallela né all'asse x né all'asse y.
Si consideri un punto P del piano e si supponga di determinare le sue coordinate.
Si traccino i due piani paralleli all'asse z e quindi una retta parallela all'asse z, cioè la PP' appartenente al piano considerato, pertanto
P' r.
r.
Se
P(x, y, z) P'(x, y, 0).
P'(x, y, 0).
Inoltre,
P(x, y, z) ax + by + d = 0.
ax + by + d = 0.
Cioè, se
π || asse z, P π
π  P(x, y, z)
P(x, y, z)  ax + by + d = 0.
ax + by + d = 0.
Analogamente, per gli altri piani si ha:
Si chiama riferimento nello spazio ogni quaterna di punti (O, Ux, Uy, Uz) tale che i quattro punti non appartengano ad uno stesso piano.
Tale riferimento s'indica con
Si osserva ora che:
-tre punti definiscono un piano e l'altro non gli appartiene;
-O si chiama punto origine;
-Ux si chiama punto dell'asse delle x;
-Uy si chiama punto dell'asse delle y;
-Uz si chiama punto dell'asse delle z;
-la retta [O, Ux] si chiama asse delle x;
-la retta [O, Uy] si chiama asse delle y;
-la retta [O, Uz] si chiama asse delle z.
Si osserva inoltre che le tre rette sono complanari, pur essendo concorrenti nello stesso punto.
Fissato un riferimento, si può stabilire una bigezione dello spazio nell'insieme delle terne ordinate di numeri reali.
Si consideri un punto P e da esso si tracci il piano parallelo a quello formato dall'asse delle x e dall'asse delle z. Tale piano interseca l'asse delle x nel punto Px.
Analogamente si ragiona per le altre proiezioni Py e Pz.
I punti Px, Py e Pz appartengono rispettivamente agli assi delle x, delle y e delle z, su cui è fissato il riferimento.
Siccome dal punto P sono state ottenute Px, Py e Pz, ad esse si associano rispettivamente l'ascissa x del punto rispetto al riferimento

Si è così ottenuta l'applicazione bigettiva
Ora si osserva che:
x è l'ascissa del punto P;
y è l'ordinata del punto P;
z è la quota del punto P;
(x, y, z) è la terna delle coordinate del punto P rispetto al riferimento
Se da Ux si traccia il piano parallelo agli assi delle y e delle z, da Uy quello parallelo agli assi delle x e delle y e da Uz quello parallelo agli assi delle x e delle z, si ha il punto unità U del riferimento, U(1, 1, 1). Le coordinate del punto origine O sono tutte nulle, cioè O(0, 0, 0).
Inoltre, a

Se ora si considera il piano formato dagli assi x ed y, esso si indica con [x, y] = πxy e si chiama piano coordinato xy.
Analogamente, [y, z] = πyz e si chiama piano coordinato yz, infine [x, z] = πxz e si chiama piano coordinato xz.
Se
P
e se da P si traccia il piano parallelo allo stesso piano, si ha sempre lo stesso piano, quindi la quota z = 0.
Se
P
e se da P si traccia il piano parallelo allo stesso piano, si ha sempre lo stesso piano, quindi l'ordinata y = 0.
Se
P
e se da P si traccia il piano parallelo allo stesso piano, si ha sempre lo stesso piano, quindi l'ascissa x = 0.
Quindi,
P
P
P
Rappresentazione analitica dei piani nello spazio
Il piano π || πxy è rappresentato nella figura seguente.

Preso un punto P
Ovviamente, tutti i punti del piano hanno sempre quota uguale ad h, cioè se
P
Si può quindi dire che: i punti del piano parallelo al piano xy hanno coordinate soddisfacenti l'equazione z = h.
Analogamente, si possono procurare le equazioni dei piani paralleli agli altri due assi e si può osservare quindi che:
π || πxy
π || πxz
π || πyz
Piani paralleli ad un solo asse
Si consideri un piano parallelo all'asse delle z, indicato nella seguente figura.

Tale piano taglia il piano coordinato πxy in una certa retta r.
Se sul piano πxy è fissato un riferimento, la retta r rispetto ad
ax + by + d = 0,
con a e b non contemporaneamente nulli, poichè la traccia non può essere parallela né all'asse x né all'asse y.
Si consideri un punto P del piano e si supponga di determinare le sue coordinate.
Si traccino i due piani paralleli all'asse z e quindi una retta parallela all'asse z, cioè la PP' appartenente al piano considerato, pertanto
P'
Se
P(x, y, z)
Inoltre,
P(x, y, z)
Cioè, se
π || asse z, P
Analogamente, per gli altri piani si ha:
π || asse y, P π
π  P(x, y, z)
P(x, y, z)  ax + cz + d = 0.
ax + cz + d = 0.
π || asse x, P π
π  P(x, y, z)
P(x, y, z)  by + cz + d = 0.
by + cz + d = 0.
π || asse x, P
Piano non parallelo ad alcun asse
Si considerino i tre assi x, y, z ed un piano non parallelo ad essi, quindi basta considerare due intersezioni che il piano ha con il piano coordinato.
Se il piano è determinato, è determinata la retta PQ.
Sia
π [O, Ux],
[O, Ux],
π [O, Uy],
[O, Uy],
π [O, Uz],
[O, Uz],
inoltre
π πxy = retta [PQ] di equazione ax + by + d = 0, (a, b) ≠ (0, 0),
πxy = retta [PQ] di equazione ax + by + d = 0, (a, b) ≠ (0, 0),
π πyz = retta [QR] di equazione b'y + c'z + d' = 0, (b', c') ≠ (0, 0),
πyz = retta [QR] di equazione b'y + c'z + d' = 0, (b', c') ≠ (0, 0),
in
 (O, Ux, Uy)
(O, Ux, Uy)
e rispettivamente in
 (O, Uy, Uz).
(O, Uy, Uz).
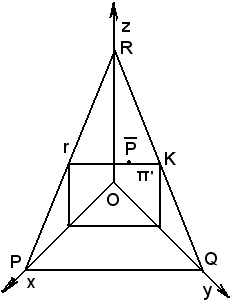
Si osserva ora che le coordinate di Q si ottengono sostituendo x = 0 nell'equazione ax + by + d = 0, ed anche z = 0 nell'equazione b'y + c'z + d' = 0, ottenendo così:
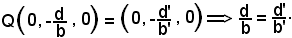
Considerando
d = d', b = b',
se
b' = ρb, d' = ρd, c' = ρc,
sostituendo nell'equazione
b'y + c'z + d' = 0,
si ha:
ρby + ρcz + ρd = 0,
cioè
by + cz + d = 0.
Si consideri un punto
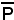 (
(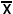 ,
, 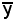 ,
, 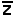 )
) π
π
e da esso si tracci il piano parallelo all'asse z ed alla retta PQ:

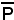
 π'
π'  π' || [PQ], π' || [O, Uz]
π' || [PQ], π' || [O, Uz]  π'
π'  πxy || [PQ]
πxy || [PQ]  π' di equazione ax + by + d = 0.
π' di equazione ax + by + d = 0.
Siccome
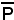
 π'
π'  a
a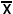 + b
+ b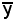 + d = 0.
+ d = 0.
Si consideri ora
π''
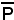
 π''
π''  π'' || πxy, z =
π'' || πxy, z = 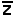 , r = π'
, r = π'  π'',
π'',
esso contiene P ed è rappresentato dal sistema
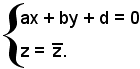
Si osserva ora che r è una retta di π che interseca πxz in un punto di PQ.
Siccome
r π
π  {K} = r
{K} = r  πyz
πyz  K
K [QR]
[QR]  K
K πyz,
πyz,
quindi la sua ascissa è uguale a zero e la sua ordinata y e la sua quota z devono soddisfare il sistema precedente, e dalla risoluzione di quest'ultimo, si ha:
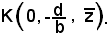
Siccome
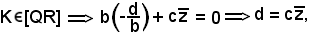
quindi
a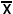 + b
+ b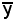 + c
+ c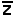 = 0.
= 0.
Condizioni di parallelismo e di coicidenza
E' noto che considerati due piani π e π', rispettivamente di equazioni
ax + by + cz + d = 0, a'x + b'y + c'z + d' = 0,
risulta che
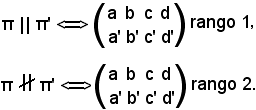
Se
π || π' π = π' v π
π = π' v π  π' =
π' =  .
.
Se

Siccome i due piani sono paralleli o incidenti lungo una retta, si può subito dedurre che se
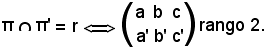
Piano parallelo ad un piano passante per un punto
Sia π un piano di equazione
ax + by + cz + d = 0, π || π' P0(x0, y0, z0)
P0(x0, y0, z0) π' : a(x - x0) + b(y - y0) + c(z - z0) = 0,
π' : a(x - x0) + b(y - y0) + c(z - z0) = 0,
in cui a, b, c sono uguali a quelli di un'equazione del piano π, quindi π || π', d'altronde passa per P0, e siccome P0 soddisfa l'equazione, si può dire che quella è l'equazione in questione.
Se π e π' sono due piani paralleli, le due equazioni possono differire al più per il termine noto.
Infatti
π || π'
 ρ≠0
ρ≠0  a' = ρa, b' = ρb, c' = ρc,
a' = ρa, b' = ρb, c' = ρc,
quindi l'equazione si può scrivere
ρax + ρby + ρcz + d' = 0.
Moltiplicando ambo i membri per 1/ρ, si ottiene l'equazione che rappresenta π':
ax + by + cz + d'/ρ = 0.
Le due equazioni possono differire al più per il termine noto.
Si considerino i tre assi x, y, z ed un piano non parallelo ad essi, quindi basta considerare due intersezioni che il piano ha con il piano coordinato.

Se il piano è determinato, è determinata la retta PQ.
Sia
π
π
π
inoltre
π
π
in
e rispettivamente in

Si osserva ora che le coordinate di Q si ottengono sostituendo x = 0 nell'equazione ax + by + d = 0, ed anche z = 0 nell'equazione b'y + c'z + d' = 0, ottenendo così:
Considerando
d = d', b = b',
se
b' = ρb, d' = ρd, c' = ρc,
sostituendo nell'equazione
b'y + c'z + d' = 0,
si ha:
ρby + ρcz + ρd = 0,
cioè
by + cz + d = 0.
Si consideri un punto
e da esso si tracci il piano parallelo all'asse z ed alla retta PQ:
Siccome
Si consideri ora
π''
esso contiene P ed è rappresentato dal sistema
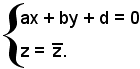
Si osserva ora che r è una retta di π che interseca πxz in un punto di PQ.
Siccome
r
quindi la sua ascissa è uguale a zero e la sua ordinata y e la sua quota z devono soddisfare il sistema precedente, e dalla risoluzione di quest'ultimo, si ha:
Siccome
quindi
a
Condizioni di parallelismo e di coicidenza
E' noto che considerati due piani π e π', rispettivamente di equazioni
ax + by + cz + d = 0, a'x + b'y + c'z + d' = 0,
risulta che
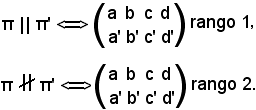
Se
π || π'
Se

mentre se
π π' =
π' =  ,
,
il sistema formato dalle equazioni dei due piani non ha soluzioni ed i ranghi delle due matrici sono diversi, e precisamente:
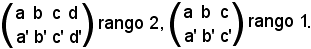
In definitiva, se
π || π',
la matrice
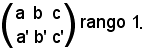
Tale condizione, oltre ad essere necessaria, come s'è visto, risulta sufficiente, infatti supponiamo:
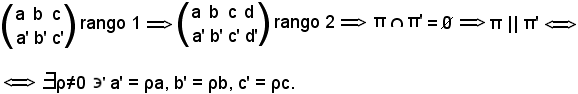
π
il sistema formato dalle equazioni dei due piani non ha soluzioni ed i ranghi delle due matrici sono diversi, e precisamente:
In definitiva, se
π || π',
la matrice
Tale condizione, oltre ad essere necessaria, come s'è visto, risulta sufficiente, infatti supponiamo:
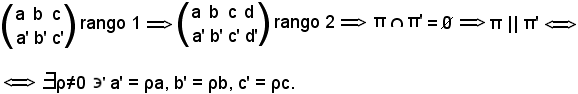
Siccome i due piani sono paralleli o incidenti lungo una retta, si può subito dedurre che se
Piano parallelo ad un piano passante per un punto
Sia π un piano di equazione
ax + by + cz + d = 0, π || π'
in cui a, b, c sono uguali a quelli di un'equazione del piano π, quindi π || π', d'altronde passa per P0, e siccome P0 soddisfa l'equazione, si può dire che quella è l'equazione in questione.
Se π e π' sono due piani paralleli, le due equazioni possono differire al più per il termine noto.
Infatti
π || π'
quindi l'equazione si può scrivere
ρax + ρby + ρcz + d' = 0.
Moltiplicando ambo i membri per 1/ρ, si ottiene l'equazione che rappresenta π':
ax + by + cz + d'/ρ = 0.
Le due equazioni possono differire al più per il termine noto.