RIFERIMENTI SUL PIANO ---> INDICE
Si considerino il piano euclideo e due rette distinte non parallele, indicando la prima con asse delle x e la seconda con asse delle y. Si consideri poi un punto unità non appartenente né all'asse x né all'asse y.
La terna formata dall'asse x, dall'asse y e dal punto U si chiama riferimento sul piano euclideo.

Si considerino ora le parallele per U all'asse x ed all'asse y, si ottengono pertanto due intersezioni, una sull'asse x, Ux, l'altra sull'asse y, Uy.
Ux ed Uy rappresentano i punti unità dell'asse x e dell'asse y.
Il punto di intersezione dell'asse x e dell'asse y si chiama origine e si indica con O.
Il riferimento formato dall'asse x, dall'asse y e dal punto unità U si indica con
 (asse x, asse y, punto unità U).
(asse x, asse y, punto unità U).
Si vede che, dal riferimento formato dall'asse x, dall'asse y e dal punto unità U, i punti O, Ux, Uy sono distinti e non allineati.
Viceversa, si considerino tre punti distinti non allineati O, Ux, Uy; essi, in un riferimento del piano euclideo, rappresentano il punto origine, il punto unità dell'asse x ed il punto unità dell'asse y.
Se sul piano euclideo π si fissa un riferimento, si determina una bigezione:

Dimostrazione.
Si considerino le bigezioni fx ed fy, che associano rispettivamente ai punti Px e Py le ascisse x ed y rispetto ai riferimenti (O, Ux) ed
(O, Ux) ed  (O, Uy).
(O, Uy).
Si definisce f come applicazione di π in R R, tale che ad ogni punto P di π risulta che f(P) è uguale alla coppia (fx(Px), fy(Py)), cioè
R, tale che ad ogni punto P di π risulta che f(P) è uguale alla coppia (fx(Px), fy(Py)), cioè

Si dimostra che f è bigettiva, cioè è surgettiva ed ingettiva.
Infatti, si dimostra prima che f è surgettiva, cioè
 (x, y)
(x, y) R
R  R
R  P
P π
π  f(P) = (x, y).
f(P) = (x, y).
Allo scopo, si supponga di avere una coppia (x, y) R
R 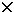 R ed i due punti
R ed i due punti
f-1x(X), f-1y(Y) e Px = f-1x(X), Py = f-1y(Y).
Ma, dai punti Px e Py così ottenuti, le parallele all'asse delle x ed a quello delle y danno il punto P, tale che
f(P) = (x, y),
come volevasi dimostrare.
Si dimostra ora che f è ingettiva, cioè
f(P) = f(P') P = P'.
P = P'.
f(P) = f(P') fx(Px) = fx(P'x), fy(Py) = fy(P'y)
fx(Px) = fx(P'x), fy(Py) = fy(P'y)  P = P',
P = P',
come volevasi dimostrare.
Si è quindi dimostrato che la bigezione f sopra definita associa ad ogni punto una coppia ordinata di numeri, coppia delle coordinate del punto P rispetto al riferimento.
Il primo elemento si chiama ascissa di P, il secondo si chiama ordinata di P.
Se P = 0, ascissa ed ordinata sono nulle.
Se P appartiene all'asse x, si ha P = Px, mentre Py = 0.
Se P appartiene all'asse y, si ha P = Py, mentre Px = 0.
In definitiva, tutti i punti dell'asse x hanno ordinata 0 e tutti i punti dell'asse y hanno ascissa 0, mentre al punto unità U è associata la coppia (1, 1).
Relazione fra le coordinate di un punto del piano rispetto a due riferimenti
Siano (O, Ux, Uy) ed
(O, Ux, Uy) ed  '(O', U'x, U'y) due riferimenti, e si indichino rispettivamente con f la bigezione di π in R2, che associa ad ogni punto P
'(O', U'x, U'y) due riferimenti, e si indichino rispettivamente con f la bigezione di π in R2, che associa ad ogni punto P π una coppia di coordinate (x, y)
π una coppia di coordinate (x, y) R2, e con f' la bigezione di π in R2, che associa ad ogni punto P
R2, e con f' la bigezione di π in R2, che associa ad ogni punto P π una coppia di coordinate (x', y')
π una coppia di coordinate (x', y') R2, cioè
R2, cioè

f ed f' si chiamano rispettivamente sistemi coordinati rispetto ad ed
ed  '.
'.
Si tratta di vedere le relazioni intercorrenti tra le coordinate dello stesso punto rispetto ai due riferimenti.
Allo scopo, si consideri l'inversa di f, cioè

Dunque, f' ο f-1è una bigezione, cioè una trasformazione di R2 in sé.
Si indica ora

pertanto T trasforma le coordinate di P nel riferimento in quelle di P nel riferimento
in quelle di P nel riferimento  '.
'.
Le relazioni tra x ed x', y ed y' sono le seguenti:

dove aij, con i = 1, 2, ... ; j = 1, 2, 3, ... sono numeri reali.
Si osserva ora che

cioè è la misura del segmento orientato rispetto ad (O', U'x), essendo
rispetto ad (O', U'x), essendo  ed
ed  le proiezioni sull'asse x' dei punti O ed Ux, condotte parallelamente all'asse y' congiungente O' con U'y.
le proiezioni sull'asse x' dei punti O ed Ux, condotte parallelamente all'asse y' congiungente O' con U'y.
Si osserva inoltre che

cioè è la misura del segmento orientato rispetto ad (O', U'x), essendo
rispetto ad (O', U'x), essendo  ed
ed  le proiezioni sull'asse x' dei punti O ed Uy, condotte parallelamente all'asse y' congiungente O' con U'y.
le proiezioni sull'asse x' dei punti O ed Uy, condotte parallelamente all'asse y' congiungente O' con U'y.
cioè è la misura del segmento orientato rispetto ad (O', U'y), essendo
rispetto ad (O', U'y), essendo  ed
ed  le proiezioni sull'asse y' dei punti O ed Uy, condotte parallelamente all'asse x' congiungente O' con U'x.
le proiezioni sull'asse y' dei punti O ed Uy, condotte parallelamente all'asse x' congiungente O' con U'x.
Ed infine
(a13, a23)
è la coppia di coordinate dell'origine nel nuovo riferimento.

Poichè T è una bigezione, il sistema suddetto ha il seguente determinante diverso da zero:

Una bigezione

si dice trasformazione affine di R2.
Si indica con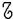 l'insieme delle trasformazioni affini di R2 e si dimostra che, se
l'insieme delle trasformazioni affini di R2 e si dimostra che, se  (O, Ux, Uy) è un riferimento su π, f è il sistema coordinato relativo ad
(O, Ux, Uy) è un riferimento su π, f è il sistema coordinato relativo ad  e T è una trasformazione affine di R2, allora f' è il sistema coordinato relativo ad
e T è una trasformazione affine di R2, allora f' è il sistema coordinato relativo ad  ', risulta f' ο f-1 = T, cioè:
', risulta f' ο f-1 = T, cioè:

Poichè si è visto che T pone una relazione tra le coordinate di un punto rispetto a due riferimenti,

si chiama sistema di equazioni della trasformazione rispetto ad ed
ed  '.
'.
Si considerino ora l'insieme C dei numeri complessi e la trasformazione

che si chiama trasformazione affine reale di C2.
Poichè si ha

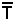 è una bigezione, poichè inoltre i coefficienti del sistema suddetto sono reali, si vede che
è una bigezione, poichè inoltre i coefficienti del sistema suddetto sono reali, si vede che 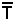 trasforma coppie reali in coppie reali.
trasforma coppie reali in coppie reali.
Infatti
 (x, y)
(x, y) R2 :
R2 : 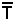 (x, y)
(x, y) R2,
R2,
ed essendo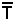 bigettiva, se (x, y)
bigettiva, se (x, y) C2,
C2,  (x, y) è complesso.
(x, y) è complesso.
Riferimento metrico
Si consideri il piano euclideo e la terna dei punti non allineati, soddisfacenti le seguenti condizioni:
OUx = OUy,
inoltre la coppia delle rette associate alle semirette OUx, OUy, dev'essere tale da formare un angolo di π/2.
Un tale riferimento prende il nome di riferimento metrico.

Riferimento polare
Si considerino nel piano euclideo una semiretta di origine O passante per il punto P ed il punto unità U. Sia φ l'angolo determinato dall'asse polare e dalla semiretta, tale che
0 ≤ φ < 2π.

Si prende ora ρ > 0, quindi al punto P resta associata la coppia (ρ, φ).
Viceversa, se è assegnata una coppia (ρ, φ), si può determinare un solo punto al quale è associata questa coppia.
Così operando, si dice che nel piano è stato fissato un riferimento polare, ρ prende il nome di raggio vettore e φ quello di anomalia.
In tal caso, non si ha alcuna bigezione del punto del piano, perchè al punto O, chiamato polo, non è associata alcuna coppia (ρ, φ).
Se si considera

è fissata una corrispondenza tra i punti del piano e le coppie (ρ, φ).
Raggio vettore
Il raggio vettore ρ è la misura del segmento OP secondo il segmento unitario OU.
Per l'anomalia φ si possono esprimere le seguenti limitazioni:
φ < 0, φ > 0,
se si considera l'origine 0 ≤ φ < 2π.
Si considerino nel piano euclideo un punto P, il segmento OP e l'angolo φ < π che l'asse polare forma con una delle due semirette. Si osservi che l'angolo considerato è quello minore di π perchè la retta è stata orientata in modo tale da avere ciò. Se si considera un punto Q, il segmento orientato ha il verso contrario a quello stabilito. Nel primo caso, il raggio vettore è positivo, nel secondo è negativo e quindi l'anomalia è definita a meno di multipli interi di 2π.

Relazione fra un riferimento metrico ed un riferimento polare
Si consideri un riferimento polare, cioè al piano euclideo si associa la coppia (ρ, φ), ρ ≠ 0, φ ≥ 0. Si consideri inoltre un riferimento metrico che abbia origine nel polo O, come asse delle x l'asse polare e come asse delle y la normale all'asse polare. Così operando, il riferimento metrico è stato associato al riferimento polare. Per trovare la relazione fra il riferimento metrico e quello polare, è necessario mettere in relazione le coordinate del punto P che nel riferimento metrico ha coordinate (x, y), mentre nel riferimento polare ha coordinate (ρ, φ).

Dalla figura suddetta, si ha:

Tali relazioni permettono di passare dal riferimento polare al riferimento metrico.
Viceversa, per passare dal riferimento metrico al riferimento polare, si trovano le relative relazioni, come segue:

Dunque, dalle coordinate metriche (x, y) del punto P, si è passati a quelle polari (ρ, φ), come volevasi.
Distanza di due punti in un riferimento polare

Applicando il teorema di Carnot al triangolo OPQ, si ha:
d2 = 2 = ρ12 + ρ22 - 2ρ1ρ2cos(φ2 - φ1) ≥ (ρ2 - ρ1)2.
2 = ρ12 + ρ22 - 2ρ1ρ2cos(φ2 - φ1) ≥ (ρ2 - ρ1)2.
Cambiamento di riferimento metrico nel piano
Si fissino nel piano due riferimenti metrici, Oxy ed O'x'y'.

Si osserva che gli assi x ed x', e rispettivamente y ed y', devono essere paralleli e concordi.
Si considerino ora un punto P(x, y) rispetto al riferimento Oxy, P(x', y') rispetto al riferimento O'x'y' e O'(a, b).
Dalla figura suddetta, hanno senso le seguenti condizioni:

Dunque, risulta

cioè

Quindi, si sono trovate le coordinate del punto P in un altro riferimento; tale riferimento è stato ottenuto mediante la trasformazione degli assi e le equazioni sono quelle ora scritte.
Altro tipo di cambiamento di riferimento
Si ricorda che:

Ciò osservato, si considerino i riferimenti metrici Oxy ed O'x'y', aventi entrambi la stessa origine in O, e si supponga che l'asse x' sia sfasato di un angolo φ rispetto ad x, cioè che sia

Si considera un punto P(x', y') rispetto ad Ox'y' e P(x, y) rispetto ad Oxy.
In forza della 1), si ha

In forza della 2), invece, si ha


Dopo di ciò, il diagramma fornisce le seguenti condizioni:

Si osserva ora che

Si ha quindi:

Ragionando in modo analogo, si ha:
y' = -senφ + ycosφ.
Dunque:
x' = xcosφ + ysenφ, y' = -senφ + ycosφ.
Si considerino i riferimenti metrici Oxy ed O'xy, aventi entrambi la stessa unità di misura; si vogliono determinare le equazioni in un nuovo riferimento.
Ovviamente risulta O(a, b), inoltre

Si considera un riferimento avente origine in O' e gli assi paralleli agli assi delle x e delle y nel riferimento Oxy, sia esso
Si ha:

Si considera ora il cambiamento riferimento che permette il passaggio da O'xy ad

Si ha:

Quindi, risulta
x' = (x - a)cosφ + (y - b)senφ,
y' = (x - a)senφ + (y - b)cosφ.
La terna formata dall'asse x, dall'asse y e dal punto U si chiama riferimento sul piano euclideo.

Si considerino ora le parallele per U all'asse x ed all'asse y, si ottengono pertanto due intersezioni, una sull'asse x, Ux, l'altra sull'asse y, Uy.
Ux ed Uy rappresentano i punti unità dell'asse x e dell'asse y.
Il punto di intersezione dell'asse x e dell'asse y si chiama origine e si indica con O.
Il riferimento formato dall'asse x, dall'asse y e dal punto unità U si indica con
Si vede che, dal riferimento formato dall'asse x, dall'asse y e dal punto unità U, i punti O, Ux, Uy sono distinti e non allineati.
Viceversa, si considerino tre punti distinti non allineati O, Ux, Uy; essi, in un riferimento del piano euclideo, rappresentano il punto origine, il punto unità dell'asse x ed il punto unità dell'asse y.
Se sul piano euclideo π si fissa un riferimento, si determina una bigezione:
Dimostrazione.
Si considerino le bigezioni fx ed fy, che associano rispettivamente ai punti Px e Py le ascisse x ed y rispetto ai riferimenti
Si definisce f come applicazione di π in R
Si dimostra che f è bigettiva, cioè è surgettiva ed ingettiva.
Infatti, si dimostra prima che f è surgettiva, cioè
Allo scopo, si supponga di avere una coppia (x, y)
f-1x(X), f-1y(Y) e Px = f-1x(X), Py = f-1y(Y).
Ma, dai punti Px e Py così ottenuti, le parallele all'asse delle x ed a quello delle y danno il punto P, tale che
f(P) = (x, y),
come volevasi dimostrare.
Si dimostra ora che f è ingettiva, cioè
f(P) = f(P')
f(P) = f(P')
come volevasi dimostrare.
Si è quindi dimostrato che la bigezione f sopra definita associa ad ogni punto una coppia ordinata di numeri, coppia delle coordinate del punto P rispetto al riferimento.
Il primo elemento si chiama ascissa di P, il secondo si chiama ordinata di P.
Se P = 0, ascissa ed ordinata sono nulle.
Se P appartiene all'asse x, si ha P = Px, mentre Py = 0.
Se P appartiene all'asse y, si ha P = Py, mentre Px = 0.
In definitiva, tutti i punti dell'asse x hanno ordinata 0 e tutti i punti dell'asse y hanno ascissa 0, mentre al punto unità U è associata la coppia (1, 1).
Relazione fra le coordinate di un punto del piano rispetto a due riferimenti
Siano

f ed f' si chiamano rispettivamente sistemi coordinati rispetto ad
Si tratta di vedere le relazioni intercorrenti tra le coordinate dello stesso punto rispetto ai due riferimenti.
Allo scopo, si consideri l'inversa di f, cioè
Dunque, f' ο f-1è una bigezione, cioè una trasformazione di R2 in sé.
Si indica ora
pertanto T trasforma le coordinate di P nel riferimento
Le relazioni tra x ed x', y ed y' sono le seguenti:

dove aij, con i = 1, 2, ... ; j = 1, 2, 3, ... sono numeri reali.
Si osserva ora che
cioè è la misura del segmento orientato
Si osserva inoltre che
cioè è la misura del segmento orientato
Si osserva ancora che

cioè è la misura del segmento orientato rispetto ad (O', U'y), essendo
rispetto ad (O', U'y), essendo  ed
ed  le proiezioni sull'asse y' dei punti O ed Ux, condotte parallelamente all'asse x' congiungente O' con U'x.
le proiezioni sull'asse y' dei punti O ed Ux, condotte parallelamente all'asse x' congiungente O' con U'x.
Inoltre è

cioè è la misura del segmento orientato
Inoltre è
cioè è la misura del segmento orientato
Ed infine
(a13, a23)
è la coppia di coordinate dell'origine nel nuovo riferimento.

Poichè T è una bigezione, il sistema suddetto ha il seguente determinante diverso da zero:

Una bigezione
si dice trasformazione affine di R2.
Si indica con

Poichè si è visto che T pone una relazione tra le coordinate di un punto rispetto a due riferimenti,

si chiama sistema di equazioni della trasformazione rispetto ad
Si considerino ora l'insieme C dei numeri complessi e la trasformazione
che si chiama trasformazione affine reale di C2.
Poichè si ha

Infatti
ed essendo
Riferimento metrico
Si consideri il piano euclideo e la terna dei punti non allineati, soddisfacenti le seguenti condizioni:
OUx = OUy,
inoltre la coppia delle rette associate alle semirette OUx, OUy, dev'essere tale da formare un angolo di π/2.
Un tale riferimento prende il nome di riferimento metrico.

Riferimento polare
Si considerino nel piano euclideo una semiretta di origine O passante per il punto P ed il punto unità U. Sia φ l'angolo determinato dall'asse polare e dalla semiretta, tale che
0 ≤ φ < 2π.

Si prende ora ρ > 0, quindi al punto P resta associata la coppia (ρ, φ).
Viceversa, se è assegnata una coppia (ρ, φ), si può determinare un solo punto al quale è associata questa coppia.
Così operando, si dice che nel piano è stato fissato un riferimento polare, ρ prende il nome di raggio vettore e φ quello di anomalia.
In tal caso, non si ha alcuna bigezione del punto del piano, perchè al punto O, chiamato polo, non è associata alcuna coppia (ρ, φ).
Se si considera
è fissata una corrispondenza tra i punti del piano e le coppie (ρ, φ).
Raggio vettore
Il raggio vettore ρ è la misura del segmento OP secondo il segmento unitario OU.
Per l'anomalia φ si possono esprimere le seguenti limitazioni:
φ < 0, φ > 0,
se si considera l'origine 0 ≤ φ < 2π.
Si considerino nel piano euclideo un punto P, il segmento OP e l'angolo φ < π che l'asse polare forma con una delle due semirette. Si osservi che l'angolo considerato è quello minore di π perchè la retta è stata orientata in modo tale da avere ciò. Se si considera un punto Q, il segmento orientato ha il verso contrario a quello stabilito. Nel primo caso, il raggio vettore è positivo, nel secondo è negativo e quindi l'anomalia è definita a meno di multipli interi di 2π.

Relazione fra un riferimento metrico ed un riferimento polare
Si consideri un riferimento polare, cioè al piano euclideo si associa la coppia (ρ, φ), ρ ≠ 0, φ ≥ 0. Si consideri inoltre un riferimento metrico che abbia origine nel polo O, come asse delle x l'asse polare e come asse delle y la normale all'asse polare. Così operando, il riferimento metrico è stato associato al riferimento polare. Per trovare la relazione fra il riferimento metrico e quello polare, è necessario mettere in relazione le coordinate del punto P che nel riferimento metrico ha coordinate (x, y), mentre nel riferimento polare ha coordinate (ρ, φ).

Dalla figura suddetta, si ha:

Tali relazioni permettono di passare dal riferimento polare al riferimento metrico.
Viceversa, per passare dal riferimento metrico al riferimento polare, si trovano le relative relazioni, come segue:

Dunque, dalle coordinate metriche (x, y) del punto P, si è passati a quelle polari (ρ, φ), come volevasi.
Distanza di due punti in un riferimento polare
Siano assegnati in un riferimento polare due punti P(ρ1, φ1), Q(ρ2, φ2).

Applicando il teorema di Carnot al triangolo OPQ, si ha:
d2 =
Cambiamento di riferimento metrico nel piano
Si fissino nel piano due riferimenti metrici, Oxy ed O'x'y'.

Si osserva che gli assi x ed x', e rispettivamente y ed y', devono essere paralleli e concordi.
Si considerino ora un punto P(x, y) rispetto al riferimento Oxy, P(x', y') rispetto al riferimento O'x'y' e O'(a, b).
Dalla figura suddetta, hanno senso le seguenti condizioni:

Dunque, risulta

cioè

Quindi, si sono trovate le coordinate del punto P in un altro riferimento; tale riferimento è stato ottenuto mediante la trasformazione degli assi e le equazioni sono quelle ora scritte.
Altro tipo di cambiamento di riferimento
Si ricorda che:

Ciò osservato, si considerino i riferimenti metrici Oxy ed O'x'y', aventi entrambi la stessa origine in O, e si supponga che l'asse x' sia sfasato di un angolo φ rispetto ad x, cioè che sia
Si considera un punto P(x', y') rispetto ad Ox'y' e P(x, y) rispetto ad Oxy.
In forza della 1), si ha

In forza della 2), invece, si ha


Dopo di ciò, il diagramma fornisce le seguenti condizioni:
Si osserva ora che
Si ha quindi:

Ragionando in modo analogo, si ha:
y' = -senφ + ycosφ.
Dunque:
x' = xcosφ + ysenφ, y' = -senφ + ycosφ.
Si considerino i riferimenti metrici Oxy ed O'xy, aventi entrambi la stessa unità di misura; si vogliono determinare le equazioni in un nuovo riferimento.
Ovviamente risulta O(a, b), inoltre
Si considera un riferimento avente origine in O' e gli assi paralleli agli assi delle x e delle y nel riferimento Oxy, sia esso
Si ha:
Si considera ora il cambiamento riferimento che permette il passaggio da O'xy ad

Si ha:

Quindi, risulta
x' = (x - a)cosφ + (y - b)senφ,
y' = (x - a)senφ + (y - b)cosφ.