SISTEMI COORDINATI ---> INDICE
Si
fissi un riferimento  (O, U)
sulla retta euclidea r e si consideri l'applicazione f che, ad ogni
punto della retta, associa un numero reale; tale applicazione è una
bigezione dei punti della retta r nell'insieme dei numeri reali R, cioè:
(O, U)
sulla retta euclidea r e si consideri l'applicazione f che, ad ogni
punto della retta, associa un numero reale; tale applicazione è una
bigezione dei punti della retta r nell'insieme dei numeri reali R, cioè:
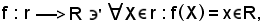
dove x è l'ascissa di X rispetto ad (O, U).
(O, U).
Tale applicazione f si chiama sistema coordinato relativo ad (O, U).
(O, U).
Si esprimono ora, mediante prodotto di applicazioni, le relazioni esistenti fra sistemi coordinati relativi a due riferimenti diversi. Si consideri quindi un altro riferimento (O', U') sulla retta euclidea r e si consideri l'applicazione f' che, ad ogni
punto della retta, associa un numero reale; tale applicazione è anche una
bigezione dei punti della retta r nell'insieme dei numeri reali R, cioè:
(O', U') sulla retta euclidea r e si consideri l'applicazione f' che, ad ogni
punto della retta, associa un numero reale; tale applicazione è anche una
bigezione dei punti della retta r nell'insieme dei numeri reali R, cioè:
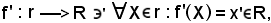
dove x' è l'ascissa di X rispetto ad (O', U').
(O', U').
Si ricorda ora che, rispetto ai riferimenti (O, U) ed
(O, U) ed  (O', U'), è stata definita la trasformazione lineare intera che è una bigezione dell'insieme dei numeri reali su se stesso,
(O', U'), è stata definita la trasformazione lineare intera che è una bigezione dell'insieme dei numeri reali su se stesso,

tale che ad ogni x R corrisponde x' = αx + β, dove
R corrisponde x' = αx + β, dove
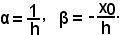
Si indichi con T tale trasformazione e sia T(x) = αx + β, o anche
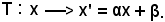
T(x) rappresenta la trasformazione lineare intera definita dai due riferimenti (O, U) ed
(O, U) ed  (O', U'), mentre f ed f' i sistemi coordinati relativi rispettivamente ad
(O', U'), mentre f ed f' i sistemi coordinati relativi rispettivamente ad  (O, U) ed
(O, U) ed  (O', U').
(O', U').
In tali condizioni, esiste la relazione
f' = Tf,
cioè f' è uguale al prodotto operativo di due applicazioni, ed in tal modo ad ogni ascissa del riferimento OU viene associata l'ascissa del riferimento O'U'. In altri termini f' è tale che, ad ogni punto X della retta r, fa corrispondere un numero reale x mediante la f ed al numero reale x fa corrispondere il numero reale x' mediante la trasformazione lineare T.
Da ciò segue che
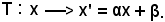 Pertanto
Pertanto
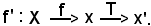
Si dimostra ora che
f' = T ο f.
Allo scopo si consideri un punto X della retta r, allora
f'(X) = x',
ed essendo
x' = αx + β
il valore della trasformazione lineare in x, si ha
f'(X) = x' = αx + β = T(x) = T(f(X)) = T ο f(X),
come volevasi dimostrare. Si è quindi dimostrato che, dato un riferimento  (O, U) ed una trasformazione lineare
(O, U) ed una trasformazione lineare
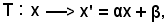
esiste un unico riferimento che permette il passaggio dalle precedenti alle nuove ascisse.
Se (O, U) è un riferimento, f un sistema coordinato e T una trasformazione lineare, la bigezione
(O, U) è un riferimento, f un sistema coordinato e T una trasformazione lineare, la bigezione
f' = Tf,
che fa corrispondere a punti della retta numeri reali, è il sistema coordinato relativo ad un determinato riferimento, cioè Tf è un sistema coordinato di un altro riferimento (O', U').
(O', U').
dove x è l'ascissa di X rispetto ad
Tale applicazione f si chiama sistema coordinato relativo ad
Si esprimono ora, mediante prodotto di applicazioni, le relazioni esistenti fra sistemi coordinati relativi a due riferimenti diversi. Si consideri quindi un altro riferimento
dove x' è l'ascissa di X rispetto ad
Si ricorda ora che, rispetto ai riferimenti
tale che ad ogni x
Si indichi con T tale trasformazione e sia T(x) = αx + β, o anche
T(x) rappresenta la trasformazione lineare intera definita dai due riferimenti
In tali condizioni, esiste la relazione
f' = Tf,
cioè f' è uguale al prodotto operativo di due applicazioni, ed in tal modo ad ogni ascissa del riferimento OU viene associata l'ascissa del riferimento O'U'. In altri termini f' è tale che, ad ogni punto X della retta r, fa corrispondere un numero reale x mediante la f ed al numero reale x fa corrispondere il numero reale x' mediante la trasformazione lineare T.
Da ciò segue che
Si dimostra ora che
f' = T ο f.
Allo scopo si consideri un punto X della retta r, allora
f'(X) = x',
ed essendo
x' = αx + β
il valore della trasformazione lineare in x, si ha
f'(X) = x' = αx + β = T(x) = T(f(X)) = T ο f(X),
come volevasi dimostrare.
esiste un unico riferimento che permette il passaggio dalle precedenti alle nuove ascisse.
Se
f' = Tf,
che fa corrispondere a punti della retta numeri reali, è il sistema coordinato relativo ad un determinato riferimento, cioè Tf è un sistema coordinato di un altro riferimento