MIKY & GENNY
CIRCONFERENZA E COMPLEMENTI ---> INDICE
Dalla geometria elementare è noto che:
-la circonferenza è il luogo geometrico dei punti del piano che distano da un punto detto centro, di una distanza data detta raggio.
Mentre nella geometria elementare la linea così definita si chiama "circonferenza", e la superficie racchiusa da tale linea "cerchio", in geometria analitica con la parola "cerchio" si indicherà sempre e soltanto la linea.
Brevemente, in geometria analitica è indifferente dire circonferenza o cerchio.
Si ricava ora l'equazione della circonferenza dalla sua definizione geometrica.
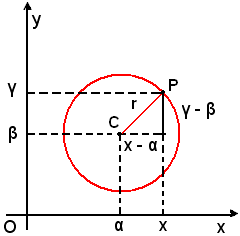
Sia C(α, β) il centro della circonferenza ed r il suo raggio; se P di coordinate x ed y è un suo punto, risulta:
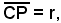
ossia, applicando la formula della distanza del punto C dal punto P, si ha
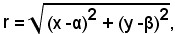
da cui, elevando al quadrato ambo i membri, si ottiene
Sviluppando e ordinando la (1) diventa:
(2) x2 + y2 - 2αx - 2 βy + γ = 0,
ove si è posto:
γ = α2 + β2 - r2.
La (2) è soddisfatta dalle coordinate di tutti i punti della circonferenza; viceversa, se le coordinate di un punto del piano soddisfano la (2), il punto ha distanza r dal centro, e perciò appartiene al cerchio. Si può dunque dire che l'equazione (2) rappresenta l'equazione del cerchio di centro C(α, β) e di raggio r.
Esempio
Determinare l'equazione del cerchio di centro (1, 2) e raggio 3.
Applicando la (1), si ha:
32 = (x - 1)2 + (y - 2)2
e sviluppando e riducendo, risulta
Esaminando la (2), si rileva quanto segue.
1)-Essa è un'equazione di secondo grado nelle variabili x e y.
La più generale equazione di secondo grado nelle variabili x e y è del tipo:
mx2 + nxy + py2 + rx + sy + t = 0.
Tale equazione rappresenta una circonferenza solo quando n = 0 e m = n.
In tal caso diventa:
mx2 + my2 + rx + sy + t = 0
e, dividendo per m≠0, si ha
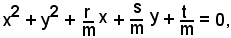
posto
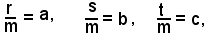
risulta
x2 + y2 + ax + by + c = 0.
2)-Il coefficiente di x2 è uguale al coefficiente di y2 e può ridursi uguale all'unità, dividendo l'equazione per tale coefficiente supposto diverso da zero.
Se i coefficienti di x2 ed y2 sono uguali all'unità, l'equazione della circonferenza si dice normale.
3)-L'equazione manca del termine rettangolare in xy.
4)-I coefficienti α, β, γ sono tali che:
α2 + β2 - γ = r2 > 0.
Viceversa, qualsiasi equazione del tipo:
(3) x2 + y2 + ax + by + c = 0,
cioè "qualsiasi equazione di secondo grado nelle variabili x e y, avente i coefficiente di x2 e di y2 uguali fra loro, in particolare uguali all'unità, e priva del termine xy rappresenta una circonferenza".
Infatti, la (3) si può scrivere:

Si passa dalla (3) alla (4) aggiungendo ad entrambi i membri della (3) la quantità
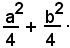
Il primo membro della (4) rappresenta il quadrato della distanza fra il punto variabile (x, y) ed il punto fisso
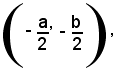
mentre il secondo membro è costante.
Si conclude che la (3) e la (4) rappresentano il luogo geometrico dei punti del piano equidistanti dal punto fisso
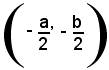
di una distanza data
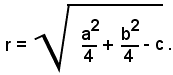
In altri termini, la (3) e la (4) rappresentano il cerchio di centro
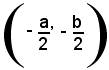
e raggio
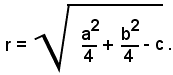
Se

r è reale e si ha la circonferenza propriamente detta.
Se
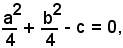
r = 0 ed il cerchio si riduce nel campo reale ad un punto, cioè al suo centro, cerchio di raggio nullo.
Se
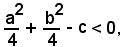
si ha un cerchio immaginario.
Da quanto detto, si può concludere che:
-data una circonferenza, le coordinate del centro sono date dai semicoefficienti dei termini di primo grado cambiati di segno e il raggio è uguale alla radice quadrata della somma dei quadrati delle coordinate del centro diminuita del termine noto.
Esempi
1)-Trovare il centro ed il raggio del cerchio di equazione:
x2 + y2 - 4x + 8y - 5 = 0.
Tale equazione rappresenta effettivamente la circonferenza, perchè è di secondo grado in x ed y, ha i coefficienti di x2 e y2 uguali fra loro e manca del termine xy.
Le coordinate del centro sono date dai semicoefficienti, cambiati di segno, dei termini di primo grado dell'equazione, cioè esse sono: (2, - 4).
Il raggio è uguale alla radice quadrata della somma dei quadrati delle coordinate del centro meno il termine noto dell'equazione, cioè:
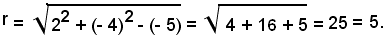
Dunque, la circonferenza di equazione x2 + y2 - 4x + 8y - 5 = 0 ha centro C(2, -4) e r = 5.
2)-Verificare se l'equazione:
5x2 + y2 - x - y - 1 = 0.
rappresenta una circonferenza.
L'equazione suddetta non rappresenta una circonferenza perchè il coefficiente di x2 non è uguale al coefficiente di y2.
3)-Trovare il centro ed il raggio della circonferenza di equazione:
4x2 + 4y2 - 2x - 4y + 1 = 0.
L'equazione rappresenta una circonferenza, in quanto è un'equazione di secondo grado nelle variabili x ed y, il coefficiente di x2 è uguale al coefficiente di y2 e manca del termine rettangolare xy.
Si riduce l'equazione della circonferenza a forma normale, dividendo l'equazione per 4, coefficiente di x2 e di y2, si ottiene:
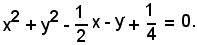
Procedendo come nell'esempio precedente, le coordinate del centro e il raggio sono:
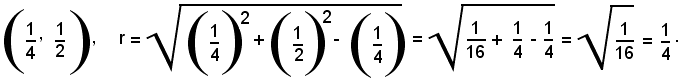
Le coordinate del centro e il centro della circonferenza si possono determinare anche con il metodo del completamento dei quadrati, cioè si cerca di porre l'equazione della circonferenza sotto la forma (2).
Con un artificio, si cerca di ottenere al primo membro dell'equazione la somma di due quadrati perfetti.
L'espressione:
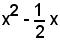
si può considerare come somma del quadrato di x più il doppio prodotto di x per
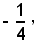
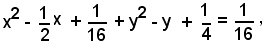
ossia
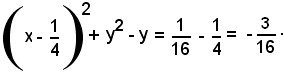
Analogamente l'espressione:
y2 - y
si può scrivere:
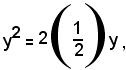
che differisce da un quadrato perfetto per la mancanza del termine
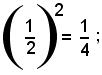
aggiungendo ad ambo i membri tale termine, si ha:
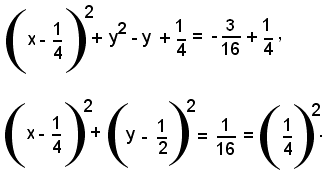
Confrontando questa equazione con la (2), si trova:
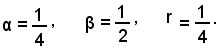
Circonferenze in posizione particolare
1)-Quando nell'equazione di una circonferenza manca il termine in x, la circonferenza ha il centro sull'asse y.
Esempio
L'equazione.
x2 + y2 - 4y + 3 = 0.
rappresenta una circonferenza avente il centro nel punto C(0, 2) e
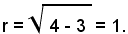
2)-Quando nell'equazione di una circonferenza manca il termine in y, la circonferenza ha il centro sull'asse x.
Esempio
L'equazione
x2 + y2 - 6x + 8 = 0.
rappresenta una circonferenza avente il centro nel punto C(3, 0) e
3)-Quando nell'equazione di una circonferenza mancano i termini in x ed in y, la circonferenza ha il centro nell'origine degli assi.
Esempio
L'equazione
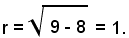
x2 + y2 - 9 = 0.
rappresenta una circonferenza avente di centro O(0, 0) e raggio r = 3.
Dunque, l'equazione della circonferenza avente per centro l'origine O e per raggio r è del tipo:
x2 + y2 = r2.
4)-Quando nell'equazione di una circonferenza mancano il termine noto, la circonferenza passa per l'origine.
Esempio
L'equazione
x2 + y2 - 6x - 8y = 0.
rappresenta una circonferenza passante per l'origine O(0, 0).
Infatti, le coordinate (0, 0) dell'origine soddisfano l'equazione data, cioè sostituendo nell'equazione data al posto della x e della y le coordinate (0, 0) dell'origine, si ha un'identità:
02 + 02 - 6· 0 - 8· 0 = 0.
Circonferenza sottoposta a determinate condizioni
L'equazione
x2 + y2 - 2αx - 2βy + γ = 0
della circonferenza di centro C(α, β) e raggio r dipende da tre coefficienti essenziali α, β, γ, a ciascuno dei quali si possono assegnare infiniti valori.
Per individuare una circonferenza, occorre quindi assegnare tre condizioni indipendenti.
Se si sottopone una circonferenza a tre condizioni indipendenti, queste si traducono in un sistema di tre equazioni nelle incognite α, β, γ che a seconda del grado determina uno o più cerchi.
Si esaminano ora le condizioni a cui può essere sottoposto un cerchio e si ricerca il loro grado.
a)-Condizione di passaggio di un cerchio per un punto, o di appartenenza di un punto ad un cerchio
Infatti, affinchè il punto P(x0, y0) appartenga al cerchio di equazione
x2 + y2 - 2αx - 2βy + γ = 0,
occorre che le sue coordinate rappresentino una soluzione dell'equazione del cerchio, cioè si verifichi:
x02 + y02 - 2αx0 - 2βy0 + γ = 0,
che è un'equazione di primo grado nelle incognite α, β, γ.
Nota bene
Si deve ricordare che l'equazione x2 + y2 - 2αx - 2βy + γ = 0 ammette infinite soluzioni ottenute assegnando ad una delle incognite, x o y, valori arbitrari e determinando poi, dopo aver sostituito nell'equazione tale valore arbitrario, l'altra incognita. Ogni soluzione dell'equazione rappresenta un punto della circonferenza.
Esempio - Circonferenza per tre punti
Determinare l'equazione della circonferenza passante per i punti A(2, 1), B(1, 0), C(-1,2), non allineati.
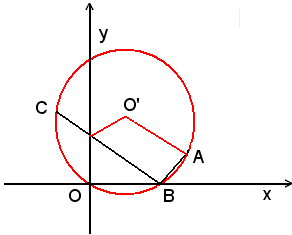
Per quanto detto in precedenza, il problema ammette una ed una sola soluzione, in quanto sono assegnate tre condizioni lineari indipendenti. Le tre condizioni si traducono in un sistema di primo grado di tre equazioni in tre incognite. Allo scopo, sia
x2 + y2 - 2αx - 2βy + γ = 0
l'equazione di una circonferenza generica.
I punti A, B, C appartengono alla circonferenza, se e solo se le loro coordinate soddisfano l'equazione della circonferenza.
Sostituendo successivamente nell'equazione al posto della x e della y le coordinate di A, B e C si ottengono tre equazioni nelle incognite α, β, γ:
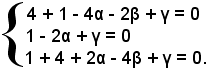
cioè
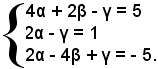
Per risolvere il sistema, conviene sommare la 2^ con la 3^ e la 1^ con la 3^ e determinare i valori di α e β che, sostituiti in una delle tre equazioni, danno i valori:
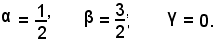
L'equazione cercata è:
x2 + y2 - x - 3y = 0.
Altro procedimento: il centro del cerchio richiesto dev'essere equidistante dai punti A, B, C; esso perciò si trova nel punto d'intersezione dell'asse del segmento AB con l'asse del segmento BC. L'asse del segmento AB ha equazione:

Elevando ambo i membri al quadrato e semplificando risulta:
x + y -2 = 0.
L'asse del segmento BC ha equazione:
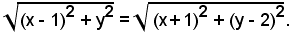
Elevando ambo i membri al quadrato e semplificando risulta:
x - y + 1 = 0.
Si risolve ora il sistema:
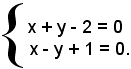
Le coordinate del centro del cerchio risultano:
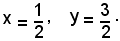
Noto

il raggio è dato dalla distanza di O' da uno dei tre punti dati:
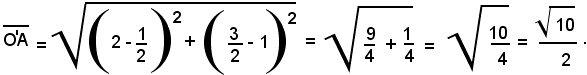
b)-Imporre ad un cerchio di avere un dato centro, equivale a dare due condizioni lineari, in quanto sono dati l'ascissa e l'ordinata del centro.
Esempio - Circonferenza di dato centro passante per un punto
Scrivere l'equazione di una circonferenza di centro C(3, 2) passante per il punto P(1, 2/3).
Il problema ammette una ed una sola soluzione, in quanto sono date tre condizioni lineari: due con l'ascissa e l'ordinata del centro e la terza con il passaggio per il punto P.
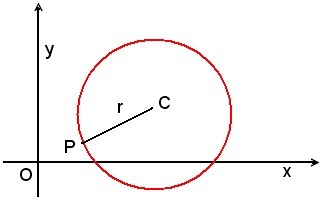
L'equazione della circonferenza si determina rapidamente sapendo che il raggio è dato dalla distanza di C da P, cioè:
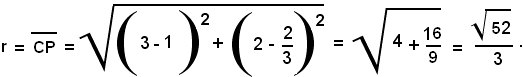
Applicando la (1), il cerchio richiesto di centro C e raggio r ha equazione:
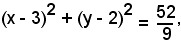
sviluppando e riducendo, si ha:
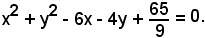
c)-Imporre ad un cerchio di avere un dato raggio equivale ad assegnare una condizione di secondo grado.
Infatti, r2 = α2 + β2 - γ rappresenta un'equazione di secondo grado nelle incognite α, β, γ.
Esempio - Circonferenze di dato raggio passanti per due punti.
Scrivere le equazioni dei cerchi aventi raggio r = 3 passanti per i punti A(1, 3), B(4, 0).
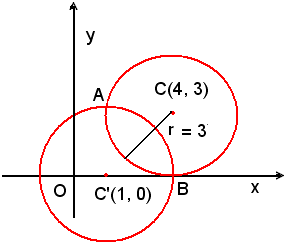
Il problema ammette due soluzioni, in quanto delle tre condizioni date, due sono di primo grado, cioè il passaggio del cerchio per i punti A e B, l'altra di secondo grado è data dal raggio al quadrato; si hanno dunque due cerchi.
Sia data l'equazione di un cerchio generico:
x2 + y2 - 2αx - 2 βy + γ = 0,
affinchè esso passi per i punti A e B, occorre che le coordinate di tali punti soddisfino l'equazione del cerchio. Sostituendo nell'equazione alla x e alla y le coordinate di A e B, si hanno le prime due equazioni nelle incognite α, β, γ, cioè:
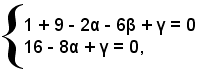
ossia
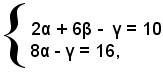
Il raggio del cerchio dev'essere uguale a 3; essendo r2 = α2 + β2 - γ, si ha la terza equazione
Quindi il sistema di secondo grado da risolvere è:
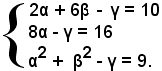
Per risolvere il sistema, si ricava α dalla prima x2 + y2 - x - 3y = 0 e si sostituisce il valore nelle altre due; si ricava β dalla seconda e si sostituisce il valore nelle altre due; infine si risolve l'equazione di secondo grado nell'incognita γ, ottenendo, dopo facili calcoli:
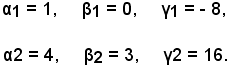
Le equazioni dei cerchi sono:
x2 + y2 - 2x - 8 = 0.
x2 + y2 - 8x - 6y + 16 = 0.
d)-Imporre ad un cerchio di essere tangente ad una retta in un punto assegnato equivale ad assegnare due condizioni lineari.
La prima condizione è che il cerchio passi per quel punto, la seconda p che il centro del cerchio si trovi sopra la normale per quel punto alla retta data.
Infatti, r2 = α2 + β2 - γ rappresenta un'equazione di secondo grado nelle incognite α, β, γ.
Esempio - Circonferenza tangente ad una retta in un punto dato e passante per quel punto.
Scrivere l'equazione della circonferenza tangente alla retta y + 1 = 0 nel punto A(0, -1) e passante per B(0, 3).
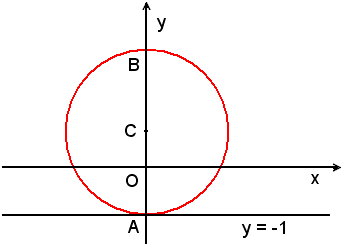
Il problema ammette una sola soluzione, in quanto sono date tre condizioni lineari. La prima che il cerchio passi per il punto A(0, -1); la seconda che il cerchio si trovi sulla perpendicolare alla retta y = -1 passante per A, cioè all'asse y e la terza il passaggio del cerchio per il punto B (0, 3).
Sia data l'equazione di un cerchio generico:
x2 + y2 - 2αx - 2βy + γ = 0.
Esso passa per il punto A(0, -1), se le coordinate del punto soddisfano l'equazione, cioè se si verifica:
1 + 2β + γ = 0.
Il cerchio è tangente alla retta y = -1 nel punto A(0, -1), se il centro si trova sulla perpendicolare per A alla retta y = -1.
Tale perpendicolare è l'asse y di equazione x = 0, cioè deve verificarsi α= 0.
Il cerchio passa per il punto B(0, 3) se:
9 - 6β + γ = 0.
Si risolve ora il sistema formato dalle tre relazioni:
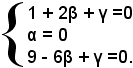
Si hanno i valori
α = 0, β = 1, γ = -3.
L'equazione del cerchio richiesto è:
x2 + y2 - 2y - 3 = 0.
Richiami
E' noto dalla geometria elementare che:
-una retta ha al massimo due punti in comune con una circonferenza, per questo si dice che la circonferenza è una curva del secondo ordine.
In generale si definisce ordine di una curva il numero delle intersezioni che la curva ha con una retta generica del piano.
-Le curve del primo ordine, rappresentate da equazioni di primo grado, si chiamano rette.
-Le curve del secondo ordine, rappresentate da equazioni di secondo grado nelle variabili x ed y si chiamano coniche.
-Le curve del terzo ordine, rappresentate da equazioni di terzo grado si chiamano cubiche.
-Le curve del quarto ordine, rappresentate da equazioni di quarto grado si chiamano quartiche, ecc.
Intersezioni di una retta con una circonferenza
Sia x2 + y2 - 2αx - 2βy + γ = 0 la circonferenza di centro C(α, β) e raggio r, y = mx + q una retta data, si vogliono determinare i punti comuni al cerchio e alla retta.
Le coordinate dei punti di intersezione del cerchio con la retta devono soddisfare l'equazione della retta, poichè tutti i punti stanno sulla retta; esse sono perciò le soluzioni del sistema formato dalle due equazioni:
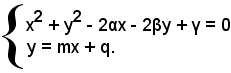
Se tale sistema ammette:
-due soluzioni reali e distinte, la retta ha due punti reali e distinti comuni con il cerchio, retta secante,
-se ha una soluzione, cioè due soluzioni reali e coincidenti, la retta ha un punto, cioè due punti coicidenti, in comune con il cerchio, retta tangente,
-se non ha soluzioni reali, la retta non ha punti comuni con il cerchio, retta esterna.
Esempi
1)-Determinare le intersezioni della retta x + 2y - 4 = 0 con la circonferenza di equazione:
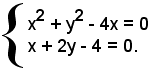
Sostituendo nella prima equazione il valore
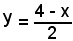
ricavato dalla seconda, si ha:
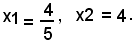
Le soluzioni del sistema sono:
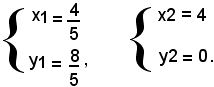
I punti
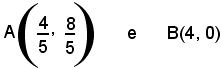
sono punti comuni al cerchio e alla retta.
La retta x + 2y - 4 = 0 è secante il cerchio x2 + y2 - 4x = 0.
Infatti, la distanza dal centro C(2, 0) del cerchio dalla retta è:
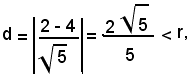
essendo
2)-Determinare le intersezioni della retta x - 3y + 2 = 0 con la circonferenza di equazione:
x2 + y2 - 4x + 4y - 2 = 0.
Si osservi che la retta è tangente alla circonferenza in quanto la distanza del centro C(2, -2) della circonferenza dalla retta è uguale al raggio.
Si ricordi che se una retta è rispettivamente secante, tangente, esterna ad un cerchio, la sua distanza dal centro del cerchio è rispettivamente minore, uguale o maggiore del raggio.
Infatti, si ha:
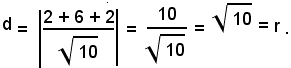
Per determinare le coordinate del punto di contatto o di tangenza della retta con la circonferenza si risolve il sistema formato dalle due equazioni:
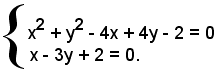
Sostituendo nella prima equazione il valore di x = 3y - 2, ricavato dalla seconda, si ha y1 = y2 = 1.
Le soluzioni del sistema sono:
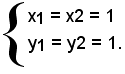
-la circonferenza è il luogo geometrico dei punti del piano che distano da un punto detto centro, di una distanza data detta raggio.
Mentre nella geometria elementare la linea così definita si chiama "circonferenza", e la superficie racchiusa da tale linea "cerchio", in geometria analitica con la parola "cerchio" si indicherà sempre e soltanto la linea.
Brevemente, in geometria analitica è indifferente dire circonferenza o cerchio.
Si ricava ora l'equazione della circonferenza dalla sua definizione geometrica.
Sia C(α, β) il centro della circonferenza ed r il suo raggio; se P di coordinate x ed y è un suo punto, risulta:
ossia, applicando la formula della distanza del punto C dal punto P, si ha
da cui, elevando al quadrato ambo i membri, si ottiene
(1) (x - α)2 + (y - β)2 = r2.

Sviluppando e ordinando la (1) diventa:
ove si è posto:
γ = α2 + β2 - r2.
La (2) è soddisfatta dalle coordinate di tutti i punti della circonferenza; viceversa, se le coordinate di un punto del piano soddisfano la (2), il punto ha distanza r dal centro, e perciò appartiene al cerchio. Si può dunque dire che l'equazione (2) rappresenta l'equazione del cerchio di centro C(α, β) e di raggio r.
Esempio
Determinare l'equazione del cerchio di centro (1, 2) e raggio 3.
Applicando la (1), si ha:
32 = (x - 1)2 + (y - 2)2
e sviluppando e riducendo, risulta
x2 + y2 - 2x - 4y - 4 = 0,
Esaminando la (2), si rileva quanto segue.
1)-Essa è un'equazione di secondo grado nelle variabili x e y.
La più generale equazione di secondo grado nelle variabili x e y è del tipo:
mx2 + nxy + py2 + rx + sy + t = 0.
Tale equazione rappresenta una circonferenza solo quando n = 0 e m = n.
In tal caso diventa:
mx2 + my2 + rx + sy + t = 0
e, dividendo per m≠0, si ha
posto
risulta
x2 + y2 + ax + by + c = 0.
2)-Il coefficiente di x2 è uguale al coefficiente di y2 e può ridursi uguale all'unità, dividendo l'equazione per tale coefficiente supposto diverso da zero.
Se i coefficienti di x2 ed y2 sono uguali all'unità, l'equazione della circonferenza si dice normale.
3)-L'equazione manca del termine rettangolare in xy.
4)-I coefficienti α, β, γ sono tali che:
α2 + β2 - γ = r2 > 0.
Viceversa, qualsiasi equazione del tipo:
(3) x2 + y2 + ax + by + c = 0,
cioè "qualsiasi equazione di secondo grado nelle variabili x e y, avente i coefficiente di x2 e di y2 uguali fra loro, in particolare uguali all'unità, e priva del termine xy rappresenta una circonferenza".
Infatti, la (3) si può scrivere:

Si passa dalla (3) alla (4) aggiungendo ad entrambi i membri della (3) la quantità
Il primo membro della (4) rappresenta il quadrato della distanza fra il punto variabile (x, y) ed il punto fisso
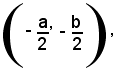
mentre il secondo membro è costante.
Si conclude che la (3) e la (4) rappresentano il luogo geometrico dei punti del piano equidistanti dal punto fisso
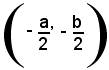
di una distanza data
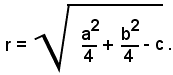
In altri termini, la (3) e la (4) rappresentano il cerchio di centro
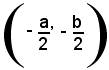
e raggio
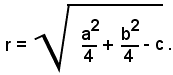
Se
r è reale e si ha la circonferenza propriamente detta.
Se
r = 0 ed il cerchio si riduce nel campo reale ad un punto, cioè al suo centro, cerchio di raggio nullo.
Se
si ha un cerchio immaginario.
Da quanto detto, si può concludere che:
-data una circonferenza, le coordinate del centro sono date dai semicoefficienti dei termini di primo grado cambiati di segno e il raggio è uguale alla radice quadrata della somma dei quadrati delle coordinate del centro diminuita del termine noto.
Esempi
1)-Trovare il centro ed il raggio del cerchio di equazione:
x2 + y2 - 4x + 8y - 5 = 0.
Tale equazione rappresenta effettivamente la circonferenza, perchè è di secondo grado in x ed y, ha i coefficienti di x2 e y2 uguali fra loro e manca del termine xy.
Le coordinate del centro sono date dai semicoefficienti, cambiati di segno, dei termini di primo grado dell'equazione, cioè esse sono: (2, - 4).
Il raggio è uguale alla radice quadrata della somma dei quadrati delle coordinate del centro meno il termine noto dell'equazione, cioè:
Dunque, la circonferenza di equazione x2 + y2 - 4x + 8y - 5 = 0 ha centro C(2, -4) e r = 5.
2)-Verificare se l'equazione:
5x2 + y2 - x - y - 1 = 0.
rappresenta una circonferenza.
L'equazione suddetta non rappresenta una circonferenza perchè il coefficiente di x2 non è uguale al coefficiente di y2.
3)-Trovare il centro ed il raggio della circonferenza di equazione:
4x2 + 4y2 - 2x - 4y + 1 = 0.
L'equazione rappresenta una circonferenza, in quanto è un'equazione di secondo grado nelle variabili x ed y, il coefficiente di x2 è uguale al coefficiente di y2 e manca del termine rettangolare xy.
Si riduce l'equazione della circonferenza a forma normale, dividendo l'equazione per 4, coefficiente di x2 e di y2, si ottiene:
Procedendo come nell'esempio precedente, le coordinate del centro e il raggio sono:
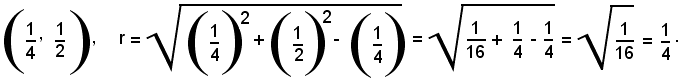
Le coordinate del centro e il centro della circonferenza si possono determinare anche con il metodo del completamento dei quadrati, cioè si cerca di porre l'equazione della circonferenza sotto la forma (2).
Con un artificio, si cerca di ottenere al primo membro dell'equazione la somma di due quadrati perfetti.
L'espressione:
si può considerare come somma del quadrato di x più il doppio prodotto di x per
cioè
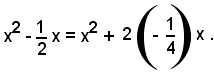
Questa differisce da un quadrato perfetto per la mancanza del termine
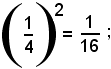
aggiungendo ad ambo i membri tale termine, si ha:
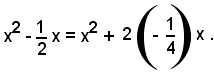
Questa differisce da un quadrato perfetto per la mancanza del termine
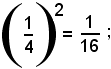
aggiungendo ad ambo i membri tale termine, si ha:
ossia
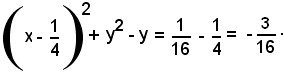
Analogamente l'espressione:
y2 - y
si può scrivere:
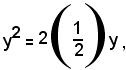
che differisce da un quadrato perfetto per la mancanza del termine
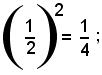
aggiungendo ad ambo i membri tale termine, si ha:
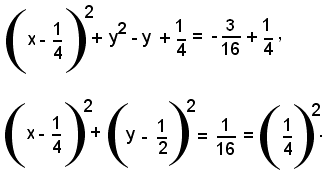
Confrontando questa equazione con la (2), si trova:
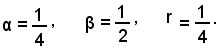
Circonferenze in posizione particolare
1)-Quando nell'equazione di una circonferenza manca il termine in x, la circonferenza ha il centro sull'asse y.
Esempio
L'equazione.
x2 + y2 - 4y + 3 = 0.
rappresenta una circonferenza avente il centro nel punto C(0, 2) e
2)-Quando nell'equazione di una circonferenza manca il termine in y, la circonferenza ha il centro sull'asse x.
Esempio
L'equazione
x2 + y2 - 6x + 8 = 0.
rappresenta una circonferenza avente il centro nel punto C(3, 0) e
3)-Quando nell'equazione di una circonferenza mancano i termini in x ed in y, la circonferenza ha il centro nell'origine degli assi.
Esempio
L'equazione
x2 + y2 - 9 = 0.
rappresenta una circonferenza avente di centro O(0, 0) e raggio r = 3.
Dunque, l'equazione della circonferenza avente per centro l'origine O e per raggio r è del tipo:
x2 + y2 = r2.
4)-Quando nell'equazione di una circonferenza mancano il termine noto, la circonferenza passa per l'origine.
Esempio
L'equazione
x2 + y2 - 6x - 8y = 0.
rappresenta una circonferenza passante per l'origine O(0, 0).
Infatti, le coordinate (0, 0) dell'origine soddisfano l'equazione data, cioè sostituendo nell'equazione data al posto della x e della y le coordinate (0, 0) dell'origine, si ha un'identità:
02 + 02 - 6· 0 - 8· 0 = 0.
Circonferenza sottoposta a determinate condizioni
L'equazione
x2 + y2 - 2αx - 2βy + γ = 0
della circonferenza di centro C(α, β) e raggio r dipende da tre coefficienti essenziali α, β, γ, a ciascuno dei quali si possono assegnare infiniti valori.
Per individuare una circonferenza, occorre quindi assegnare tre condizioni indipendenti.
Se si sottopone una circonferenza a tre condizioni indipendenti, queste si traducono in un sistema di tre equazioni nelle incognite α, β, γ che a seconda del grado determina uno o più cerchi.
Si esaminano ora le condizioni a cui può essere sottoposto un cerchio e si ricerca il loro grado.
a)-Condizione di passaggio di un cerchio per un punto, o di appartenenza di un punto ad un cerchio
Infatti, affinchè il punto P(x0, y0) appartenga al cerchio di equazione
x2 + y2 - 2αx - 2βy + γ = 0,
occorre che le sue coordinate rappresentino una soluzione dell'equazione del cerchio, cioè si verifichi:
x02 + y02 - 2αx0 - 2βy0 + γ = 0,
che è un'equazione di primo grado nelle incognite α, β, γ.
Nota bene
Si deve ricordare che l'equazione x2 + y2 - 2αx - 2βy + γ = 0 ammette infinite soluzioni ottenute assegnando ad una delle incognite, x o y, valori arbitrari e determinando poi, dopo aver sostituito nell'equazione tale valore arbitrario, l'altra incognita. Ogni soluzione dell'equazione rappresenta un punto della circonferenza.
Esempio - Circonferenza per tre punti
Determinare l'equazione della circonferenza passante per i punti A(2, 1), B(1, 0), C(-1,2), non allineati.

Per quanto detto in precedenza, il problema ammette una ed una sola soluzione, in quanto sono assegnate tre condizioni lineari indipendenti. Le tre condizioni si traducono in un sistema di primo grado di tre equazioni in tre incognite. Allo scopo, sia
x2 + y2 - 2αx - 2βy + γ = 0
l'equazione di una circonferenza generica.
I punti A, B, C appartengono alla circonferenza, se e solo se le loro coordinate soddisfano l'equazione della circonferenza.
Sostituendo successivamente nell'equazione al posto della x e della y le coordinate di A, B e C si ottengono tre equazioni nelle incognite α, β, γ:
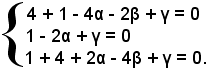
cioè
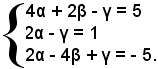
Per risolvere il sistema, conviene sommare la 2^ con la 3^ e la 1^ con la 3^ e determinare i valori di α e β che, sostituiti in una delle tre equazioni, danno i valori:
L'equazione cercata è:
x2 + y2 - x - 3y = 0.
Altro procedimento: il centro del cerchio richiesto dev'essere equidistante dai punti A, B, C; esso perciò si trova nel punto d'intersezione dell'asse del segmento AB con l'asse del segmento BC. L'asse del segmento AB ha equazione:
Elevando ambo i membri al quadrato e semplificando risulta:
x + y -2 = 0.
L'asse del segmento BC ha equazione:
Elevando ambo i membri al quadrato e semplificando risulta:
x - y + 1 = 0.
Si risolve ora il sistema:
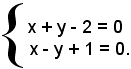
Le coordinate del centro del cerchio risultano:
Noto

il raggio è dato dalla distanza di O' da uno dei tre punti dati:
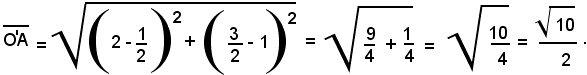
b)-Imporre ad un cerchio di avere un dato centro, equivale a dare due condizioni lineari, in quanto sono dati l'ascissa e l'ordinata del centro.
Esempio - Circonferenza di dato centro passante per un punto
Scrivere l'equazione di una circonferenza di centro C(3, 2) passante per il punto P(1, 2/3).
Il problema ammette una ed una sola soluzione, in quanto sono date tre condizioni lineari: due con l'ascissa e l'ordinata del centro e la terza con il passaggio per il punto P.

L'equazione della circonferenza si determina rapidamente sapendo che il raggio è dato dalla distanza di C da P, cioè:
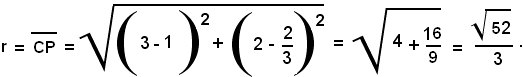
Applicando la (1), il cerchio richiesto di centro C e raggio r ha equazione:
sviluppando e riducendo, si ha:
c)-Imporre ad un cerchio di avere un dato raggio equivale ad assegnare una condizione di secondo grado.
Infatti, r2 = α2 + β2 - γ rappresenta un'equazione di secondo grado nelle incognite α, β, γ.
Esempio - Circonferenze di dato raggio passanti per due punti.
Scrivere le equazioni dei cerchi aventi raggio r = 3 passanti per i punti A(1, 3), B(4, 0).

Il problema ammette due soluzioni, in quanto delle tre condizioni date, due sono di primo grado, cioè il passaggio del cerchio per i punti A e B, l'altra di secondo grado è data dal raggio al quadrato; si hanno dunque due cerchi.
Sia data l'equazione di un cerchio generico:
x2 + y2 - 2αx - 2 βy + γ = 0,
affinchè esso passi per i punti A e B, occorre che le coordinate di tali punti soddisfino l'equazione del cerchio. Sostituendo nell'equazione alla x e alla y le coordinate di A e B, si hanno le prime due equazioni nelle incognite α, β, γ, cioè:
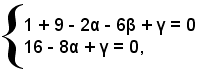
ossia
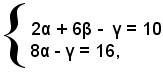
Il raggio del cerchio dev'essere uguale a 3; essendo r2 = α2 + β2 - γ, si ha la terza equazione
α2 + β2 - γ = 9.
Quindi il sistema di secondo grado da risolvere è:
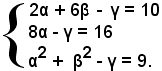
Per risolvere il sistema, si ricava α dalla prima x2 + y2 - x - 3y = 0 e si sostituisce il valore nelle altre due; si ricava β dalla seconda e si sostituisce il valore nelle altre due; infine si risolve l'equazione di secondo grado nell'incognita γ, ottenendo, dopo facili calcoli:
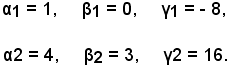
Le equazioni dei cerchi sono:
x2 + y2 - 2x - 8 = 0.
x2 + y2 - 8x - 6y + 16 = 0.
d)-Imporre ad un cerchio di essere tangente ad una retta in un punto assegnato equivale ad assegnare due condizioni lineari.
La prima condizione è che il cerchio passi per quel punto, la seconda p che il centro del cerchio si trovi sopra la normale per quel punto alla retta data.
Infatti, r2 = α2 + β2 - γ rappresenta un'equazione di secondo grado nelle incognite α, β, γ.
Esempio - Circonferenza tangente ad una retta in un punto dato e passante per quel punto.
Scrivere l'equazione della circonferenza tangente alla retta y + 1 = 0 nel punto A(0, -1) e passante per B(0, 3).

Il problema ammette una sola soluzione, in quanto sono date tre condizioni lineari. La prima che il cerchio passi per il punto A(0, -1); la seconda che il cerchio si trovi sulla perpendicolare alla retta y = -1 passante per A, cioè all'asse y e la terza il passaggio del cerchio per il punto B (0, 3).
Sia data l'equazione di un cerchio generico:
x2 + y2 - 2αx - 2βy + γ = 0.
Esso passa per il punto A(0, -1), se le coordinate del punto soddisfano l'equazione, cioè se si verifica:
1 + 2β + γ = 0.
Il cerchio è tangente alla retta y = -1 nel punto A(0, -1), se il centro si trova sulla perpendicolare per A alla retta y = -1.
Tale perpendicolare è l'asse y di equazione x = 0, cioè deve verificarsi α= 0.
Il cerchio passa per il punto B(0, 3) se:
Si risolve ora il sistema formato dalle tre relazioni:
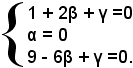
Si hanno i valori
α = 0, β = 1, γ = -3.
L'equazione del cerchio richiesto è:
x2 + y2 - 2y - 3 = 0.
Richiami
E' noto dalla geometria elementare che:
-una retta ha al massimo due punti in comune con una circonferenza, per questo si dice che la circonferenza è una curva del secondo ordine.
In generale si definisce ordine di una curva il numero delle intersezioni che la curva ha con una retta generica del piano.
-Le curve del primo ordine, rappresentate da equazioni di primo grado, si chiamano rette.
-Le curve del secondo ordine, rappresentate da equazioni di secondo grado nelle variabili x ed y si chiamano coniche.
-Le curve del terzo ordine, rappresentate da equazioni di terzo grado si chiamano cubiche.
-Le curve del quarto ordine, rappresentate da equazioni di quarto grado si chiamano quartiche, ecc.
Intersezioni di una retta con una circonferenza
Sia x2 + y2 - 2αx - 2βy + γ = 0 la circonferenza di centro C(α, β) e raggio r, y = mx + q una retta data, si vogliono determinare i punti comuni al cerchio e alla retta.
Le coordinate dei punti di intersezione del cerchio con la retta devono soddisfare l'equazione della retta, poichè tutti i punti stanno sulla retta; esse sono perciò le soluzioni del sistema formato dalle due equazioni:
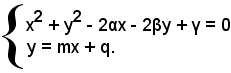
Se tale sistema ammette:
-due soluzioni reali e distinte, la retta ha due punti reali e distinti comuni con il cerchio, retta secante,
-se ha una soluzione, cioè due soluzioni reali e coincidenti, la retta ha un punto, cioè due punti coicidenti, in comune con il cerchio, retta tangente,
-se non ha soluzioni reali, la retta non ha punti comuni con il cerchio, retta esterna.
Esempi
1)-Determinare le intersezioni della retta x + 2y - 4 = 0 con la circonferenza di equazione:
x2 + y2 - 4x = 0.
Si deve risolvere il sistema:
Si deve risolvere il sistema:
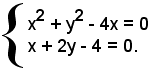
Sostituendo nella prima equazione il valore
ricavato dalla seconda, si ha:
Le soluzioni del sistema sono:
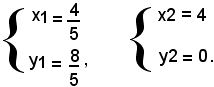
I punti
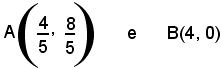
sono punti comuni al cerchio e alla retta.
La retta x + 2y - 4 = 0 è secante il cerchio x2 + y2 - 4x = 0.
Infatti, la distanza dal centro C(2, 0) del cerchio dalla retta è:
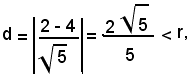
essendo
r = 2.
2)-Determinare le intersezioni della retta x - 3y + 2 = 0 con la circonferenza di equazione:
Si osservi che la retta è tangente alla circonferenza in quanto la distanza del centro C(2, -2) della circonferenza dalla retta è uguale al raggio.
Si ricordi che se una retta è rispettivamente secante, tangente, esterna ad un cerchio, la sua distanza dal centro del cerchio è rispettivamente minore, uguale o maggiore del raggio.
Infatti, si ha:
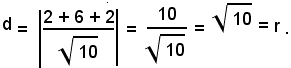
Per determinare le coordinate del punto di contatto o di tangenza della retta con la circonferenza si risolve il sistema formato dalle due equazioni:
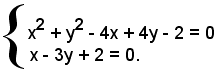
Sostituendo nella prima equazione il valore di x = 3y - 2, ricavato dalla seconda, si ha y1 = y2 = 1.
Le soluzioni del sistema sono:
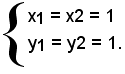
Le coordinate del punto di contatto con la retta x - 3y + 2 = 0 con la circonferenza x2 + y2 - 4x + 4y - 2 = 0 sono (1, 1).
La retta è quindi tangente alla x2 + y2 - 4x + 4y - 2 = 0 nel punto (1, 1).
Nota bene
Si è detto che una retta è tangente ad una circonferenza quando ha in comune con essa due punti reali e coincidenti. Questa proprietà si estende, salvo eccezioni, ad una curva qualsiasi. Se due fra le intersezioni di una retta con una curva coincidono in un punto, la retta è tangente alla curva in quel punto. Che il punto di contatto A di una retta tangente ad una curva debba considerarsi come due punti di contatto, si rileva dal fatto che la tangente rappresenta la posizione limite della corda AB quando B tende a coincidere con A, come in figura 1, sempre che il punto A sia un punto semplice per la curva.
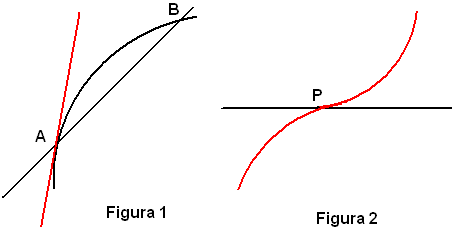
Un punto P per una curva si dice semplice quando qualsiasi retta passante per esso assorba in P una sola intersezione tra quelle che la retta ha con la curva. Per tale motivo si dice che la retta tangente ha un contatto bipunto con la curva oppure che la tangente tocca la curva.
Fa eccezione il caso in cui P sia punto di flesso, in quanto la tangente ha un contatto tripunto, pur essendo il punto semplice, come da figura 2.
3)-Determinare le intersezioni della circonferenza di equazione x2 + y2 - 4x + 3 = 0 con la retta x - y + 1 = 0.
Si osservi che la retta è esterna alla circonferenza in quanto la sua distanza del centro C(2, 0) del cerchio dalla retta è maggiore al raggio.
Infatti, si ha:

essendo r = 1.
Allora Il sistema formato dalle due equazioni:
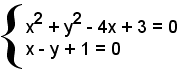
non deve ammettere soluzioni nel campo reale.
Infatti, sostituendo nella prima equazione il valore di y = x + 1, ricavato dalla seconda, si ha:
x2 - x + 2 = 0.
Quest'equazione non ha radici reali perchè il suo discriminante
Δ = 1 - 8 = - 7 < 0.
Tangente ad un cerchio in un suo punto - Formula di sdoppiamento
Sia data la circonferenza di equazione x2 + y2 - 2αx - 2βy + γ = 0 di centro C(α, β), raggio r e P(x0, y0) un suo punto; si vuole determinare l'equazione della tangente alla circonferenza nel punto P(x0, y0).
L'equazione della retta che passa per P(x0, y0) ed ha per coefficiente angolare l'opposto e reciproco di m è:
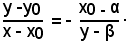
Liberando dai denominatori ed ordinando, si ha:
(6) xx0 + yy0 - αx - βy - (x02 + y02 - αx0 - βy0) = 0.
Poichè P(x0, y0) è un punto della circonferenza, le sue coordinate devono soddisfare l'equazione della circonferenza:
x02 + y02 - 2αx0 - 2βy0 + γ = 0,
ossia
x02 + y02 - αx0 - αx0 - βy0 - βy0 + γ = 0,
cioè
x02 + y02 - αx0 - βy0 = αx0 + βy0 - γ
Sostituendo nella (6) tale valore ed ordinando, si ottiene:
(7) xx0 + yy0 - α(x + x0) - β(y - y0) + γ = 0.
Si rileva come l'equazione della tangente nel punto P(x0, y0) alla circonferenza x2 + y2 - 2αx - 2βy + γ = 0 si ottenga rapidamente ponendo xx0 al posto di x2, yy0 al posto di y2,

al posto di x,
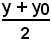
al posto di y.
La (7) si chiama formula di sdoppiamento.
Se l'equazione della circonferenza è data sotto la forma:
(x - α)2 + (y - β)2 = r2,
in tal caso la formula di sdoppiamento si scrive:
(x - α)(x0 - α) + (y - β)(y0 - β) = r2.
Esempi
1)-Determinare l'equazione della tangente nel punto P(5, 8) alla circonferenza x2 + y2 - 4x - 8y - 5γ - 5 = 0.
La tangente richiesta è la perpendicolare alla retta CP per il punto P. Le coordinate del centro C della circonferenza sono α = 2 e β = 4.
Il coefficiente angolare della retta CP è:
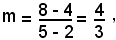
mentre il coefficiente della tangente è - 3/4.
L'equazione della tangente è quella della retta che passa per P ed ha coefficiente angolare -3/4, cioè:
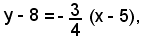
ossia
3x + 4y - 47 = 0.
Applicando direttamente la formula di sdoppiamento, si ottiene:
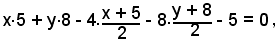
ove si è sostituito nell'equazione x2 + y2 - 4x - 8y - 5γ - 5 = 0 della circonferenza, a x2 il valore x · 5, a y2 il valore y · 8, a x il valore
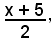
a y il valore
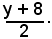
Ordinando l'equazione della tangente in P(5, 8) alla circonferenza data, risulta:
5x - 4y - 47 = 0.
2)-Determinare l'equazione della tangente alla circonferenza x2 + y2 - 4x - 8y = 0 nell'origine delle coordinate.
Applicando la formula di sdoppiamento, si ha:
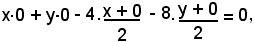
- 2x - 4y = 0,
ossia
x + y = 0.
Si rilevi come tale equazione si ottiene uguagliando a zero il complesso dei termini di primo grado dell'equazione della circonferenza.
Infatti, il complesso dei termini di primo grado dell'equazione della circonferenza è - 4x - 8y = 0, che uguagliato a zero dà:
4x + 8y = 0,
ossia
x + 2y = 0.
In generale, sussiste la proprietà:
-l'equazione della retta tangente nell'origine ad un cerchio passante per l'origine, si ottiene uguagliando a zero il complesso dei termini di primo grado nell'equazione del cerchio.
Tale proprietà si estende a tutte le curve algebriche.
Una curva si dice algebrica quando la sua equazione può ridursi ad un polinomio algebrico uguagliato a zero, per esempio x3 - xy + y3 - x - 1= 0.
Una curva non algebrica si chiama trascendente, per esempio y = senx, y = tgx, y = logx, y = ax, ecc.
Una curva algebrica passa per l'origine quando nella sua equazione manca il termine noto e l'equazione della tangente alla curva nell'origine si ottiene uguagliando a zero il complesso dei termini di primo grado.
Per esempio la curva di equazione x3 + y3 - x = 0 passa per l'origine ed ha ivi per tangente la retta di equazione x =0.
Tangenti per un punto ad una circonferenza
Esempi
1)-Scrivere le equazioni delle tangenti al cerchio x2 + y2 - 4x + 4y - 2 = 0 uscenti dal punto P(4, 2).
Primo procedimento
Si scrive l'equazione di una retta generica passante per P(4, 2):
y - 2 = m(x - 4)
e s'impone che le due intersezioni della retta con il cerchio coincidano, cioè le radici dell'equazione di secondo grado in x, o y, risolvente del sistema
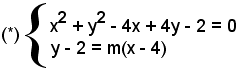
siano reali e coincidenti.
Affinchè l'equazione
(1 + m2)x2 - 4(2m2 - 2m + 1)x + 16m2 - 32m + 10 = 0,
ottenuta sostituendo nella prima equazione del sistema (*) il valore della y ricavato dalla seconda, abbia radici reali e coincidenti occorre che il discriminante sia uguale a zero, cioè:
Δ = 4(2m2 - 2m + 1)2 - (1 + m2)(16m2 - 32m + 10) = 0.
Sviluppando e ordinando, si ha:
3m2 + 8m - 3 = 0,
da cui
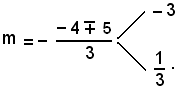
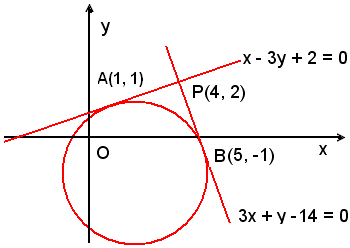
Le equazioni delle tangenti al cerchio dal punto P(4, 2) sono:
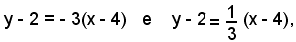
cioè
3x + y - 14 = 0 e x - 3y + 2 = 0.
Ricordando che un punto P(x0, y0) è esterno, appartiene o è interno al cerchio (x - α)2 + (y - β)2 = r2, a seconda che la sua distanza dal centro sia rispettivamente maggiore, uguale o minore del raggio.
Analiticamente ciò viene espresso dalla relazione:

Pertanto, si può verificare che il punto P(4, 2) è esterno al cerchio.
Infatti, la distanza di P(4, 2) dal centro C(2, -2) è:
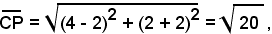
ed essendo il raggio
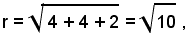
risulta
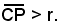
I punti di contatto delle rette tangenti con il cerchio hanno coordinate rispettivamente A(1, 1) e B(-5, 1).
Secondo procedimento
Per scrivere le equazioni delle tangenti al cerchio x2 + y2 - 4x + 4y - 2 = 0 uscenti dal punto P(4, 2), si considera una generica retta uscente dal punto P(4, 2), la cui equazione è:
y - 2 = m(x - 4)
e s'impone che abbia distanza dal centro C(2, -2) di un segmento uguale al raggio

del cerchio.
Per la nota formula della distanza, si trova la condizione:
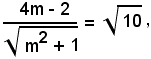
elevando al quadrato ed ordinando, si ha
3m2 + 8m - 3 = 0,
da cui
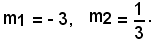
Sostituendo ad m tali valori nell'equazione y - 2 = m(x - 4), si hanno le equazioni delle tangenti al cerchio uscenti dal punto P(4, 2), cioè le equazioni:
3x + y - 14 = 0 e x - 3y + 2 = 0.
I due procedimenti esposti possono essere utilizzati per determinare la tangente al cerchio in un suo punto, per quanto sia preferibile, par la rapidità di calcolo, la formula (7):
(7) xx0 + yy0 - α(x + x0) - β(y - y0) + γ = 0.
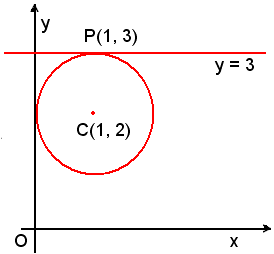
2)-Trovare la tangente alla circonferenza x2 + y2 - 2x - 4y + 4 = 0 nel suo punto P(1, 3).
Primo procedimento
Si scrive l'equazione di una retta generica passante per P(1, 3) e si cercano le intersezioni di questa con il cerchio, una è P, e s'impone che coincidano. l'equazione del fasci di rette di centro P è:
y - 3 = m(x -1);
le coordinate dei punti di intersezione si trovano risolvendo il sistema:
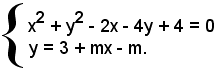
Queste coincidono se le radici dell'equazione risolvente:
(1 + m2)x2 - 2(m2 - m + 1)x + m2 - 2m + 1 = 0,
ottenuta sostituendo nella prima equazione del sistema il valore della y ricavato dalla seconda, abbia radici reali e coicidenti occorre che il discriminante sia uguale a zero, cioè:
Δ = (m2 - m + 1)2 - (1 + m2)(m2 - 2m + 1) = 0,
Sviluppando, ordinando e risolvendo, si ha:
m2 = 0,
da cui
m1 = m2 = 0.
Sostituendo tale valore nell'equazione y = 3 + mx - m, si ha l'equazione cercata: y = 3.
Secondo procedimento
Si scrive l'equazione di una generica retta per P(1, 3) e s'impone che abbia distanza dal centro C(1, 2) di un segmento uguale al raggio r =1.
L'equazione di una retta generica per P(1, 3) è:
y - 3 = m(x - 1),
ossia
mx - y - m + 3 = 0;
la distanza della retta dal centro C(1, 2) dev'essere uguale a 1, quindi:
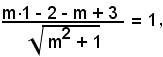
da cui
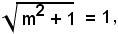
ossia
L'equazione della retta tangente al cerchio nel punto P(1, 3) è y - 3 = 0.
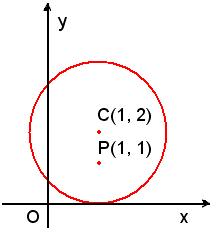
3)-Trovare le equazioni delle tangenti al cerchio x2 + y2 - 2x - 4y + 1 = 0 uscenti dal punto P(1, 1), interno ad esso.
Infatti, si verifica che il punto P è interno al cerchio: sostituendo nell'equazione del cerchio ad x ed y i valori 1 e 1, ascissa e ordinata di P, si ha
1 + 1 - 2 - 4 + 1 = -3 < 0,
cioè la distanza di P da C è minore di r.
Tale risultato si riscontra applicando i due procedimenti svolti negli esempi precedenti.
Riassumendo i risultati dei tre esempi, si può affermare che:
-il problema di condurre da un punto dato le tangenti ad un cerchio dato, ammette due soluzioni reali e distinte quando il punto è esterno al cerchio, due soluzioni reali e coincidenti quando il punto sta sul cerchio, due soluzioni immaginarie e coniugate quando il punto è interno al cerchio.
COMPLEMENTI
Potenza di un punto rispetto a un cerchio
Siano dati il cerchio di equazione x2 + y2 - 2αx - 2βy + γ = 0 ed il punto P(x0, y0).Definizione - Si chiama potenza di P rispetto al cerchio di centro C(α, β) e raggio r, e si indica con p, la differenza:
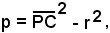
ossia
(8) p = (x0 - α)2 + (y0 - β)2 - r2,
essendo
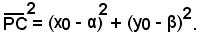
Si può dunque affermare che:
-la potenza del punto P(x0, y0) rispetto al cerchio di equazione x2 + y2 - 2αx - 2βy + γ = 0 è uguale, in valore e segno, al primo membro dell'equazione della circonferenza scritta in forma normale, quando al posto delle coordinate correnti x ed y, si sostituiscono le coordinate del punto.
I punti esterni al cerchio hanno potenza positiva, mentre quelli interni hanno potenza negativa.Infatti, se P(x0, y0) è esterno al cerchio x2 + y2 - 2αx - 2βy + γ = 0, si ha:
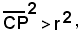
cioè
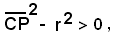
da cui
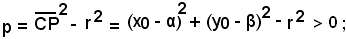
se P(x0, y0) è interno al cerchio x2 + y2 - 2αx - 2βy + γ = 0, si ha:
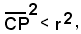
cioè
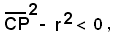
da cui
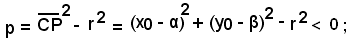
i punti appartenenti al cerchio hanno potenza nulla; il cerchio dunque è il luogo geometrico dei punti del piano aventi rispetto ad esso potenza nulla.
Esempio - Determinare il valore della potenza del punto P(1, 2) rispetto al cerchio di equazione x2 + y2 - 4x + 2y + 1 = 0.
Applicando la (8), si ha:
12 + 22 - 4 · 1 + 2 · 2 + 1 = 6 > 0.
ll punto P è esterno al cerchio, essendo la sua potenza positiva.
Infatti, il punto P ha dal centro distanza maggiore del raggio.
Essendo:
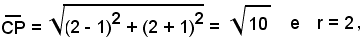
si ha:
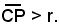
Si verifica come il valore 6, potenza di P(1, 2) rispetto al cerchio dato, rappresenti il prodotto delle distanze di P dalle intersezioni con il cerchio di una retta uscente da P. Allo scopo, si considera la retta uscente da P di coefficiente angolare 3 e si determinano le coordinate dei punti A e B, intersezioni di tale retta con il cerchio dato.
Risolvendo il sistema:
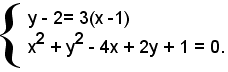
si trovano le coordinate di A , 0 E - 1, e le coordinate di B, 2/5 E 1/5.
Il prodotto della distanze di P da A e B è dato da:
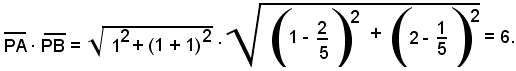
Dopo aver ripetuto il calcolo per la retta che esce da P, che è parallela all'asse y, si ha che i punti di contatto T e T' delle tangenti, come si e visto, condotte da P al cerchio hanno coordinate:
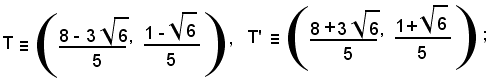
per cui
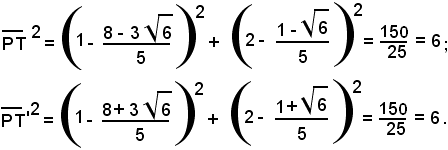
Si è così verificato che:
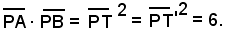
Asse radicale di due cerchi - Fasci di cerchi - Asse centrale
Siano date due circonferenze di equazioni:
x2 + y2 - 2αx - 2βy + γ = 0,
x2 + y2 - 2α'x - 2β'y + γ' = 0.
Le coordinate dei punti di intersezione sono date dalla soluzione del sistema:
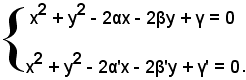
Tale sistema è di quarto grado ed è equivalente al sistema di secondo grado seguente:
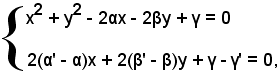
le cui soluzioni forniscono le coordinate dei due punti reali A e B.
Si ricordi che il grado di un sistema di equazioni algebriche è dato dal prodotto dei gradi delle equazioni componenti.
La retta di equazione:
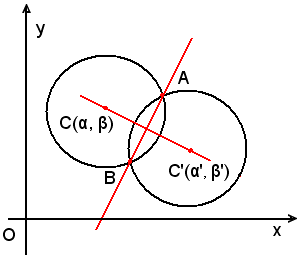
L'asse radicale è la retta AB, che congiunge i due punti reali A e B in cui si intersecano i cerchi dati.
Tale retta rappresenta il luogo geometrico dei punti che hanno uguale potenza rispetti ai cerchi stessi.
Infatti, se si indica con P un punto generico del piano di coordinate x ed y, la sua potenza rispetto al primo cerchio è uguale al primo membro della sua equazione; la sua potenza rispetto al secondo cerchio è uguale al primo membro della seconda equazione; affinchè P abbia la stessa potenza rispetto ai due cerchi, dev'essere:
x2 + y2 - 2α'x - 2β'y + γ' = x2 + y2 - 2αx - 2βy + γ,
da cui trasportando tutto nel secondo membro, si ha l'equazione dell'asse radicale.
2(α' - α)x + 2(β' - β)y + γ - γ' = 0.
Se i due cerchi sono secanti, l'asse radicale è dato dalla retta AB, che congiunge i punti A e B; se i due cerchi sono tangenti, l'asse radicale è la tangente comune ai due cerchi; se i due cerchi sono esterni, l'asse radicale è esterno ad entrambi i cerchi.
Costruzione dell'asse radicale di due cerchi esterni
Per costruire l'asse radicale di due cerchi esterni α e β, si considera un terzo cerchio γ secante entrambi; si determina l'asse radicale dei cerchi α e γ e l'asse radicale dei cerchi β e γ. Essi s'incontrano in un punto M, la perpendicolare per M alla retta congiungente i centri dei due cerchi dati α e β, asse centrale, dà l'asse radicale richiesto.
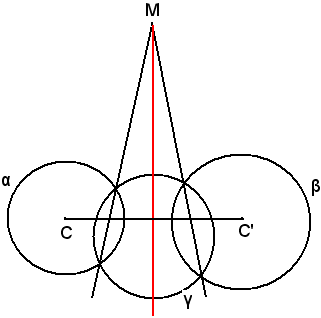
Gli infiniti cerchi passanti per i punti A e B, punti di intersezione di due cerchi dati, costituiscono il fascio di cerchi. L'equazione del fascio di cerchi si ottiene facendo una combinazione lineare dei cerchi dati, cioè sommando la prima equazione con la seconda moltiplicata per un parametro λ.
Essa è del tipo:
x2 + y2 - 2αx - 2βy + γ + λ(x2 + y2 - 2α'x - 2β'y + γ') = 0,
ossia
(1 + λ)(x2 + y2) - 2(α + λα')x - 2(β + λβ')y + γ + λγ' = 0,
da cui
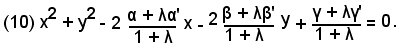
La retta congiungente i centri C(α, β) C'(α', β') si chiama asse centrale. La sua equazione è:
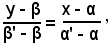
ossia, sviluppando e riducendo,
(11) (β' - β)x - (α' - α)y + α'β - αβ' = 0.
Si rileva facilmente come l'asse centrale sia perpendicolare all'asse radicale.
Infatti, è soddisfatta la condizione di perpendicolarità delle due rette:
2(β' - β)(α' - α) - 2(α' - α)(β' - β) = 0.
Nota bene
Si vedrà in seguito che:
-viceversa, data l'equazione di un fascio di cerchi, le equazioni dei due cerchi fondamentali si ottengono ponendo λ = 0 e λ = ∞ nell'equazione (10).
Per λ = - 1, la (10) fornisce l'equazione dell'asse radicale, poichè per ogni valore di λ la (10) dà un cerchio passante per i punti dase del fascio A e B, L'asse radicale può considerarsi come un cerchio limite del fascio, che ha raggio infinito.
Esempi
1)-Scrivere l'equazione dell'asse radicale dei cerchi:
α) x2 + y2 - 2x - 2y - 2 = 0,
β) x2 + y2 - 8x + 4y + 4 = 0;
verificare inoltre che esso è il luogo dei punti che hanno uguale potenza rispetto ai cerchi stessi.
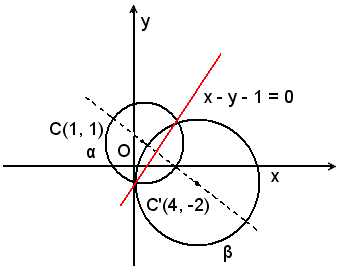
Sottraendo le equazioni dei due cerchi α e β, si ha l'equazione dell'asse radicale; essa è:
x - y - 1 = 0.
Per verificare che ogni punto dell'asse radicale ha la stessa potenza rispetto ai cerchi α e β, si indicano con x ed y le coordinate di un generico punto P. La potenza del punto P rispetto al cerchio di equazione α è uguale a x2 + y2 - 2x - 2y - 2; la potenza del punto P rispetto al cerchio di equazione β è uguale a x2 + y2 - 8x + 4y + 4.
Affinchè il punto P abbia la stessa potenza rispetto ai due cerchi occorre che sia:
x2 + y2 - 2x - 2y - 2 = x2 + y2 - 8x + 4y + 4.
Trasportando tutto al primo membro e semplifIcando, si ottiene:
x - y - 1 = 0,
condizione di appartenenza del punto P(x, y) alla retta x - y - 1 = 0.
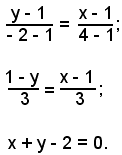
Si rileva che l'asse centrale è perpendicolare all'asse radicale, in quanto è soddisfatta la condizione di perpendicolarità.
2)-Trovare il cerchio che passa per le intersezioni dei cerchi x2 + y2 - 1 = 0 e x2 + y2 + 2x = 0 e per il punto P.
Il problema ammette una sola soluzione, in quanto si deve determinare un cerchio passante per tre punti, cioè per i due punti comuni ai cerchi dati e per il punto P.
Gli infiniti cerchi passanti per i punti comuni dei cerchi dati hanno equazione:
(1 + λ)(x2 + y2) - 1 + 2λx = 0,
ottenuta facendo una combinazione lineare delle equazioni dei due cerchi, cioè sommando la prima con la seconda equazione moltiplicata per il parametro λ.
Dividendo l'equazione del fascio per 1 + λ, si ottiene l'equazione del fascio in forma normale:
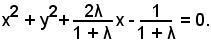
Un cerchio del fascio passa per il punto P(3, 2), se le coordinate di P soddisfano tale equazione, cioè se si verifica:
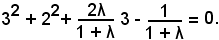
Risolvendo rispetto a λ, si ha:
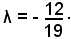
Sostituendo tale valore in
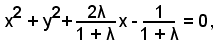
si ottiene l'equazione del cerchio richiesto:
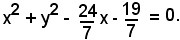
3)-Scrivere l'equazione del cerchio passante per i punti comuni al cerchio x2 + y2 - 4x + 2y + 1 = 0 e x2 + y2 + 2x = 0 e alla retta 3x - y + 5 = 0 e per l'origine della coordinate.
Si ricordi che si definiscono "fascio di cerchi" gli infiniti cerchi passanti per due punti.
Quindi, per i punti comuni al cerchio e alla retta passano infiniti cerchi, il cui asse radicale è la stessa retta.
-viceversa, data l'equazione di un fascio di cerchi, le equazioni dei due cerchi fondamentali si ottengono ponendo λ = 0 e λ = ∞ nell'equazione (10).
Per λ = -1, la (10) fornisce l'equazione dell'asse radicale, poichè per ogni valore di λ la (10) dà un cerchio passante per i punti dase del fascio A e B. L'asse radicale può considerarsi come un cerchio limite del fascio, che ha raggio infinito.
L'equazione del fascio si ottiene facendo la combinazione lineare delle equazioni date, cioè sommando la prima equazione con la seconda moltiplicata per il parametro λ. Essa è:
x2 + y2 - 4x + 2y + 1 + λ(3x - y + 5) = 0,
ossia
x2 + y2 - (4 - 3λ)x + (2 - λ)y + 1 + 5λ = 0.
Per trovare il cerchio del fascio che passa per l'origine, basta uguagliare a zero il termine noto, cioè
1 + 5λ = 0,
da cui λ = -7/5; sostituendo tale valore nell'equazione del fascio, si trova l'equazione del cerchio richiesto:
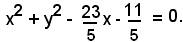
Dato il fascio di cerchi x2 + y2 - 2x + λ(x2 + y2 - 3y) = 0, determinare:
a)-i cerchi fondamentali:
b)-i cerchi del fascio che hanno raggio 1.
a)-I cerchi fondamentali del fascio si ottengono per i valori particolari del parametro λ: per λ = 0 e λ = ∞. Per λ = 0, si ha il cerchio x2 + y2 - 2x = 0.
Si divide ora l'equazione del fascio per λ e si ricordi che una frazione con denominatore infinito è uguale a zero.
Per λ = ∞, si ha:
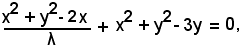
ossia
x2 + y2 - 3y = 0.
b)-Il centro del generico cerchio del fascio:
x2 + y2 - 2x + λ(x2 + y2 - 3y) = 0,
ossia ordinando e riducendo tale equazione in forma normale
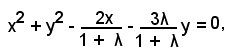
ha coordinate
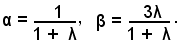
Ricordando che:

si ha
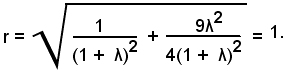
Elevando al quadrato ambo i membri e riducendo, si ha:
5λ2+ λ= 0,
da cui
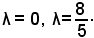
Sostituendo tali valori nell'equazione del fascio, si hanno le equazioni dei due cerchi:
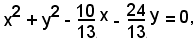
Polare di un punto rispetto a un cerchio
Si riprende l'esempio visto per le tangenti a un cerchio in un punto, per trovare una soluzione più semplice.
In tale esempio si chiedeva di scrivere le equazioni delle tangenti al cerchio x2 + y2 - 4x + 4y - 2 = 0 uscenti dal punto P(4, 2).
Supponendo di aver risolto il problema, si indicano con a e b le tangenti al cerchio uscenti da P e con T e T' i rispettivi punti di contatto, come in figura.
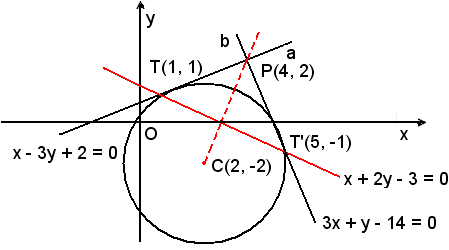
Quindi, le tangenti a e b sono le rette congiungenti il punto P con i punti T e T'.
I punti T e T' sono i punti di intersezione della retta TT' con il cerchio.
La retta TT', che si indica con p, si chiama polare del punto P rispetto al cerchio e P polo.
La sua equazione è:
x + 2y - 3 = 0,
ottenuta applicando la formula di sdoppiamento, cioè sostituendo nell'equazione del cerchio dato 4x ad x2, 2y ad y2, (x+4)/2 ad x, (y + 2)/2 ad y.
La retta TT' coincide con p, polare di P rispetto al cerchio la si può definire così:
-retta congiungente i punti di contatto delle tangenti condotte dal punto al cerchio.
Le coordinate T e T' sono date dalla soluzione del sistema:
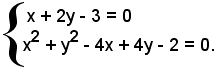
Esse sono T(1, 1) e T'(5, -1).
Le due tangenti a e b, rette congiungenti rispettivamente i punti P, T e P, T' hanno equazioni:
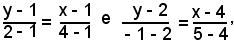
ossia
a) x - 3y + 2 = 0 e 3x + y - 14 = 0.
Poichè la retta TT', coincidente con p, si è ottenuta applicando l'equazione (7) con la formula di sdoppiamento, si può affermare che l'equazione della polare di un punto P rispetto ad un cerchio coincide con l'equazione della tangente al cerchio, se P appartiene ad esso, cioè:
-la polare di un punto del cerchio è la tangente ad esso in quel punto.
In conclusione:
-se il punto P è esterno al cerchio, la polare è secante ad esso ed è la retta congiungente i punti di contatto delle tangenti condotte dal punto al cerchio;
-se P è un punto del cerchio, la polare coincide con la tangente in P;
-se P è un punto interno al cerchio, la polare è esterna.
Si osservi come la polare di P rispetto al cerchio sia perpendicolare alla retta CP.
Infatti, la polare di P rispetto al cerchio dato ha coefficiente angolare m = -1/2 e la retta CP ha coefficiente angolare m' = (2 + 2)/(4 - 2) = 2.
Si ricorda che la condizione di perpendicolarità fra due rette è che il prodotto dei coefficienti è uguale a -1.
Si osserva ancora come il prodotto delle distanze del polo e della polare dal centro del cerchio sia uguale al quadrato del raggio.
Infatti, la distanza

e la distanza della retta TT' da C è:
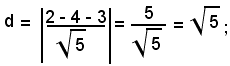
dunque:
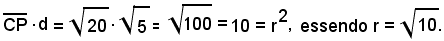
Mediante le proprietà enunciate si può costruire la polare di un punto rispetto al cerchio.
Se il punto P è esterno al cerchio, si conducono le tangenti da P al cerchio, la retta congiungente i punti di contatto è la polare di P richiesta.
Se P appartiene al cerchio la polare è la tangente in P ad esso.
Se P è interno al cerchio, la sua polare si costruisce nel modo seguente, come in figura.
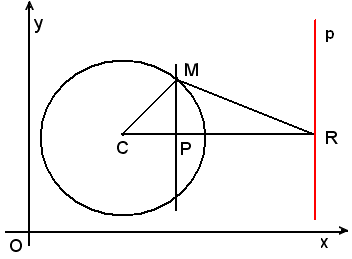
Per P si conducono la perpendicolare fino ad incontrare in M il cerchio, la tangente in M ad esso incontra la CP in R, la perpendicolare per R alla CP è la polare del polo P.
Si osservi che tale costruzione è fatta in base alla proprietà enunciata per i triangoli rettangoli.
Infatti, dal triangolo rettangolo CMR, per il Teorema di Euclide, si ha:
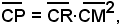
ossia
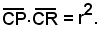
In generale, l'equazione della polare nel punto P(x0, y0) rispetto al cerchio
x2 + y2 - 2αx - 2 βy + γ = 0,
applicando la formula di sdoppiamento, è:
(12) xx0 + yy0 - α(x + x0) - β(y + y0) + γ = 0.
Si può concludere che:
la (12) rappresenta l'equazione della tangente in P(x0, y0) al cerchio x2 + y2 - 2αx - 2βy + γ = 0, se il punto P appartiene al cerchio; è invece l'equazione della polare di P rispetto al cerchio, se P non appartiene al cerchio, cioè la (12), in ogni caso, rappresenta l'equazione della retta congiungente i punti di contatto delle tangenti condotte dal punto al cerchio.
La retta è quindi tangente alla x2 + y2 - 4x + 4y - 2 = 0 nel punto (1, 1).
Nota bene
Si è detto che una retta è tangente ad una circonferenza quando ha in comune con essa due punti reali e coincidenti. Questa proprietà si estende, salvo eccezioni, ad una curva qualsiasi. Se due fra le intersezioni di una retta con una curva coincidono in un punto, la retta è tangente alla curva in quel punto. Che il punto di contatto A di una retta tangente ad una curva debba considerarsi come due punti di contatto, si rileva dal fatto che la tangente rappresenta la posizione limite della corda AB quando B tende a coincidere con A, come in figura 1, sempre che il punto A sia un punto semplice per la curva.

Un punto P per una curva si dice semplice quando qualsiasi retta passante per esso assorba in P una sola intersezione tra quelle che la retta ha con la curva. Per tale motivo si dice che la retta tangente ha un contatto bipunto con la curva oppure che la tangente tocca la curva.
Fa eccezione il caso in cui P sia punto di flesso, in quanto la tangente ha un contatto tripunto, pur essendo il punto semplice, come da figura 2.
3)-Determinare le intersezioni della circonferenza di equazione x2 + y2 - 4x + 3 = 0 con la retta x - y + 1 = 0.
Si osservi che la retta è esterna alla circonferenza in quanto la sua distanza del centro C(2, 0) del cerchio dalla retta è maggiore al raggio.
Infatti, si ha:

essendo r = 1.
Allora Il sistema formato dalle due equazioni:
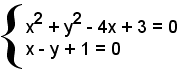
non deve ammettere soluzioni nel campo reale.
Infatti, sostituendo nella prima equazione il valore di y = x + 1, ricavato dalla seconda, si ha:
x2 - x + 2 = 0.
Quest'equazione non ha radici reali perchè il suo discriminante
Δ = 1 - 8 = - 7 < 0.
Tangente ad un cerchio in un suo punto - Formula di sdoppiamento
Sia data la circonferenza di equazione x2 + y2 - 2αx - 2βy + γ = 0 di centro C(α, β), raggio r e P(x0, y0) un suo punto; si vuole determinare l'equazione della tangente alla circonferenza nel punto P(x0, y0).
Si sa che la tangente alla circonferenza è perpendicolare al raggio che passa per il punto di contatto; allora la retta che passa per il punto P(x0, y0), il cui coefficiente angolare è uguale all'opposto e reciproco di quello del raggio passante per P, è la retta tangente alla circonferenza nel suo punto P(x0, y0).
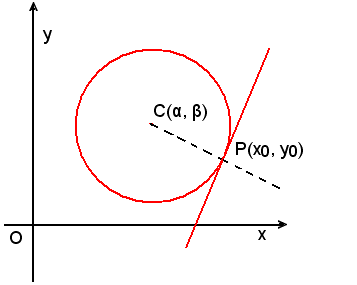
Ricordando che il coefficiente angolare della retta congiungente due punti è dato dal rapporto fra la differenza delle ordinate e la differenza delle ascisse, nel caso specifico, si ha che Il coefficiente angolare della retta CP è:
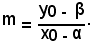

Ricordando che il coefficiente angolare della retta congiungente due punti è dato dal rapporto fra la differenza delle ordinate e la differenza delle ascisse, nel caso specifico, si ha che Il coefficiente angolare della retta CP è:
L'equazione della retta che passa per P(x0, y0) ed ha per coefficiente angolare l'opposto e reciproco di m è:
Liberando dai denominatori ed ordinando, si ha:
(6) xx0 + yy0 - αx - βy - (x02 + y02 - αx0 - βy0) = 0.
Poichè P(x0, y0) è un punto della circonferenza, le sue coordinate devono soddisfare l'equazione della circonferenza:
x02 + y02 - 2αx0 - 2βy0 + γ = 0,
ossia
x02 + y02 - αx0 - αx0 - βy0 - βy0 + γ = 0,
cioè
x02 + y02 - αx0 - βy0 = αx0 + βy0 - γ
Sostituendo nella (6) tale valore ed ordinando, si ottiene:
(7) xx0 + yy0 - α(x + x0) - β(y - y0) + γ = 0.
Si rileva come l'equazione della tangente nel punto P(x0, y0) alla circonferenza x2 + y2 - 2αx - 2βy + γ = 0 si ottenga rapidamente ponendo xx0 al posto di x2, yy0 al posto di y2,
al posto di x,
al posto di y.
La (7) si chiama formula di sdoppiamento.
Se l'equazione della circonferenza è data sotto la forma:
(x - α)2 + (y - β)2 = r2,
in tal caso la formula di sdoppiamento si scrive:
(x - α)(x0 - α) + (y - β)(y0 - β) = r2.
Esempi
1)-Determinare l'equazione della tangente nel punto P(5, 8) alla circonferenza x2 + y2 - 4x - 8y - 5γ - 5 = 0.
La tangente richiesta è la perpendicolare alla retta CP per il punto P. Le coordinate del centro C della circonferenza sono α = 2 e β = 4.
Il coefficiente angolare della retta CP è:
mentre il coefficiente della tangente è - 3/4.
L'equazione della tangente è quella della retta che passa per P ed ha coefficiente angolare -3/4, cioè:
ossia
3x + 4y - 47 = 0.
Applicando direttamente la formula di sdoppiamento, si ottiene:
ove si è sostituito nell'equazione x2 + y2 - 4x - 8y - 5γ - 5 = 0 della circonferenza, a x2 il valore x · 5, a y2 il valore y · 8, a x il valore
a y il valore
Ordinando l'equazione della tangente in P(5, 8) alla circonferenza data, risulta:
5x - 4y - 47 = 0.
2)-Determinare l'equazione della tangente alla circonferenza x2 + y2 - 4x - 8y = 0 nell'origine delle coordinate.
Applicando la formula di sdoppiamento, si ha:
ossia
x + y = 0.
Si rilevi come tale equazione si ottiene uguagliando a zero il complesso dei termini di primo grado dell'equazione della circonferenza.
Infatti, il complesso dei termini di primo grado dell'equazione della circonferenza è - 4x - 8y = 0, che uguagliato a zero dà:
4x + 8y = 0,
ossia
x + 2y = 0.
In generale, sussiste la proprietà:
-l'equazione della retta tangente nell'origine ad un cerchio passante per l'origine, si ottiene uguagliando a zero il complesso dei termini di primo grado nell'equazione del cerchio.
Tale proprietà si estende a tutte le curve algebriche.
Una curva si dice algebrica quando la sua equazione può ridursi ad un polinomio algebrico uguagliato a zero, per esempio x3 - xy + y3 - x - 1= 0.
Una curva non algebrica si chiama trascendente, per esempio y = senx, y = tgx, y = logx, y = ax, ecc.
Una curva algebrica passa per l'origine quando nella sua equazione manca il termine noto e l'equazione della tangente alla curva nell'origine si ottiene uguagliando a zero il complesso dei termini di primo grado.
Per esempio la curva di equazione x3 + y3 - x = 0 passa per l'origine ed ha ivi per tangente la retta di equazione x =0.
Tangenti per un punto ad una circonferenza
Esempi
1)-Scrivere le equazioni delle tangenti al cerchio x2 + y2 - 4x + 4y - 2 = 0 uscenti dal punto P(4, 2).
Primo procedimento
Si scrive l'equazione di una retta generica passante per P(4, 2):
y - 2 = m(x - 4)
e s'impone che le due intersezioni della retta con il cerchio coincidano, cioè le radici dell'equazione di secondo grado in x, o y, risolvente del sistema
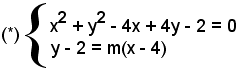
siano reali e coincidenti.
Affinchè l'equazione
(1 + m2)x2 - 4(2m2 - 2m + 1)x + 16m2 - 32m + 10 = 0,
ottenuta sostituendo nella prima equazione del sistema (*) il valore della y ricavato dalla seconda, abbia radici reali e coincidenti occorre che il discriminante sia uguale a zero, cioè:
Δ = 4(2m2 - 2m + 1)2 - (1 + m2)(16m2 - 32m + 10) = 0.
Sviluppando e ordinando, si ha:
3m2 + 8m - 3 = 0,
da cui
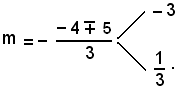

Le equazioni delle tangenti al cerchio dal punto P(4, 2) sono:
cioè
3x + y - 14 = 0 e x - 3y + 2 = 0.
Ricordando che un punto P(x0, y0) è esterno, appartiene o è interno al cerchio (x - α)2 + (y - β)2 = r2, a seconda che la sua distanza dal centro sia rispettivamente maggiore, uguale o minore del raggio.
Analiticamente ciò viene espresso dalla relazione:
Pertanto, si può verificare che il punto P(4, 2) è esterno al cerchio.
Infatti, la distanza di P(4, 2) dal centro C(2, -2) è:
ed essendo il raggio
risulta
I punti di contatto delle rette tangenti con il cerchio hanno coordinate rispettivamente A(1, 1) e B(-5, 1).
Secondo procedimento
Per scrivere le equazioni delle tangenti al cerchio x2 + y2 - 4x + 4y - 2 = 0 uscenti dal punto P(4, 2), si considera una generica retta uscente dal punto P(4, 2), la cui equazione è:
y - 2 = m(x - 4)
e s'impone che abbia distanza dal centro C(2, -2) di un segmento uguale al raggio
del cerchio.
Per la nota formula della distanza, si trova la condizione:
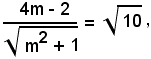
elevando al quadrato ed ordinando, si ha
3m2 + 8m - 3 = 0,
da cui
Sostituendo ad m tali valori nell'equazione y - 2 = m(x - 4), si hanno le equazioni delle tangenti al cerchio uscenti dal punto P(4, 2), cioè le equazioni:
3x + y - 14 = 0 e x - 3y + 2 = 0.
I due procedimenti esposti possono essere utilizzati per determinare la tangente al cerchio in un suo punto, per quanto sia preferibile, par la rapidità di calcolo, la formula (7):
(7) xx0 + yy0 - α(x + x0) - β(y - y0) + γ = 0.
2)-Trovare la tangente alla circonferenza x2 + y2 - 2x - 4y + 4 = 0 nel suo punto P(1, 3).
Primo procedimento
Si scrive l'equazione di una retta generica passante per P(1, 3) e si cercano le intersezioni di questa con il cerchio, una è P, e s'impone che coincidano. l'equazione del fasci di rette di centro P è:
y - 3 = m(x -1);
le coordinate dei punti di intersezione si trovano risolvendo il sistema:
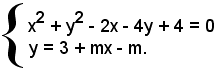
Queste coincidono se le radici dell'equazione risolvente:
(1 + m2)x2 - 2(m2 - m + 1)x + m2 - 2m + 1 = 0,
ottenuta sostituendo nella prima equazione del sistema il valore della y ricavato dalla seconda, abbia radici reali e coicidenti occorre che il discriminante sia uguale a zero, cioè:
Δ = (m2 - m + 1)2 - (1 + m2)(m2 - 2m + 1) = 0,
Sviluppando, ordinando e risolvendo, si ha:
m2 = 0,
da cui
m1 = m2 = 0.
Sostituendo tale valore nell'equazione y = 3 + mx - m, si ha l'equazione cercata: y = 3.
Secondo procedimento
Si scrive l'equazione di una generica retta per P(1, 3) e s'impone che abbia distanza dal centro C(1, 2) di un segmento uguale al raggio r =1.
L'equazione di una retta generica per P(1, 3) è:
y - 3 = m(x - 1),
ossia
mx - y - m + 3 = 0;
la distanza della retta dal centro C(1, 2) dev'essere uguale a 1, quindi:
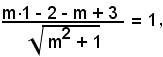
da cui
ossia
m = 0.
L'equazione della retta tangente al cerchio nel punto P(1, 3) è y - 3 = 0.

3)-Trovare le equazioni delle tangenti al cerchio x2 + y2 - 2x - 4y + 1 = 0 uscenti dal punto P(1, 1), interno ad esso.
Infatti, si verifica che il punto P è interno al cerchio: sostituendo nell'equazione del cerchio ad x ed y i valori 1 e 1, ascissa e ordinata di P, si ha
1 + 1 - 2 - 4 + 1 = -3 < 0,
cioè la distanza di P da C è minore di r.
Tale risultato si riscontra applicando i due procedimenti svolti negli esempi precedenti.

Riassumendo i risultati dei tre esempi, si può affermare che:
-il problema di condurre da un punto dato le tangenti ad un cerchio dato, ammette due soluzioni reali e distinte quando il punto è esterno al cerchio, due soluzioni reali e coincidenti quando il punto sta sul cerchio, due soluzioni immaginarie e coniugate quando il punto è interno al cerchio.
Potenza di un punto rispetto a un cerchio
Siano dati il cerchio di equazione x2 + y2 - 2αx - 2βy + γ = 0 ed il punto P(x0, y0).
ossia
(8) p = (x0 - α)2 + (y0 - β)2 - r2,
essendo
Si può dunque affermare che:
-la potenza del punto P(x0, y0) rispetto al cerchio di equazione x2 + y2 - 2αx - 2βy + γ = 0 è uguale, in valore e segno, al primo membro dell'equazione della circonferenza scritta in forma normale, quando al posto delle coordinate correnti x ed y, si sostituiscono le coordinate del punto.
I punti esterni al cerchio hanno potenza positiva, mentre quelli interni hanno potenza negativa.
cioè
da cui
se P(x0, y0) è interno al cerchio x2 + y2 - 2αx - 2βy + γ = 0, si ha:
cioè
da cui
i punti appartenenti al cerchio hanno potenza nulla; il cerchio dunque è il luogo geometrico dei punti del piano aventi rispetto ad esso potenza nulla.
Esempio - Determinare il valore della potenza del punto P(1, 2) rispetto al cerchio di equazione x2 + y2 - 4x + 2y + 1 = 0.
Applicando la (8), si ha:
ll punto P è esterno al cerchio, essendo la sua potenza positiva.
Infatti, il punto P ha dal centro distanza maggiore del raggio.
Essendo:
si ha:
Si verifica come il valore 6, potenza di P(1, 2) rispetto al cerchio dato, rappresenti il prodotto delle distanze di P dalle intersezioni con il cerchio di una retta uscente da P. Allo scopo, si considera la retta uscente da P di coefficiente angolare 3 e si determinano le coordinate dei punti A e B, intersezioni di tale retta con il cerchio dato.
Risolvendo il sistema:
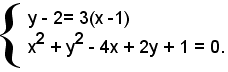
si trovano le coordinate di A , 0 E - 1, e le coordinate di B, 2/5 E 1/5.
Il prodotto della distanze di P da A e B è dato da:
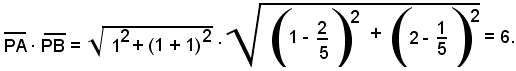
Dopo aver ripetuto il calcolo per la retta che esce da P, che è parallela all'asse y, si ha che i punti di contatto T e T' delle tangenti, come si e visto, condotte da P al cerchio hanno coordinate:
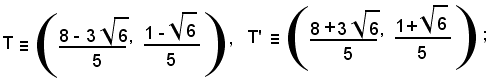
per cui
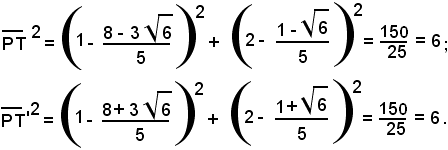
Si è così verificato che:
Asse radicale di due cerchi - Fasci di cerchi - Asse centrale
Siano date due circonferenze di equazioni:
x2 + y2 - 2αx - 2βy + γ = 0,
x2 + y2 - 2α'x - 2β'y + γ' = 0.
Le coordinate dei punti di intersezione sono date dalla soluzione del sistema:
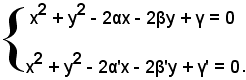
Tale sistema è di quarto grado ed è equivalente al sistema di secondo grado seguente:
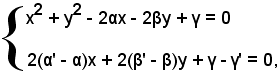
le cui soluzioni forniscono le coordinate dei due punti reali A e B.
Si ricordi che il grado di un sistema di equazioni algebriche è dato dal prodotto dei gradi delle equazioni componenti.
La retta di equazione:
(9) 2(α' - α)x + 2(β' - β)y + γ - γ' = 0,
ottenuta sottraendo le equazioni dei due cerchi dati, si chiama asse radicale, evidenziato in rosso nella figura seguente.
ottenuta sottraendo le equazioni dei due cerchi dati, si chiama asse radicale, evidenziato in rosso nella figura seguente.

L'asse radicale è la retta AB, che congiunge i due punti reali A e B in cui si intersecano i cerchi dati.
Tale retta rappresenta il luogo geometrico dei punti che hanno uguale potenza rispetti ai cerchi stessi.
Infatti, se si indica con P un punto generico del piano di coordinate x ed y, la sua potenza rispetto al primo cerchio è uguale al primo membro della sua equazione; la sua potenza rispetto al secondo cerchio è uguale al primo membro della seconda equazione; affinchè P abbia la stessa potenza rispetto ai due cerchi, dev'essere:
x2 + y2 - 2α'x - 2β'y + γ' = x2 + y2 - 2αx - 2βy + γ,
da cui trasportando tutto nel secondo membro, si ha l'equazione dell'asse radicale.
2(α' - α)x + 2(β' - β)y + γ - γ' = 0.
Se i due cerchi sono secanti, l'asse radicale è dato dalla retta AB, che congiunge i punti A e B; se i due cerchi sono tangenti, l'asse radicale è la tangente comune ai due cerchi; se i due cerchi sono esterni, l'asse radicale è esterno ad entrambi i cerchi.
Costruzione dell'asse radicale di due cerchi esterni
Per costruire l'asse radicale di due cerchi esterni α e β, si considera un terzo cerchio γ secante entrambi; si determina l'asse radicale dei cerchi α e γ e l'asse radicale dei cerchi β e γ. Essi s'incontrano in un punto M, la perpendicolare per M alla retta congiungente i centri dei due cerchi dati α e β, asse centrale, dà l'asse radicale richiesto.

Gli infiniti cerchi passanti per i punti A e B, punti di intersezione di due cerchi dati, costituiscono il fascio di cerchi. L'equazione del fascio di cerchi si ottiene facendo una combinazione lineare dei cerchi dati, cioè sommando la prima equazione con la seconda moltiplicata per un parametro λ.
Essa è del tipo:
x2 + y2 - 2αx - 2βy + γ + λ(x2 + y2 - 2α'x - 2β'y + γ') = 0,
ossia
da cui
La retta congiungente i centri C(α, β) C'(α', β') si chiama asse centrale. La sua equazione è:
ossia, sviluppando e riducendo,
(11) (β' - β)x - (α' - α)y + α'β - αβ' = 0.
Si rileva facilmente come l'asse centrale sia perpendicolare all'asse radicale.
Infatti, è soddisfatta la condizione di perpendicolarità delle due rette:
2(β' - β)(α' - α) - 2(α' - α)(β' - β) = 0.
Nota bene
Si vedrà in seguito che:
-viceversa, data l'equazione di un fascio di cerchi, le equazioni dei due cerchi fondamentali si ottengono ponendo λ = 0 e λ = ∞ nell'equazione (10).
Per λ = - 1, la (10) fornisce l'equazione dell'asse radicale, poichè per ogni valore di λ la (10) dà un cerchio passante per i punti dase del fascio A e B, L'asse radicale può considerarsi come un cerchio limite del fascio, che ha raggio infinito.
Esempi
1)-Scrivere l'equazione dell'asse radicale dei cerchi:
α) x2 + y2 - 2x - 2y - 2 = 0,
β) x2 + y2 - 8x + 4y + 4 = 0;
verificare inoltre che esso è il luogo dei punti che hanno uguale potenza rispetto ai cerchi stessi.

Sottraendo le equazioni dei due cerchi α e β, si ha l'equazione dell'asse radicale; essa è:
Per verificare che ogni punto dell'asse radicale ha la stessa potenza rispetto ai cerchi α e β, si indicano con x ed y le coordinate di un generico punto P. La potenza del punto P rispetto al cerchio di equazione α è uguale a x2 + y2 - 2x - 2y - 2; la potenza del punto P rispetto al cerchio di equazione β è uguale a x2 + y2 - 8x + 4y + 4.
Affinchè il punto P abbia la stessa potenza rispetto ai due cerchi occorre che sia:
x2 + y2 - 2x - 2y - 2 = x2 + y2 - 8x + 4y + 4.
Trasportando tutto al primo membro e semplifIcando, si ottiene:
x - y - 1 = 0,
condizione di appartenenza del punto P(x, y) alla retta x - y - 1 = 0.
Quindi, tutti e soli i punti dell'asse radicale hanno uguale potenza rispetto ai cerchi α e β.
L'equazione dell'asse centrale è:
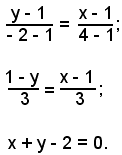
Si rileva che l'asse centrale è perpendicolare all'asse radicale, in quanto è soddisfatta la condizione di perpendicolarità.
2)-Trovare il cerchio che passa per le intersezioni dei cerchi x2 + y2 - 1 = 0 e x2 + y2 + 2x = 0 e per il punto P.
Il problema ammette una sola soluzione, in quanto si deve determinare un cerchio passante per tre punti, cioè per i due punti comuni ai cerchi dati e per il punto P.
Gli infiniti cerchi passanti per i punti comuni dei cerchi dati hanno equazione:
(1 + λ)(x2 + y2) - 1 + 2λx = 0,
ottenuta facendo una combinazione lineare delle equazioni dei due cerchi, cioè sommando la prima con la seconda equazione moltiplicata per il parametro λ.
Dividendo l'equazione del fascio per 1 + λ, si ottiene l'equazione del fascio in forma normale:
Un cerchio del fascio passa per il punto P(3, 2), se le coordinate di P soddisfano tale equazione, cioè se si verifica:
Risolvendo rispetto a λ, si ha:
Sostituendo tale valore in
si ottiene l'equazione del cerchio richiesto:
3)-Scrivere l'equazione del cerchio passante per i punti comuni al cerchio x2 + y2 - 4x + 2y + 1 = 0 e x2 + y2 + 2x = 0 e alla retta 3x - y + 5 = 0 e per l'origine della coordinate.
Si ricordi che si definiscono "fascio di cerchi" gli infiniti cerchi passanti per due punti.
Quindi, per i punti comuni al cerchio e alla retta passano infiniti cerchi, il cui asse radicale è la stessa retta.
-viceversa, data l'equazione di un fascio di cerchi, le equazioni dei due cerchi fondamentali si ottengono ponendo λ = 0 e λ = ∞ nell'equazione (10).
Per λ = -1, la (10) fornisce l'equazione dell'asse radicale, poichè per ogni valore di λ la (10) dà un cerchio passante per i punti dase del fascio A e B. L'asse radicale può considerarsi come un cerchio limite del fascio, che ha raggio infinito.
L'equazione del fascio si ottiene facendo la combinazione lineare delle equazioni date, cioè sommando la prima equazione con la seconda moltiplicata per il parametro λ. Essa è:
ossia
x2 + y2 - (4 - 3λ)x + (2 - λ)y + 1 + 5λ = 0.
Per trovare il cerchio del fascio che passa per l'origine, basta uguagliare a zero il termine noto, cioè
1 + 5λ = 0,
da cui λ = -7/5; sostituendo tale valore nell'equazione del fascio, si trova l'equazione del cerchio richiesto:
Dato il fascio di cerchi x2 + y2 - 2x + λ(x2 + y2 - 3y) = 0, determinare:
a)-i cerchi fondamentali:
b)-i cerchi del fascio che hanno raggio 1.
a)-I cerchi fondamentali del fascio si ottengono per i valori particolari del parametro λ: per λ = 0 e λ = ∞. Per λ = 0, si ha il cerchio x2 + y2 - 2x = 0.
Si divide ora l'equazione del fascio per λ e si ricordi che una frazione con denominatore infinito è uguale a zero.
Per λ = ∞, si ha:
ossia
x2 + y2 - 3y = 0.
b)-Il centro del generico cerchio del fascio:
x2 + y2 - 2x + λ(x2 + y2 - 3y) = 0,
ossia ordinando e riducendo tale equazione in forma normale
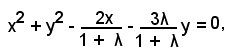
ha coordinate
Ricordando che:
si ha
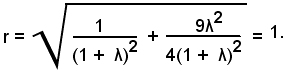
Elevando al quadrato ambo i membri e riducendo, si ha:
5λ2+ λ= 0,
da cui
Sostituendo tali valori nell'equazione del fascio, si hanno le equazioni dei due cerchi:
x2 + y2 - 2x = 0.
Polare di un punto rispetto a un cerchio
Si riprende l'esempio visto per le tangenti a un cerchio in un punto, per trovare una soluzione più semplice.
In tale esempio si chiedeva di scrivere le equazioni delle tangenti al cerchio x2 + y2 - 4x + 4y - 2 = 0 uscenti dal punto P(4, 2).
Supponendo di aver risolto il problema, si indicano con a e b le tangenti al cerchio uscenti da P e con T e T' i rispettivi punti di contatto, come in figura.

Quindi, le tangenti a e b sono le rette congiungenti il punto P con i punti T e T'.
I punti T e T' sono i punti di intersezione della retta TT' con il cerchio.
La retta TT', che si indica con p, si chiama polare del punto P rispetto al cerchio e P polo.
La sua equazione è:
x + 2y - 3 = 0,
ottenuta applicando la formula di sdoppiamento, cioè sostituendo nell'equazione del cerchio dato 4x ad x2, 2y ad y2, (x+4)/2 ad x, (y + 2)/2 ad y.
La retta TT' coincide con p, polare di P rispetto al cerchio la si può definire così:
-retta congiungente i punti di contatto delle tangenti condotte dal punto al cerchio.
Le coordinate T e T' sono date dalla soluzione del sistema:
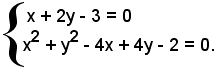
Esse sono T(1, 1) e T'(5, -1).
Le due tangenti a e b, rette congiungenti rispettivamente i punti P, T e P, T' hanno equazioni:
ossia
a) x - 3y + 2 = 0 e 3x + y - 14 = 0.
Poichè la retta TT', coincidente con p, si è ottenuta applicando l'equazione (7) con la formula di sdoppiamento, si può affermare che l'equazione della polare di un punto P rispetto ad un cerchio coincide con l'equazione della tangente al cerchio, se P appartiene ad esso, cioè:
-la polare di un punto del cerchio è la tangente ad esso in quel punto.
In conclusione:
-se il punto P è esterno al cerchio, la polare è secante ad esso ed è la retta congiungente i punti di contatto delle tangenti condotte dal punto al cerchio;
-se P è un punto del cerchio, la polare coincide con la tangente in P;
-se P è un punto interno al cerchio, la polare è esterna.
Si osservi come la polare di P rispetto al cerchio sia perpendicolare alla retta CP.
Infatti, la polare di P rispetto al cerchio dato ha coefficiente angolare m = -1/2 e la retta CP ha coefficiente angolare m' = (2 + 2)/(4 - 2) = 2.
Si ricorda che la condizione di perpendicolarità fra due rette è che il prodotto dei coefficienti è uguale a -1.
Si osserva ancora come il prodotto delle distanze del polo e della polare dal centro del cerchio sia uguale al quadrato del raggio.
Infatti, la distanza
e la distanza della retta TT' da C è:
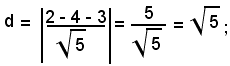
dunque:
Mediante le proprietà enunciate si può costruire la polare di un punto rispetto al cerchio.
Se il punto P è esterno al cerchio, si conducono le tangenti da P al cerchio, la retta congiungente i punti di contatto è la polare di P richiesta.
Se P appartiene al cerchio la polare è la tangente in P ad esso.
Se P è interno al cerchio, la sua polare si costruisce nel modo seguente, come in figura.

Per P si conducono la perpendicolare fino ad incontrare in M il cerchio, la tangente in M ad esso incontra la CP in R, la perpendicolare per R alla CP è la polare del polo P.
Si osservi che tale costruzione è fatta in base alla proprietà enunciata per i triangoli rettangoli.
Infatti, dal triangolo rettangolo CMR, per il Teorema di Euclide, si ha:
ossia
In generale, l'equazione della polare nel punto P(x0, y0) rispetto al cerchio
x2 + y2 - 2αx - 2 βy + γ = 0,
applicando la formula di sdoppiamento, è:
(12) xx0 + yy0 - α(x + x0) - β(y + y0) + γ = 0.
Si può concludere che:
la (12) rappresenta l'equazione della tangente in P(x0, y0) al cerchio x2 + y2 - 2αx - 2βy + γ = 0, se il punto P appartiene al cerchio; è invece l'equazione della polare di P rispetto al cerchio, se P non appartiene al cerchio, cioè la (12), in ogni caso, rappresenta l'equazione della retta congiungente i punti di contatto delle tangenti condotte dal punto al cerchio.