MIKY & GENNY
COORDINATE CARTESIANE NEL PIANO ---> INDICE
Si
fissino nel piano due rette orientate, passanti per lo
stesso punto O, la prima orizzontale, orientata da sinistra
verso
destra, la seconda perpendicolare in O alla prima, orientata dal basso
verso l'alto.
Si assegni su entrambe le rette uno stesso segmento u, unità di misura, ed i punti U' e U'', presi rispettivamente sulla prima e sulla seconda delle rette indicate, tali che OU' = OU'' = u.
U' e U'' rappresentano le proiezioni ortogonali sulle stesse, del punto unità U, preso fuori dalle rette.
Le due rette costituiscono una coppia di assi coordinati cartesiani, la prima si chiama asse delle ascisse o asse x, la seconda asse delle ordinate o asse y, il punto O origine delle coordinate ed i punti U e U' punti unità.
Il punto O divide la retta orizzontale in due semirette di origine O: la semiretta che contiene il punto U' si chiama semiasse positivo x, l'altra semiasse negativo x.
Il punto O divide anche la retta verticale semirette di origine O: la semiretta che contiene il punto U'' si chiama semiasse positivo y, l'altra semiasse negativo y.
Sia P un punto del piano e da esso si conducano le rette PN e PM, rispettivamente parallele agli assi x ed y.
Il numero a, razionale o irrazionale, positivo o negativo, misura del segmento PN o del segmento OM, secondo l'unità prefissata u, si chiama ascissa del punto P; analogamente, il numero b, razionale o irrazionale, positivo o negativo, misura del segmento PM o del segmento ON, secondo l'unità prefissata u, si chiama ordinata del punto P. Quindi le coordinate di P sono a e b e si suole scrivere P (a, b), convenendo di scrivere prima l'ascissa e poi l'ordinata.
In tal modo ad un punto qualunque P del piano viene associato una coppia di numeri reali relativi.
Viceversa, dato un sistema di coordinate e una coppia ordinata di numeri relativi (a, b), si determina sull'asse x il punto M, tale che OM/OU' = a e sull'asse y il punto N, tale che ON/OU'' = b. Le parallele per M all'asse y, e per N all'asse x, s'incontrano nel punto P di coordinate a e b.

Si è stabilita così una corrispondenza biunivoca e continua, senza eccezioni, tra i punti del piano e le coppie di numeri reali relativi, tale che ad ogni coppia di numeri reali relativi corrisponde uno ed un solo punto del piano e viceversa.
Nota bene
La corrispondenza biunivoca è anche continua, perchè ad una piccolissima variazione delle coordinate, corrisponde uno spostamento piccolissimo del punto.
I due assi ortogonali x e y dividono il piano in quattro quadranti o regioni, o angoli, che prendono il nome rispettivamente di I, II, III, IV quadrante.
Nella numerazione dei quadranti si comincia da quella limitata dai semiassi positivi e si prosegue secondo il senso positivo delle rotazioni, verso contrario al movimento delle lancette dell'orologio. L'ascissa a e l'ordinata b di P hanno, a seconda del quadrante in cui P giace, i segni indicati nella tabella seguente:
Le coordinate (a, b) del punto P danno dunque le misure delle distanze del punto P dai due assi prefissati.
Caratteristiche dei punti
-I punti dell'asse x hanno l'ordinata nulla;
-I punti dell'asse y hanno l'ascissa nulla.
Indicando con x ed y l'ascissa e l'ordinata di un punto del piano, l'asse x e l'asse y si possono rappresentare con le rispettive equazioni:
-asse x: y =0;
-asse y: x =0.
L'origine O ha coordinate (0,0);
I punti U e U' hanno rispettivamente coordinate (1, 0), (0,1).
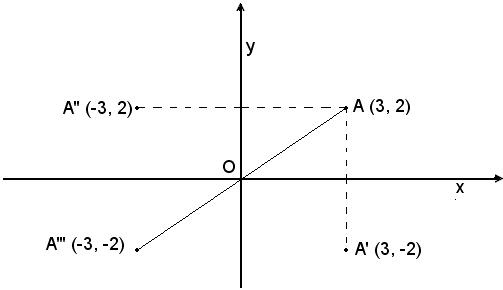
Due punti simmetrici rispetto all'asse x hanno ascisse uguali ed ordinate opposte.
Esempio:
A (3, 2) e A' (3, -2).
Due punti simmetrici rispetto all'asse y hanno ascisse opposte ed ordinate uguali.
Esempio:
A (3, 2) e A'' (-3, 2).
Due punti simmetrici rispetto all'origine O hanno ascisse ed ordinate opposte.
Esempio:
Nota bene
Si ricorda che: due punti A e B si dicono simmetrici rispetto ad una retta quando questa è l'asse del segmento AB; si dicono invece simmetrici rispetto ad un punto M, quando M è il punto medio del segmento AB.
Punto medio di un segmento
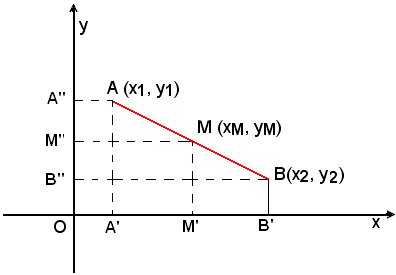
Dati i punti A (x1, y1) e B(x2, y2) si vogliono determinare le coordinate del punto medio del segmento AB.
Siano A', M', B' e A'', M'', B'' le proiezioni ortogonali dei punti A, M, B, rispettivamente sull'asse x e sull'asse y.
Per il teorema di Talete, essendo M punto medio di AB, M' e M'' saranno rispettivamente i punti medi dei segmenti A'B' e A''B''. Si tratta allora di determinare le coordinate del punto medio di un segmento appartenente ad una retta orientata, come già è stato visto, quindi si ha:
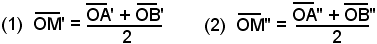
e, ricordando che è l'ascissa di M,
è l'ascissa di M,  è l'ascissa di A,
è l'ascissa di A,  è l'acissa di B, la (1) si trasforma
in:
è l'acissa di B, la (1) si trasforma
in:
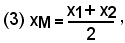
cioè l'ascissa del punto medio di due punti è uguale alla semisomma delle ascisse dei due punti.
Analogamente, essendo l'ordinata di M,
l'ordinata di M,  l'ordinata di A,
l'ordinata di A,  l'ordinata di B, la (2) si
trasforma in:
l'ordinata di B, la (2) si
trasforma in:
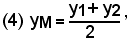
cioè l'ordinata del punto medio di due punti è uguale alla semisomma delle ordinate dei due punti.
In conclusione:
-le coordinate del punto medio di un segmento sono uguali alla semisomma delle coordinate omonime degli estremi.
Esempio:
le coordinate del punto medio M del segmento di estremi A (1, 1) e B (-3, 4) sono date da
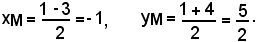
Distanza di due punti.
Siano M (x1, y1) e N (x2, y2) due punti del piano, di cui si conoscano le coordinate. Si vuole determinare, in valore assoluto, la loro distanza:
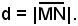
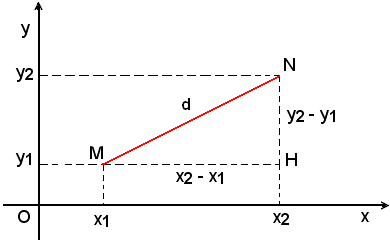
Applicando
il teorema di Pitagora al triangolo rettangolo MHN, ove H è
il
piede della perpendicolare abbassata da N sulla parallela per M
all'asse x, di cateti:

si ha
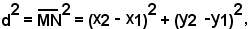
da cui estraendo la radice quadrata, si ottiene la formula fondamentale:
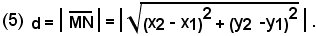
La distanza di due punti, in valore assoluto, è data dalla somma dei quadrati delle differenze fra le coordinate omonime dei due punti.
Nota bene
Nel caso che la retta MN sia orientata, d sarà positivo o negativo a seconda che il segmento MN sia equiverso o contraverso alla retta.
In particolare se il punto M coincide con O, la (5) si trasforma in:
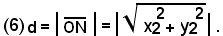
La distanza di un punto dall'origine è data, in valore assoluto, dalla radice quadrata della somma dei quadrati delle coordinate del punto.
Esempi
1)-La distanza dei punti M (-5, 3) e N (7, 3) è data da:
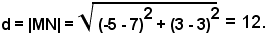
2)-La distanza di P (3, -4) dall'origine è data da:
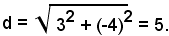
Si assegni su entrambe le rette uno stesso segmento u, unità di misura, ed i punti U' e U'', presi rispettivamente sulla prima e sulla seconda delle rette indicate, tali che OU' = OU'' = u.
U' e U'' rappresentano le proiezioni ortogonali sulle stesse, del punto unità U, preso fuori dalle rette.
Le due rette costituiscono una coppia di assi coordinati cartesiani, la prima si chiama asse delle ascisse o asse x, la seconda asse delle ordinate o asse y, il punto O origine delle coordinate ed i punti U e U' punti unità.
Il punto O divide la retta orizzontale in due semirette di origine O: la semiretta che contiene il punto U' si chiama semiasse positivo x, l'altra semiasse negativo x.
Il punto O divide anche la retta verticale semirette di origine O: la semiretta che contiene il punto U'' si chiama semiasse positivo y, l'altra semiasse negativo y.
Sia P un punto del piano e da esso si conducano le rette PN e PM, rispettivamente parallele agli assi x ed y.
Il numero a, razionale o irrazionale, positivo o negativo, misura del segmento PN o del segmento OM, secondo l'unità prefissata u, si chiama ascissa del punto P; analogamente, il numero b, razionale o irrazionale, positivo o negativo, misura del segmento PM o del segmento ON, secondo l'unità prefissata u, si chiama ordinata del punto P. Quindi le coordinate di P sono a e b e si suole scrivere P (a, b), convenendo di scrivere prima l'ascissa e poi l'ordinata.
In tal modo ad un punto qualunque P del piano viene associato una coppia di numeri reali relativi.
Viceversa, dato un sistema di coordinate e una coppia ordinata di numeri relativi (a, b), si determina sull'asse x il punto M, tale che OM/OU' = a e sull'asse y il punto N, tale che ON/OU'' = b. Le parallele per M all'asse y, e per N all'asse x, s'incontrano nel punto P di coordinate a e b.

Si è stabilita così una corrispondenza biunivoca e continua, senza eccezioni, tra i punti del piano e le coppie di numeri reali relativi, tale che ad ogni coppia di numeri reali relativi corrisponde uno ed un solo punto del piano e viceversa.
Nota bene
La corrispondenza biunivoca è anche continua, perchè ad una piccolissima variazione delle coordinate, corrisponde uno spostamento piccolissimo del punto.
I due assi ortogonali x e y dividono il piano in quattro quadranti o regioni, o angoli, che prendono il nome rispettivamente di I, II, III, IV quadrante.
Nella numerazione dei quadranti si comincia da quella limitata dai semiassi positivi e si prosegue secondo il senso positivo delle rotazioni, verso contrario al movimento delle lancette dell'orologio. L'ascissa a e l'ordinata b di P hanno, a seconda del quadrante in cui P giace, i segni indicati nella tabella seguente:
| Quadrante | Ascissa a | Ordinata b |
| I | + | + |
| II | - | + |
| III | - | - |
| IV | + | - |
Le coordinate (a, b) del punto P danno dunque le misure delle distanze del punto P dai due assi prefissati.
Caratteristiche dei punti
-I punti dell'asse x hanno l'ordinata nulla;
-I punti dell'asse y hanno l'ascissa nulla.
Indicando con x ed y l'ascissa e l'ordinata di un punto del piano, l'asse x e l'asse y si possono rappresentare con le rispettive equazioni:
-asse x: y =0;
-asse y: x =0.
L'origine O ha coordinate (0,0);
I punti U e U' hanno rispettivamente coordinate (1, 0), (0,1).
Due punti simmetrici rispetto all'asse x hanno ascisse uguali ed ordinate opposte.
Esempio:
A (3, 2) e A' (3, -2).
Due punti simmetrici rispetto all'asse y hanno ascisse opposte ed ordinate uguali.
Esempio:
A (3, 2) e A'' (-3, 2).
Due punti simmetrici rispetto all'origine O hanno ascisse ed ordinate opposte.
Esempio:
A
(3, 2) e A''' (-3, -2).

Nota bene
Si ricorda che: due punti A e B si dicono simmetrici rispetto ad una retta quando questa è l'asse del segmento AB; si dicono invece simmetrici rispetto ad un punto M, quando M è il punto medio del segmento AB.
Punto medio di un segmento
Dati i punti A (x1, y1) e B(x2, y2) si vogliono determinare le coordinate del punto medio del segmento AB.
Siano A', M', B' e A'', M'', B'' le proiezioni ortogonali dei punti A, M, B, rispettivamente sull'asse x e sull'asse y.
Per il teorema di Talete, essendo M punto medio di AB, M' e M'' saranno rispettivamente i punti medi dei segmenti A'B' e A''B''. Si tratta allora di determinare le coordinate del punto medio di un segmento appartenente ad una retta orientata, come già è stato visto, quindi si ha:

e, ricordando che
cioè l'ascissa del punto medio di due punti è uguale alla semisomma delle ascisse dei due punti.
Analogamente, essendo
cioè l'ordinata del punto medio di due punti è uguale alla semisomma delle ordinate dei due punti.
In conclusione:
-le coordinate del punto medio di un segmento sono uguali alla semisomma delle coordinate omonime degli estremi.
Esempio:
le coordinate del punto medio M del segmento di estremi A (1, 1) e B (-3, 4) sono date da
Distanza di due punti.
Siano M (x1, y1) e N (x2, y2) due punti del piano, di cui si conoscano le coordinate. Si vuole determinare, in valore assoluto, la loro distanza:

si ha
da cui estraendo la radice quadrata, si ottiene la formula fondamentale:
La distanza di due punti, in valore assoluto, è data dalla somma dei quadrati delle differenze fra le coordinate omonime dei due punti.
Nota bene
Nel caso che la retta MN sia orientata, d sarà positivo o negativo a seconda che il segmento MN sia equiverso o contraverso alla retta.
In particolare se il punto M coincide con O, la (5) si trasforma in:
La distanza di un punto dall'origine è data, in valore assoluto, dalla radice quadrata della somma dei quadrati delle coordinate del punto.
Esempi
1)-La distanza dei punti M (-5, 3) e N (7, 3) è data da:
2)-La distanza di P (3, -4) dall'origine è data da: