MIKY & GENNY
DISCUSSIONE DELLE EQUAZIONI PARAMETRICHE DI PRIMO GRADO ---> INDICE
Prima
di discutere le equazioni parametriche di primo grado
mediante l'uso della retta, si dà la seguente definizione:
-si chiama disequazione o inequazione una relazione del tipo:
(1) A > B, (1') A < B,
dove A e B sono due espressioni, funzioni, una o più volte variabili. Risolvere una disequazione significa determinare le eventuali soluzioni, cioè quei valori delle variabili per i quali la (1) o la (1') è verificata.
Per risolvere le disequazioni:
ax + b > 0 e ax + b < 0,
con a≠0, si associa ad esse la retta di equazione
y = ax + b.
Il problema è ricondotto a determinare per quali valori di x l'ordinata y della retta è positiva o negativa.
Esempi
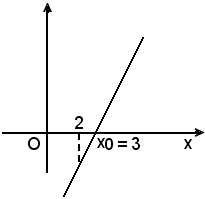
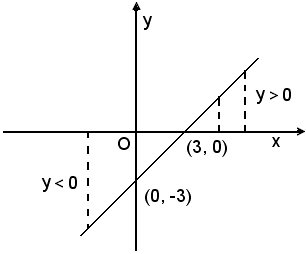
1)-Risolvere le disequazioni:
x - 3 > 0 e x - 3 < 0.
Si associa ad esse la retta di equazione y = x - 3. Poichè il coefficiente di x è positivo, a = 1, la retta forma con l'asse x un angolo acuto, essendo il coefficiente angolare m = 1 e taglia l'asse y nel punto di coordinate (0, 3) e l'asse x nel punto x = 3, radice dell'equazione data.
I punti della retta aventi ordinate positive sono tutti e soltanto quelli le cui ascisse sono maggiori di 3.
Quindi, la disequazione x - 3 > 0 è soddisfatta per i valori di x > 3.
I punti della retta aventi ordinate negative sono solamente quelli le cui ascisse sono minori di 3.
Di conseguenza la disequazione x - 3 < 0 è soddisfatta per i valori di x < 3.
-si chiama disequazione o inequazione una relazione del tipo:
(1) A > B, (1') A < B,
dove A e B sono due espressioni, funzioni, una o più volte variabili. Risolvere una disequazione significa determinare le eventuali soluzioni, cioè quei valori delle variabili per i quali la (1) o la (1') è verificata.
Per risolvere le disequazioni:
ax + b > 0 e ax + b < 0,
con a≠0, si associa ad esse la retta di equazione
y = ax + b.
Il problema è ricondotto a determinare per quali valori di x l'ordinata y della retta è positiva o negativa.
Esempi
1)-Risolvere le disequazioni:
x - 3 > 0 e x - 3 < 0.
Si associa ad esse la retta di equazione y = x - 3. Poichè il coefficiente di x è positivo, a = 1, la retta forma con l'asse x un angolo acuto, essendo il coefficiente angolare m = 1 e taglia l'asse y nel punto di coordinate (0, 3) e l'asse x nel punto x = 3, radice dell'equazione data.
I punti della retta aventi ordinate positive sono tutti e soltanto quelli le cui ascisse sono maggiori di 3.
Quindi, la disequazione x - 3 > 0 è soddisfatta per i valori di x > 3.
I punti della retta aventi ordinate negative sono solamente quelli le cui ascisse sono minori di 3.
Di conseguenza la disequazione x - 3 < 0 è soddisfatta per i valori di x < 3.
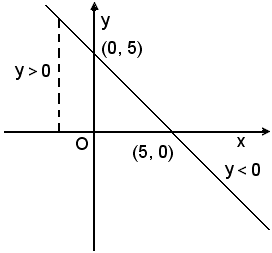
2)-Risolvere la disequazione:
-x + 5 > 0.
Si associa ad essa la retta di equazione y = -x + 5. Poichè il coefficiente di x è negativo, a = -1, la retta forma con l'asse x un angolo ottuso, essendo il coefficiente angolare m = a = -1 e taglia l'asse y nel punto di coordinate (0, 5) e l'asse x nel punto (5, 0). I punti della retta aventi ordinate positive sono tutti e soltanto quelli le cui ascisse sono minori di 5. Di conseguenza la disequazione -x + 5 > 0 è soddisfatta per i soli valori di x < 5.
Confronto delle radici di un'equazione di primo grado ad un'incognita con un numero reale dato
Sia data l'equazione ax + b = 0 con a≠0, la cui radice sia x0; si vuole confrontare tale radice con il numero reale α, cioè determinare la posizione α di rispetto a x0.
Si presentano i seguenti casi:
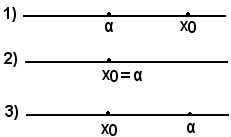
Per determinare le condizioni necessarie e sufficienti affinchè si verifichi uno dei casi suddetti, si pone f(x) = ax + b e si associa all'equazione f(x) = ax + b = 0 la retta:
y = af(x) = a2x + ab,
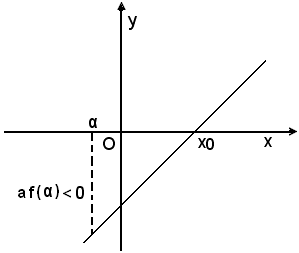
la quale presenta, essendo a2 > 0, il coefficiente angolare sempre positivo. Si indica con af(α) = a2α + ab l'ordinata del punto della retta di ascissa α.
Se af(α) < 0, α è alla sinistra di x0, ossia x0 > α.
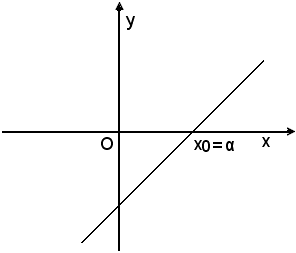
Se af(α) = 0, α coincide con x0, ossia x0 = α.
Se af(α) > 0, α è alla destra di x0, ossia x0 < α.
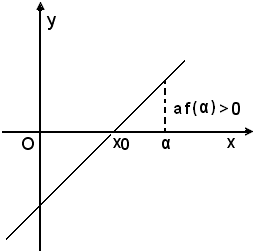
In conclusione:
-il numero α è maggiore, uguale o minore di x0 a seconda che af(α) sia rispettivamente maggiore, uguale o minore di 0.
Esempi
1)-Confrontare la radice dell'equazione x - 2 = 0 con il numero 3.
Si pone f(x) = x - 2 e si associa all'equazione data la retta y = af(x) = x - 2 per la quale m = 1 > 0 e q = -2.
Si calcola af(3) = 3 - 2 = 1 > 0; 3 è, dunque, alla destra di x0, ossia x0 < 3.
2)-Confrontare la radice dell'equazione x + 4 - k = 0 con il numero -1.
Si associa all'equazione f(x) = x + 4 - k = 0 la retta:
y = af(x) = x + 4 - k
per la quale m = 12 = 1 > 0.
Si osserva ora per quali valori del parametro k l'ordinata del punto, della retta di ascissa -1 è positiva, negativa o nulla.
Si calcola:
per la quale m = 12 = 1 > 0.
Si osserva ora per quali valori del parametro k l'ordinata del punto, della retta di ascissa -1 è positiva, negativa o nulla.
Si calcola:
af(-1) = -1 + 4 - k = 3 - k,
af(-1) ≥ 0 per k ≤ 3,
af(-1) < 0 per k > 3.
Per k < 3 af(-1) > 0 x0 < -1,
per k = 3 af(-1) = 0 x0 = -1,
per k > 3 af(-1) < 0 x0 > -1.
Confronto della radice di un'equazione di primo grado ad un'incognita con due numeri reali dati
Sia data l'equazione f(x) = ax + b = 0 con la coppia di numeri reali α e β, α > β, cioè si vuole determinare la posizione della radice x0 dell'equazione rispetto all'intervallo [α, β].
Si possono presentare i seguenti casi:
af(-1) ≥ 0 per k ≤ 3,
af(-1) < 0 per k > 3.
Per k < 3 af(-1) > 0 x0 < -1,
per k = 3 af(-1) = 0 x0 = -1,
per k > 3 af(-1) < 0 x0 > -1.
Confronto della radice di un'equazione di primo grado ad un'incognita con due numeri reali dati
Sia data l'equazione f(x) = ax + b = 0 con la coppia di numeri reali α e β, α > β, cioè si vuole determinare la posizione della radice x0 dell'equazione rispetto all'intervallo [α, β].
Si possono presentare i seguenti casi:

Per determinare le condizioni necessarie e sufficienti affinchè si verifichi uno dei casi elencati, si associa all'equazione f(x) = ax + b la retta:
y = af(x) = a2x + ab.
Si indicano con af(α) = a2α + ab e con af(β) = a2β + ab le ordinate dei punti della retta aventi, rispettivamente, ascisse α e β.
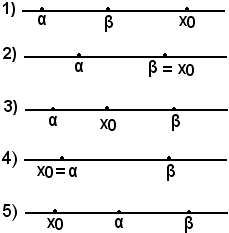
La radice x0 è esterna o interna all'intervallo [α, β] a seconda che af(α) e af(β) siano concordi o discordi; precisamente si verifica:
(1)-se af(β) < 0
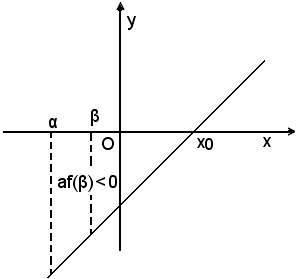
(2)-se af(β) = 0
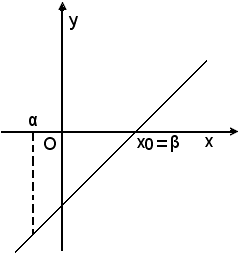
(3)-se f(α)·f(β) < 0
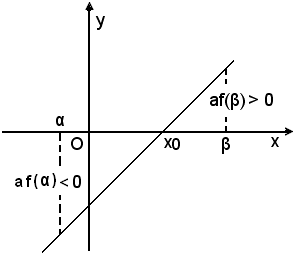
(4)-se af(α) = 0
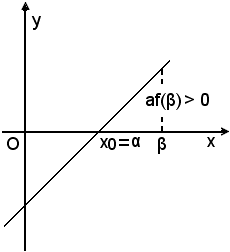
(5)-se af(α) > 0
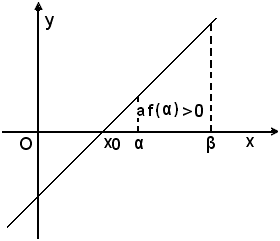
Esempi
1)-Confrontare le radici dell'equazione x - 3 = 0 con i numeri -1 e 1.
Si associa all'equazione f(x) = x - 3 = 0 la retta y = af(x) = x - 3 di coefficiente angolare m = 1 > 0.
Le ordinate dei punti della retta di ascisse rispettivamente -1 e 1 sono date da:
af(-1) = -1 - 3 = -4 < 0,
af(1) = 1 - 3 = -2 < 0;
si ha quindi
cioè
-1 < 1 < x0.
2)-Confrontare le radici dell'equazione 2x - k + 5 = 0 con i numeri 2 e 3.
2)-Confrontare le radici dell'equazione 2x - k + 5 = 0 con i numeri 2 e 3.
Si calcolano le ordinate dei punti della retta di ascissa rispettivamente 2 e 3.
af(2) = 8 - 2k + 10 = 18 - 2k = 2(9 - k)
af(3) = 12 - 2k + 10 = 22 - 2k = 2(11 - k)
af(2) > 0 per k < 9
af(2) = 0 per k = 9
af(2) < 0 per k > 9
af(3) > 0 per k < 11
af(3) = 0 per k = 11
af(3) < 0 per k > 11.
Si ordinano ora i valori del parametro k in ordine crescente, i quali rappresentano i capisaldi della discussione:
Per k < 9:
af(2) > 0 e x0 < 2 < 3.
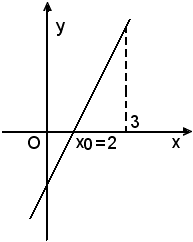
Per k = 9:
af(2) = 0 e x0 = 2.
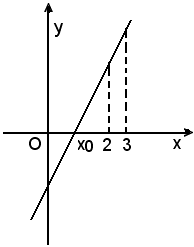
Per 9 < k < 11:
af(3) > 0, af(2) < 0 e 2 < x0 < 3.
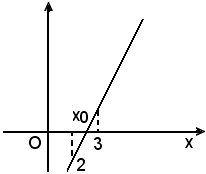
Per k > 11:
af(3) < 0 e 2 < 3 < x0.
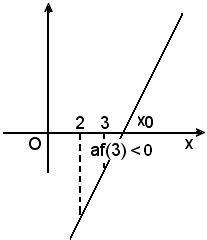
Per k = 11:
af(3) = 0 e x0= 3.