MIKY & GENNY
ELLISSE E COMPLEMENTI ---> INDICE
Definizione - Si chiama ellisse il luogo geometrico dei punti del piano per cui la somma delle distanze da due punti dati è costante.
I punti dati si chiamano fuochi dell'ellisse.
Si indicano con:
-F e F' i due fuochi,
-2c la lunghezza del segmento FF',
-2a la somma costante delle distanze di un punto generico P dell'ellisse dai punti F e F'.
Dalla definizione di ellisse, si ha:
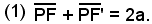
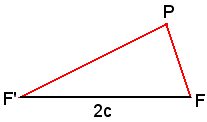
Poichè in un triangolo un lato è minore della somma degli altri due, nel triangolo FPF' dev'essere:

ossia
2c < 2a,
cioè
c < a.
Quest'ultima è la diseguaglianza fondamentale dell'ellisse.Per
trovare l'equazione cartesiana, si assume come asse x la retta
F'F e come asse y la perpendicolare nel punto medio O di F'F.
Poichè F'F = 2c, le coordinate dei fuochi sono F(c, 0) e F'(-c, 0).
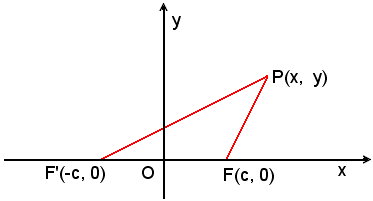
Indicando con x ed y le coordinate del generico punto P dell'ellisse, risulta:
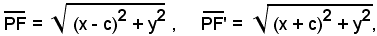
avendo applicato le formule dalla distanza di due punti.
Sostituendo tali valori nella (1), si ha:
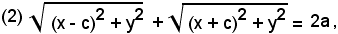
che per c < a rappresenta l'ellisse.
Si libera ora l'equazione irrazionale (2) dai radicali, portando il secondo radicale al secondo membro ed elevando al quadrato, si ha
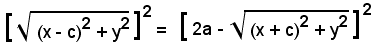
cioè
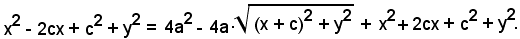
Isolando il radicale e riducendo, si ottiene:
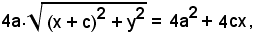
dividendo ambo i membri per 4, risulta
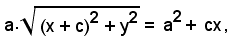
elevando al quadrato ambo i membri, si ha
a2 + [ x2 + 2cx + c2 + y2 ] = a4 + 2a2cx + c2x2
e semplificando, si trova
(3) (a2 - c2)x2 + a2y2 = a2(a2 - c2).
Essendo a > c, segue che a2 - c2 > 0 e quindi si può porre:
(4) a2 - c2 = b2
e sostituendo, la (3) diventa
b2x2+ a2y2 = a2b2,
dividendo ambo i membri per a2b2, infine si ottiene
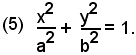
La (5) si chiama equazione canonica dell'ellisse.Dall'esame della (5) si possono conoscere le proprietà dell'ellisse.
a)-Proprietà di simmetria
L'ellisse di equazione (5) è simmetrica rispetto agli assi x, y è all'origine delle coordinate.
Si vuole dimostrare che se il punto P di coordinate x1 ed y1 appartiene all'ellisse, cioè le coordinate x1 ed y1 soddisfano l'equazione (5), ossia si verifica :
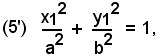
anche i punti P'(x1, -y1), P''(-x1, y1) e P'''(-x1, -y1), rispettivamente simmetrici del punto P rispetto all'asse x, all'asse y e all'origine, appartengono all'ellisse.
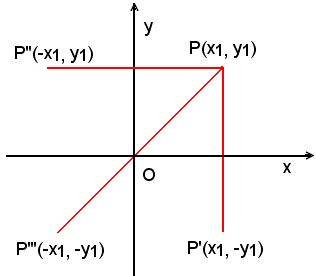
Infatti la (5') si può ovviamente porre sotto le forme equivalenti:
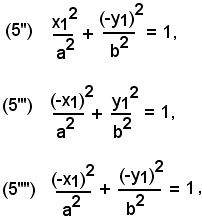
le quali esprimono rispettivamente l'appartenenza all'ellisse dei punti P'(x1, -y1), P''(-x1, y1) e P'''(-x1, -y1).
Nota bene
Generalità sulle curve
1)-Se nell'equazione di una curva algebrica la variabile y compare elevata soltanto a potenza pari, la curva è simmetrica rispetto all'asse x.
Infatti, se l'equazione della curva è soddisfatta dalle coordinate x1 e y1 di un punto P, essa è soddisfatta anche dalle coordinate x1, -y1 del punto P' rispetto all'asse x, in quanto elevando a potenza pari, il segno meno scompare. Così l'equazione x2y2 + x2 - y2 = 0, in cui la y compare soltanto in potenza di grado pari, rappresenta una curva algebrica simmetrica rispetto all'asse x.
Infatti, se la curva passa per P(x1, y1), cioè se x12y12 + x12 - y12 = 0, è anche x12(-y1)2 + x12 - (-y1)2 = 0, cioè la curva passa per P'(x1, -y1).
2)-Se nell'equazione di una curva algebrica la variabile x compare elevata soltanto a potenza pari, la curva è simmetrica rispetto all'asse y.
Così l'equazione x4 + y3 + x2 - y - 1 = 0, in cui la x compare soltanto in potenze di grado pari, rappresenta una curva algebrica simmetrica rispetto all'asse y.
Infatti, se la curva passa per P(x1, y1), cioè se x14 + y13 + x12 - y1 - 1 = 0, è anche (-x1)4 + y13 + (-x1)2 - y1 - 1 = 0, cioè la curva passa per P''(-x1, y1).
3)-Se nell'equazione di una curva algebrica tutti i termini sono di grado pari nella x e nella y, oppure i termini sono di grado dispari nella x e nella y, la curva è simmetrica rispetto all'origine.
Così l'equazione x2y2 + x2 - y2 = 0, che ha tutti i termini di grado pari nella x e nella y, rappresenta una curva algebrica simmetrica rispetto all'origine.
Infatti, se P(x1, y1) appartiene alla curva, cioè se x12y12 + x12 - y12 = 0, è anche
( -x1)2(-y1)2 + (-x1)2 - (-y1)2 = 0, cioè la curva passa per P'''(-x1, -y1).
Così dicasi per la curva di equazione x3 + y3 + x = 0.
b)-Vertici
Le intersezioni dell'ellisse con l'asse y si trovano risolvendo il sistema:
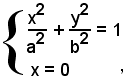
da cui
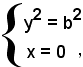
ossia
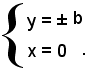
L'ellisse incontra l'asse y nei punti B(0, b) e B'(0, -b), che si chiamano vertici secondari; il segmento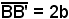 si chiama asse minore dell'ellisse, mentre il segmento
si chiama asse minore dell'ellisse, mentre il segmento 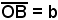 semiasse minore.
semiasse minore.
E' bene osservare che, essendo a > 0 e b > 0, dalla relazione (4) a2 - c2 = b2 si ricava a2 > b2, cioè a > b, quindi 2a > 2b, ossia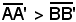 . Per tale motivo
. Per tale motivo 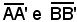 sono stati chiamati rispettivamente asse maggiore e asse minore.
sono stati chiamati rispettivamente asse maggiore e asse minore.
c)-Risolvendo l'equazione dell'ellisse rispetto alla variabile y, si ha:
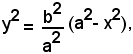
ossia
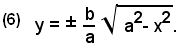
Affinchè la y abbia valori reali, occorre che:
a2- x2 ≥ 0,
ossia
|x| ≤ a,
cioè
-a ≤ x ≤ a.
Si ricordi che la condizione di realtà per un radicale di indice pari è che il radicando sia positivo o nullo. La radice di indice pari di una quantità negativa è immaginaria.
ossia
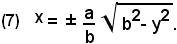
Affinchè la x abbia valori reali, occorre che:
b2- y2 ≥ 0,
ossia
|y| ≤ a,
cioè
-b ≤ y ≤ b.
Si hanno allora i punti reali della curva soltanto nell'interno della striscia di piano limitata dalle rette y = b e y = -b, rette tangenti all'ellisse, rispettivamente nei vertici B e B'.La parte reale dell'ellisse risulta così tutta interna al rettangolo avente per lati le rette x = ± a e
y = ± b. La curva ha l'andamento indicato nella figura seguente.
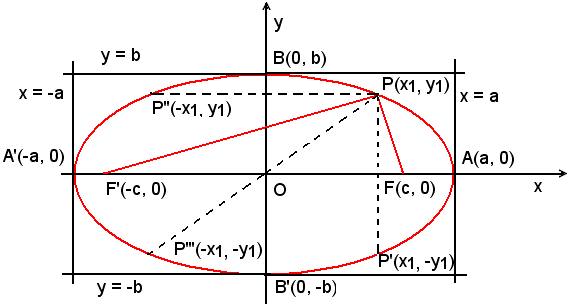
Esempi
1)-Scrivere l'equazione del luogo dei punti le cui distanze da F(4, 0) e da F'(-4, 0) hanno somma costante uguale a 10.
Sia P un punto generico del piano di coordinate x ed y; la distanza di P da F è data da:
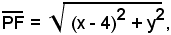
mentre quella di P da F' è data da
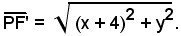
Il punto P(x, y) appartiene al luogo richiesto se soddisfa la condizione:
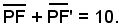
Sostituendo i valori trovati, si ottiene:
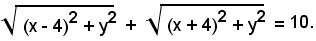
Passando il secondo radicale al secondo membro ed elevando al quadrato, si ha:
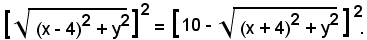
Sviluppando e riducendo, si ricava:
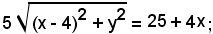
elevando ancora al quadrato, si ha:
25(x2 + 8x + 16 + y2) = 625 + 200x + 16x2,
semplificando
9x2 + 25y2 = 225
e dividendo per 225, segue
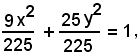
ed infine si ottiene
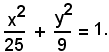
Il luogo richiesto è l'ellisse avente per centro l'origine O, per asse focale l'asse x e i semiassi di valore a = 5 e b = 3.
Più brevemente l'equazione dell'ellisse si può ricavare determinando direttamente i valori dei semiassi a e b.
L'ellisse ha per distanza focale c = 4 e semiasse maggiore a = 5.
Infatti, dalla relazione
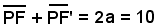
si ottiene
a = 5.
Dalla relazione (4) a2 - c2 = b2 si ricava:
b2 = 25 - 16 = 9,
ossia
b = 3.
L'equazione dell'ellisse è allora:
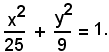
2)-Scrivere l'equazione del luogo dei punti le cui distanze da F(0, 3) e da F'(-40, -3) hanno somma costante uguale a 10.
Il luogo richiesto è un'ellisse avente per centro l'origine degli assi e per asse focale l'asse y.
Primo procedimento, vedi esempio precedente:
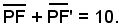
Inoltre si ha:
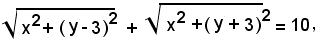
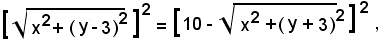
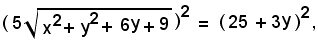
25 x2 + y2 = 400,
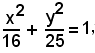
ellisse avente per centro l'origine O, asse focale l'asse y e di semiassi a = 4. b = 5.
Secondo procedimento, vedi esempio precedente:
c = 3, b = 5, a2 = b2- c2= 25 - 9 = 16,
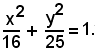
Il cerchio caso limite dell'ellisse
Quando i due fuochi F e F' dell'ellisse coincidono con il centro O, l'ellisse diventa un cerchio di centro O e raggio a.
Infatti, se la distanza è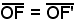 = c = 0, la (4) a2 - c2 = b2 diventa a2 = b2 e l'equazione dell'ellisse si riduce a:
= c = 0, la (4) a2 - c2 = b2 diventa a2 = b2 e l'equazione dell'ellisse si riduce a:
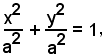
cioè
x2 + y2 = a2
che è l'equazione del cerchio di centro O e raggio a.
Si può quindi affermare che:
-un ellisse avente i semiassi uguali è un cerchio e i due fuochi coincidono nel centro O.
Costruzione dei fuochi di un ellisse
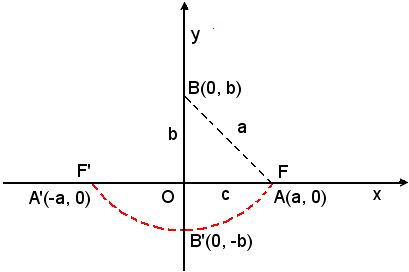
Data l'ellisse di equazione
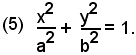
si vogliono costruire i suoi fuochi F(c, 0) e F'(-c, 0).
Allo scopo si segnano in un piano cartesiano i vertici della curva, intersezioni dell'ellisse con gli asse x ed y, A(a, 0), A'(-a, 0), B(0, b) e B'(0, -b). Dalla relazione (4) a2 - c2 = b2 si ha a2 = b2 + c2, quest'ultima esprime che un triangolo rettangolo avente ipotenusa uguale al semiasse maggiore a ed un cateto uguale al semiasse minore b, ha l'altro cateto uguale alla distanza c dei fuochi dall'origine. Con centro in B e raggio a, si descrive un arco di circonferenza; i punti in cui questo incontra l'asse x sono i fuochi F e F'.
Costruzione dell'ellisse
1)-Costruzione dell'ellisse con moto continuo, dati i fuochi e l'asse maggiore.
Siano F e F' i due fuochi e 2a l'asse maggiore. Si fissano in F e F' due spilli e a questi si legano i capi di un filo lungo 2a.
Si appoggia poi al filo, nel punto P, la punta di una matita, in modo da tenerlo fisso; poichè la somma delle distanze PF e PF' è uguale alla lunghezza del filo 2a, il punto P appartiene all'ellisse di asse maggiore 2a. Facendo scorrere la punta della matita contro il filo, l'ellisse viene descritto in modo continuo.
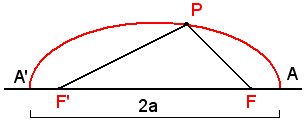
2)-Costruzione dell'ellisse per punti, dati i fuochi ed un punto P.
Siano F e F' i due fuochi e P un punto dell'ellisse.
Si riportino su una retta r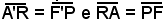 ; essendo P un punto dell'ellisse, si ha che il segmento
; essendo P un punto dell'ellisse, si ha che il segmento 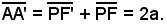
Preso sul segmento AA' un punto arbitrario N in modo che risulti |A'N - NA| ≤ F'F, siccome i cerchi di cui si parla risulteranno certamente secanti o tangenti, si descrive un arco di cerchio di centro di centro F' e raggio A'N ed un arco di cerchio di centro F e raggio NA, i punti T e T' in cui i due cerchi si incontrano, sono punti dell'ellisse.
Infatti, le loro distanze dai fuochi F e F' hanno per somma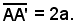
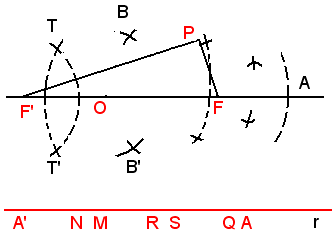
Ripetendo la costruzione a partire da altri punti del segmento AA', si trovano altri punti dell'ellisse. Si noti il punto M, medio di AA', permette la costruzione dei vertici secondari B e B'; e il punto Q distante di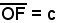 dal punto M, permette la costruzione del vertice A dell'asse maggiore.
dal punto M, permette la costruzione del vertice A dell'asse maggiore.
3)-Costruzione dell'ellisse per punti, dati i semiassi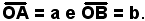
Siano AA' e BB' gli assi dell'ellisse in posizione e grandezza. Col compasso, si punta nel centro O e si descrivono due circonferenze aventi per raggi il semiasse minore OB e il semiasse maggiore OA. Ogni punto P(O, a) del cerchio, di centro O e raggio a, si trasforma in un punto P' dell'ellisse di semiassi a e b.
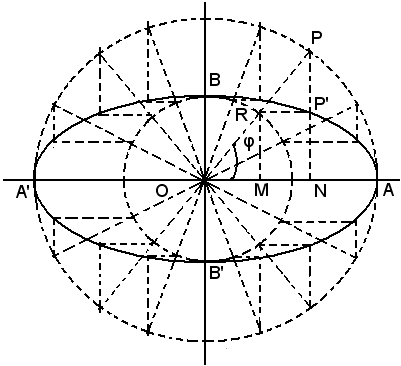
Il punto P' si ottiene conducendo da R, punto di intersezione del raggio OP con il cerchio di centro O e raggio a, la parallela all'asse x e da P la parallela all'asse y. Si dimostra che P' è effettivamente un punto dell'ellisse. Allo scopo, si indica con x,
con x, 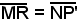 con y e con φ l'angolo che il raggio OP forma con l'asse x.
Dal triangolo rettangolo ONP, per un noto teorema di trigonometria,
con y e con φ l'angolo che il raggio OP forma con l'asse x.
Dal triangolo rettangolo ONP, per un noto teorema di trigonometria, 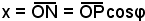 , ossia, essendo
, ossia, essendo 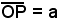 , risulta:
, risulta:
(8) x = acosφ.
Dal triangolo rettangolo OMR, si ricava , ossia, essendo
, ossia, essendo 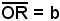 , risulta:
, risulta:
(9) y = bsenφ.
Dividendo la (8) e la (9) per b, si ottiene:
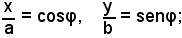
elevando al quadrato ambo membri e sommando, si ha:
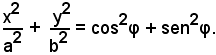
Ricordando che cos2φ + sen2φ = 1, infine si ha:
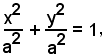
equazione dell'ellisse.
Equazioni parametriche dell'ellisse e del cerchio.
Le equazioni:
(10) x = acosφ, y = bsenφ,
ottenute in precedenza, si chiamano equazioni parametriche dell'ellisse.
Se a = b, l'ellisse diventa il cerchio di centro O e raggio a, le cui equazioni parametriche sono:
Se il cerchio ha per centro C (α, β), le (11) diventano:
Intersezioni dell'ellisse con una retta
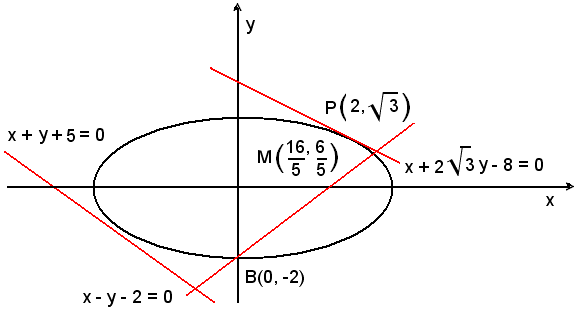
Determinare le intersezioni dell'ellisse:
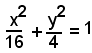
con le rette di equazioni
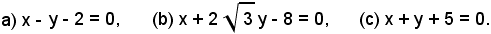
Le coordinate dei punti di intersezione dell'ellisse con una retta devono soddisfare l'equazione dell'ellisse, perchè i punti si trovano sull'ellisse, e l'equazione della retta, perchè i punti si trovano sulla retta; esse sono perciò le soluzioni del sistema formato dalle equazioni dell'ellisse e della retta. Quindi:
1)-le coordinate dei punti di intersezione dell'ellisse con la retta di equazione a) sono le soluzioni del sistema:
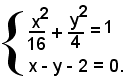
Ricavando il valore di y dalla seconda equazione e sostituendolo nella prima, si ha:
x2 + 16x =0,
da cui
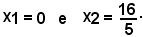
Sostituendo tali valori nella seconda equazione del sistema, si ha:
y1 = - 2 e y2 = 6 .
5
Quindi la retta di equazione a) è secante l'ellisse nei punti B(0, -2) e M(16/5, 6/5).
2)-le coordinate dei punti di intersezione dell'ellisse con la retta di equazione b) sono le soluzioni del sistema:
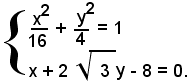
Ricavando il valore di x dalla seconda equazione e sostituendolo nella prima, si ha:
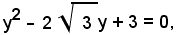
da cui
x1 = x2 = 2.
Quindi la retta di equazione b) è tangente all'ellisse nel punto:
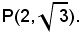
3)-le coordinate dei punti di intersezione dell'ellisse con la retta di equazione c) sono le soluzioni del sistema:
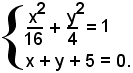
Ricavando il valore di x dalla seconda equazione e sostituendo nella prima, si ha:
5y2 + 10y + 9 = 0,
da cui, tenendo conto che l'unità immaginaria è data da
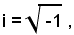
risulta
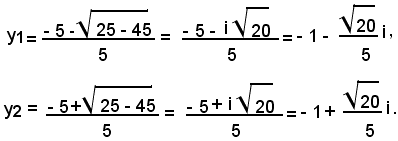
Le ordinate dei due punti di intersezione sono immaginarie, complesse e coniugate; sostituendo tali valori nella seconda equazione del sistema si trovano le ascisse, anch'esse immaginarie, complesse e coniugate. Quindi la retta di equazione c) è esterna all'ellisse.
Retta tangente all'ellisse in un suo punto
Data l'ellisse di equazione x2 + 4y2 = 8 e un suo punto P di coordinate 2 e 1, si vuole determinare l'equazione della retta tangente all'ellisse nel punto P.
Primo procedimento
L'equazione di una retta generica uscente da P(2, 1) è y - 1 = m(x - 2). Affinchè la retta sia tangente all'ellisse nel punto P, occorre che le due intersezioni retta-ellisse coincidano in P.
Le coordinate dei punti di intersezione retta-ellisse si trovano risolvendo il sistema:
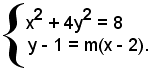
Ricavando il valore della y dalla seconda equazione e sostituendo nella prima, si ha:
a) (1 + 4m2)x2 + 8m(1- 2m)x + 16m2 - 16m - 4 = 0.
Affinchè le due intersezioni retta-ellisse coincidano, occorre che le radici dell'equazione precedente, che forniscono le ascisse dei punti comuni all'ellisse e alla retta, siano reali e coincidenti, cioè che il determinante della a) sia uguale a zero, ossia:
Δ = 16m2(1 - m)2 - (1 + 4m2)(16m2 - 16m - 4) = 0.
Sviluppando e semplificando, si ha:
4m2 + 4m + 1 = 0,
da cui
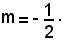
Sostituendo tale valore nell'equazione y - 1 = m(x - 2) si ottiene:
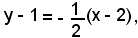
cioè
(b) x + 2y - 4 = 0.
equazione della tangente richiesta.
Secondo procedimento - Formula di sdoppiamento
La (b) si può ottenere direttamente applicando la formula di sdoppiamento, cioè sostituendo nell'equazione dell'ellisse x2 + 4y2 = 8 ad x2 il valore 2x, prodotto dell'ascissa 2 del punto P per la variabile x e ad ad y2 il valore 1· y, prodotto dell'ordinata 1 di P per la variabile y.
Infatti, si ha:
2x + 4(1· y) = 8,
cioè
2x + 4y - 8 = 0,
ossia
x + 2y - 4 = 0.
In generale:
-l'equazione della tangente all'ellisse
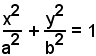
nel punto P(x0, y0) si ottiene sostituendo nell'equazione dell'ellisse ad x2 il valore xx0 e ad y2 il valore yy0, operazione analoga a quella della circonferenza.
La retta tangente all'ellisse nel punto P(x0, y0) la dunque equazione:
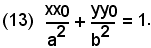
Se il punto P(x0, y0) non appartiene all'ellisse, la retta di equazione (13) si chiama polare del punto P rispetto all'ellisse. Essa rappresenta "la retta congiungente il punto di contatto delle due tangenti condotte dal punto P all'ellisse", analogamente a quanto visto per la polarità rispetto ad una circonferenza.
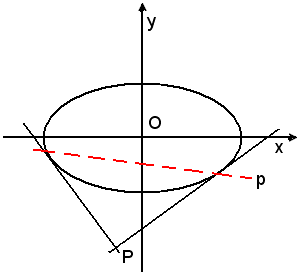
Se il punto P è esterno all'ellisse, la polare è secante. Essa si costruisce congiungendo i punti di contatto delle due tangenti condotte dal punto P alla curva. Se il punto P si trova sull'ellisse, la polare coincide con la tangente t in P alla curva.
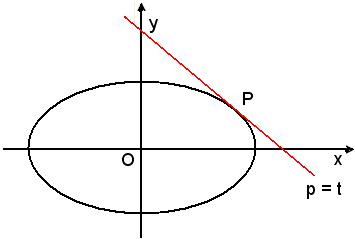
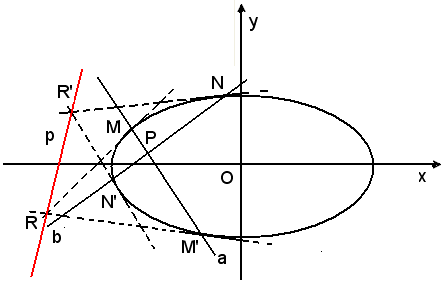
Se il punto P è interno all'ellisse, si conducono per P due rette a e b secanti la curva, per i punti di intersezione M, M' e N, N' di queste con l'ellisse le tangenti alla curva. La congiungente i due punti, poli, R e R' è la polare p richiesta.
Retta normale all'ellisse in un suo punto
Si chiama retta normale ad una curva in un punto "la perpendicolare in quel punto alla tangente alla curva".
Sia P(x0, y0) un punto dell'ellisse:
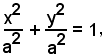
Si è visto che l'equazione della tangente all'ellisse è:
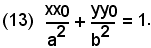
Si osserva ora che il suo coefficiente angolare è:
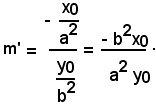
Per determinare l'equazione della normale in P all'ellisse, si scrive l'equazione di una retta generica per P, che è del tipo y - y0 = m(x - x0). Tale retta è perpendicolare alla (13) se il suo coefficiente angolare m è uguale all'opposto e reciproco di m', cioè
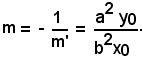
Dunque, l'equazione della normale in P(x0, y0) all'ellisse di equazione
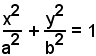
è:
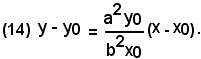
Esempio
Scrivere l'equazione della normale all'ellisse di equazione x2 + 4y2 = 8 nel punto P(2, 1).
Si scrive l'equazione di una retta generica per P(2, 1), y - 1 = m(x - 2); si determina l'equazione della tangente all'ellisse in P(2, 1) e, consigliando che è sempre preferibile applicare la formula di sdoppiamento, essa ha equazione x + 2y - 4 = 0.
Il coefficiente angolare della tangente è:
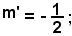
Il coefficiente angolare m della normale è uguale all'opposto e reciproco di m', quindi:
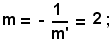
sostituendo tale valore nella y - 1 = m(x - 2), si ottiene l'equazione della normale richiesta:
y - 1 = 2(x - 2).
cioè
2x - y - 3 = 0.
COMPLEMENTI
Proprietà delle tangenti e delle normali all'ellisse
Data l'ellisse di fuochi F e F', siano P un suo punto generico, t la retta tangente e n la retta normale all'ellisse nel punto P. Si vuole dimostrare che:
-se P è un punto dell'ellisse, la bisettrice t dell'angolo esterno in P del triangolo F'PF è tangente all'ellisse.
Basta dimostrare che ogni altro punto Q di t distinto da P non appartiene all'ellisse.
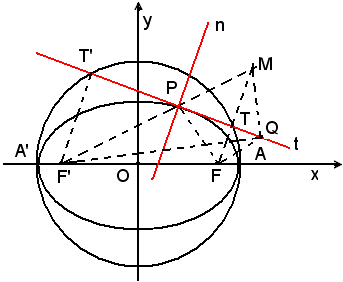
Infatti, se M è il simmetrico di F rispetto alla tangente t, questa risulta asse di FM. Se Q appartiene all'ellisse, si ha:
F'Q + QF = F'P + PF,
ossia
F'Q + QM = F'P + PM = F'M,
e ciò è assurdo, perchè nel triangolo F'QM, la somma dei lati F'Q + QM > F'M'. Pertanto si conclude che:
-la tangente t e la normale n all'ellisse in un suo punto P sono le bisettrici degli angoli, FPM e FPF', formati dalle rette che congiungono quel punto con i fuochi.
Esempio
Data l'ellisse
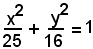
ed il punto
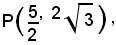
scrivere le equazioni delle rette che congiungono il punto P con i fuochi F(3, 0) e F'(-3, 0); trovare le bisettrici dell'angolo formato da queste e verificare che tali bisettrici rappresentano la tangente e la normale in P all'ellisse.
Le rette PF e PF' hanno rispettivamente equazioni:
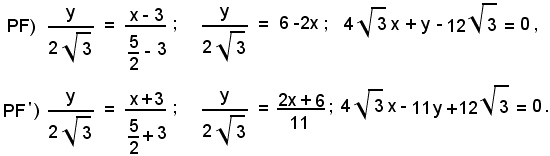
Le bisettrici degli angoli formati dalle rette PF e PF', come si è visto, hanno equazioni:
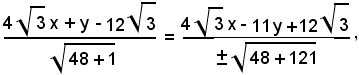
cioè
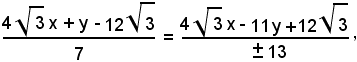
da cui
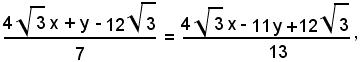
ossia
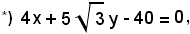
e
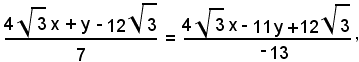
cioè
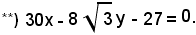
Le equazioni della tangente e della normale in P all'ellisse sono rispettivamente *) e **), cioè:
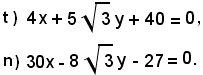
E' così dimostrato che le rette t e n coincidono con le bisettrici a) e b).
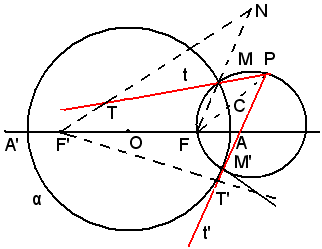
Podaria dei fuochi rispetto all'ellisse
La podaria di un fuoco rispetto all'ellisse è il luogo dei piedi delle perpendicolari condotte da questo fuoco alle tangenti all'ellisse.
In generale, si chiama podaria di un punto P rispetto ad una curva γ il luogo dei piedi delle perpendicolari condotte dal punto alle tangenti alla curva γ.
In figura sono rappresentati il punto P, la curva γ e le tangenti ad essa t, t', t'', t'''. I punti A, B, C, D, piedi delle perpendicolari condotte alle tangenti, sono punti della podaria γ', evidenziata in rosso.
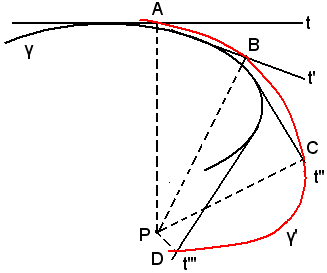
Si dimostra che:
-la podaria dei fuochi rispetto ad un'ellisse è il cerchio che ha per diametro l'asse maggiore dell'ellisse.
Considerata la figura precedente alla suddetta, già esaminata in precedenza, si congiunge il punto T con O, essendo T il piede della perpendicolare condotta dal fuoco F alla tangente all'ellisse in P. Il segmento OT, essendo O il punto medio di FF' e T il punto medio del segmento FM, è parallelo al lato F'M del triangolo FF'M e uguale alla metà di esso, cioè, essendo F'M = F'P + PM = F'P + PF = 2a, risulta:
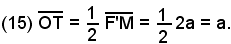
La (15) esprime che T, piede della perpendicolare condotta dal fuoco alla tangente generica t, dista dal centro O dell'ellisse di un segmento costante uguale al semiasse maggiore; quindi il luogo dei punti T è il cerchio che ha per centro O e raggio a. Allo stesso risultato si perviene se invece del fuoco F si considera il fuoco F'.
COSTRUZIONI
Costruzione dell'ellisse per tangenti
Dati i due fuoichi F e F' di un'ellisse e l'asse maggiore AA', si vuole costruire la curva per tangenti.
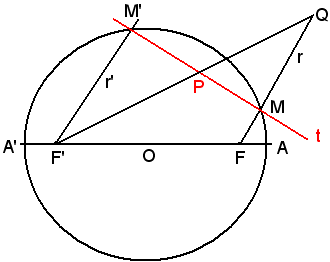
Allo scopo, si traccia il cerchio di centro O e diametro AA', podaria del fuoco rispetto all'ellisse e per i fuochi F e F' si conducono due semirette parallele concordi r ed r'; siano M ed M' le intersezioni con il cerchio, la retta MM' è una delle tangenti cercate, come si può notare dalla prima figura dei Complementi.
Il punto di contatto P si costruisce come segue:
si porta sulla retta r il segmento MQ = FM e si congiunge Q con F'; l'intersezione della F'Q con la MM' è il punto di contatto richiesto.
Ripetendo la costruzione con altre coppie di parallele uscenti dai fuochi si trovano altre tangenti e relativi punti di contatto.
Condurre da un punto dato P le tangenti all'ellisse di cui si conoscono asse maggiore ed i fuochi F ed F'.
Si traccia con diametro AA' e centro O il cerchio α podaria dei fuochi rispetto all'ellisse. Sia M un punto qualsiasi del cerchio α la perpendicolare in M alla MF è tangente all'ellisse, Affinchè questa passi per P, occorre che M appartenga alla circonferenza di diametro FP. Le rette PM e PM', ove M ed M' sono le intersezioni del cerchio di diametro FP con il cerchio α, sono le tangenti t e t' richieste. Per determinare i punti di contatto, si costruiscono i simmetrici di F rispetto alle tangenti t e t' e siano N e M', si congiungano tali punti con F': le intersezioni di tali congiungenti con t e t' forniscono i punti di contatto T e T'.
Eccentricità - Direttrice
Data l'ellisse di equazione
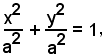
si chiama direttrice, coniugata, del fuoco f, la retta d perpendicolare all'asse focale, passante per il punto M(a2/c, 0), con a > c segue (a2/c) > a, cioè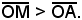
Si vuole dimostrare che:
-ogni punto dell'ellisse gode della proprietà che il rapporto delle sue distanze dal fuoco F e dalla relativa direttrice d è costante.
Tale rapporta vale c/a = e, ed è chiamato eccentricità dell'ellisse.
Si considerino le coordinate x ed y di un punto generico P del piano, la cui distanza da F è:
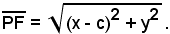
La distanza di P dalla retta direttrice d è uguale, come è noto, a:
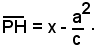
Scrivendo analiticamente la condizione:
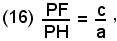
si ottiene
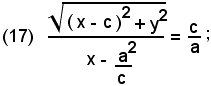
elevando al quadrato e semplificando, si ha
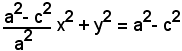
ossia, essendo a2 - c2 = b2,
b2x2 + a2y2 = a2b2,
da cui, dividendo per a2b2,
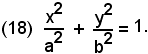
La (18) fornisce la condizione necessaria e sufficiente affinchè i punti P(x, y) del piano appartengano all'ellisse, dunque: tutti e soli i punti dell'ellisse godono effettivamente della proprietà enunciata. Si può quindi affermare che:
-il luogo geometrico dei punti del piano per cui è costante ed uguale a c/a = e < 1, il rapporto delle distanze da un punto fisso, fuoco, e da una retta fissa, direttrice, è un'ellisse.
Come al fuoco F corrisponde la direttrice d, così al fuoco F' corrisponde la direttrice d', perpendicolare all'asse focale, di equazione x = a2/c ed è ancora, costante ed uguale a c/a, il rapporto delle distanze di un punto P dell'ellesse dal fuoco F' e dalla relativa direttrice d'. Dall'essere c < a, l'eccentricità e = c/a dell'ellisse è sempre minore di 1. La forma dell'ellisse è legata all'eccentricità; più il valore di e si approssima ad 1, più l'ellisse è allungata.
Se a = b, l'ellisse si riduce ad un cerchio e poichè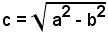 si annulla, l'eccentricità e = 0; il cerchio è, dunque, un'ellisse con eccentricità nulla.
si annulla, l'eccentricità e = 0; il cerchio è, dunque, un'ellisse con eccentricità nulla.
Nota bene
Le direttrici sono le polari dei fuochi F e F' rispetto all'ellisse.
Infatti le equazioni delle polari dei punti F(c, 0), essendo F e F' interni all'ellisse le polari sono esterne, rispetto all'ellisse
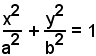
sono rispettivamente:
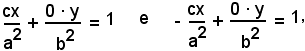
ossia
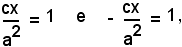
cioè
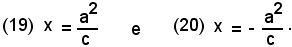
Si indicano con:
-F e F' i due fuochi,
-2c la lunghezza del segmento FF',
-2a la somma costante delle distanze di un punto generico P dell'ellisse dai punti F e F'.
Dalla definizione di ellisse, si ha:

Poichè in un triangolo un lato è minore della somma degli altri due, nel triangolo FPF' dev'essere:
ossia
2c < 2a,
cioè
c < a.
Quest'ultima è la diseguaglianza fondamentale dell'ellisse.
Poichè F'F = 2c, le coordinate dei fuochi sono F(c, 0) e F'(-c, 0).

Indicando con x ed y le coordinate del generico punto P dell'ellisse, risulta:
avendo applicato le formule dalla distanza di due punti.
Sostituendo tali valori nella (1), si ha:
che per c < a rappresenta l'ellisse.
Si libera ora l'equazione irrazionale (2) dai radicali, portando il secondo radicale al secondo membro ed elevando al quadrato, si ha
cioè
Isolando il radicale e riducendo, si ottiene:
dividendo ambo i membri per 4, risulta
elevando al quadrato ambo i membri, si ha
a2 + [ x2 + 2cx + c2 + y2 ] = a4 + 2a2cx + c2x2
e semplificando, si trova
(3) (a2 - c2)x2 + a2y2 = a2(a2 - c2).
Essendo a > c, segue che a2 - c2 > 0 e quindi si può porre:
(4) a2 - c2 = b2
e sostituendo, la (3) diventa
b2x2+ a2y2 = a2b2,
dividendo ambo i membri per a2b2, infine si ottiene
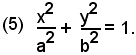
La (5) si chiama equazione canonica dell'ellisse.
a)-Proprietà di simmetria
L'ellisse di equazione (5) è simmetrica rispetto agli assi x, y è all'origine delle coordinate.
Si vuole dimostrare che se il punto P di coordinate x1 ed y1 appartiene all'ellisse, cioè le coordinate x1 ed y1 soddisfano l'equazione (5), ossia si verifica :
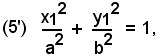
anche i punti P'(x1, -y1), P''(-x1, y1) e P'''(-x1, -y1), rispettivamente simmetrici del punto P rispetto all'asse x, all'asse y e all'origine, appartengono all'ellisse.

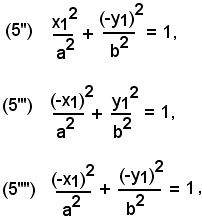
le quali esprimono rispettivamente l'appartenenza all'ellisse dei punti P'(x1, -y1), P''(-x1, y1) e P'''(-x1, -y1).
Nota bene
Generalità sulle curve
1)-Se nell'equazione di una curva algebrica la variabile y compare elevata soltanto a potenza pari, la curva è simmetrica rispetto all'asse x.
Infatti, se l'equazione della curva è soddisfatta dalle coordinate x1 e y1 di un punto P, essa è soddisfatta anche dalle coordinate x1, -y1 del punto P' rispetto all'asse x, in quanto elevando a potenza pari, il segno meno scompare. Così l'equazione x2y2 + x2 - y2 = 0, in cui la y compare soltanto in potenza di grado pari, rappresenta una curva algebrica simmetrica rispetto all'asse x.
Infatti, se la curva passa per P(x1, y1), cioè se x12y12 + x12 - y12 = 0, è anche x12(-y1)2 + x12 - (-y1)2 = 0, cioè la curva passa per P'(x1, -y1).
2)-Se nell'equazione di una curva algebrica la variabile x compare elevata soltanto a potenza pari, la curva è simmetrica rispetto all'asse y.
Così l'equazione x4 + y3 + x2 - y - 1 = 0, in cui la x compare soltanto in potenze di grado pari, rappresenta una curva algebrica simmetrica rispetto all'asse y.
Infatti, se la curva passa per P(x1, y1), cioè se x14 + y13 + x12 - y1 - 1 = 0, è anche (-x1)4 + y13 + (-x1)2 - y1 - 1 = 0, cioè la curva passa per P''(-x1, y1).
3)-Se nell'equazione di una curva algebrica tutti i termini sono di grado pari nella x e nella y, oppure i termini sono di grado dispari nella x e nella y, la curva è simmetrica rispetto all'origine.
Così l'equazione x2y2 + x2 - y2 = 0, che ha tutti i termini di grado pari nella x e nella y, rappresenta una curva algebrica simmetrica rispetto all'origine.
Infatti, se P(x1, y1) appartiene alla curva, cioè se x12y12 + x12 - y12 = 0, è anche
( -x1)2(-y1)2 + (-x1)2 - (-y1)2 = 0, cioè la curva passa per P'''(-x1, -y1).
Così dicasi per la curva di equazione x3 + y3 + x = 0.
b)-Vertici
Le intersezioni dell'ellisse con l'asse y si trovano risolvendo il sistema:
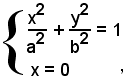
da cui
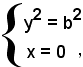
ossia
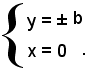
L'ellisse incontra l'asse y nei punti B(0, b) e B'(0, -b), che si chiamano vertici secondari; il segmento
E' bene osservare che, essendo a > 0 e b > 0, dalla relazione (4) a2 - c2 = b2 si ricava a2 > b2, cioè a > b, quindi 2a > 2b, ossia
c)-Risolvendo l'equazione dell'ellisse rispetto alla variabile y, si ha:
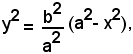
ossia
Affinchè la y abbia valori reali, occorre che:
a2- x2 ≥ 0,
ossia
cioè
-a ≤ x ≤ a.
Si ricordi che la condizione di realtà per un radicale di indice pari è che il radicando sia positivo o nullo. La radice di indice pari di una quantità negativa è immaginaria.
Si
hanno allora punti reali della curva soltanto nell'interno della
striscia di piano limitata dalle rette x = a e x = -a, rette tangenti
all'ellisse, rispettivamente nei vertici A e A'.
Risolvendo invece l'equazione dell'ellisse rispetto alla variabile x, si ha:
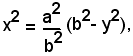
Risolvendo invece l'equazione dell'ellisse rispetto alla variabile x, si ha:
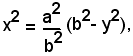
ossia
Affinchè la x abbia valori reali, occorre che:
b2- y2 ≥ 0,
ossia
|y| ≤ a,
cioè
-b ≤ y ≤ b.
Si hanno allora i punti reali della curva soltanto nell'interno della striscia di piano limitata dalle rette y = b e y = -b, rette tangenti all'ellisse, rispettivamente nei vertici B e B'.
y = ± b. La curva ha l'andamento indicato nella figura seguente.

Esempi
1)-Scrivere l'equazione del luogo dei punti le cui distanze da F(4, 0) e da F'(-4, 0) hanno somma costante uguale a 10.
Sia P un punto generico del piano di coordinate x ed y; la distanza di P da F è data da:
mentre quella di P da F' è data da
Il punto P(x, y) appartiene al luogo richiesto se soddisfa la condizione:
Sostituendo i valori trovati, si ottiene:
Passando il secondo radicale al secondo membro ed elevando al quadrato, si ha:
Sviluppando e riducendo, si ricava:
elevando ancora al quadrato, si ha:
25(x2 + 8x + 16 + y2) = 625 + 200x + 16x2,
semplificando
9x2 + 25y2 = 225
e dividendo per 225, segue
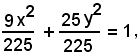
ed infine si ottiene
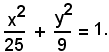
Il luogo richiesto è l'ellisse avente per centro l'origine O, per asse focale l'asse x e i semiassi di valore a = 5 e b = 3.
Più brevemente l'equazione dell'ellisse si può ricavare determinando direttamente i valori dei semiassi a e b.
L'ellisse ha per distanza focale c = 4 e semiasse maggiore a = 5.
Infatti, dalla relazione
si ottiene
a = 5.
Dalla relazione (4) a2 - c2 = b2 si ricava:
b2 = 25 - 16 = 9,
ossia
b = 3.
L'equazione dell'ellisse è allora:
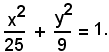
2)-Scrivere l'equazione del luogo dei punti le cui distanze da F(0, 3) e da F'(-40, -3) hanno somma costante uguale a 10.
Il luogo richiesto è un'ellisse avente per centro l'origine degli assi e per asse focale l'asse y.
Primo procedimento, vedi esempio precedente:
Inoltre si ha:
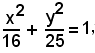
ellisse avente per centro l'origine O, asse focale l'asse y e di semiassi a = 4. b = 5.
Secondo procedimento, vedi esempio precedente:
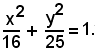
Il cerchio caso limite dell'ellisse
Quando i due fuochi F e F' dell'ellisse coincidono con il centro O, l'ellisse diventa un cerchio di centro O e raggio a.
Infatti, se la distanza è
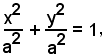
cioè
x2 + y2 = a2
che è l'equazione del cerchio di centro O e raggio a.
Si può quindi affermare che:
-un ellisse avente i semiassi uguali è un cerchio e i due fuochi coincidono nel centro O.
Costruzione dei fuochi di un ellisse

Data l'ellisse di equazione
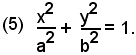
si vogliono costruire i suoi fuochi F(c, 0) e F'(-c, 0).
Allo scopo si segnano in un piano cartesiano i vertici della curva, intersezioni dell'ellisse con gli asse x ed y, A(a, 0), A'(-a, 0), B(0, b) e B'(0, -b). Dalla relazione (4) a2 - c2 = b2 si ha a2 = b2 + c2, quest'ultima esprime che un triangolo rettangolo avente ipotenusa uguale al semiasse maggiore a ed un cateto uguale al semiasse minore b, ha l'altro cateto uguale alla distanza c dei fuochi dall'origine. Con centro in B e raggio a, si descrive un arco di circonferenza; i punti in cui questo incontra l'asse x sono i fuochi F e F'.
Costruzione dell'ellisse
1)-Costruzione dell'ellisse con moto continuo, dati i fuochi e l'asse maggiore.
Siano F e F' i due fuochi e 2a l'asse maggiore. Si fissano in F e F' due spilli e a questi si legano i capi di un filo lungo 2a.

Si appoggia poi al filo, nel punto P, la punta di una matita, in modo da tenerlo fisso; poichè la somma delle distanze PF e PF' è uguale alla lunghezza del filo 2a, il punto P appartiene all'ellisse di asse maggiore 2a. Facendo scorrere la punta della matita contro il filo, l'ellisse viene descritto in modo continuo.
2)-Costruzione dell'ellisse per punti, dati i fuochi ed un punto P.
Siano F e F' i due fuochi e P un punto dell'ellisse.
Si riportino su una retta r
Preso sul segmento AA' un punto arbitrario N in modo che risulti |A'N - NA| ≤ F'F, siccome i cerchi di cui si parla risulteranno certamente secanti o tangenti, si descrive un arco di cerchio di centro di centro F' e raggio A'N ed un arco di cerchio di centro F e raggio NA, i punti T e T' in cui i due cerchi si incontrano, sono punti dell'ellisse.
Infatti, le loro distanze dai fuochi F e F' hanno per somma

Ripetendo la costruzione a partire da altri punti del segmento AA', si trovano altri punti dell'ellisse. Si noti il punto M, medio di AA', permette la costruzione dei vertici secondari B e B'; e il punto Q distante di
3)-Costruzione dell'ellisse per punti, dati i semiassi
Siano AA' e BB' gli assi dell'ellisse in posizione e grandezza. Col compasso, si punta nel centro O e si descrivono due circonferenze aventi per raggi il semiasse minore OB e il semiasse maggiore OA. Ogni punto P(O, a) del cerchio, di centro O e raggio a, si trasforma in un punto P' dell'ellisse di semiassi a e b.

Il punto P' si ottiene conducendo da R, punto di intersezione del raggio OP con il cerchio di centro O e raggio a, la parallela all'asse x e da P la parallela all'asse y. Si dimostra che P' è effettivamente un punto dell'ellisse. Allo scopo, si indica
Dal triangolo rettangolo OMR, si ricava
(9) y = bsenφ.
Dividendo la (8) e la (9) per b, si ottiene:
elevando al quadrato ambo membri e sommando, si ha:
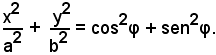
Ricordando che cos2φ + sen2φ = 1, infine si ha:
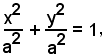
equazione dell'ellisse.
Equazioni parametriche dell'ellisse e del cerchio.
Le equazioni:
(10) x = acosφ, y = bsenφ,
ottenute in precedenza, si chiamano equazioni parametriche dell'ellisse.
Se a = b, l'ellisse diventa il cerchio di centro O e raggio a, le cui equazioni parametriche sono:
(11) x = acosφ, y = asenφ.
Se il cerchio ha per centro C (α, β), le (11) diventano:
(12) x - α = acosφ, y - β = asenφ,
Intersezioni dell'ellisse con una retta
Determinare le intersezioni dell'ellisse:
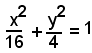
con le rette di equazioni
Le coordinate dei punti di intersezione dell'ellisse con una retta devono soddisfare l'equazione dell'ellisse, perchè i punti si trovano sull'ellisse, e l'equazione della retta, perchè i punti si trovano sulla retta; esse sono perciò le soluzioni del sistema formato dalle equazioni dell'ellisse e della retta. Quindi:
1)-le coordinate dei punti di intersezione dell'ellisse con la retta di equazione a) sono le soluzioni del sistema:
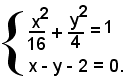
Ricavando il valore di y dalla seconda equazione e sostituendolo nella prima, si ha:
x2 + 16x =0,
da cui
Sostituendo tali valori nella seconda equazione del sistema, si ha:
y1 = - 2 e y2 = 6 .
5
Quindi la retta di equazione a) è secante l'ellisse nei punti B(0, -2) e M(16/5, 6/5).
2)-le coordinate dei punti di intersezione dell'ellisse con la retta di equazione b) sono le soluzioni del sistema:
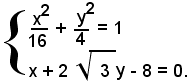
Ricavando il valore di x dalla seconda equazione e sostituendolo nella prima, si ha:
da cui
x1 = x2 = 2.
Quindi la retta di equazione b) è tangente all'ellisse nel punto:
3)-le coordinate dei punti di intersezione dell'ellisse con la retta di equazione c) sono le soluzioni del sistema:
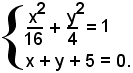
Ricavando il valore di x dalla seconda equazione e sostituendo nella prima, si ha:
5y2 + 10y + 9 = 0,
da cui, tenendo conto che l'unità immaginaria è data da
risulta
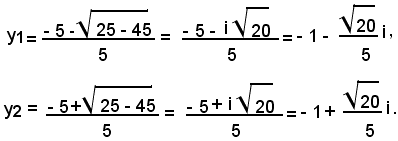
Le ordinate dei due punti di intersezione sono immaginarie, complesse e coniugate; sostituendo tali valori nella seconda equazione del sistema si trovano le ascisse, anch'esse immaginarie, complesse e coniugate. Quindi la retta di equazione c) è esterna all'ellisse.

Retta tangente all'ellisse in un suo punto
Data l'ellisse di equazione x2 + 4y2 = 8 e un suo punto P di coordinate 2 e 1, si vuole determinare l'equazione della retta tangente all'ellisse nel punto P.
Primo procedimento
L'equazione di una retta generica uscente da P(2, 1) è y - 1 = m(x - 2). Affinchè la retta sia tangente all'ellisse nel punto P, occorre che le due intersezioni retta-ellisse coincidano in P.
Le coordinate dei punti di intersezione retta-ellisse si trovano risolvendo il sistema:
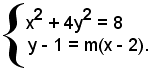
Ricavando il valore della y dalla seconda equazione e sostituendo nella prima, si ha:
a) (1 + 4m2)x2 + 8m(1- 2m)x + 16m2 - 16m - 4 = 0.
Affinchè le due intersezioni retta-ellisse coincidano, occorre che le radici dell'equazione precedente, che forniscono le ascisse dei punti comuni all'ellisse e alla retta, siano reali e coincidenti, cioè che il determinante della a) sia uguale a zero, ossia:
Δ = 16m2(1 - m)2 - (1 + 4m2)(16m2 - 16m - 4) = 0.
Sviluppando e semplificando, si ha:
4m2 + 4m + 1 = 0,
da cui
Sostituendo tale valore nell'equazione y - 1 = m(x - 2) si ottiene:
cioè
(b) x + 2y - 4 = 0.
equazione della tangente richiesta.
Secondo procedimento - Formula di sdoppiamento
La (b) si può ottenere direttamente applicando la formula di sdoppiamento, cioè sostituendo nell'equazione dell'ellisse x2 + 4y2 = 8 ad x2 il valore 2x, prodotto dell'ascissa 2 del punto P per la variabile x e ad ad y2 il valore 1· y, prodotto dell'ordinata 1 di P per la variabile y.
Infatti, si ha:
cioè
2x + 4y - 8 = 0,
ossia
x + 2y - 4 = 0.
In generale:
-l'equazione della tangente all'ellisse
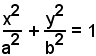
nel punto P(x0, y0) si ottiene sostituendo nell'equazione dell'ellisse ad x2 il valore xx0 e ad y2 il valore yy0, operazione analoga a quella della circonferenza.
La retta tangente all'ellisse nel punto P(x0, y0) la dunque equazione:
Se il punto P(x0, y0) non appartiene all'ellisse, la retta di equazione (13) si chiama polare del punto P rispetto all'ellisse. Essa rappresenta "la retta congiungente il punto di contatto delle due tangenti condotte dal punto P all'ellisse", analogamente a quanto visto per la polarità rispetto ad una circonferenza.

Se il punto P è esterno all'ellisse, la polare è secante. Essa si costruisce congiungendo i punti di contatto delle due tangenti condotte dal punto P alla curva. Se il punto P si trova sull'ellisse, la polare coincide con la tangente t in P alla curva.


Se il punto P è interno all'ellisse, si conducono per P due rette a e b secanti la curva, per i punti di intersezione M, M' e N, N' di queste con l'ellisse le tangenti alla curva. La congiungente i due punti, poli, R e R' è la polare p richiesta.
Retta normale all'ellisse in un suo punto
Si chiama retta normale ad una curva in un punto "la perpendicolare in quel punto alla tangente alla curva".
Sia P(x0, y0) un punto dell'ellisse:
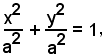
Si è visto che l'equazione della tangente all'ellisse è:
Si osserva ora che il suo coefficiente angolare è:
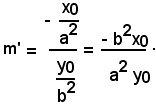
Per determinare l'equazione della normale in P all'ellisse, si scrive l'equazione di una retta generica per P, che è del tipo y - y0 = m(x - x0). Tale retta è perpendicolare alla (13) se il suo coefficiente angolare m è uguale all'opposto e reciproco di m', cioè
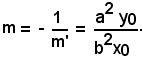
Dunque, l'equazione della normale in P(x0, y0) all'ellisse di equazione
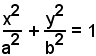
è:
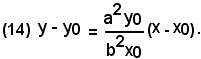
Esempio
Scrivere l'equazione della normale all'ellisse di equazione x2 + 4y2 = 8 nel punto P(2, 1).
Si scrive l'equazione di una retta generica per P(2, 1), y - 1 = m(x - 2); si determina l'equazione della tangente all'ellisse in P(2, 1) e, consigliando che è sempre preferibile applicare la formula di sdoppiamento, essa ha equazione x + 2y - 4 = 0.
Il coefficiente angolare della tangente è:
Il coefficiente angolare m della normale è uguale all'opposto e reciproco di m', quindi:
sostituendo tale valore nella y - 1 = m(x - 2), si ottiene l'equazione della normale richiesta:
y - 1 = 2(x - 2).
cioè
2x - y - 3 = 0.
COMPLEMENTI
Proprietà delle tangenti e delle normali all'ellisse
Data l'ellisse di fuochi F e F', siano P un suo punto generico, t la retta tangente e n la retta normale all'ellisse nel punto P. Si vuole dimostrare che:
-se P è un punto dell'ellisse, la bisettrice t dell'angolo esterno in P del triangolo F'PF è tangente all'ellisse.
Basta dimostrare che ogni altro punto Q di t distinto da P non appartiene all'ellisse.

Infatti, se M è il simmetrico di F rispetto alla tangente t, questa risulta asse di FM. Se Q appartiene all'ellisse, si ha:
F'Q + QF = F'P + PF,
ossia
F'Q + QM = F'P + PM = F'M,
e ciò è assurdo, perchè nel triangolo F'QM, la somma dei lati F'Q + QM > F'M'. Pertanto si conclude che:
-la tangente t e la normale n all'ellisse in un suo punto P sono le bisettrici degli angoli, FPM e FPF', formati dalle rette che congiungono quel punto con i fuochi.
Esempio
Data l'ellisse
ed il punto
scrivere le equazioni delle rette che congiungono il punto P con i fuochi F(3, 0) e F'(-3, 0); trovare le bisettrici dell'angolo formato da queste e verificare che tali bisettrici rappresentano la tangente e la normale in P all'ellisse.
Le rette PF e PF' hanno rispettivamente equazioni:
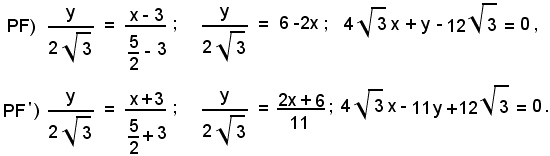
Le bisettrici degli angoli formati dalle rette PF e PF', come si è visto, hanno equazioni:
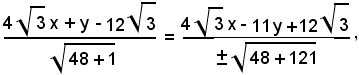
cioè
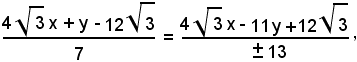
da cui
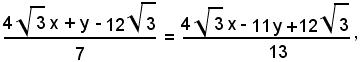
ossia
e
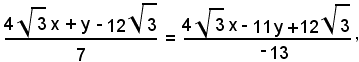
Le equazioni della tangente e della normale in P all'ellisse sono rispettivamente *) e **), cioè:
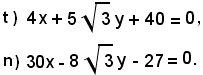
E' così dimostrato che le rette t e n coincidono con le bisettrici a) e b).
Podaria dei fuochi rispetto all'ellisse
La podaria di un fuoco rispetto all'ellisse è il luogo dei piedi delle perpendicolari condotte da questo fuoco alle tangenti all'ellisse.
In generale, si chiama podaria di un punto P rispetto ad una curva γ il luogo dei piedi delle perpendicolari condotte dal punto alle tangenti alla curva γ.
In figura sono rappresentati il punto P, la curva γ e le tangenti ad essa t, t', t'', t'''. I punti A, B, C, D, piedi delle perpendicolari condotte alle tangenti, sono punti della podaria γ', evidenziata in rosso.

Si dimostra che:
-la podaria dei fuochi rispetto ad un'ellisse è il cerchio che ha per diametro l'asse maggiore dell'ellisse.
Considerata la figura precedente alla suddetta, già esaminata in precedenza, si congiunge il punto T con O, essendo T il piede della perpendicolare condotta dal fuoco F alla tangente all'ellisse in P. Il segmento OT, essendo O il punto medio di FF' e T il punto medio del segmento FM, è parallelo al lato F'M del triangolo FF'M e uguale alla metà di esso, cioè, essendo F'M = F'P + PM = F'P + PF = 2a, risulta:
La (15) esprime che T, piede della perpendicolare condotta dal fuoco alla tangente generica t, dista dal centro O dell'ellisse di un segmento costante uguale al semiasse maggiore; quindi il luogo dei punti T è il cerchio che ha per centro O e raggio a. Allo stesso risultato si perviene se invece del fuoco F si considera il fuoco F'.
Costruzione dell'ellisse per tangenti
Dati i due fuoichi F e F' di un'ellisse e l'asse maggiore AA', si vuole costruire la curva per tangenti.

Allo scopo, si traccia il cerchio di centro O e diametro AA', podaria del fuoco rispetto all'ellisse e per i fuochi F e F' si conducono due semirette parallele concordi r ed r'; siano M ed M' le intersezioni con il cerchio, la retta MM' è una delle tangenti cercate, come si può notare dalla prima figura dei Complementi.
Il punto di contatto P si costruisce come segue:
si porta sulla retta r il segmento MQ = FM e si congiunge Q con F'; l'intersezione della F'Q con la MM' è il punto di contatto richiesto.
Ripetendo la costruzione con altre coppie di parallele uscenti dai fuochi si trovano altre tangenti e relativi punti di contatto.
Condurre da un punto dato P le tangenti all'ellisse di cui si conoscono asse maggiore ed i fuochi F ed F'.
Si traccia con diametro AA' e centro O il cerchio α podaria dei fuochi rispetto all'ellisse. Sia M un punto qualsiasi del cerchio α la perpendicolare in M alla MF è tangente all'ellisse, Affinchè questa passi per P, occorre che M appartenga alla circonferenza di diametro FP. Le rette PM e PM', ove M ed M' sono le intersezioni del cerchio di diametro FP con il cerchio α, sono le tangenti t e t' richieste. Per determinare i punti di contatto, si costruiscono i simmetrici di F rispetto alle tangenti t e t' e siano N e M', si congiungano tali punti con F': le intersezioni di tali congiungenti con t e t' forniscono i punti di contatto T e T'.

Eccentricità - Direttrice
Data l'ellisse di equazione
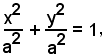
si chiama direttrice, coniugata, del fuoco f, la retta d perpendicolare all'asse focale, passante per il punto M(a2/c, 0), con a > c segue (a2/c) > a, cioè

Si vuole dimostrare che:
-ogni punto dell'ellisse gode della proprietà che il rapporto delle sue distanze dal fuoco F e dalla relativa direttrice d è costante.
Tale rapporta vale c/a = e, ed è chiamato eccentricità dell'ellisse.
Si considerino le coordinate x ed y di un punto generico P del piano, la cui distanza da F è:
La distanza di P dalla retta direttrice d è uguale, come è noto, a:
Scrivendo analiticamente la condizione:
si ottiene
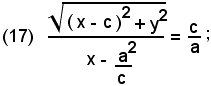
elevando al quadrato e semplificando, si ha
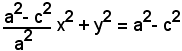
ossia, essendo a2 - c2 = b2,
b2x2 + a2y2 = a2b2,
da cui, dividendo per a2b2,
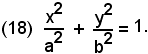
La (18) fornisce la condizione necessaria e sufficiente affinchè i punti P(x, y) del piano appartengano all'ellisse, dunque: tutti e soli i punti dell'ellisse godono effettivamente della proprietà enunciata. Si può quindi affermare che:
-il luogo geometrico dei punti del piano per cui è costante ed uguale a c/a = e < 1, il rapporto delle distanze da un punto fisso, fuoco, e da una retta fissa, direttrice, è un'ellisse.
Come al fuoco F corrisponde la direttrice d, così al fuoco F' corrisponde la direttrice d', perpendicolare all'asse focale, di equazione x = a2/c ed è ancora, costante ed uguale a c/a, il rapporto delle distanze di un punto P dell'ellesse dal fuoco F' e dalla relativa direttrice d'. Dall'essere c < a, l'eccentricità e = c/a dell'ellisse è sempre minore di 1. La forma dell'ellisse è legata all'eccentricità; più il valore di e si approssima ad 1, più l'ellisse è allungata.
Se a = b, l'ellisse si riduce ad un cerchio e poichè
Nota bene
Le direttrici sono le polari dei fuochi F e F' rispetto all'ellisse.
Infatti le equazioni delle polari dei punti F(c, 0), essendo F e F' interni all'ellisse le polari sono esterne, rispetto all'ellisse
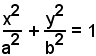
sono rispettivamente:
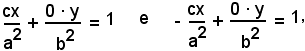
ossia
cioè