MIKY & GENNY
EQUAZIONI DEL PIANO ---> INDICE
I punti dello spazio, le cui coordinate (x, y, z) sono tutte e sole le soluzioni di un'equazione di primo grado del tipo:
(1) ax + by + cz + d = 0,
appartengono al piano rappresentato dalla (1), che si chiama equazione del piano.
Viceversa, qualsiasi equazione di primo grado nelle variabili x, y, z rappresenta un piano.
Un punto P(x0, y0, z0) appartiene ad un piano, quando e solo quando le sue coordinate sono soluzioni dell'equazione del piano, cioè quando si verifica:
ax0 + by0 + cz0 + d = 0.
Nota bene
Si osservi che: qualsiasi equazione nelle variabili x, y, z rappresenta una superficie, luogo di punti dello spazio le cui coordinate soddisfano tale equazione.
Il grado dell'equazione della superficie si chiama ordine della superficie.
Il piano è una superficie del primo ordine, le superfici del secondo ordine si chiamano quadriche.
Si osservi come l'equazione (1) abbia infinite soluzioni che si ottengono assegnando a due delle tre variabili scelte a piacere, valori arbitrari e, di conseguenza resta determinato il valore della terza.
Se nella (1) a = b = d = 0, l'equazione diventa z = 0, cioè quella del piano coordinato π1 coincidente con il piano xy.
Se nella (1) a = c = d = 0, l'equazione diventa y = 0, cioè quella del piano coordinato π3 coincidente con il piano zx.
Se nella (1) d = 0, l'equazione diventa:
ax + by + cz = 0
e rappresenta un piano passante per l'origine.
Nell'equazione (1) si rilevano i quattro coefficienti a, b, c, d, di cui tre essenziali, potendo sempre considerare i mutui rapporti di tre di essi rispetto al quarto, diverso da zero.
Dunque, per individuare un piano, occorre assegnare tre condizioni lineari:
-per tre punti non allineati, passa uno ed un solo piano.
Equazione segmentaria di un piano
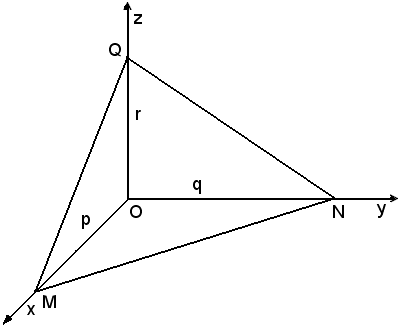
Le coordinate dei punti d'intersezione M, N, Q di un piano di equazione ax + by + cz + d = 0 con gli assi coordinati sono date dalle soluzioni dei sistemi:
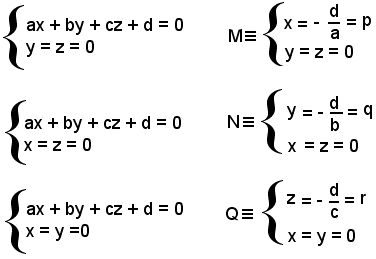
e
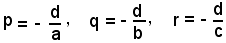
si chiamano intercette del piano (1) con gli assi coordinati.
Viceversa, dati p, q, r, l'equazione del piano è:
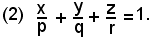
Infatti, dividendo la (1) per d e cambiando di segno, si ha:
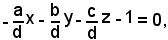
ossia
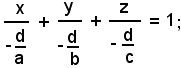
ponendo
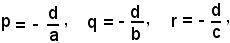
si ha la (2).
Esempi
1)-Determinare l'equazione del piano passante per i punti O(0, 0, 0), A(1, 1, 1), B(1, -1, 0).
I punti, O, A, B appartengono al piano di equazione (1) ax + by + cz + d = 0, se le loro coordinate sono soluzioni dell'equazione del piano.
Sostituendo di seguito nella (1) ad x, y e z le coordinate dei punti O, A, B, si ha il sistema:
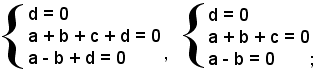
posto c = 1, si ottiene
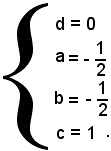
L'equazione del piano richiesto è:
x + y - 2z = 0.
2)-Scrivere l'equazione del piano avente per intercette p = 2, q = 3, r = 4.
L'equazione del piano richiesto è:
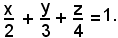
Distanza di due punti
La distanza di due punti P(x1, y1, z1) e P'(x2, y2, z2) si calcola immediatamente.
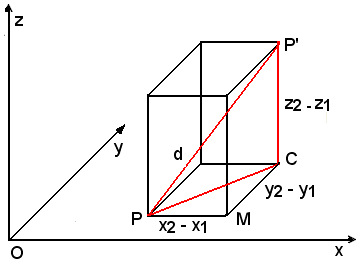
Si consideri il parallelepipedo rettangolo di spigoli paralleli agli assi e di vertici opposti P e P'.
I tre spigoli PM, MC, CP' hanno lunghezze uguali alle differenze delle coordinate, cioè:
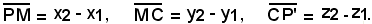
Per il teorema di Pitagora:
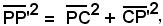
essendo

si ottiene
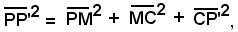
quindi
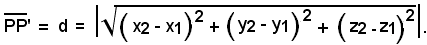
(1) ax + by + cz + d = 0,
appartengono al piano rappresentato dalla (1), che si chiama equazione del piano.
Viceversa, qualsiasi equazione di primo grado nelle variabili x, y, z rappresenta un piano.
Un punto P(x0, y0, z0) appartiene ad un piano, quando e solo quando le sue coordinate sono soluzioni dell'equazione del piano, cioè quando si verifica:
Nota bene
Si osservi che: qualsiasi equazione nelle variabili x, y, z rappresenta una superficie, luogo di punti dello spazio le cui coordinate soddisfano tale equazione.
Il grado dell'equazione della superficie si chiama ordine della superficie.
Il piano è una superficie del primo ordine, le superfici del secondo ordine si chiamano quadriche.
Si osservi come l'equazione (1) abbia infinite soluzioni che si ottengono assegnando a due delle tre variabili scelte a piacere, valori arbitrari e, di conseguenza resta determinato il valore della terza.
Se nella (1) a = b = d = 0, l'equazione diventa z = 0, cioè quella del piano coordinato π1 coincidente con il piano xy.
Se nella (1) b = c = d = 0, l'equazione diventa x = 0, cioè quella del piano coordinato π2 coincidente con il piano yz.
Se nella (1) a = c = d = 0, l'equazione diventa y = 0, cioè quella del piano coordinato π3 coincidente con il piano zx.
Se nella (1) d = 0, l'equazione diventa:
e rappresenta un piano passante per l'origine.
Nell'equazione (1) si rilevano i quattro coefficienti a, b, c, d, di cui tre essenziali, potendo sempre considerare i mutui rapporti di tre di essi rispetto al quarto, diverso da zero.
Dunque, per individuare un piano, occorre assegnare tre condizioni lineari:
-per tre punti non allineati, passa uno ed un solo piano.
Equazione segmentaria di un piano
Le coordinate dei punti d'intersezione M, N, Q di un piano di equazione ax + by + cz + d = 0 con gli assi coordinati sono date dalle soluzioni dei sistemi:
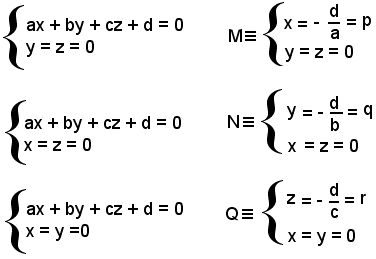
e
si chiamano intercette del piano (1) con gli assi coordinati.
Viceversa, dati p, q, r, l'equazione del piano è:
Infatti, dividendo la (1) per d e cambiando di segno, si ha:
ossia
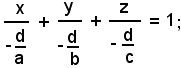
ponendo
si ha la (2).

Esempi
1)-Determinare l'equazione del piano passante per i punti O(0, 0, 0), A(1, 1, 1), B(1, -1, 0).
I punti, O, A, B appartengono al piano di equazione (1) ax + by + cz + d = 0, se le loro coordinate sono soluzioni dell'equazione del piano.
Sostituendo di seguito nella (1) ad x, y e z le coordinate dei punti O, A, B, si ha il sistema:
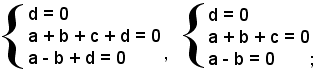
posto c = 1, si ottiene
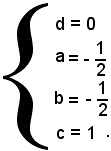
L'equazione del piano richiesto è:
2)-Scrivere l'equazione del piano avente per intercette p = 2, q = 3, r = 4.
L'equazione del piano richiesto è:
Distanza di due punti
La distanza di due punti P(x1, y1, z1) e P'(x2, y2, z2) si calcola immediatamente.

Si consideri il parallelepipedo rettangolo di spigoli paralleli agli assi e di vertici opposti P e P'.
I tre spigoli PM, MC, CP' hanno lunghezze uguali alle differenze delle coordinate, cioè:
Per il teorema di Pitagora:
essendo
si ottiene
quindi