MIKY & GENNY
EQUAZIONI DELLA RETTA ---> INDICE
Si consideri l'equazione:
(1) 2x + 3y - 6 = 0,
di primo grado nelle variabili x ed y.
E' noto dall'algebra che un'equazione in due incognite ammette infinite soluzioni.
Tali soluzioni si ottengono assegnando ad una delle incognite, alla x o alla y, un valore a piacere e si risolve l'equazione data rispetto all'altra indeterminata, y o x, dopo aver sostituito in essa all'incognita prescelta, x o y, il valore fissato.
Quindi, assegnando alla x certi valori, si hanno i seguenti valori per la y:
per x=1 la (1) diventa: 2·1 + 3y - 6 = 0, ossia 2 + 3y - 6 = 0, da cui 3y - 4 = 0, cioè y = 4/3.
In tal modo si è ottenuta la prima soluzione x = 1, y = 4/3;
(1) 2x + 3y - 6 = 0,
di primo grado nelle variabili x ed y.
E' noto dall'algebra che un'equazione in due incognite ammette infinite soluzioni.
Tali soluzioni si ottengono assegnando ad una delle incognite, alla x o alla y, un valore a piacere e si risolve l'equazione data rispetto all'altra indeterminata, y o x, dopo aver sostituito in essa all'incognita prescelta, x o y, il valore fissato.
Quindi, assegnando alla x certi valori, si hanno i seguenti valori per la y:
per x=1 la (1) diventa: 2·1 + 3y - 6 = 0, ossia 2 + 3y - 6 = 0, da cui 3y - 4 = 0, cioè y = 4/3.
In tal modo si è ottenuta la prima soluzione x = 1, y = 4/3;
per x=2 la (1) diventa: 2·2 + 3y - 6 = 0, ossia 4 + 3y - 6 = 0, da cui 3y - 2 = 0, cioè y = 2/3.
In tal modo si è ottenuta la seconda soluzione x = 2, y = 2/3;
per x=3 la (1) diventa: 2·3 + 3y - 6 = 0, ossia 6 + 3y - 6 = 0, da cui 3y = 0, cioè y =0.
In tal modo si è ottenuta la terza soluzione x = 3, y =0;
per x=4 la (1) diventa: 2·4 + 3y - 6 = 0, ossia 8 + 3y - 6 = 0, da cui 3y + 2 = 0, cioè y = -2/3.
In tal modo si è ottenuta la quarta soluzione x = 4, y = -2/3:
per x=5 la (1) diventa: 2·5 + 3y - 6 = 0, ossia 10 + 3y - 6 = 0, da cui 3y + 4 = 0, cioè y = -4/3.
In tal modo si è ottenuta la quinta soluzione x = 5, y = -4/3.
per x=6 la (1) diventa: 2·6 + 3y - 6 = 0, ossia 12 + 3y - 6 = 0, da cui 3y + 6 = 0, cioè y = -2.
In tal modo si è ottenuta la sesta soluzione x = 6, y = -2.
Si riportano ora, in un piano cartesiano, i punti che hanno per coordinate le coppie dei valori trovati, indicati come segue:
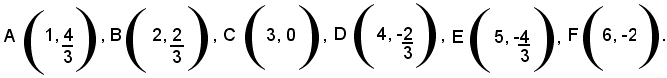
Si dice che tutti questi punti, le cui coordinate sono soluzioni dell'equazione data, sono rappresentati dall'equazione 2x + 3y - 6 = 0.
Dalla figura si vede che tutti questi punti sono allineati.
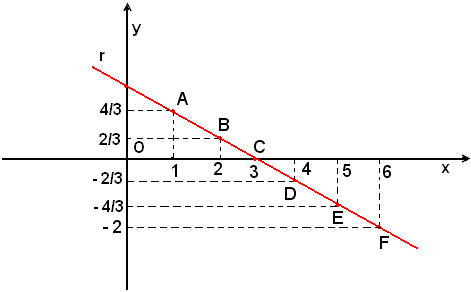
L'equazione 2x + 3y - 6 = 0 rappresenta la retta tracciata r. Le soluzioni dell'equazione (1) sono dunque coordinate di punti della retta r e viceversa, tutti i punti della retta r hanno per coordinate soluzioni dell'equazione (1).
La retta si chiama grafico o rappresentazione geometrica dell'equazione 2x + 3y - 6 = 0.
Le proprietà che i punti del piano, le cui coordinate soddisfano l'equazione (1), siano allineati, non è caratteristica della particolare equazione considerata, ma è caratteristica di tutte le equazioni del tipo:
(2) ax + by + c = 0,
cioè tutti i punti del piano le cui coordinate (x, y) soddisfano l'equazione (2), sono allineati.
Si può quindi affermare quanto segue:
-in un piano cartesiano ogni retta, senza eccezioni, è rappresentata da un'equazione di primo grado nelle incognite x ed y, del tipo ax + by + c = 0 e viceversa, ogni equazione del tipo ax + by + c = 0 rappresenta nel piano una retta.
Nota bene
Da quanto ora affermato, risulta una corrispondenza biunivoca fra enti geometrici ed enti analitici, poichè all'ente geometrico "retta" corrisponde l'ente analitico "equazione lineare" e viceversa. Le proprietà simmetriche delle rette, come si vedrà in seguito, si tradurranno in proprietà algebriche delle loro equazioni.
Poichè nell'equazione ax + by + c = 0, i coefficienti a, b delle incognite e c, termine noto, possono assumere valori qualsiasi, con la sola limitazione di non essere contemporaneamente nulli i coefficienti di a e di b, si dice che l'equazione (2) dipende dai valori dei rapporti di due suoi coefficienti rispetto al terzo, supposto diverso da zero, per cui suol dirsi che l'equazione (2) dipende da due coefficienti essenziali. Da ciò si ricava che, per individuare una retta, poichè nell'equazione corrispondente esistono due coefficienti essenziali, sono necessari almeno due punti distinti.
Se a, b, c, fossero simultaneamente nulli, l'equazione diventerebbe un'identità.
Esempio
Tracciare la retta di equazione x + 2y - 6 = 0.
Poichè una retta è individuata da due suoi punti distinti, e poichè i punti di una retta devono avere per coordinate soluzioni dell'equazione x + 2y - 6 = 0, è sufficiente procurarsi due soluzioni dell'equazione data, segnare nel piano cartesiano i punti corrispondenti e quindi la retta che li congiunge. Le coppie di valori (x, y) che soddisfano l'equazione della retta, si ottengono dando alla x o dalla y un valore arbitrario e risolvendo l'equazione rispetto all'altra incognita.
per x=2 l'equazione diventa: 2 + 2y - 6 = 0, ossia 2y - 4 = 0, da cui y = 2.
In tal modo si sono ottenute le coordinate del primo punto M (2, 2);
per x=4 l'equazione diventa: 4 + 2y - 6 = 0, ossia 2y - 2 = 0, da cui y = 1.
In tal modo si sono ottenute le coordinate del secondo punto N (4, 1).
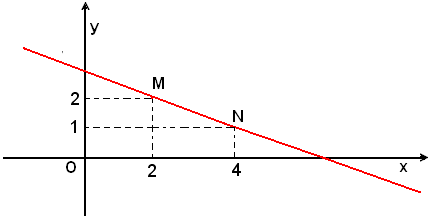
Segnati i due punti M ed N nel piano cartesiano, si può disegnare la retta, tenendo presente che conviene determinare punti lontani, le cui coordinate siano numeri interi.
Equazioni di rette in posizioni particolari
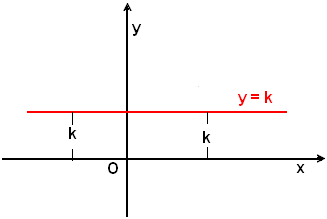
a)-Rette parallele all'asse x. Asse x.
Quando nell'equazione ax + by + c =0, a=0, l'equazione si riduce a by + c = 0, cioè y = -c/b e ponendo -c/b = k, si ha:
(3) y = k.
Tale relazione impone all'ordinata y di assumere lo stesso valore k, mentre l'ascissa x può assumere qualsiasi valore.
Tutti i punti che hanno ordinata k, e ascissa qualsiasi, stanno su una retta parallela all'asse x, distante da questo, in valore e segno, -c/b =k. Perciò l'equazione (3) rappresenta una retta parallela all'asse x. Viceversa, una retta parallela all'asse x è il luogo geometrico dei punti del piano aventi la stessa ordinata. Tali punti soddisfano un'equazione del tipo y = k.
Quindi:
se nell'equazione di una retta manca il termine in x, la retta è parallela all'asse x, e viceversa.
In generale l'equazione di una retta parallela all'asse x è del tipo:
y = k.
Nota bene
Si deve ricordare che l'ascissa del punto P nel piano cartesiano rappresenta la misura della distanza di P dall'asse y e l'ordinata di P la misura della distanza di P dall'asse x.
Si deve inoltre osservare che comunemente si dice:
"i punti del piano soddisfano l'equazione y = f(x)", invece di "le coordinate dei punti del piano soddisfano l'equazione y = f(x)";
"la retta ax + by + c = 0", invece di "la retta di equazione ax + by + c = 0".
b)-Rette parallele all'asse y. Asse y.
Quando nell'equazione ax + by + c = 0, b = 0, l'equazione si riduce ad ax + c = 0, cioè x = -c/a e ponendo -c/a = h, si ha:
(4) x = h.
Tale relazione impone all'ascissa x di assumere lo stesso valore h, mentre l'ordinata y può assumere qualsiasi valore. Tutti i punti che hanno ascissa h, e ordinata qualsiasi, stanno su una retta parallela all'asse y, distante da questo in valore e segno, -c/a =h.
Perciò l'equazione (4) rappresenta una retta parallela all'asse y. Viceversa, una retta parallela all'asse y è il luogo geometrico dei punti del piano aventi la stessa ascissa.
x = h.
Quindi:
se nell'equazione di una retta manca il termine in y, la retta è parallela all'asse y, e viceversa.
In generale l'equazione di una retta parallela all'asse y è del tipo:
(5) x = h.
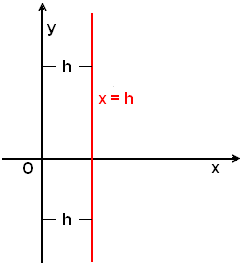
In particolare se h = 0, si ha l'equazione dell'asse y.
Dunque:
l'asse y è il luogo geometrico dei punti del piano aventi ascisse nulle ed ha equazione:
(6) x = 0.
c)-Rette passanti per l'origine
Quando nell'equazione ax + by + c = 0, c=0, l'equazione si riduce ad ax + by = 0, ed è soddisfatta dai valori x = 0 e y = 0, quindi rappresenta una retta che passa per il punto di coordinate (0, 0), cioè per l'origine. Quindi:
-se l'equazione di una retta manca del termine noto, la retta passa per l'origine, e viceversa.
Nota bene
Si deve ricordare che la bisettrice di un angolo è "il luogo dei punti del piano equidistanti dai lati dell'angolo".
In tema di notazioni, in seguito con le lettere x ed y saranno indicate le coordinate di un punto generico di una retta, con x0 ed y0 o con x1 ed y1 le coordinate di un un punto ben determinato.
d)-Bisettrici degli angoli formati dagli assi
La retta r, bisettrice del primo e terzo quadrante, è il luogo geometrico dei punti aventi ascissa uguale all'ordinata in valore e segno, entrambe positive nel primo quadrante, entrambe negative nel terzo. La sua equazione è:
(7) x = y.
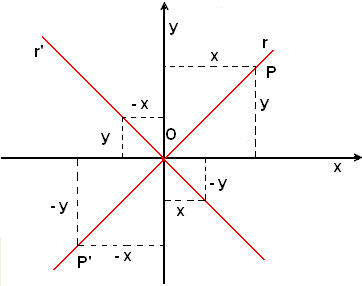
La retta r, bisettrice del secondo e quarto quadrante, è il luogo geometrico dei punti aventi ascissa ed ordinata uguali in valore assoluto ma di segno opposto, ascissa negativa e ordinata positiva nel secondo quadrante, ascissa positiva e ordinata negativa nel quarto quadrante, entrambe negative nel terzo. La sua equazione è:
(8) x = - y.
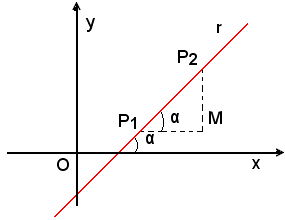
Retta per due puntiSia P (x, y) un punto generico di r. Dalla similitudine dei triangoli P1NP e P1MP2, come da figura, si ricava:
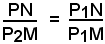
ed essendo
si ha l'equazione lineare in x ed y
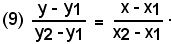
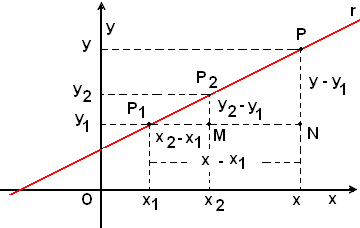
La (9) rappresenta la condizione di allineamento dei punti P1, P2, P per cui si può affermare:
-condizione necessaria e sufficiente affinchè tre punti P1(x1, y1), P2(x2, y2), P (x, y) siano allineati è che tra le loro coordinate sussista la relazione (9).
La relazione (9) è priva di significato quando si considera la retta parallela ad uno degli assi, cioè quando i due punti dati P1 e P2 hanno la stessa ascissa, retta parallela all'asse y, o la stessa ordinata, retta parallela all'asse x. Nel primo caso si avrebbe x2 -x1 = 0 e nel secondo y2 -y1 = 0; ma sarebbe valida comunque la relazione (9') (y2 -y1)(x -x1) = (x2 -x1)( y -y1), ottenuta dalla (9).
Esempi
1)-Determinare l'equazione della retta r congiungente i punti P1(2, - 3) e P2(- 3, 1).
Essendo x1 = 2, x2 = - 3, y1 = - 3, y2 = 1, indicando con x ed y le coordinate di un punto generico della retta r e applicando la (9), si ha;
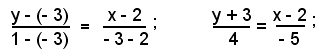
dopo facili calcoli, risulta
4x + 5y - 8 + 15 = 0,
ossia
4x + 5y + 7 =0.
Verifica: l'equazione 4x + 5y + 7 = 0 rappresenta la retta congiungente i punti P1 e P2, se le coordinate di P1 e P2 soddisfano l'equazione. Le coordinate di P1 sono x1 = 2, y1 = - 3, sostituendo 2 alla x e 3 alla y nell'equazione suddetta, si ha:
4 · 2 - 3 · 5 + 7 = 8 + -15 + 7 = 15 - 15 = 0.
Cioè (2, - 3) rappresenta una soluzione dell'equazione 4x + 5y + 7 = 0 e quindi P1 appartiene alla retta r. Procedendo allo stesso modo per P2(-3, 1), si ha:
4 · (-3) + 5 · 5(1) + 7 = - 12 + + 5 + 7 = 12 - 12 = 0.
Quindi anche P2 appartiene alla retta r.
2)-Determinare l'equazione della retta r congiungente i punti P1(-2, 3) e P2(- 2, 5).
Essendo x1 = - 2, x2 = - 2, y1 = 3, y2 = 5, indicando con x ed y le coordinate di un punto generico della retta r, applicando la (9), si ha;
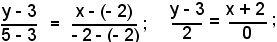
espressione priva di significato perchè contiene zero al denominatore.
Per eliminare tale inconveniente, si applica la relazione (9') (y2 - y1)( x - x1) = (x2 - x1)( y - y1) e si ha:
(5 - 3)(x + 2) = 0(y - y1);
2(x + 2) = 0;
x + 2 = 0;
x = - 2
che rappresenta l'equazione della retta parallela all'asse y.
Nota bene
L'equazione della retta r congiungente i punti P1(-2, 3) e P2(- 2, 5), poteva determinarsi direttamente osservando che i punti P1 e P2 hanno la stessa ascissa, cioè la stessa distanza dall'asse y, e quindi devono appartenere alla retta di equazione x = - 2.
3)-Determinare l'equazione della retta r congiungente i punti P1(1, 4) e P2(3, 4).
0= 2(y - 4);
y - 4 = 0.
y = 4.
Fascio di rette
In tal modo si è ottenuta la seconda soluzione x = 2, y = 2/3;
per x=3 la (1) diventa: 2·3 + 3y - 6 = 0, ossia 6 + 3y - 6 = 0, da cui 3y = 0, cioè y =0.
In tal modo si è ottenuta la terza soluzione x = 3, y =0;
per x=4 la (1) diventa: 2·4 + 3y - 6 = 0, ossia 8 + 3y - 6 = 0, da cui 3y + 2 = 0, cioè y = -2/3.
In tal modo si è ottenuta la quarta soluzione x = 4, y = -2/3:
per x=5 la (1) diventa: 2·5 + 3y - 6 = 0, ossia 10 + 3y - 6 = 0, da cui 3y + 4 = 0, cioè y = -4/3.
In tal modo si è ottenuta la quinta soluzione x = 5, y = -4/3.
per x=6 la (1) diventa: 2·6 + 3y - 6 = 0, ossia 12 + 3y - 6 = 0, da cui 3y + 6 = 0, cioè y = -2.
In tal modo si è ottenuta la sesta soluzione x = 6, y = -2.
Si riportano ora, in un piano cartesiano, i punti che hanno per coordinate le coppie dei valori trovati, indicati come segue:
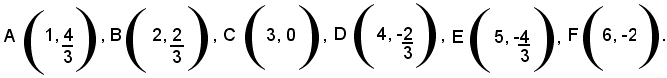
Si dice che tutti questi punti, le cui coordinate sono soluzioni dell'equazione data, sono rappresentati dall'equazione 2x + 3y - 6 = 0.
Dalla figura si vede che tutti questi punti sono allineati.
L'equazione 2x + 3y - 6 = 0 rappresenta la retta tracciata r. Le soluzioni dell'equazione (1) sono dunque coordinate di punti della retta r e viceversa, tutti i punti della retta r hanno per coordinate soluzioni dell'equazione (1).
La retta si chiama grafico o rappresentazione geometrica dell'equazione 2x + 3y - 6 = 0.
Le proprietà che i punti del piano, le cui coordinate soddisfano l'equazione (1), siano allineati, non è caratteristica della particolare equazione considerata, ma è caratteristica di tutte le equazioni del tipo:
cioè tutti i punti del piano le cui coordinate (x, y) soddisfano l'equazione (2), sono allineati.
Si può quindi affermare quanto segue:
-in un piano cartesiano ogni retta, senza eccezioni, è rappresentata da un'equazione di primo grado nelle incognite x ed y, del tipo ax + by + c = 0 e viceversa, ogni equazione del tipo ax + by + c = 0 rappresenta nel piano una retta.
Nota bene
Da quanto ora affermato, risulta una corrispondenza biunivoca fra enti geometrici ed enti analitici, poichè all'ente geometrico "retta" corrisponde l'ente analitico "equazione lineare" e viceversa. Le proprietà simmetriche delle rette, come si vedrà in seguito, si tradurranno in proprietà algebriche delle loro equazioni.
Poichè nell'equazione ax + by + c = 0, i coefficienti a, b delle incognite e c, termine noto, possono assumere valori qualsiasi, con la sola limitazione di non essere contemporaneamente nulli i coefficienti di a e di b, si dice che l'equazione (2) dipende dai valori dei rapporti di due suoi coefficienti rispetto al terzo, supposto diverso da zero, per cui suol dirsi che l'equazione (2) dipende da due coefficienti essenziali. Da ciò si ricava che, per individuare una retta, poichè nell'equazione corrispondente esistono due coefficienti essenziali, sono necessari almeno due punti distinti.
Se a, b, c, fossero simultaneamente nulli, l'equazione diventerebbe un'identità.
Esempio
Tracciare la retta di equazione x + 2y - 6 = 0.
Poichè una retta è individuata da due suoi punti distinti, e poichè i punti di una retta devono avere per coordinate soluzioni dell'equazione x + 2y - 6 = 0, è sufficiente procurarsi due soluzioni dell'equazione data, segnare nel piano cartesiano i punti corrispondenti e quindi la retta che li congiunge. Le coppie di valori (x, y) che soddisfano l'equazione della retta, si ottengono dando alla x o dalla y un valore arbitrario e risolvendo l'equazione rispetto all'altra incognita.
per x=2 l'equazione diventa: 2 + 2y - 6 = 0, ossia 2y - 4 = 0, da cui y = 2.
In tal modo si sono ottenute le coordinate del primo punto M (2, 2);
per x=4 l'equazione diventa: 4 + 2y - 6 = 0, ossia 2y - 2 = 0, da cui y = 1.
In tal modo si sono ottenute le coordinate del secondo punto N (4, 1).
Segnati i due punti M ed N nel piano cartesiano, si può disegnare la retta, tenendo presente che conviene determinare punti lontani, le cui coordinate siano numeri interi.
Equazioni di rette in posizioni particolari
a)-Rette parallele all'asse x. Asse x.
Quando nell'equazione ax + by + c =0, a=0, l'equazione si riduce a by + c = 0, cioè y = -c/b e ponendo -c/b = k, si ha:
(3) y = k.
Tale relazione impone all'ordinata y di assumere lo stesso valore k, mentre l'ascissa x può assumere qualsiasi valore.
Tutti i punti che hanno ordinata k, e ascissa qualsiasi, stanno su una retta parallela all'asse x, distante da questo, in valore e segno, -c/b =k. Perciò l'equazione (3) rappresenta una retta parallela all'asse x. Viceversa, una retta parallela all'asse x è il luogo geometrico dei punti del piano aventi la stessa ordinata. Tali punti soddisfano un'equazione del tipo y = k.
Quindi:
se nell'equazione di una retta manca il termine in x, la retta è parallela all'asse x, e viceversa.
In generale l'equazione di una retta parallela all'asse x è del tipo:
y = k.
Nota bene
Si deve ricordare che l'ascissa del punto P nel piano cartesiano rappresenta la misura della distanza di P dall'asse y e l'ordinata di P la misura della distanza di P dall'asse x.
Si deve inoltre osservare che comunemente si dice:
"i punti del piano soddisfano l'equazione y = f(x)", invece di "le coordinate dei punti del piano soddisfano l'equazione y = f(x)";
"la retta ax + by + c = 0", invece di "la retta di equazione ax + by + c = 0".
In particolare se k = 0, si ha l'equazione dell'asse x.
Dunque:
-l'asse x è il luogo geometrico dei punti del piano aventi ordinate nulle ed ha equazione:
Dunque:
-l'asse x è il luogo geometrico dei punti del piano aventi ordinate nulle ed ha equazione:
y = 0.
b)-Rette parallele all'asse y. Asse y.
Quando nell'equazione ax + by + c = 0, b = 0, l'equazione si riduce ad ax + c = 0, cioè x = -c/a e ponendo -c/a = h, si ha:
(4) x = h.
Tale relazione impone all'ascissa x di assumere lo stesso valore h, mentre l'ordinata y può assumere qualsiasi valore. Tutti i punti che hanno ascissa h, e ordinata qualsiasi, stanno su una retta parallela all'asse y, distante da questo in valore e segno, -c/a =h.
Perciò l'equazione (4) rappresenta una retta parallela all'asse y. Viceversa, una retta parallela all'asse y è il luogo geometrico dei punti del piano aventi la stessa ascissa.
Tali punti soddisfano un'equazione del tipo.
x = h.
Quindi:
se nell'equazione di una retta manca il termine in y, la retta è parallela all'asse y, e viceversa.
In generale l'equazione di una retta parallela all'asse y è del tipo:
In particolare se h = 0, si ha l'equazione dell'asse y.
Dunque:
l'asse y è il luogo geometrico dei punti del piano aventi ascisse nulle ed ha equazione:
(6) x = 0.
c)-Rette passanti per l'origine
Quando nell'equazione ax + by + c = 0, c=0, l'equazione si riduce ad ax + by = 0, ed è soddisfatta dai valori x = 0 e y = 0, quindi rappresenta una retta che passa per il punto di coordinate (0, 0), cioè per l'origine. Quindi:
-se l'equazione di una retta manca del termine noto, la retta passa per l'origine, e viceversa.
Nota bene
Si deve ricordare che la bisettrice di un angolo è "il luogo dei punti del piano equidistanti dai lati dell'angolo".
In tema di notazioni, in seguito con le lettere x ed y saranno indicate le coordinate di un punto generico di una retta, con x0 ed y0 o con x1 ed y1 le coordinate di un un punto ben determinato.
d)-Bisettrici degli angoli formati dagli assi
La retta r, bisettrice del primo e terzo quadrante, è il luogo geometrico dei punti aventi ascissa uguale all'ordinata in valore e segno, entrambe positive nel primo quadrante, entrambe negative nel terzo. La sua equazione è:
(7) x = y.
La retta r, bisettrice del secondo e quarto quadrante, è il luogo geometrico dei punti aventi ascissa ed ordinata uguali in valore assoluto ma di segno opposto, ascissa negativa e ordinata positiva nel secondo quadrante, ascissa positiva e ordinata negativa nel quarto quadrante, entrambe negative nel terzo. La sua equazione è:
(8) x = - y.
Retta per due punti
Si vuole determinare l'equazione della retta passante per i punti P1(x1, y1) e P2(x2, y2).
ed essendo
si ha l'equazione lineare in x ed y
La (9) rappresenta la condizione di allineamento dei punti P1, P2, P per cui si può affermare:
-condizione necessaria e sufficiente affinchè tre punti P1(x1, y1), P2(x2, y2), P (x, y) siano allineati è che tra le loro coordinate sussista la relazione (9).
La relazione (9) è priva di significato quando si considera la retta parallela ad uno degli assi, cioè quando i due punti dati P1 e P2 hanno la stessa ascissa, retta parallela all'asse y, o la stessa ordinata, retta parallela all'asse x. Nel primo caso si avrebbe x2 -x1 = 0 e nel secondo y2 -y1 = 0; ma sarebbe valida comunque la relazione (9') (y2 -y1)(x -x1) = (x2 -x1)( y -y1), ottenuta dalla (9).
Esempi
1)-Determinare l'equazione della retta r congiungente i punti P1(2, - 3) e P2(- 3, 1).
Essendo x1 = 2, x2 = - 3, y1 = - 3, y2 = 1, indicando con x ed y le coordinate di un punto generico della retta r e applicando la (9), si ha;
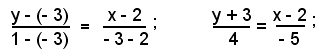
dopo facili calcoli, risulta
4x + 5y - 8 + 15 = 0,
ossia
4x + 5y + 7 =0.
Verifica: l'equazione 4x + 5y + 7 = 0 rappresenta la retta congiungente i punti P1 e P2, se le coordinate di P1 e P2 soddisfano l'equazione. Le coordinate di P1 sono x1 = 2, y1 = - 3, sostituendo 2 alla x e 3 alla y nell'equazione suddetta, si ha:
4 · 2 - 3 · 5 + 7 = 8 + -15 + 7 = 15 - 15 = 0.
Cioè (2, - 3) rappresenta una soluzione dell'equazione 4x + 5y + 7 = 0 e quindi P1 appartiene alla retta r. Procedendo allo stesso modo per P2(-3, 1), si ha:
4 · (-3) + 5 · 5(1) + 7 = - 12 + + 5 + 7 = 12 - 12 = 0.
Quindi anche P2 appartiene alla retta r.
2)-Determinare l'equazione della retta r congiungente i punti P1(-2, 3) e P2(- 2, 5).
Essendo x1 = - 2, x2 = - 2, y1 = 3, y2 = 5, indicando con x ed y le coordinate di un punto generico della retta r, applicando la (9), si ha;
espressione priva di significato perchè contiene zero al denominatore.
Per eliminare tale inconveniente, si applica la relazione (9') (y2 - y1)( x - x1) = (x2 - x1)( y - y1) e si ha:
(5 - 3)(x + 2) = 0(y - y1);
2(x + 2) = 0;
x + 2 = 0;
x = - 2
che rappresenta l'equazione della retta parallela all'asse y.
Nota bene
L'equazione della retta r congiungente i punti P1(-2, 3) e P2(- 2, 5), poteva determinarsi direttamente osservando che i punti P1 e P2 hanno la stessa ascissa, cioè la stessa distanza dall'asse y, e quindi devono appartenere alla retta di equazione x = - 2.
3)-Determinare l'equazione della retta r congiungente i punti P1(1, 4) e P2(3, 4).
Infatti, applicando la (9'), si ha:
0(x - x1) = (3 - 1)(y - 4);
0(x - x1) = (3 - 1)(y - 4);
0= 2(y - 4);
y - 4 = 0.
y = 4.
Fascio di rette
Si definisce fascio di rette la totalità delle rette passanti per un punto, detto centro del fascio.
Nota bene
Per totalità di rette passanti per un punto s'intende "infinite rette".
Si vuole determinare ora la sua equazione.
Sia ax + by + c = 0 l'equazione di una retta generica del piano e P(x0, y0) un punto.
Il punto P(x0, y0) apparterrà alla retta se e solo se le sue coordinate soddisferanno la relazione:
(10) ax0 + by0 + c =0.
La relazione (10) si chiama "condizione di appartenenza" del punto P(x0, y0) alla retta r.
Dalla (10) si ricava c = - ax0 - by0 e sostituendo tale valore nell'equazione della retta, si ricava:
ax + by - ax0 - by0 = 0,
(11) a(x - x0) + b(y - y0) = 0,
per a = 0, si avrà la retta del fascio parallela all'asse x di equazione y - y0 = 0;
per b = 0, si avrà la retta del fascio parallela all'asse y di equazione x - x0 = 0.
Al variare dei coefficienti a e b la retta ruota intorno al punto P descrivendo il fascio di centro P. Non potendo essere a e b simultaneamente nulli, la (11) dipende da un solo coefficiente essenziale.
Esempio
Determinare l'equazione del fascio di rette di centro P(1, 3).
Applicando la (11), si ha: a(x - 1) + b(y - 3) = 0.
Intersezione di due rette - Rette parallele
In un piano cartesiano, siano date le rette r e r', rispettivamente di equazioni:
ax + by + c = 0, a'x + b'y + c' = 0.
Si vogliono determinare le coordinate del punto P, intersezione di r con r'.
Poichè il punto P deve appartenere alla retta r, le sue coordinate devono soddisfare la prima equazione; poichè il punto P sta sulla retta r', le sue coordinate devono soddisfare la seconda equazione, quindi le coordinate di P sono la soluzione comune alla prima e alla seconda equazione, cioè rappresentano la "soluzione del sistema": a
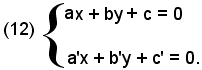
Quindi:
-per determinare le coordinate del punto di intersezione di due rette incidenti, si risolve il sistema formato dalle equazioni delle rette stesse.
Le rette r e r' sono incidenti, se il sistema (12) è determinato. Ciò si verifica, come è noto dall'algebra, se il determinante dei coefficienti delle incognite:
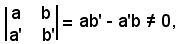
oppure
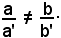
In tal caso il punto P, intersezione di r con r' avrà per coordinate le soluzioni del sistema (12), risolto con il metodo di Cramer:
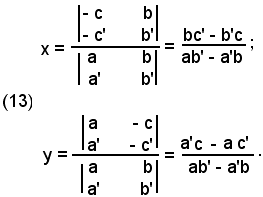
Le due rette r e r' sono parallele se il sistema (12) è impossibile e ciò si verifica se il determinante dei coefficienti delle incognite è uguale a zero, cioè:
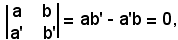
ossia
(14) a b' = a' b,
oppure dividendo la (14) per a' b',
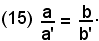
Ponendo:
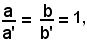
si ha
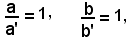
da cui
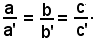
E precisamente, x ed y sono indeterminate quando:
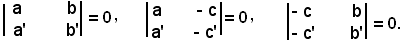
Dunque:
-condizione necessaria e sufficiente affinchè due equazioni di primo grado, nelle variabili x ed y rappresentino la stessa retta è che i coefficienti delle incognite siano proporzionali.
Esempi
1)-Determinare l'intersezione delle rette aventi equazioni x + y - 5 = 0 e 3x - y + 2 = 0.
Si risolve il sistema formato dalle due equazioni:
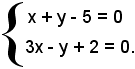
Le due rette sono incidenti, perchè il determinante dei coefficienti delle incognite è diverso da zero, precisamente:
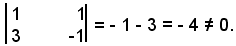
Risolvendo il sistema si trova:
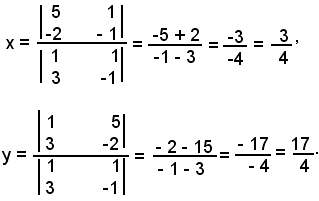
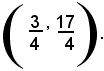
Quindi, le due rette s'incontrano nel punto di coordinate:
2)-Determinare l'intersezione delle rette aventi equazioni 4x - 10y + 1 = 0 e 2x - 5y + 3 = 0.
Le rette sono parallele perchè i coefficienti delle incognite sono proporzionali.
Infatti:
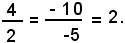
3)-Determinare l'intersezione delle rette aventi equazioni 2x - 3y + 5 = 0 e 4x - 6y + 10 = 0.
Le rette sono coincidenti perchè i coefficienti delle incognite ed i termini noti sono proporzionali.
Infatti:
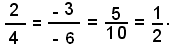
Problema - Retta per P(1, -2) parallela alla retta r di equazione 3x - 4y + 5 = 0.
Poichè la retta generica passa per il punto P, applicando:
a(x - x0) + b(y - y0) = 0,
si ha:
a(x - 1) + b(y - 2) = 0.
Siccome le due rette sono parallele, nelle loro equazioni i coefficienti delle incognite devono essere proporzionali oppure uguali, quindi a = 3 e b = - 4. Sostituendo tali valori nell'equazione precedente, si ha:
3 · 1 - 4(-2) + h = 0,
da cui
h = - 11.
Sostituendo tale valore nell'equazione del fascio, si ottiene:
3x - 4y - 11 = 0,
Verifica: la retta di equazione 3x - 4y - 11 = 0, è parallela alla retta 3x - 4y + 5 = 0, in quanto le rispettive equazioni differiscono del termine noto, e passa per P(1, -2) in quanto le coordinate soddisfano l'equazione.
Infatti:
3 · 1 - 4(-2) - 11 = 3 + 8 - 11 = 11 - 11 = 0.
Nota bene
L'insieme di tutte le rette parallele ad una retta data si chiama "fascio improprio di rette".
Intersezione di una retta con gli assi - Equazione segmentaria di una retta
Data la retta di equazione ax + by + c = 0, si vogliono determinare le coordinate dei punti M e N in cui la retta incontra rispettivamente gli assi x ed y. Le coordinate del punto M, intersezione di r con l'asse x si trovano risolvendo il sistema formato dalle equazioni di r e dell'asse x:
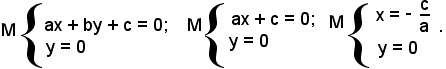
Posto:
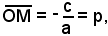
si ha che le coordinate di M sono (p, 0).
Nello stesso modo si procede per determinare le coordinate di N, risolvendo il sistema formato dalle equazioni di r e dell'asse y:
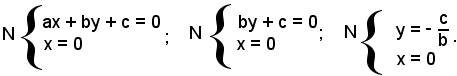
Posto:
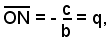
si ha che le coordinate di N sono (0, q).
p e q si chiamano intercette della retta sugli assi; esse rappresentano le misure dei segmenti intercettati dalla retta con gli assi, a partire dall'origine O.
Data l'equazione di una retta r, non passante per l'origine, la si può tracciare determinando direttamente le sue intercette:
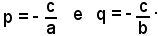
Viceversa, date le intercette della retta, si può scrivere direttamente la sua equazione nella forma: (18)
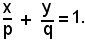
Infatti, la retta r congiungente i punti M e N, ha equazione:
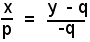
e, semplificando e ordinando, si ottiene: (18)
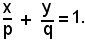
La (18) si chiama equazione segmentaria della retta.
La (17) non può applicarsi alle rette passanti per l'origine, in tal caso p = q = 0 oppure alle rette parallele all'asse x, p = ∞, oppure alle rette parallele all'asse u, q = ∞.
Esempi
1)-Disegnare la retta di equazione 3x + 2y - 6 = 0.
Si determinano le intercette della retta:
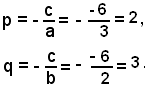
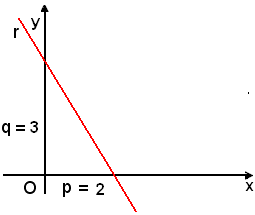
2)-Scrivere l'equazione della retta che stacca sugli assi, rispettivamente i segmenti p = 2, q =3. L'equazione della retta è:
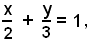
3x + 2y - 6 = 0.
Equazione della retta in forma ridotta o canonica
Si risolve rispetto ad y l'equazione della retta r ax + by + c = 0, supponendo b≠ 0, cioè la retta non parallela all'asse y.
Portando al secondo membro il primo e il terzo termine, si ha:
by = - ax - c;
dividendo per b ≠ 0, si ha:
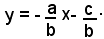
Posto:
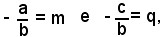
ove q è l'intercetta della retta sull'asse y, l'equazione precedente diventa:
(19) y = mx + q,
che perde di significato se la retta è parallela all'asse y. L'equazione (19) si chiama equazione "ridotta o canonica" della retta.
Il significato di m
Data la retta r di equazione y = mx + q, si consideri la parallela r' ad r passante per l'origine degli assi. La sua equazione è:
(20) y = m x.
Nota bene
Per totalità di rette passanti per un punto s'intende "infinite rette".
Si vuole determinare ora la sua equazione.
Sia ax + by + c = 0 l'equazione di una retta generica del piano e P(x0, y0) un punto.
Il punto P(x0, y0) apparterrà alla retta se e solo se le sue coordinate soddisferanno la relazione:
(10) ax0 + by0 + c =0.
La relazione (10) si chiama "condizione di appartenenza" del punto P(x0, y0) alla retta r.
Dalla (10) si ricava c = - ax0 - by0 e sostituendo tale valore nell'equazione della retta, si ricava:
ax + by - ax0 - by0 = 0,
(11) a(x - x0) + b(y - y0) = 0,
per a = 0, si avrà la retta del fascio parallela all'asse x di equazione y - y0 = 0;
per b = 0, si avrà la retta del fascio parallela all'asse y di equazione x - x0 = 0.
Al variare dei coefficienti a e b la retta ruota intorno al punto P descrivendo il fascio di centro P. Non potendo essere a e b simultaneamente nulli, la (11) dipende da un solo coefficiente essenziale.
Esempio
Determinare l'equazione del fascio di rette di centro P(1, 3).
Applicando la (11), si ha: a(x - 1) + b(y - 3) = 0.
Intersezione di due rette - Rette parallele
In un piano cartesiano, siano date le rette r e r', rispettivamente di equazioni:
ax + by + c = 0, a'x + b'y + c' = 0.
Si vogliono determinare le coordinate del punto P, intersezione di r con r'.
Poichè il punto P deve appartenere alla retta r, le sue coordinate devono soddisfare la prima equazione; poichè il punto P sta sulla retta r', le sue coordinate devono soddisfare la seconda equazione, quindi le coordinate di P sono la soluzione comune alla prima e alla seconda equazione, cioè rappresentano la "soluzione del sistema": a
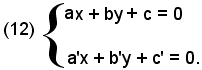
Quindi:
-per determinare le coordinate del punto di intersezione di due rette incidenti, si risolve il sistema formato dalle equazioni delle rette stesse.
Le rette r e r' sono incidenti, se il sistema (12) è determinato. Ciò si verifica, come è noto dall'algebra, se il determinante dei coefficienti delle incognite:
oppure
In tal caso il punto P, intersezione di r con r' avrà per coordinate le soluzioni del sistema (12), risolto con il metodo di Cramer:
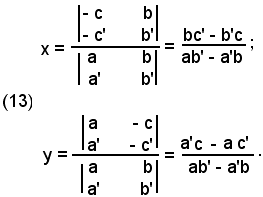
Le due rette r e r' sono parallele se il sistema (12) è impossibile e ciò si verifica se il determinante dei coefficienti delle incognite è uguale a zero, cioè:
ossia
(14) a b' = a' b,
oppure dividendo la (14) per a' b',
Ponendo:
si ha
da cui
(16) a = a', b = b'.
Le condizioni (15) e (16) si possono riassumere come segue:
-condizione necessaria e sufficiente affinchè due equazioni di primo grado, nelle variabili x ed y rappresentino due rette parallele è che i coefficienti delle incognite siano proporzionali oppure uguali.
In generale, la parallela alla retta ax + by + c = 0 per il punto P(x0, y0) ha equazione:
(16') a(x - x0) + b(y - y0) = 0.
Le rette r e r' sono coincidenti se il sistema (12) è indeterminato e ciò si verifica se: (17)
Le condizioni (15) e (16) si possono riassumere come segue:
-condizione necessaria e sufficiente affinchè due equazioni di primo grado, nelle variabili x ed y rappresentino due rette parallele è che i coefficienti delle incognite siano proporzionali oppure uguali.
In generale, la parallela alla retta ax + by + c = 0 per il punto P(x0, y0) ha equazione:
(16') a(x - x0) + b(y - y0) = 0.
Le rette r e r' sono coincidenti se il sistema (12) è indeterminato e ciò si verifica se: (17)
E precisamente, x ed y sono indeterminate quando:
Dunque:
-condizione necessaria e sufficiente affinchè due equazioni di primo grado, nelle variabili x ed y rappresentino la stessa retta è che i coefficienti delle incognite siano proporzionali.
Esempi
1)-Determinare l'intersezione delle rette aventi equazioni x + y - 5 = 0 e 3x - y + 2 = 0.
Si risolve il sistema formato dalle due equazioni:
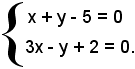
Le due rette sono incidenti, perchè il determinante dei coefficienti delle incognite è diverso da zero, precisamente:
Risolvendo il sistema si trova:
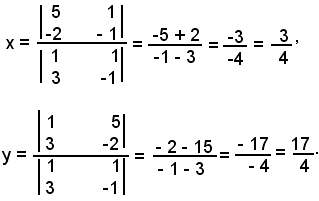
Quindi, le due rette s'incontrano nel punto di coordinate:
2)-Determinare l'intersezione delle rette aventi equazioni 4x - 10y + 1 = 0 e 2x - 5y + 3 = 0.
Le rette sono parallele perchè i coefficienti delle incognite sono proporzionali.
Infatti:
3)-Determinare l'intersezione delle rette aventi equazioni 2x - 3y + 5 = 0 e 4x - 6y + 10 = 0.
Le rette sono coincidenti perchè i coefficienti delle incognite ed i termini noti sono proporzionali.
Infatti:
Problema - Retta per P(1, -2) parallela alla retta r di equazione 3x - 4y + 5 = 0.
Poichè la retta generica passa per il punto P, applicando:
si ha:
Siccome le due rette sono parallele, nelle loro equazioni i coefficienti delle incognite devono essere proporzionali oppure uguali, quindi a = 3 e b = - 4. Sostituendo tali valori nell'equazione precedente, si ha:
3(x - 1) - 4(y - 2) = 0,
ossia
3x - 4y - 11 = 0,
che è l'equazione della retta richiesta dal problema.
Si poteva pervenire al risultato anche con il seguente procedimento: è noto che due rette sono parallele quando le rispettive equazioni differiscono del termine noto, cioè
3x - 4 y + h = 0,
sarà l'equazione delle infinite parallele alla retta r.
La generica retta 3x - 4y + h = 0, passa per il punto P(1, - 2), se le coordinate di P soddisfano l'equazione, per cui si ha:ossia
che è l'equazione della retta richiesta dal problema.
Si poteva pervenire al risultato anche con il seguente procedimento: è noto che due rette sono parallele quando le rispettive equazioni differiscono del termine noto, cioè
3x - 4 y + h = 0,
sarà l'equazione delle infinite parallele alla retta r.
3 · 1 - 4(-2) + h = 0,
da cui
h = - 11.
Sostituendo tale valore nell'equazione del fascio, si ottiene:
3x - 4y - 11 = 0,
Verifica: la retta di equazione 3x - 4y - 11 = 0, è parallela alla retta 3x - 4y + 5 = 0, in quanto le rispettive equazioni differiscono del termine noto, e passa per P(1, -2) in quanto le coordinate soddisfano l'equazione.
Infatti:
Nota bene
L'insieme di tutte le rette parallele ad una retta data si chiama "fascio improprio di rette".
Intersezione di una retta con gli assi - Equazione segmentaria di una retta
Data la retta di equazione ax + by + c = 0, si vogliono determinare le coordinate dei punti M e N in cui la retta incontra rispettivamente gli assi x ed y. Le coordinate del punto M, intersezione di r con l'asse x si trovano risolvendo il sistema formato dalle equazioni di r e dell'asse x:
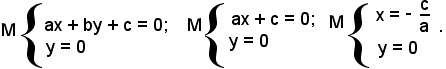
Posto:
si ha che le coordinate di M sono (p, 0).
Nello stesso modo si procede per determinare le coordinate di N, risolvendo il sistema formato dalle equazioni di r e dell'asse y:
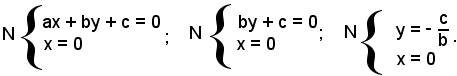
Posto:
si ha che le coordinate di N sono (0, q).
p e q si chiamano intercette della retta sugli assi; esse rappresentano le misure dei segmenti intercettati dalla retta con gli assi, a partire dall'origine O.
Data l'equazione di una retta r, non passante per l'origine, la si può tracciare determinando direttamente le sue intercette:
Viceversa, date le intercette della retta, si può scrivere direttamente la sua equazione nella forma: (18)
Infatti, la retta r congiungente i punti M e N, ha equazione:
e, semplificando e ordinando, si ottiene: (18)
La (18) si chiama equazione segmentaria della retta.
La (17) non può applicarsi alle rette passanti per l'origine, in tal caso p = q = 0 oppure alle rette parallele all'asse x, p = ∞, oppure alle rette parallele all'asse u, q = ∞.
Esempi
1)-Disegnare la retta di equazione 3x + 2y - 6 = 0.
Si determinano le intercette della retta:
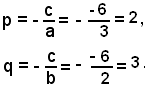
2)-Scrivere l'equazione della retta che stacca sugli assi, rispettivamente i segmenti p = 2, q =3. L'equazione della retta è:
3x + 2y - 6 = 0.
Equazione della retta in forma ridotta o canonica
Si risolve rispetto ad y l'equazione della retta r ax + by + c = 0, supponendo b≠ 0, cioè la retta non parallela all'asse y.
Portando al secondo membro il primo e il terzo termine, si ha:
dividendo per b ≠ 0, si ha:
Posto:
ove q è l'intercetta della retta sull'asse y, l'equazione precedente diventa:
(19) y = mx + q,
che perde di significato se la retta è parallela all'asse y. L'equazione (19) si chiama equazione "ridotta o canonica" della retta.
Il significato di m
Data la retta r di equazione y = mx + q, si consideri la parallela r' ad r passante per l'origine degli assi. La sua equazione è:
(20) y = m x.
Nota bene
Si deve ricordare che una retta r' passa per l'origine degli assi quando nella sua equazione manca il termine noto, mentre è parallela ad r quando i coefficienti della incognite sono uguali.
Sia P, un punto di ascissa x ed ordinata y, generico della retta r, e si indichi con α l'angolo che essa forma con l'asse x, cioè l'angolo di cui deve ruotare il semiasse positivo x intorno all'origine, in senso antiorario, per sovrapporsi alla retta. Dal triangolo rettangolo OMP, per un noto teorema di trigonometria, risulta:
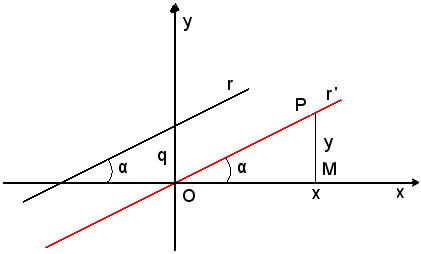
cioè
(21) y = tg α · x.
Le (20) e (21) rappresentano la stessa retta r' quando e solo quando i loro coefficienti sono proporzionali, ossia si verifichi:
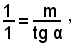
da cui
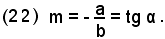
Il numero m si chiama "coefficiente angolare o coefficiente direttivo della retta".
Esso rappresenta:
-la tangente trigonometrica dell'angolo che il semiasse positivo delle x forma con la retta.
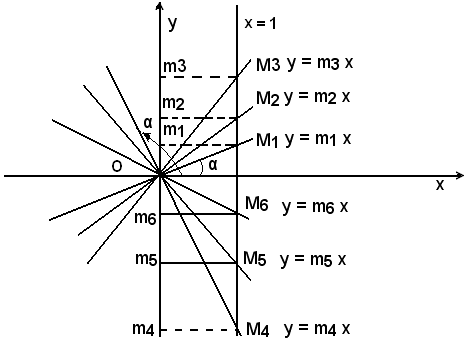
Coefficiente angolare di una retta individuata mediante due punti
Sia data la retta r individuata da due suoi punti P1(x1, y1) e P2 (x2, y2); si vuole calcolare il coefficiente angolare senza scrivere l'equazione. Si conduce per P2 la parallela all'asse y e per P1 la parallela all'asse x e sia M il loro punto d'intersezione. Il coefficiente angolare della retta r è "la tangente dell'angolo α" che la retta forma con l'asse x, cioè l'angolo P2 P1 M. Dal triangolo P2 P1 M si ha:
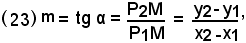
cioè il coefficiente angolare di una retta che passa per due punti è uguale al rapporto fra la differenza delle ordinate e la differenza della ascisse dei due punti.
Esempio
Il coefficiente angolare della retta congiungente i punti A(3, 1) e B(-2, 5) è dato da:
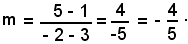
Fascio di rette
Retta di un dato coefficiente angolare per un punto
Spesso è utile scrivere l'equazione di una retta passante per un punto quando si vuole evidenziare il coefficiente angolare.
Risolvendo l'equazione a(x - x0) + b(y - y0) = 0 rispetto a y - y0, si ha:
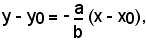
ed essendo
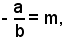
si ottiene
(24) y - y0 = m(x - x0)
Al variare di m la (24) fornisce l'equazione del fascio di rette di centro P(x0, y0), cioè le infinite rette passanti per il punto P(x0, y0).
Esempio
Determinare l'equazione della retta che passa per il punto A(1, 3) ed ha per coefficiente angolare m = 4/3.
Applicando la (24), si ha:
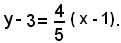
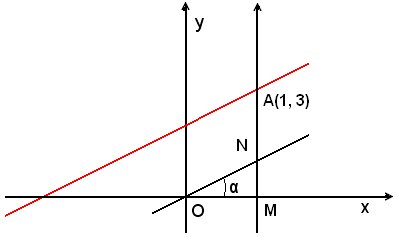
Assegnando arbitrariamente almeno due valori alla x, si avranno altrettanti valori della y e quindi si può tracciare la retta.
Operando in modo diverso, si può costruire l'angolo α avente per tangente 4/5, la retta per A(1, 3) avente tg α = m = 4/5 è la retta richiesta.
Allo scopo, si riporti sul semiasse positivo delle x un segmento unitario
sulla perpendicolare in M all'asse x, orientata dal basso verso l'alto, si prenda il segmento 
l'angolo 
ha per tangente 4/5. La parallela per A(1, 3) alla retta ON è la retta richiesta.
Condizione di parallelismo fra due rette le cui equazioni siano in forma ridotta
Siano r e r' due rette rispettivamente di equazioni:
y = mx + q, y = m'x + q'.
Dalla geometria elementare è noto che due rette sono fra loro parallele quando, tagliate da una trasversale, formano angoli corrispondenti uguali.
Nel piano cartesiano le due rette r e r', essendo parallele, formano con l'asse x angoli uguali. Le tangenti di tali angoli rappresentano, come è noto, i corfficienti angolari, m e m', delle rette e poichè le tangenti di angoli uguali sono uguali, si ha:
(25) m = m'.
La relazione (25) si poteva ricavare direttamente dalla
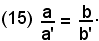
Infatti, permutando i medi, si può scrivere:
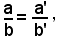
ossia
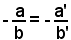
ed essendo
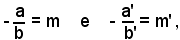
si ottiene:
m = m'.
Si può quindi affermare che:
-due rette sono parallele quando hanno coefficienti angolari uguali.
In generale, la parallela alla retta y = mx + q per P(x0, y0) ha equazione:
(26) y - y0 = m(x - x0).
Esempio
Retta r per P(1, 3) parallela alla retta y = 5x - 3.
Una qualsiasi parallela alla retta r deve avere lo stesso coefficiente angolare; l'equazione:
y = 5x + h
rappresenta il fascio improprio di rette, le infinite rette parallele alla retta r.
Si deve ricordare che una retta r' passa per l'origine degli assi quando nella sua equazione manca il termine noto, mentre è parallela ad r quando i coefficienti della incognite sono uguali.
Sia P, un punto di ascissa x ed ordinata y, generico della retta r, e si indichi con α l'angolo che essa forma con l'asse x, cioè l'angolo di cui deve ruotare il semiasse positivo x intorno all'origine, in senso antiorario, per sovrapporsi alla retta. Dal triangolo rettangolo OMP, per un noto teorema di trigonometria, risulta:
cioè
(21) y = tg α · x.
Le (20) e (21) rappresentano la stessa retta r' quando e solo quando i loro coefficienti sono proporzionali, ossia si verifichi:
da cui
Il numero m si chiama "coefficiente angolare o coefficiente direttivo della retta".
Esso rappresenta:
-la tangente trigonometrica dell'angolo che il semiasse positivo delle x forma con la retta.
Nota bene
Il noto teorema di trigonometria esprime che: "in un triangolo rettangolo un cateto è uguale all'altro cateto per la tangente dell'angolo opposto (al primo cateto).
Si ricordi inoltre che se l'equazione della retta è data nella forma ax + by + c = 0, il coefficiente angolare m è fornito dal coefficiente della x cambiato di segno, diviso il coefficiente dalla y.
Il noto teorema di trigonometria esprime che: "in un triangolo rettangolo un cateto è uguale all'altro cateto per la tangente dell'angolo opposto (al primo cateto).
Si ricordi inoltre che se l'equazione della retta è data nella forma ax + by + c = 0, il coefficiente angolare m è fornito dal coefficiente della x cambiato di segno, diviso il coefficiente dalla y.
Se
non si è in grado di applicare le regole dettate dalla
trigonometria, si può rilevare la relazione esistente fra m e
l'angolo α nel modo
seguente: si considera un fascio di rette avente il centro nell'origine
O e le ordinate dei punti d'intersezione delle rette del fascio con la
retta di equazione x = 1. Si rileva che al variare di m, varia l'angolo
che la retta forma con il semiasse positivo delle x. Si osserva che: se
m è positivo, l'angolo α è acuto e i punti della retta appartengono al I e III quadrante; se m è negativo l'angolo α è ottuso e i punti della retta appartengono al II e IV quadrante.
Coefficiente angolare di una retta individuata mediante due punti
Sia data la retta r individuata da due suoi punti P1(x1, y1) e P2 (x2, y2); si vuole calcolare il coefficiente angolare senza scrivere l'equazione. Si conduce per P2 la parallela all'asse y e per P1 la parallela all'asse x e sia M il loro punto d'intersezione. Il coefficiente angolare della retta r è "la tangente dell'angolo α" che la retta forma con l'asse x, cioè l'angolo P2 P1 M. Dal triangolo P2 P1 M si ha:
cioè il coefficiente angolare di una retta che passa per due punti è uguale al rapporto fra la differenza delle ordinate e la differenza della ascisse dei due punti.
Esempio
Il coefficiente angolare della retta congiungente i punti A(3, 1) e B(-2, 5) è dato da:
Fascio di rette
Retta di un dato coefficiente angolare per un punto
Spesso è utile scrivere l'equazione di una retta passante per un punto quando si vuole evidenziare il coefficiente angolare.
Risolvendo l'equazione a(x - x0) + b(y - y0) = 0 rispetto a y - y0, si ha:
ed essendo
si ottiene
(24) y - y0 = m(x - x0)
Al variare di m la (24) fornisce l'equazione del fascio di rette di centro P(x0, y0), cioè le infinite rette passanti per il punto P(x0, y0).
Esempio
Determinare l'equazione della retta che passa per il punto A(1, 3) ed ha per coefficiente angolare m = 4/3.
Applicando la (24), si ha:
Assegnando arbitrariamente almeno due valori alla x, si avranno altrettanti valori della y e quindi si può tracciare la retta.
Operando in modo diverso, si può costruire l'angolo α avente per tangente 4/5, la retta per A(1, 3) avente tg α = m = 4/5 è la retta richiesta.
Allo scopo, si riporti sul semiasse positivo delle x un segmento unitario
sulla perpendicolare in M all'asse x, orientata dal basso verso l'alto, si prenda il segmento l'angolo ha per tangente 4/5. La parallela per A(1, 3) alla retta ON è la retta richiesta.Condizione di parallelismo fra due rette le cui equazioni siano in forma ridotta
Siano r e r' due rette rispettivamente di equazioni:
y = mx + q, y = m'x + q'.
Dalla geometria elementare è noto che due rette sono fra loro parallele quando, tagliate da una trasversale, formano angoli corrispondenti uguali.
Nel piano cartesiano le due rette r e r', essendo parallele, formano con l'asse x angoli uguali. Le tangenti di tali angoli rappresentano, come è noto, i corfficienti angolari, m e m', delle rette e poichè le tangenti di angoli uguali sono uguali, si ha:
(25) m = m'.
La relazione (25) si poteva ricavare direttamente dalla
Infatti, permutando i medi, si può scrivere:
ossia
ed essendo
si ottiene:
Si può quindi affermare che:
-due rette sono parallele quando hanno coefficienti angolari uguali.
In generale, la parallela alla retta y = mx + q per P(x0, y0) ha equazione:
(26) y - y0 = m(x - x0).
Esempio
Retta r per P(1, 3) parallela alla retta y = 5x - 3.
Una qualsiasi parallela alla retta r deve avere lo stesso coefficiente angolare; l'equazione:
y = 5x + h
rappresenta il fascio improprio di rette, le infinite rette parallele alla retta r.
La retta di equazione, y = 5x + h passerà per P se le coordinate di P soddisfano l'equazione, cioè se si verifica la condizione
da cui
y = 5x - 2,
che è l'equazione della retta richiesta.
Oppure:
la retta generica per P(1, 3) ha equazione:
y - 3 = m(x - 1).
Tale retta è parallela alla retta data, se ha il coefficiente angolare uguale a quello dalla retta r, cioè:
m = 5.
Quindi la retta richiesta ha equazione:
y - 3 = 5(x - 1),
ossia
y = 5x - 2.
Rette perpendicolari
Siano r e r' due rette di equazioni rispettivamente:
y = mx + q e y = m'x + q'.
Se r e r' sono perpendicolari, altrettanto avverrà per qualsiasi coppia di rette ad esse parallele e condotte per un qualsiasi punto del piano. In particolare saranno perpendicolari le rette s1 e s2 di equazioni y = mx e y = m'x parallele alle rette date e passanti per l'origine.
Supposto che le rette s1 e s2 non siano parallele agli assi, siano S, M, N le intersezioni della x = 1, rispettivamente con l'asse x e con le rette s1 e s2.
Si osservi che i punti M ed N giacciono da bande opposte rispetto all'asse x, cioè le ordinate
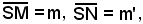
rispettivamente di M, N, sono discordi.
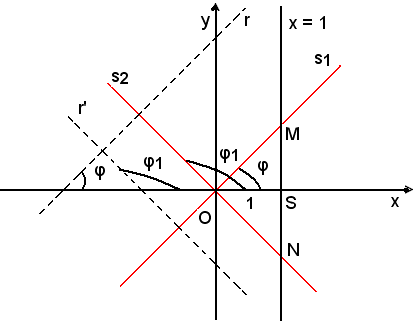
Si ricorda il secondo teorema di Euclide "in un triangolo rettangolo l'altezza relativa all'ipotenusa è media proporzionale fra le proiezioni dei cateti sulla stessa ipotenusa" e lo si applica al triangolo rettangolo NOM, di ipotenusa NM e di altezza relativa ad essa OS = 1, si ottiene:
ossia
|m| · |m'| = - 1
e poichè, come si è osservato m e m' sono discordi, risulta
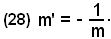
Si può quindi affermare che:
-i coefficienti angolari di due rette perpendicolari sono opposti e reciproci.
La (28) si può dimostrare anche nel modo seguente: siano φ1 e φ2 gli angoli che le rette s1 e s2 formano con l'asse x, si rileva che:
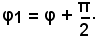
Prendendo la tangente di ambo i membri e ricordando che:
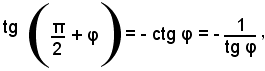
si ha
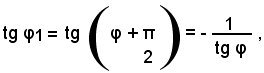
ed essendo
tg φ = m e tg φ1 = m',
si ha
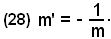
In conclusione, l'equazione di una retta generica perpendicolare alla retta di equazione y =mx + q, è del tipo:
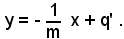
Se le rette r e r' sono date rispettivamente dalle equazioni ax + by è c = 0 e a'x + b'y + c' =0, ricordando che
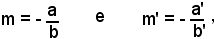
la (28) si trasforma in
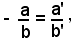
ossia
(29) aa' + bb' =0
ossia
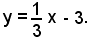
Angolo di due retteSiano a e b due rette orientate, che s'incontrano nel punto P:
-si chiama angolo
"l'angolo minore di 2 π radianti, o 360°" di cui deve ruotare intorno a P in senso antiorario la retta a per sovrapporsi alla retta b.
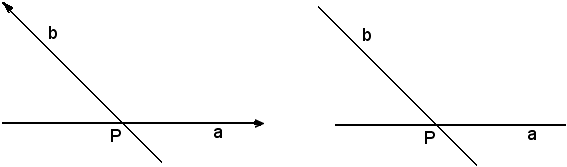
Si chiama angolo ab di due rette a e b incidenti in P non orientate "l'angolo minore di π radianti, o 180°" di cui deve ruotare intorno a P in senso antiorario la retta a per sovrapporsi alla retta b.
Si noti la differenza fra le due definizioni: essa si comprende considerando il fatto che, per sovrapporre a se stessa una retta orientata bisogna farla ruotare di un angolo giro, per sovraporre una retta non orientata basta farla ruotare di un angolo piatto.
Siano r e r' due rette di equazioni rispettivamente:
y ) mx + q e y = m'x + q';
si vuole determinare la tangente trigonometrica dell'angolo ω formato dalle due rette, mediante i coefficienti angolari delle equazioni di r e r'.
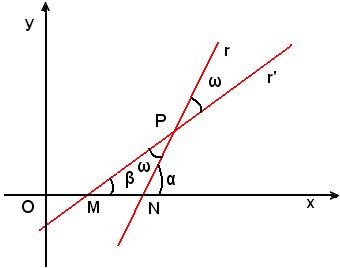
Dalla figura si rileva che: α, angolo esterno del triangolo MNP, è uguale alla somma degli angoli interni non adiacenti del triangolo, cioè:
α = β + ω,
da cui
ω = α - β.
Si ricorda ora che la relazione esistente fra la misura di un angolo in radianti, αr, e quella, α°, in gradi sessagesimali è:
αr : α° = π : 180°,
cioè ricordando che il valore approssimato di π è 3,1415..., risulta
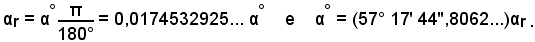
Poichè le tangenti di due angoli uguali, o differenti di π, sono uguali in valore e segno, mentre seno e coseno di due angoli che differiscono di π, sono uguali in valore assoluto ed opposti di segno, si ha:
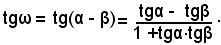
Ricordando che tgα = m e tgβ = m', si ha:
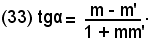
Volendo determinare il seno e il coseno dell'angolo ω, si ricordano le note formule di goniometria:
Così si ha:
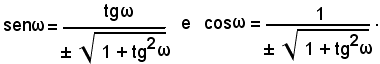
Sostituendo a tgω il valore espresso dalla (33), risulta:
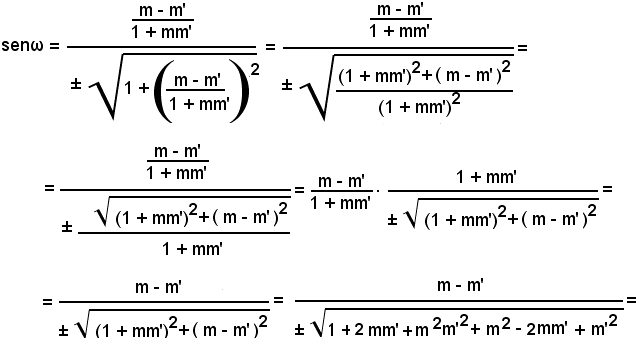
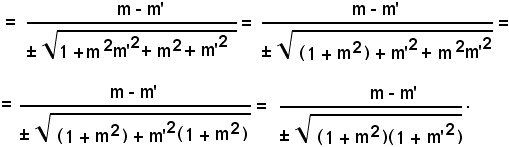
Quindi:
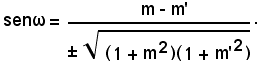
Per il coseno di ω, dopo semplicazioni, si ha:
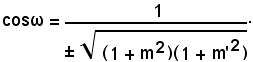
Se le equazioni delle rette r e r' sono rispettivamente ax + bx + c = 0 e a'x + b'y + c' =0, si ha:
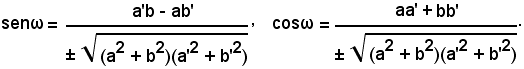
Poichè:
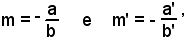
la (33) si trasforma in
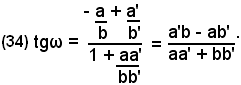
Se il numeratore m - m' della (33), o a'b - ab' della (34) è nullo, l'angolo ω è uguale a zero e le due rette sono parallele, perchè risulta m = m', oppure se a'b - ab'= 0 risulta a'b = ab'.
Nota bene
E' stato visto in precedenza che m = m', oppure a'b = ab' sono le condizioni di parallelismo fra due rette.
Se il denominatore 1 + mm' della (33) o aa' + bb' della (34) è nullo, l'angolo ω è uguale a π/2 e le due rette sono perpendicolari, perchè risulta 1 + mm' = 0, oppure se aa' - bb'= 0.
Nota bene
3 = 5 · 1 + h,
da cui
h = 3 - 5 = - 2
e sostituendo tale valore nella
e sostituendo tale valore nella
y = 5x + h,
si ha
y = 5x - 2,
che è l'equazione della retta richiesta.
Oppure:
la retta generica per P(1, 3) ha equazione:
y - 3 = m(x - 1).
Tale retta è parallela alla retta data, se ha il coefficiente angolare uguale a quello dalla retta r, cioè:
m = 5.
Quindi la retta richiesta ha equazione:
y - 3 = 5(x - 1),
ossia
y = 5x - 2.
Rette perpendicolari
Siano r e r' due rette di equazioni rispettivamente:
y = mx + q e y = m'x + q'.
Se r e r' sono perpendicolari, altrettanto avverrà per qualsiasi coppia di rette ad esse parallele e condotte per un qualsiasi punto del piano. In particolare saranno perpendicolari le rette s1 e s2 di equazioni y = mx e y = m'x parallele alle rette date e passanti per l'origine.
Supposto che le rette s1 e s2 non siano parallele agli assi, siano S, M, N le intersezioni della x = 1, rispettivamente con l'asse x e con le rette s1 e s2.
Si osservi che i punti M ed N giacciono da bande opposte rispetto all'asse x, cioè le ordinate
rispettivamente di M, N, sono discordi.
Si ricorda il secondo teorema di Euclide "in un triangolo rettangolo l'altezza relativa all'ipotenusa è media proporzionale fra le proiezioni dei cateti sulla stessa ipotenusa" e lo si applica al triangolo rettangolo NOM, di ipotenusa NM e di altezza relativa ad essa OS = 1, si ottiene:
ossia
e poichè, come si è osservato m e m' sono discordi, risulta
Si può quindi affermare che:
-i coefficienti angolari di due rette perpendicolari sono opposti e reciproci.
La (28) si può dimostrare anche nel modo seguente: siano φ1 e φ2 gli angoli che le rette s1 e s2 formano con l'asse x, si rileva che:
Prendendo la tangente di ambo i membri e ricordando che:
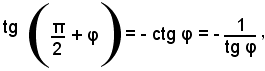
si ha
ed essendo
tg φ = m e tg φ1 = m',
si ha
In conclusione, l'equazione di una retta generica perpendicolare alla retta di equazione y =mx + q, è del tipo:
Se le rette r e r' sono date rispettivamente dalle equazioni ax + by è c = 0 e a'x + b'y + c' =0, ricordando che
la (28) si trasforma in
ossia
(29) aa' + bb' =0
Si può quindi affermare che:
-due rette sono perpendicolari quando la somma dei prodotti dei coefficienti delle incognite omonime è uguale a zero.
La (29), data l'equazione di una retta ax + by + c = 0, permette di scrivere l'equazione di una retta perpendicolare alla data; essa è del tipo:
(30) bx - ay + h =0.
Cioè:
-i coefficienti dell'equazione della perpendicolare ad una retta data sono i coefficienti dell'equazione della stessa retta scambiati fra loro, ed uno cambiato di segno.
In generale, la perpendicolare alla retta ax + by + c = 0 per il punto P(x0, y0) ha equazione:
(31) b(y - y0) = 0. a(y - y0) = 0.
Se l'equazione della retta è della forma y = mx + q, la perpendicolare ad essa per P(x0, y0) ha equazione:
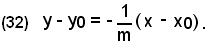
Retta per un punto perpendicolare a una retta data
Esempi
1)-Scrivere l'equazione della retta perpendicolare alla retta 3x + 2y - 6 = 0 passante per il punto P(1, 3).
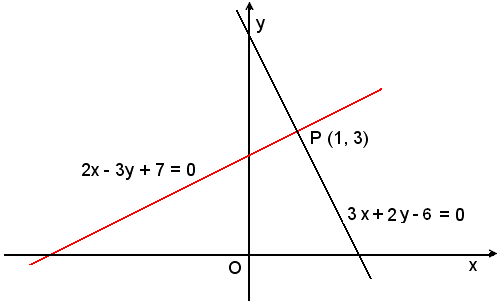
Una generica perpendicolare alla retta data, come si è visto, ha equazione:
2x - 3y + 7 = 0.
Tale retta passa per il punto P(1, 3) se le coordinate x0 e y0 rappresentano una soluzione dell'equazione, cioè se si verifica
2 · 1 - 3 · 3 + h = 0,
da cui
h = 7.
2x - 3y + 7 = 0,
della retta richiesta.
Più rapidamente, si poteva determinare l'equazione della retta richiesta applicando direttamente la (31), ottenendo:
2(x - 1) - 3(y - 3) = 0,
ossia
2x - 3y + 7 = 0.
2)-Dati il punto P(0, -3) e la retta r di equazione y = -3x + 6, scrivere l'equazione della retta che esce da P perpendicolare alla retta r.
Una generica perpendicolare alla retta data, come è noto ha equazione:
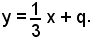
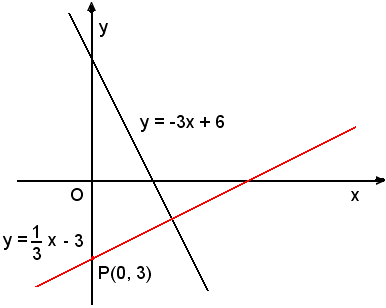
Tale retta passa per P(0, 3) se e solo se le coordinate di P sooddisfano l'equazione cioè se si verifica che:
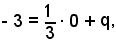
da cui
q = -3.
Sostituendo il valore di q nell'equazione suddetta, si ha:
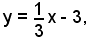
-due rette sono perpendicolari quando la somma dei prodotti dei coefficienti delle incognite omonime è uguale a zero.
La (29), data l'equazione di una retta ax + by + c = 0, permette di scrivere l'equazione di una retta perpendicolare alla data; essa è del tipo:
(30) bx - ay + h =0.
Cioè:
-i coefficienti dell'equazione della perpendicolare ad una retta data sono i coefficienti dell'equazione della stessa retta scambiati fra loro, ed uno cambiato di segno.
In generale, la perpendicolare alla retta ax + by + c = 0 per il punto P(x0, y0) ha equazione:
(31) b(y - y0) = 0. a(y - y0) = 0.
Se l'equazione della retta è della forma y = mx + q, la perpendicolare ad essa per P(x0, y0) ha equazione:
Retta per un punto perpendicolare a una retta data
Esempi
1)-Scrivere l'equazione della retta perpendicolare alla retta 3x + 2y - 6 = 0 passante per il punto P(1, 3).
Una generica perpendicolare alla retta data, come si è visto, ha equazione:
2x - 3y + 7 = 0.
Tale retta passa per il punto P(1, 3) se le coordinate x0 e y0 rappresentano una soluzione dell'equazione, cioè se si verifica
2 · 1 - 3 · 3 + h = 0,
da cui
h = 7.
Tale valore, sostituito in
dà l'equazione
2x - 3y + h =0,
dà l'equazione
2x - 3y + 7 = 0,
della retta richiesta.
Più rapidamente, si poteva determinare l'equazione della retta richiesta applicando direttamente la (31), ottenendo:
ossia
2)-Dati il punto P(0, -3) e la retta r di equazione y = -3x + 6, scrivere l'equazione della retta che esce da P perpendicolare alla retta r.
Una generica perpendicolare alla retta data, come è noto ha equazione:
Tale retta passa per P(0, 3) se e solo se le coordinate di P sooddisfano l'equazione cioè se si verifica che:
da cui
q = -3.
Sostituendo il valore di q nell'equazione suddetta, si ha:
l'equazione della retta richiesta.
L'equazione della retta richiesta poteva ottenersi applicando direttamente la (32) e ottenendo:
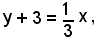
L'equazione della retta richiesta poteva ottenersi applicando direttamente la (32) e ottenendo:
ossia
Angolo di due rette
-si chiama angolo
"l'angolo minore di 2 π radianti, o 360°" di cui deve ruotare intorno a P in senso antiorario la retta a per sovrapporsi alla retta b.Si chiama angolo ab di due rette a e b incidenti in P non orientate "l'angolo minore di π radianti, o 180°" di cui deve ruotare intorno a P in senso antiorario la retta a per sovrapporsi alla retta b.
Si noti la differenza fra le due definizioni: essa si comprende considerando il fatto che, per sovrapporre a se stessa una retta orientata bisogna farla ruotare di un angolo giro, per sovraporre una retta non orientata basta farla ruotare di un angolo piatto.
Siano r e r' due rette di equazioni rispettivamente:
y ) mx + q e y = m'x + q';
si vuole determinare la tangente trigonometrica dell'angolo ω formato dalle due rette, mediante i coefficienti angolari delle equazioni di r e r'.
Dalla figura si rileva che: α, angolo esterno del triangolo MNP, è uguale alla somma degli angoli interni non adiacenti del triangolo, cioè:
da cui
Si ricorda ora che la relazione esistente fra la misura di un angolo in radianti, αr, e quella, α°, in gradi sessagesimali è:
αr : α° = π : 180°,
cioè ricordando che il valore approssimato di π è 3,1415..., risulta
Poichè le tangenti di due angoli uguali, o differenti di π, sono uguali in valore e segno, mentre seno e coseno di due angoli che differiscono di π, sono uguali in valore assoluto ed opposti di segno, si ha:
Ricordando che tgα = m e tgβ = m', si ha:
Volendo determinare il seno e il coseno dell'angolo ω, si ricordano le note formule di goniometria:
Così si ha:
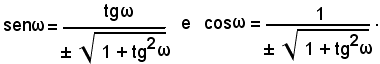
Sostituendo a tgω il valore espresso dalla (33), risulta:
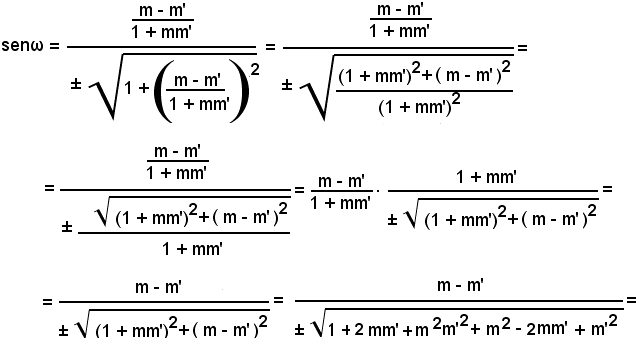
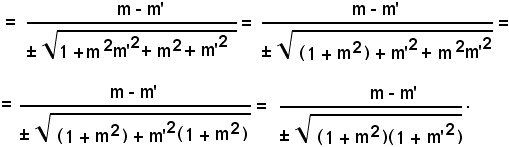
Quindi:
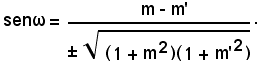
Per il coseno di ω, dopo semplicazioni, si ha:
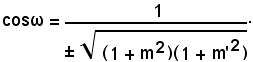
Se le equazioni delle rette r e r' sono rispettivamente ax + bx + c = 0 e a'x + b'y + c' =0, si ha:
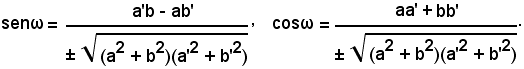
Poichè:
la (33) si trasforma in
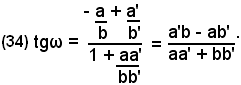
Se il numeratore m - m' della (33), o a'b - ab' della (34) è nullo, l'angolo ω è uguale a zero e le due rette sono parallele, perchè risulta m = m', oppure se a'b - ab'= 0 risulta a'b = ab'.
Nota bene
E' stato visto in precedenza che m = m', oppure a'b = ab' sono le condizioni di parallelismo fra due rette.
Se il denominatore 1 + mm' della (33) o aa' + bb' della (34) è nullo, l'angolo ω è uguale a π/2 e le due rette sono perpendicolari, perchè risulta 1 + mm' = 0, oppure se aa' - bb'= 0.
Nota bene
E' stato visto in precedenza che 1 + mm' = 0, oppure aa' - bb'= 0 sono le condizioni di perpendicolarità fra due rette.
E' bene ricordare che:
Quando s'impone che il denominatore della (33) o della (34) sia uguale a zero, si ha una frazione con il denominatore nullo, che è priva di significato ma in geometria analitica si usa chiamare infinita una frazione con denominatore nullo e numeratore diverso da zero, indeterminata se numeratore e denominatore sono nulli. Si suole anche affermare "condizione necessaria perchè una frazione sia infinite è che il suo numeratore sia uguale a zero."
Esempi
1)-Trovare la tangente, il seno e il coseno dell'angolo ω formato dalle seguenti rette:
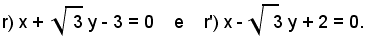
Essendo:
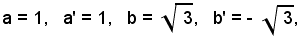
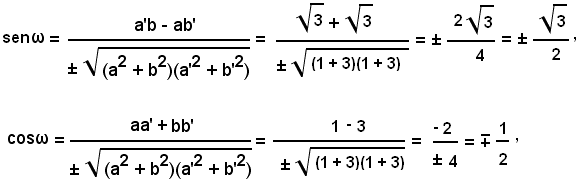
poichè è stato determinato
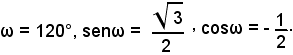
2)-Calcolare gli angoli del triangolo di vertici A(1, 2), B(-2, -3) C(3, -3).
Ricordando che il coefficiente angolare di una retta individuata mediante due punti P1(x1, y1) e P2(x2, y2) è dato dalla relazione (23), cioè da:
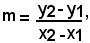
applicando la formula in tale caso, si trovano i coefficienti angolari m1, m2 , m3, rispettivamente delle rette AB, BC, CA:
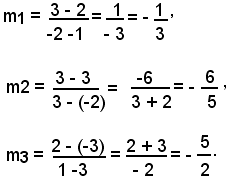
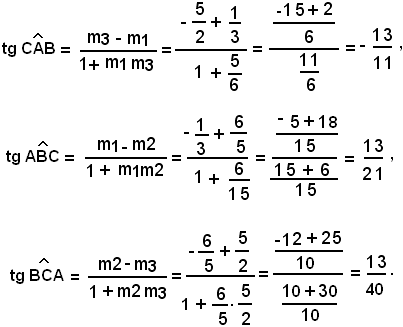
Da tali formule risulta:
Quindi, essendo noti i valori delle tangenti degli angoli, in corrispondenza di essi, si rileva dalle tavole il valore dei rispettivi angoli; essi sono:
Distanza di un punto da una retta
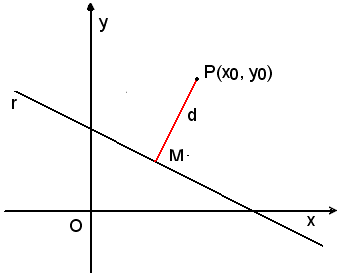
Data la retta r di equazione ax + by + c = 0 e un punto P(x0, y0) del piano, si definisce distanza del punto P dalla retta r la misura in valore assoluto del segmento di perpendicolare condotta dal punto alla retta data.
L'equazione della perpendicolare alla retta r per P, come è noto, è data da:
b(x - x0) - a(y - y0) = 0 .
Le coordinate di M, punto d'intersezione della retta r con la retta perpendicolare, sono fornite dalla soluzione del sistema:
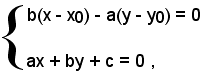
cioè
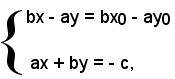
ossia
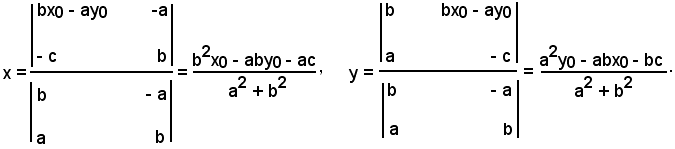
La distanza dei due punti P e M, fornisce la distanza di P dalla retta.
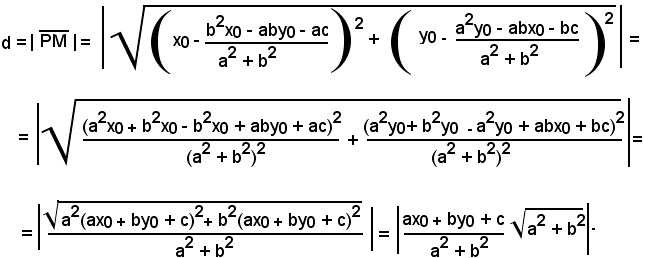
Quindi:
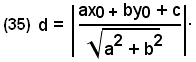
Si può affermare che:
-la distanza di un punto P(x0, y0) dalla retta ax + by + c = 0 è data in valore assoluto dal rapporto fra il valore che assume il primo membro dell'equazione della retta quando alle variabili x ed y si sostituiscono rispettivamente le coordinate x0 e y0 del punto e la radice quadrata della somma dei quadrati dei coefficienti di x e y dell'equazione della stessa retta.
Il segno di d è determinato quando è fissato il verso positivo di r.
Si osserva che la retta r divide il piano in due semipiani, punti appartenenti ad uno stesso semipiano hanno da r distanze dello stesso segno, precisamente, per una retta orientata, d è positiva per i punto che si trovano a sinistra di r rispetto ad un osservatore che percorre la retta nel senso positivo e d è negativo per quelli situati a destra.
Per una retta non orientata, si osserva che i due semipiani che la retta determina, sono caratterizzati dal fatto che le coordinate dei punto di uno rendono positivo il polinomio ax + by + c, primo membro dell'equazione della retta, e i punti dell'altro lo rendono negativo.
E' chiaro che, per passare da un punto del primo ad un punto del secondo, bisogna attraversare la retta. Convenzionalmente si può dire che i punti del semipiano che rendono positivo il polinomio ax + by + c hanno distanza positiva da r, di equazione ax + by + c = 0, mentre quelli che lo rendono negativo hanno distanza negativa.
Se il punto P(x0, y0) coincide con l'origine O, la (35), essendo x0 = y0 = 0, si trasforma in:
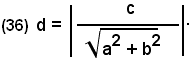
Si può affermare che:
-la distanza dell'origine dalla retta ax + by + c = 0 è data in valore assoluto dal rapporto fra il termine noto e la radice quadrata dei quadrati dei coefficienti di x e y della stessa equazione della retta.
Esempi
1)-Calcolare la distanza del punto P(2, 4) dalla retta di equazione x + 2y - 4 = 0.
Si applica la (35); il valore della distanza in questione si ottiene dopo aver sostituito alla x l'ascissa 2 di P e alla y l'ordinata 3, per la radice quadrata della somma dei quadrati dei coefficienti della x e della y dell'equazione, cioè:
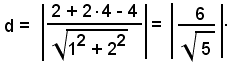
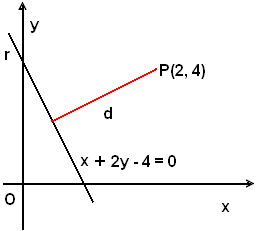
In base alla convenzione suddetta, la distanza di P(2, 4) da r, non orientata, è positiva in quanto le coordinate di P rendono positivo il primo membro dell'equazione della retta r.
Se non si ricorda la formula (35), si procede nel modo visto in precedenza, cioè: per il punto P si determina la perpendicolare alla retta, si trovano le coordinate del punto M d'intersezione delle due rette; la distanza PM, in valore assoluto, fornisce il valore della distanza di P da r. Nel caso specifico la retta perpendicolare alla r per P ha equazione:
2(x - 2) - (y - 4) = = 0,
cioè
2y - x = 0.
Le coordinate del punto M sono date dalla soluzione del sistema:
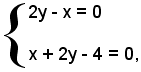
cioè
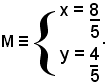
La distanza, in valore assoluto, di P da r viene data dalla distanza dei punti P e M:
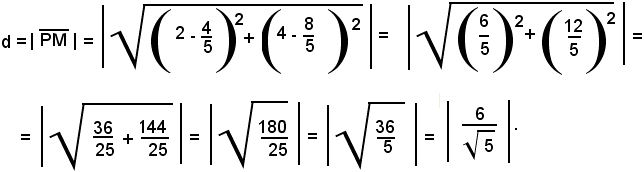
2)-Calcolare la distanza dell'origine dalla retta di equazione x + 2y - 4 = 0.
Applicando la (36), si ottiene:
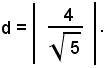
Se si osserva che O appartiene al semipiano opposto a quello in cui si trova il punto P, d dev'essere considerata negativa e quindi il suo valore è:
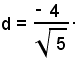
3)-Determinare la distanza fra le rette parallele di equazioni:
a) 4x - 5y = 4, b) 8x - 10y = 1.
Si consideri un punto P della retta b; la distanza di P dalla retta a è la distanza richiesta. Per determinare le coordinate di un punto della retta b, si deve trovare una soluzione dell'equazione 8x - 10y = 1. Allo scopo, si dà alla x il valore 2, che sostituito alla x nell'equazione di b, fornisce per la y il valore +3/2. P ha quindi coordinate (2, 3/2).
La distanza di P dalla retta a di equazione 4x - 5y = 4 è data da:
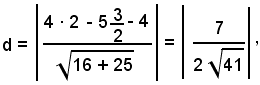
oppure si determina la distanza di un punto M qualsiasi della retta a dalla retta b.
Per x =1, si ha y = 0. Il punto M della retta a ha quindi coordinate 1 e 0. La distanza di M dalla retta, fornisce la distanza fra le rette parallele date; essa è data da:
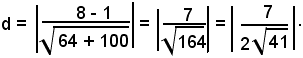
Si poteva seguire anche il seguente terzo procedimento: la distanza fra due rette parallele è data dalla differenza delle distanze dell'origine di esse.
La distanza dell'origine dalla retta a, per la (36), è data da:
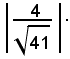
La distanza dell'origine dalla retta b, è data da:
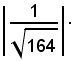
La distanza richiesta è:
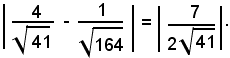
E' bene ricordare che:
Quando s'impone che il denominatore della (33) o della (34) sia uguale a zero, si ha una frazione con il denominatore nullo, che è priva di significato ma in geometria analitica si usa chiamare infinita una frazione con denominatore nullo e numeratore diverso da zero, indeterminata se numeratore e denominatore sono nulli. Si suole anche affermare "condizione necessaria perchè una frazione sia infinite è che il suo numeratore sia uguale a zero."
Esempi
1)-Trovare la tangente, il seno e il coseno dell'angolo ω formato dalle seguenti rette:
Essendo:
applicando la (34), si ha
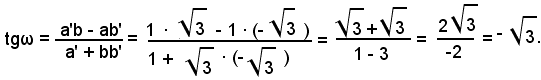
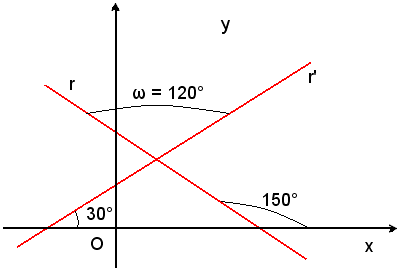
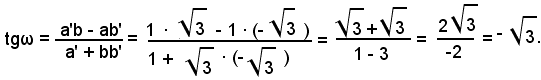
Essendo negativa la tangente dell'angolo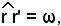 
tale angolo descritto da r' per sovrapporsi ad r dev'essere ottuso e quindi ω = 120°.
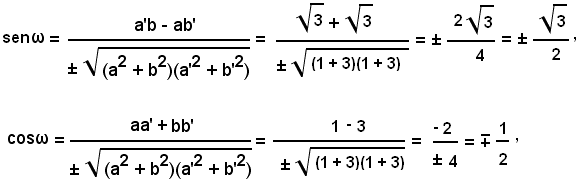
tale angolo descritto da r' per sovrapporsi ad r dev'essere ottuso e quindi ω = 120°.poichè è stato determinato
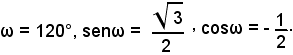
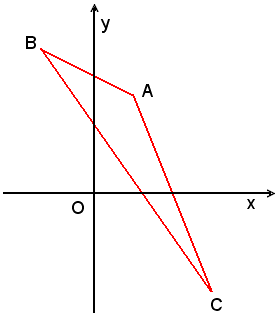
2)-Calcolare gli angoli del triangolo di vertici A(1, 2), B(-2, -3) C(3, -3).
Ricordando che il coefficiente angolare di una retta individuata mediante due punti P1(x1, y1) e P2(x2, y2) è dato dalla relazione (23), cioè da:
applicando la formula in tale caso, si trovano i coefficienti angolari m1, m2 , m3, rispettivamente delle rette AB, BC, CA:
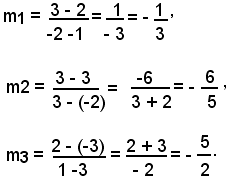
Da tali formule risulta:
Quindi, essendo noti i valori delle tangenti degli angoli, in corrispondenza di essi, si rileva dalle tavole il valore dei rispettivi angoli; essi sono:
Distanza di un punto da una retta
Data la retta r di equazione ax + by + c = 0 e un punto P(x0, y0) del piano, si definisce distanza del punto P dalla retta r la misura in valore assoluto del segmento di perpendicolare condotta dal punto alla retta data.
L'equazione della perpendicolare alla retta r per P, come è noto, è data da:
Le coordinate di M, punto d'intersezione della retta r con la retta perpendicolare, sono fornite dalla soluzione del sistema:
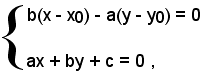
cioè
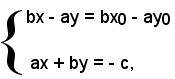
ossia
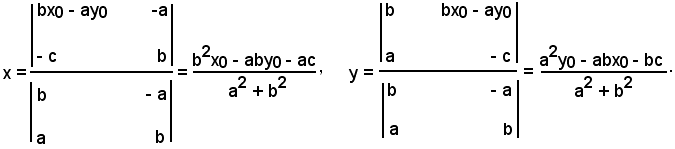
La distanza dei due punti P e M, fornisce la distanza di P dalla retta.
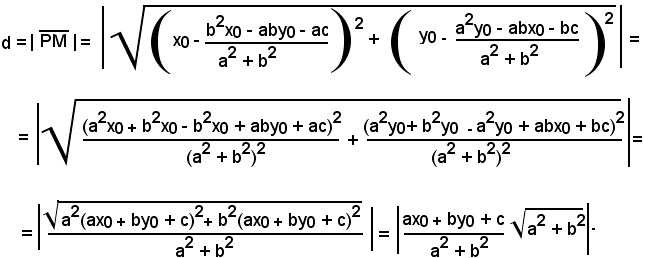
Quindi:
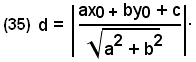
Si può affermare che:
-la distanza di un punto P(x0, y0) dalla retta ax + by + c = 0 è data in valore assoluto dal rapporto fra il valore che assume il primo membro dell'equazione della retta quando alle variabili x ed y si sostituiscono rispettivamente le coordinate x0 e y0 del punto e la radice quadrata della somma dei quadrati dei coefficienti di x e y dell'equazione della stessa retta.
Il segno di d è determinato quando è fissato il verso positivo di r.
Si osserva che la retta r divide il piano in due semipiani, punti appartenenti ad uno stesso semipiano hanno da r distanze dello stesso segno, precisamente, per una retta orientata, d è positiva per i punto che si trovano a sinistra di r rispetto ad un osservatore che percorre la retta nel senso positivo e d è negativo per quelli situati a destra.
Per una retta non orientata, si osserva che i due semipiani che la retta determina, sono caratterizzati dal fatto che le coordinate dei punto di uno rendono positivo il polinomio ax + by + c, primo membro dell'equazione della retta, e i punti dell'altro lo rendono negativo.
E' chiaro che, per passare da un punto del primo ad un punto del secondo, bisogna attraversare la retta. Convenzionalmente si può dire che i punti del semipiano che rendono positivo il polinomio ax + by + c hanno distanza positiva da r, di equazione ax + by + c = 0, mentre quelli che lo rendono negativo hanno distanza negativa.
Se il punto P(x0, y0) coincide con l'origine O, la (35), essendo x0 = y0 = 0, si trasforma in:
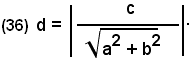
Si può affermare che:
-la distanza dell'origine dalla retta ax + by + c = 0 è data in valore assoluto dal rapporto fra il termine noto e la radice quadrata dei quadrati dei coefficienti di x e y della stessa equazione della retta.
Esempi
1)-Calcolare la distanza del punto P(2, 4) dalla retta di equazione x + 2y - 4 = 0.
Si applica la (35); il valore della distanza in questione si ottiene dopo aver sostituito alla x l'ascissa 2 di P e alla y l'ordinata 3, per la radice quadrata della somma dei quadrati dei coefficienti della x e della y dell'equazione, cioè:
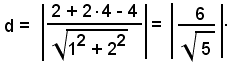
In base alla convenzione suddetta, la distanza di P(2, 4) da r, non orientata, è positiva in quanto le coordinate di P rendono positivo il primo membro dell'equazione della retta r.
Se non si ricorda la formula (35), si procede nel modo visto in precedenza, cioè: per il punto P si determina la perpendicolare alla retta, si trovano le coordinate del punto M d'intersezione delle due rette; la distanza PM, in valore assoluto, fornisce il valore della distanza di P da r. Nel caso specifico la retta perpendicolare alla r per P ha equazione:
2(x - 2) - (y - 4) = = 0,
cioè
Le coordinate del punto M sono date dalla soluzione del sistema:
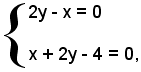
cioè
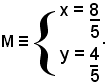
La distanza, in valore assoluto, di P da r viene data dalla distanza dei punti P e M:
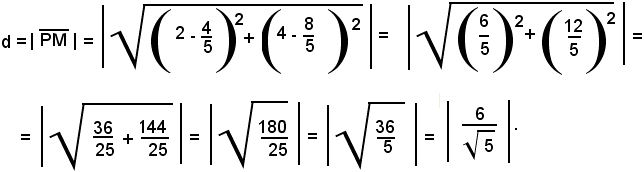
2)-Calcolare la distanza dell'origine dalla retta di equazione x + 2y - 4 = 0.
Applicando la (36), si ottiene:
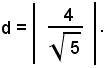
Se si osserva che O appartiene al semipiano opposto a quello in cui si trova il punto P, d dev'essere considerata negativa e quindi il suo valore è:
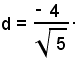
3)-Determinare la distanza fra le rette parallele di equazioni:
Si consideri un punto P della retta b; la distanza di P dalla retta a è la distanza richiesta. Per determinare le coordinate di un punto della retta b, si deve trovare una soluzione dell'equazione 8x - 10y = 1. Allo scopo, si dà alla x il valore 2, che sostituito alla x nell'equazione di b, fornisce per la y il valore +3/2. P ha quindi coordinate (2, 3/2).
La distanza di P dalla retta a di equazione 4x - 5y = 4 è data da:
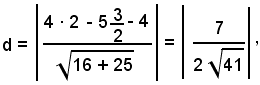
oppure si determina la distanza di un punto M qualsiasi della retta a dalla retta b.
Per x =1, si ha y = 0. Il punto M della retta a ha quindi coordinate 1 e 0. La distanza di M dalla retta, fornisce la distanza fra le rette parallele date; essa è data da:
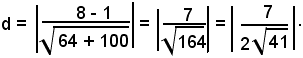
Si poteva seguire anche il seguente terzo procedimento: la distanza fra due rette parallele è data dalla differenza delle distanze dell'origine di esse.
La distanza dell'origine dalla retta a, per la (36), è data da:
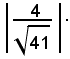
La distanza dell'origine dalla retta b, è data da:
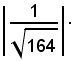
La distanza richiesta è: