MIKY & GENNY
FASCI DI RETTE E COMBINAZIONI LINEARI DI EQUAZIONI ---> INDICE
Fascio di rette
Si definisce fascio di rette la totalità delle rette passanti per un punto, detto centro del fascio, ossia le infinite rette passanti per un punto.
Determinazione dell'equazione del fascio di rette conoscendo le coordinate del centro P(x0, y0)
Sia ax + by + c = 0 l'equazione di una retta generica del piano e P(x0, y0) un punto.
Il punto P(x0, y0) appartiene alla retta, se e solo se le sue coordinate soddisfano la relazione:
(1) ax0 + by0 + c = 0.
La relazione (1) si chiama "condizione di appartenenza" del punto P(x0, y0) alla retta r.
Dalla (1) si ricava c = - ax0 - by0 e, sostituendo tale valore nell'equazione della retta, si ricava:
ax + by - ax0 - by0 = 0,
(2) a(x - x0) + b(y - y0) = 0,
per a = 0, si ha la retta del fascio parallela all'asse x di equazione y - y0 = 0;
per b = 0, si ha la retta del fascio parallela all'asse y di equazione x - x0 = 0.
Al variare dei coefficienti a e b la retta ruota attorno al punto P descrivendo il fascio di centro P. Non potendo essere a e b simultaneamente nulli, la (2) dipende da un solo coefficiente essenziale.
Determinazione dell'equazione del fascio date le equazioni delle due rette generatrici
Siano r e r' due rette rispettivamente di equazioni:
r) 2x - y - 5 = 0 e r') 3x - 4y - 15 = 0.
Si moltiplica ora la prima equazione per il fattore a, la seconda per il fattore b, ove a e b sono due numeri qualsiasi non contemporaneamente nulli e si sommano poi le due equazioni, ottenendo:
a(2x - y - 5) + b(3x - 4y - 15) = 0.
ossia
(3) (2a + 3b)x - (a + 3b)y - 5a -15b = 0.
La (3) si chiama combinazione lineare delle equazioni date.
Essa è un'equazione di primo grado nelle variabili x e y, perciò, rappresenta una retta nel piano cartesiano.
Le rette r e r' s'incontrano nel punto P di coordinate (1, -3), ottenute dalla risoluzione del sistema delle equazioni di r e r'.
Si osserva che anche la retta di equazione (3) passa per il punto P(1, -3).
Infatti, le coordinate (1, -3) di P soddisfano l'equazione (3):
a(2·1 + 3 - 5) + b(3+ 12 - 15) = a·0 + b·0 = 0.
Quindi la (3) rappresenta una retta che passa per il punto P comune alle due rette r e r'.
Si può quindi affermare che:
-una combinazione lineare delle equazioni di due rette passanti per un punto, rappresenta ancora una retta passante per quel punto.
Al variare di a e b la retta di equazione (3) ruota attorno al punto P descrivendo il fascio di rette di centro P. Poichè a e b non possono essere simultaneamente nulli, la (3) dipende dal rapporto:
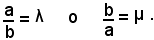
Al variare di λ, o μ, si ottengono le infinite rette passanti per il punto comune alle due rette date.
In tal modo, si ha una corrispondenza biunivoca e continua fra i valori di λ, o μ, e le rette del fascio, tale che ad ogni valore di λ, o μ, corrisponde una ed una sola retta del fascio e ad ogni retta del fascio corrisponde uno ed un solo valore di λ, o μ.
Per il valore particolare di a = 0, oppure λ = 0, si ottiene la retta r'; per il valore di b = 0, oppure λ = ∞, si ha la retta r.
Se r e r' sono parallele, l'equazione (3) fornisce il "fascio improprio di rette", cioè l'equazione di tutte le rette parallele alle rette date.
Si può quindi affermare che:
-una combinazione lineare delle equazioni di due rette è l'equazione del fascio individuato dalle due rette generatrici.
Il fascio è proprio se le rette generatrici sono incidenti, improprio se le rette sono parallele.
Tutte le rette di un fascio hanno per equazione la combinazione lineare di due rette generatrici.
Da ciò si deduce che:
-se tre rette passano per uno stesso punto, una qualunque delle tre equazioni è combinazione lineare delle altre due.
Esempio
Siano r e r' due rette rispettivamente di equazioni:
r) 3x + y - 1 = 0 e r') 4x - 2y + 5 = 0,
determinare:
1)-l'equazione del fascio da esse individuato;
2)-la retta del fascio parallela all'asse y;
3)-la retta del fascio perpendicolare alla retta di equazione 3x - 2y - 6 = 0;
4)-la retta del fascio che ha per coefficiente angolare m = 5;
5)-le rette del fascio che formano con i due assi cartesiani triangoli di area 1.
1)-L'equazione del fascio individuato dalle rette r e r' è la combinazione lineare delle equazioni delle due rette r e r', ossia:
(f) a(3x + y - 1) + b(4x - 2y + 5) = 0,
ossia
(f ') (3a + 4b)x + (a - 2b)y - a + 5b = 0.
2)-Una retta è parallela all'asse x quando la sua equazione manca del termine in x, cioè quando è nullo il coefficiente della x. Quindi, per avere l'equazione retta del fascio parallela all'asse x basta uguagliare a zero il coefficiente della x nella (f):
3a + 4b = 0,
cioè
3a = -4b,
ossia
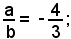
posto b = 1, si ha
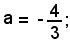
Sostituendo tali valori nella (f '), si ha:

ossia
10y - 19 = 0,
cioè
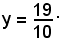
3)-La retta del fascio è perpendicolare alla retta di equazione 3x - 2y - 6 = 0 quando è soddisfatta la condizione di perpendicolarità tra due rette, cioè aa' - bb' = 0, come si è visto.
Nel caso specifico si ha:
3(3a + 4b) - 2(a - 2b) = 0,
da cui
9a + 12b - 2a + 4b = 0,
ossia
7a + 16b = 0.
Posto b = 1, si ricava:
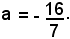
Sostituendo tali valori nella (f '), si ha:
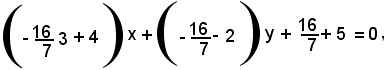
cioè
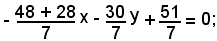
20x + 30y - 51 = 0.
4)-Il codfficiente angolare della retta (f ') è dato da:
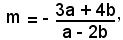
Uguagliando a 5 tale valore, per a e b si trova la condizione:
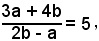
da cui, per b =1, si ha
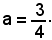
Sostituendo tali valori nella (f '), si ha:
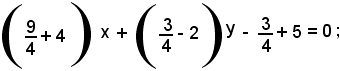
25x - 5y + 17 = 0.
5)-Una retta generica del fascio forma con gli assi x ed y un triangolo rettangolo MON, che ha per cateti OM e ON; poichè l'area del triangolo rettangolo è data dal semiprodotto dei cateti e, nel caso specifico essa è espressa da:

E' bene osservare che le misure dei segmenti che una retta stacca sugli assi possono essere tanto positivi quanto negativi, perciò per avere l'area del triangolo basta moltiplicare i loro valori assoluti.
Nel caso specifico, risulta:
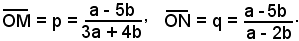
Quindi il semiprodotto delle misure dei segmenti è data da:
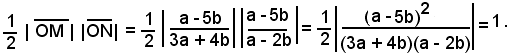
E' bene ricordare che:
-le intercette sugli assi della retta di equazione ax + by + c = 0 sono p = -c/a e q = - c/b.
-il prodotto dei valori assoluti è uguale al valore assoluto del prodotto, cioè |a| · |b| = |a · b|.
-se il valore assoluto di un numero è uguale a 1, il numero dev'essere uguale a +1 oppure a -1.
Quindi la relazione suddetta si sdoppia in:
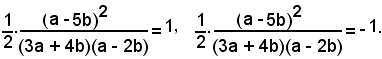
Sviluppando e ordinando si ottiene:
5a2 + 6ab - 41b2 = 0 e 7a2 - 14ab + 9b2 = 0
e posto b = 1, si ha:
5a2 + 6a - 41 = 0 e 7a2 - 14a + 9 = 0.
Per la prima equazione si ricavano i valori:

Sostituendo tali valori nella (f '), si ottengono le equazioni delle due rette che risolvono il problema, cioè le rette del fascio che formano con i due assi cartesiani triangoli di area 1;
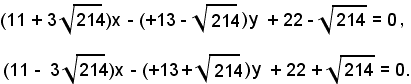
La seconda equazione fornisce valori immaginari di a, essendo:
Δ = 49 - 63 < 0.
Problema 1
Dati i punti A(4, 5), B(0, 4), C(-6, 0), trovare le equazioni delle tre mediane del triangolo ABC, dimostrare che esse appartengono allo stesso fascio, trovare infine le coordinate del centro del fascio.
Siano M, N, P i punti medi rispettivamente dei lati AB, BC, CA.
Le coordinate di tali punti sono rispettivamente:
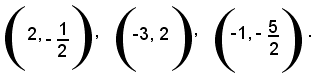
Le tre mediane sono le rette AN, CM, BP. Applicando la formula (9), già vista, relativa alle equazioni della retta, cioè:
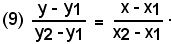
dopo facili calcoli, si ha:
AN) x + y + 1 = 0,
CM) x + 16y + 6 = 0,
BP) 13x - 2y + 8 = 0.
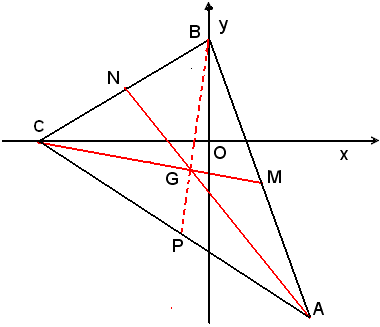
Per dimostrare che tre mediane del triangolo ABC passano per uno stesso punto, cioè appartengono ad uno stesso fascio, è sufficiente rilevare che una delle tre mediane passa per il punto comune alle altre due, cioè che l'equazione corrispondente di questa è combinazione lineare delle equazioni delle altre due rette.
Nota bene
La condizione geometrica che le tre mediane passino per uno stesso punto si trasforma nella condizione analitica che le tre equazioni nelle due variabili x e y ammettano una soluzione comune. In tal caso, una delle tre equazioni è combinazione lineare delle altre due.
Infatti, si osservi che l'equazione della mediana AN si ottiene sommando le due equazioni delle mediane CM e BP, cioè:
(13x - 2y + 8) + x + 16y + 6 = 0;
14x + 14y + 14 = 0;
x + y + 1 = 0.
Per trovare le coordinate del centro G del fascio, cioè il punto comune delle tre mediane, baricentro del triangolo, basta risolvere il sistema formato da due qualsiasi delle equazioni trovate:
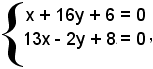
da cui
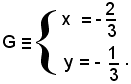
Verifica
Si ricorda che il baricentro G(x0, y0) di tre punti A(x1, y1), B(x2, y2), C(x3, y3) ha coordinate:

pertanto, nel caso specifico, risulta:
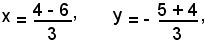
ossia

Problema 2
Trovare il centro del cerchio inscritto, incentro, del triangolo che ha per lati:
a) 3x - 4y + 3 = 0,
b) 3x + 4y + 6 = 0,
c) 15x + 8y - 30 = 0.
Il centro del cerchio inscritto nel triangolo, chiamato incentro, è dato dall'intersezione delle bisettrici degli angoli, interni, del triangolo.
Siano A, B, C i vertici del triangolo. Dalla geometria elementare è noto che la bisettrice di un angolo è il luogo geometrico dei punti del piano distanti dai lati del triangolo. Quindi si determinano le bisettrici degli angoli di vertici A, B e C, ricorrendo a tale proprietà.
Allo scopo, per determinare l'equazione della bisettrice dell'angolo di vertice A, sia P di coordinate x e y un punto generico di tale bisettrice.
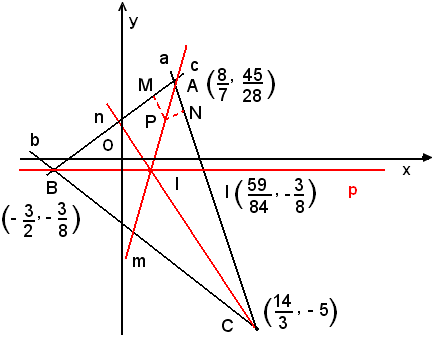
Affinchè P appartenga alla bisettrice dell'angolo di vertice A, occorre che la sua distanza dalla retta a sia uguale alla sua distanza dalla retta c, ossia: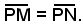
La distanza di P(x, y) dalla retta a è data da:
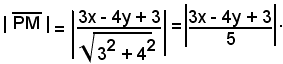
La distanza di P(x, y) dalla retta c è data da:
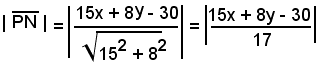
e, poichè
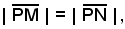
si ha:
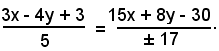
Tali equazioni fornisconi le bisettrici dell'angolo e dell'angolo supplementare.
e dell'angolo supplementare.
Scegliendo nell'equazione il segno del radicale in modo che nei due membri i termini noti, supposti non nulli, risultino dello stesso segno, si ottiene la bisettrice dell'angolo , angolo nel quale è posta l'origine. Se ai termini noti si assegnano invece segni opposti, si ha la bisettrice dell'angolo supplementare.
, angolo nel quale è posta l'origine. Se ai termini noti si assegnano invece segni opposti, si ha la bisettrice dell'angolo supplementare.
Infatti, nel primo caso, ogni punto (x, y) della bisettrice è situato dalla stessa banda dell'origine o da bande opposte sia rispetto alla a che rispetto alla c; nel secondo caso invece il punto (x, y) si trova, rispetto a una retta, dalla stessa banda dell'origine, rispetto all'altra retta da bande opposte.
L'equazione della bisettrice dell'angolo è:
è:
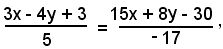
ossia
m) 126x - 28y - 99 = 0,
Procedendo nello stesso modo, si troveranno le equazioni delle altre due bisettrici:
n) 21x + 18y - 8 = 0,
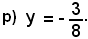
Risolvendo il sistema formato da due delle tre equazioni delle bisettrici, ad esempio la n) e la p), si determinano le coordinate di I, incentro. Esse sono:
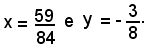 Si
verifica come tali valori soddisfino la prima equazione m), il che vuol
dire che la retta m) appartiene al fascio delle rette individuato da n)
e p), ossia la retta m) passa per il punto comune alle rette n e p.
Si
verifica come tali valori soddisfino la prima equazione m), il che vuol
dire che la retta m) appartiene al fascio delle rette individuato da n)
e p), ossia la retta m) passa per il punto comune alle rette n e p.
Determinazione dell'equazione del fascio di rette conoscendo le coordinate del centro P(x0, y0)
Sia ax + by + c = 0 l'equazione di una retta generica del piano e P(x0, y0) un punto.
Il punto P(x0, y0) appartiene alla retta, se e solo se le sue coordinate soddisfano la relazione:
La relazione (1) si chiama "condizione di appartenenza" del punto P(x0, y0) alla retta r.
Dalla (1) si ricava c = - ax0 - by0 e, sostituendo tale valore nell'equazione della retta, si ricava:
per a = 0, si ha la retta del fascio parallela all'asse x di equazione y - y0 = 0;
per b = 0, si ha la retta del fascio parallela all'asse y di equazione x - x0 = 0.
Al variare dei coefficienti a e b la retta ruota attorno al punto P descrivendo il fascio di centro P. Non potendo essere a e b simultaneamente nulli, la (2) dipende da un solo coefficiente essenziale.
Determinazione dell'equazione del fascio date le equazioni delle due rette generatrici
Siano r e r' due rette rispettivamente di equazioni:
r) 2x - y - 5 = 0 e r') 3x - 4y - 15 = 0.
Si moltiplica ora la prima equazione per il fattore a, la seconda per il fattore b, ove a e b sono due numeri qualsiasi non contemporaneamente nulli e si sommano poi le due equazioni, ottenendo:
a(2x - y - 5) + b(3x - 4y - 15) = 0.
ossia
(3) (2a + 3b)x - (a + 3b)y - 5a -15b = 0.
La (3) si chiama combinazione lineare delle equazioni date.
Essa è un'equazione di primo grado nelle variabili x e y, perciò, rappresenta una retta nel piano cartesiano.
Le rette r e r' s'incontrano nel punto P di coordinate (1, -3), ottenute dalla risoluzione del sistema delle equazioni di r e r'.
Si osserva che anche la retta di equazione (3) passa per il punto P(1, -3).
Infatti, le coordinate (1, -3) di P soddisfano l'equazione (3):
a(2·1 + 3 - 5) + b(3+ 12 - 15) = a·0 + b·0 = 0.
Quindi la (3) rappresenta una retta che passa per il punto P comune alle due rette r e r'.
Si può quindi affermare che:
-una combinazione lineare delle equazioni di due rette passanti per un punto, rappresenta ancora una retta passante per quel punto.
Al variare di a e b la retta di equazione (3) ruota attorno al punto P descrivendo il fascio di rette di centro P. Poichè a e b non possono essere simultaneamente nulli, la (3) dipende dal rapporto:
Al variare di λ, o μ, si ottengono le infinite rette passanti per il punto comune alle due rette date.
In tal modo, si ha una corrispondenza biunivoca e continua fra i valori di λ, o μ, e le rette del fascio, tale che ad ogni valore di λ, o μ, corrisponde una ed una sola retta del fascio e ad ogni retta del fascio corrisponde uno ed un solo valore di λ, o μ.
Per il valore particolare di a = 0, oppure λ = 0, si ottiene la retta r'; per il valore di b = 0, oppure λ = ∞, si ha la retta r.
Se r e r' sono parallele, l'equazione (3) fornisce il "fascio improprio di rette", cioè l'equazione di tutte le rette parallele alle rette date.
Si può quindi affermare che:
-una combinazione lineare delle equazioni di due rette è l'equazione del fascio individuato dalle due rette generatrici.
Il fascio è proprio se le rette generatrici sono incidenti, improprio se le rette sono parallele.
Tutte le rette di un fascio hanno per equazione la combinazione lineare di due rette generatrici.
Da ciò si deduce che:
-se tre rette passano per uno stesso punto, una qualunque delle tre equazioni è combinazione lineare delle altre due.
Esempio
Siano r e r' due rette rispettivamente di equazioni:
r) 3x + y - 1 = 0 e r') 4x - 2y + 5 = 0,
determinare:
1)-l'equazione del fascio da esse individuato;
2)-la retta del fascio parallela all'asse y;
3)-la retta del fascio perpendicolare alla retta di equazione 3x - 2y - 6 = 0;
4)-la retta del fascio che ha per coefficiente angolare m = 5;
5)-le rette del fascio che formano con i due assi cartesiani triangoli di area 1.
1)-L'equazione del fascio individuato dalle rette r e r' è la combinazione lineare delle equazioni delle due rette r e r', ossia:
ossia
2)-Una retta è parallela all'asse x quando la sua equazione manca del termine in x, cioè quando è nullo il coefficiente della x. Quindi, per avere l'equazione retta del fascio parallela all'asse x basta uguagliare a zero il coefficiente della x nella (f):
cioè
3a = -4b,
ossia
posto b = 1, si ha
Sostituendo tali valori nella (f '), si ha:

ossia
10y - 19 = 0,
cioè
3)-La retta del fascio è perpendicolare alla retta di equazione 3x - 2y - 6 = 0 quando è soddisfatta la condizione di perpendicolarità tra due rette, cioè aa' - bb' = 0, come si è visto.
Nel caso specifico si ha:
da cui
9a + 12b - 2a + 4b = 0,
ossia
7a + 16b = 0.
Posto b = 1, si ricava:
Sostituendo tali valori nella (f '), si ha:
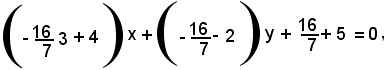
cioè
20x + 30y - 51 = 0.
4)-Il codfficiente angolare della retta (f ') è dato da:
Uguagliando a 5 tale valore, per a e b si trova la condizione:
da cui, per b =1, si ha
Sostituendo tali valori nella (f '), si ha:
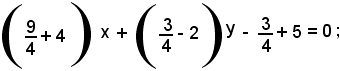
25x - 5y + 17 = 0.
5)-Una retta generica del fascio forma con gli assi x ed y un triangolo rettangolo MON, che ha per cateti OM e ON; poichè l'area del triangolo rettangolo è data dal semiprodotto dei cateti e, nel caso specifico essa è espressa da:

E' bene osservare che le misure dei segmenti che una retta stacca sugli assi possono essere tanto positivi quanto negativi, perciò per avere l'area del triangolo basta moltiplicare i loro valori assoluti.
Nel caso specifico, risulta:
Quindi il semiprodotto delle misure dei segmenti è data da:
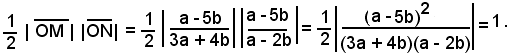
E' bene ricordare che:
-le intercette sugli assi della retta di equazione ax + by + c = 0 sono p = -c/a e q = - c/b.
-il prodotto dei valori assoluti è uguale al valore assoluto del prodotto, cioè |a| · |b| = |a · b|.
-se il valore assoluto di un numero è uguale a 1, il numero dev'essere uguale a +1 oppure a -1.
Quindi la relazione suddetta si sdoppia in:
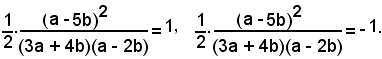
Sviluppando e ordinando si ottiene:
5a2 + 6ab - 41b2 = 0 e 7a2 - 14ab + 9b2 = 0
e posto b = 1, si ha:
5a2 + 6a - 41 = 0 e 7a2 - 14a + 9 = 0.
Per la prima equazione si ricavano i valori:

Sostituendo tali valori nella (f '), si ottengono le equazioni delle due rette che risolvono il problema, cioè le rette del fascio che formano con i due assi cartesiani triangoli di area 1;
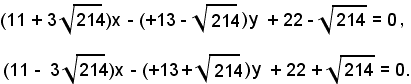
La seconda equazione fornisce valori immaginari di a, essendo:
Problema 1
Dati i punti A(4, 5), B(0, 4), C(-6, 0), trovare le equazioni delle tre mediane del triangolo ABC, dimostrare che esse appartengono allo stesso fascio, trovare infine le coordinate del centro del fascio.
Siano M, N, P i punti medi rispettivamente dei lati AB, BC, CA.
Le coordinate di tali punti sono rispettivamente:

Le tre mediane sono le rette AN, CM, BP. Applicando la formula (9), già vista, relativa alle equazioni della retta, cioè:
dopo facili calcoli, si ha:
AN) x + y + 1 = 0,
CM) x + 16y + 6 = 0,
BP) 13x - 2y + 8 = 0.

Per dimostrare che tre mediane del triangolo ABC passano per uno stesso punto, cioè appartengono ad uno stesso fascio, è sufficiente rilevare che una delle tre mediane passa per il punto comune alle altre due, cioè che l'equazione corrispondente di questa è combinazione lineare delle equazioni delle altre due rette.
Nota bene
La condizione geometrica che le tre mediane passino per uno stesso punto si trasforma nella condizione analitica che le tre equazioni nelle due variabili x e y ammettano una soluzione comune. In tal caso, una delle tre equazioni è combinazione lineare delle altre due.
Infatti, si osservi che l'equazione della mediana AN si ottiene sommando le due equazioni delle mediane CM e BP, cioè:
(13x - 2y + 8) + x + 16y + 6 = 0;
14x + 14y + 14 = 0;
x + y + 1 = 0.
Per trovare le coordinate del centro G del fascio, cioè il punto comune delle tre mediane, baricentro del triangolo, basta risolvere il sistema formato da due qualsiasi delle equazioni trovate:
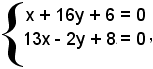
da cui
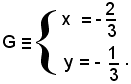
Verifica
Si ricorda che il baricentro G(x0, y0) di tre punti A(x1, y1), B(x2, y2), C(x3, y3) ha coordinate:
pertanto, nel caso specifico, risulta:
ossia
Problema 2
Trovare il centro del cerchio inscritto, incentro, del triangolo che ha per lati:
a) 3x - 4y + 3 = 0,
b) 3x + 4y + 6 = 0,
c) 15x + 8y - 30 = 0.
Il centro del cerchio inscritto nel triangolo, chiamato incentro, è dato dall'intersezione delle bisettrici degli angoli, interni, del triangolo.
Siano A, B, C i vertici del triangolo. Dalla geometria elementare è noto che la bisettrice di un angolo è il luogo geometrico dei punti del piano distanti dai lati del triangolo. Quindi si determinano le bisettrici degli angoli di vertici A, B e C, ricorrendo a tale proprietà.
Allo scopo, per determinare l'equazione della bisettrice dell'angolo di vertice A, sia P di coordinate x e y un punto generico di tale bisettrice.

Affinchè P appartenga alla bisettrice dell'angolo di vertice A, occorre che la sua distanza dalla retta a sia uguale alla sua distanza dalla retta c, ossia:
La distanza di P(x, y) dalla retta a è data da:
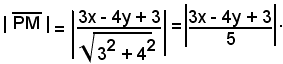
La distanza di P(x, y) dalla retta c è data da:
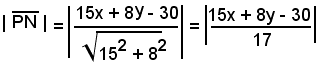
e, poichè
si ha:
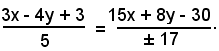
Tali equazioni fornisconi le bisettrici dell'angolo
Scegliendo nell'equazione il segno del radicale in modo che nei due membri i termini noti, supposti non nulli, risultino dello stesso segno, si ottiene la bisettrice dell'angolo
Infatti, nel primo caso, ogni punto (x, y) della bisettrice è situato dalla stessa banda dell'origine o da bande opposte sia rispetto alla a che rispetto alla c; nel secondo caso invece il punto (x, y) si trova, rispetto a una retta, dalla stessa banda dell'origine, rispetto all'altra retta da bande opposte.
L'equazione della bisettrice dell'angolo
ossia
m) 126x - 28y - 99 = 0,
Procedendo nello stesso modo, si troveranno le equazioni delle altre due bisettrici:
n) 21x + 18y - 8 = 0,
Risolvendo il sistema formato da due delle tre equazioni delle bisettrici, ad esempio la n) e la p), si determinano le coordinate di I, incentro. Esse sono: