MIKY & GENNY
IPERBOLE E COMPLEMENTI ---> INDICE
Definizione
- Si chiama iperbole il luogo geometrico dei punti del piano per cui la
differenza delle distanze da due punti dati è costante.
I punti dati si chiamano fuochi dell'iperbole e si indicano con F e F'; si indica inoltre con 2c la lunghezza del segmento F'F e con 2a il valore assoluto della differenza costante delle distanze di un punto generico P dell'iperbole dai fuochi F e F'.
Dalla definizione di iperbole si ha:
(1) |PF' - PF| = 2a.
L'iperbole è formata da due rami:
-se PF' > PF, si ha il ramo di destra;
-se PF' < PF, si ha il ramo di sinistra.
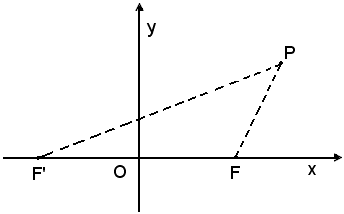
Poichè nel triangolo F'PF un lato è maggiore della differenza degli altri due, si ha:
cioè,
2c > 2a,
ossia,
c > a.
Per determinare l'equazione cartesiana dell'iperbole si assume come asse x la retta F'F e come asse y la perpendicolare nel punto medio O del segmento F'F. Poichè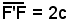
,
le coordinate dei fuochi sono F(c, 0) e F'(-c, 0). Indicando con x e y
le coordinate del generico punto P dell'iperbole, la (1) si traduce
analiticamente come segue:
-se PF' - PF = 2a, risulta
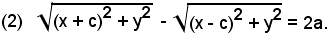
-se PF' - PF = - 2a, la (2) si traduce in
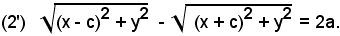
Nella (2), si porta il secondo radicale al secondo membro e si eleva al quadrato e, sviluppando e semplificando, si ha:
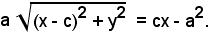
Elevando ancora al quadrato e semplificando, risulta:
(a2 - c2)x2 + a2y2 = a2(a2 - c2).
Siccome a < c, risulta a2 - c2 < 0, cioè c2 - a2 > 0, si pone quindi:
(3) c2 - a2 = b2.
Sostituendo nell'espressione precedente, si ha:
-b2x2 + a2y2 = -a2b2,
cioè
b2x2 - a2y2 = a2b2,
dividendo per a2b2, si ottiene l'equazione canonica dell'iperbole.
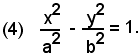
Proprietà dell'iperbole
a)-Proprietà di simmetria
Poichè nella (4) le variabili x ed y sono di grado pari, l'iperbole è simmetrica rispetto agli assi x, y e all'origine delle coordinate.
Gli assi x, y e l'origine O, si chiamano rispettivamente assi e centro di simmetria dell'iperbole.
b)-Vertici
L'asse x incontra l'iperbole in due punti reali A e A', le cui coordinate sono date dalle soluzioni del sistema seguente:
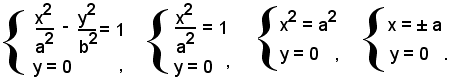
I due punti reali A,(a, 0), A'(-a, 0) si chiamano vertici dell'iperbole.
L'asse y non ha intersezioni reali con l'iperbole. Infatti, il sistema:
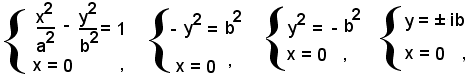
ammette soluzioni immaginarie; l'asse delle y si chiama asse non trasverso, il segmento di misura b semiasse ideale.
c)-Risolvendo l'equazione dell'iperbole rispetto alla variabile y, si ha:
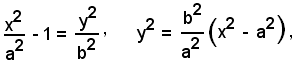
cioè
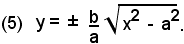
Affinchè la y abbia valori reali, occorre che:
x2 + a2 ≥ 0,
ossia
|x| ≥ a,
cioè
x ≥ a,
oppure
x ≤ - a.
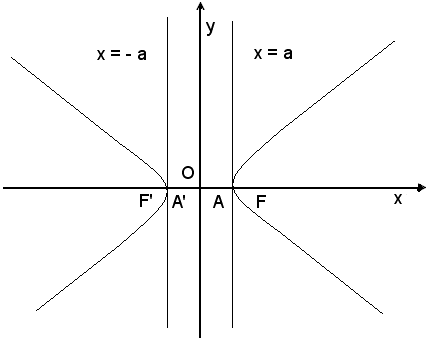
Si hanno allora i punti reali della curva solo all'esterno della striscia limitata dalle rette x = a ed x = - a.
La curva si compone di due parti staccate dette rami.
Le rette x = a e x = - a sono rispettivamente le tangenti all'iperbole nei punti A e A'.
Dalla (5) si osserva che, quando la x cresce, cresce anche la y; se x tende all'∞ anche la y tende all'∞; i due rami si estendono dunque, entrambi all'∞.
c')-Risolvendo l'equazione dell'iperbole rispetto alla variabile x, si ha:
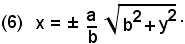
essendo b2 + y2 sempre positivo, la (6) non determina alcuna limitazione per la y, quindi ogni retta parallela all'asse x incontra la curva in due punti reali.
Asintoti
Le intersezioni dell'iperbole con una retta generica uscente dall'origine sono date dalle soluzioni del sistema:
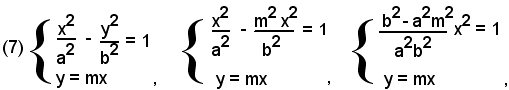
cioè
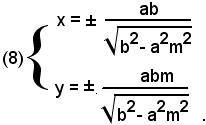
Tali intersezioni sono reali se b2 - a2m2 ≥ 0, cioè ricordando che un radicale quadratico ha valori reali se e solo se il radicando è positivo o nullo.
Se b2 - a2m2 = 0, cioè se
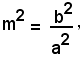
ossia se
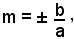
il denominatore della x e della y si annulla, cioè i valori di x ed y aumentano di valore ogni oltre limite, ossia le due intersezioni dell'iperbole con una retta uscente dall'origine e avente coefficiente angolare
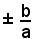
cadono entrambe all'infinito. Dunque, le rette di equazioni
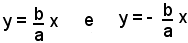
sono tangenti all'iperbole nei punti all'infinito; cioè le rette
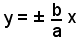
incontrano l'iperbole in due punti coincidenti ove la retta è tangente alla curva; si dice allora che le rette
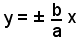
sono tangenti all'iperbole all'infinito.
Tali rette si chiamano asintoti dell'iperbole.
L'equazione complessiva degli asintoti è data da:
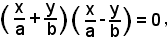
cioè
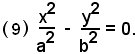
Essa si ottiene uguagliando a zero il primo membro della (4). In conclusione:
-l'iperbole ammette due punti all'infinito; le tangenti nei punti all'infinito passano per il centro dell'iperbole e si chiamano asintoti.
Poichè gli asintoti di un'iperbole hanno coefficienti angolari opposti, cioè
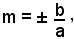
essi formano con l'asse x angoli supplementari. Quindi:
-gli assi di un'iperbole bisecano gli angoli formati dagli asintoti.
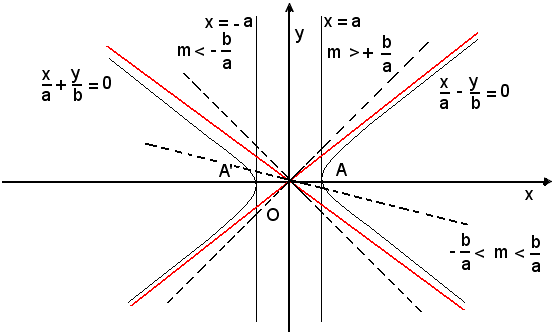
Si considerano ora i casi:
1) b2 - a2m2> 0,
cioè
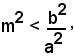
ossia
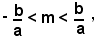
la retta uscente da O è contenuta per intero nell'angolo completo, formato dagli asintoti, in cui cade l'asse trasverso, l'asse x. In tal caso il sistema (7) ammette due soluzioni reali, cioè la retta uscente da O incontra l'iperbole in due punti simmetrici rispetto all'origine.
2) b2 - a2m2 < 0,
cioè
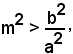
ossia
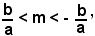
la retta uscente da O è contenuta nell'angolo formato dagli asintoti, in cui cade l'asse non trasverso, asse y. In tal caso il sistema (7) non ammette soluzioni reali, cioè la retta uscente da O non incontra l'iperbole.
L'iperbole è dunque tutta contenuta nell'angolo completo formato dagli asintoti, in cui cade l'asse trasverso.
Nota bene
Si chiama angolo completo la figura formata da un angolo e dal suo opposto al vertice.
Esempi
1)-Scrivere l'equazione del luogo geometrico dei punti del piano le cui distanze da F(5, 0) e F'(-5, 0) hanno differenza uguale, in valore assoluto, a 8.
Indicando con P un generico punto del piano di coordinate x ed y, la distanza di P da F è data da:
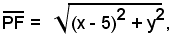
mentre la distanza di P da F' è
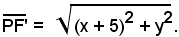
Il punto P(x, y) appartiene al luogo richiesto, se soddisfa la condizione
|PF' - PF| = 2a = 8.
Analiticamente tale relazione si traduce in
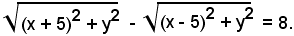
Passando il secondo radicale al secondo membro ed elevando al quadrato, si ha:
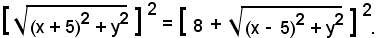
Sviluppando e riducendo, si ricava
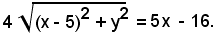
Elevando ancora al quadrato, si ha
16(x2 - 10x + 25 + y2) = 25x2 - 160x + 256,
ossia
9x2 - 16y2 = 144,
in definitiva
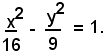
Il luogo richiesto rappresenta l'iperbole avente per centro l'origine O e per asse trasverso l'asse x.
2)-Determinare i semiassi, la distanza focale e gli asintoti dell'iperbole:
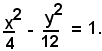
Il semiasse trasverso dell'iperbole ha valore:
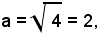
mentre quello non trasverso
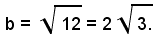
La distanza focale risulta
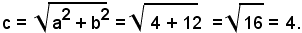
L'equazione complessiva degli asintoti si ottiene uguagliando a zero il primo membro dell'equazione dell'iperbole:
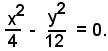
Tale equazione si può scrivere sotto la forma seguente:
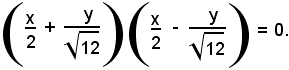
Gli asintoti hanno dunque equazione:
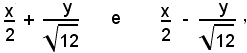
ossia
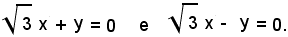
Poichè il coefficiente angolare dell'asintoto
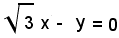
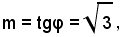
l'angolo completo in cui cade la curva è φ = 60°.
3)-Determinare i semiassi, la distanza focale e gli asintoti dell'iperbole
16x2 - 9y2 = 144.
Dividendo per 144, si ha l'equazione dell'iperbole sotto forma canonica:
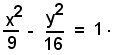
Procedendo come nell'esempio precedente, si ha:
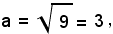
semiasse trasverso,
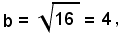
semiasse non trasverso; la distanza focale
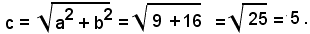
Gi asintoti hanno equazioni:
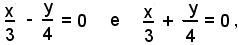
cioè
4x - 3y = 0 e 4x + 3y = 0.
L'angolo completo in cui cade l'iperbole è φ = 58° 8', essendo tgφ = 4/3.
Relazioni fra assi, fuochi e asintoti dell'iperbole
Dalle proprietà esaminate dell'iperbole, si rileva come gli asintoti risultano le rette diagonali del rettangolo di lati
Poichè la distanza focale 
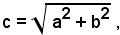l'ascissa c del fuoco è l'ipotenusa del triangolo rettangolo
avente per cateti i due semiassi a e b, da qui una semplice costruzione
dei fuochi dell'iperbole dati i semiassi a e b, come in figura.
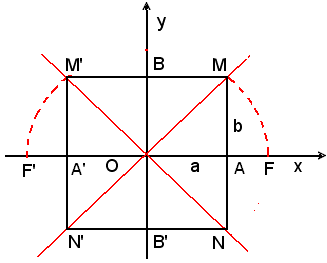
Le intersezioni del cerchio di centro O e raggio OM con l'asse trasverso danno i fuochi richiesti.
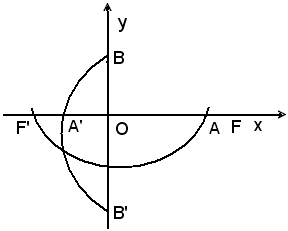
Viceversa, dati i fuochi e il semiasse trasverso a, gli estremi B e B' dell'asse non trasverso si ottengono come intersezioni del cerchio di centro O e raggio c con la perpendicolare all'asse trasverso condotta per il suo punto medio O, come in figura.
Così, noti i fuochi e gli estremi B e B' dell'asse non trasverso, si costruiscono gli estremi A e A' dell'asse trasverso come intersezioni del cerchio di centro B e raggio c con l'asse focale.
Iperbole equilatera - Equazione riferita agli asintoti
Un'iperbole si dice equilatera quando i suoi assi sono uguali.
L'equazione
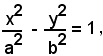
essendo a = b, diventa:
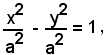
cioè
(10) x2 - y2 = a2.
L'equazione complessiva degli asintoti risulta quindi:
(11) x2 - y2 = a2,
che si decompone in
x + y = 0 e x - y = 0.
Quest'ultime due sono le equazioni delle bisettrici degli angoli formati dagli assi.
L'iperbole equilatera ha quindi per asintoti le bisettrici degli angoli formati dagli assi, pertanto si può affermare che:
-un'iperbole si dice equilatera quando ha gli asintoti perpendicolari fra loro.
I punti dati si chiamano fuochi dell'iperbole e si indicano con F e F'; si indica inoltre con 2c la lunghezza del segmento F'F e con 2a il valore assoluto della differenza costante delle distanze di un punto generico P dell'iperbole dai fuochi F e F'.
Dalla definizione di iperbole si ha:
(1) |PF' - PF| = 2a.
L'iperbole è formata da due rami:
-se PF' > PF, si ha il ramo di destra;
-se PF' < PF, si ha il ramo di sinistra.
Poichè nel triangolo F'PF un lato è maggiore della differenza degli altri due, si ha:
cioè,
2c > 2a,
ossia,
c > a.
Per determinare l'equazione cartesiana dell'iperbole si assume come asse x la retta F'F e come asse y la perpendicolare nel punto medio O del segmento F'F. Poichè
,
le coordinate dei fuochi sono F(c, 0) e F'(-c, 0). Indicando con x e y
le coordinate del generico punto P dell'iperbole, la (1) si traduce
analiticamente come segue:-se PF' - PF = 2a, risulta
-se PF' - PF = - 2a, la (2) si traduce in
Nella (2), si porta il secondo radicale al secondo membro e si eleva al quadrato e, sviluppando e semplificando, si ha:
Elevando ancora al quadrato e semplificando, risulta:
(a2 - c2)x2 + a2y2 = a2(a2 - c2).
Siccome a < c, risulta a2 - c2 < 0, cioè c2 - a2 > 0, si pone quindi:
(3) c2 - a2 = b2.
Sostituendo nell'espressione precedente, si ha:
-b2x2 + a2y2 = -a2b2,
cioè
b2x2 - a2y2 = a2b2,
dividendo per a2b2, si ottiene l'equazione canonica dell'iperbole.
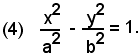
Proprietà dell'iperbole
a)-Proprietà di simmetria
Poichè nella (4) le variabili x ed y sono di grado pari, l'iperbole è simmetrica rispetto agli assi x, y e all'origine delle coordinate.
Gli assi x, y e l'origine O, si chiamano rispettivamente assi e centro di simmetria dell'iperbole.
b)-Vertici
L'asse x incontra l'iperbole in due punti reali A e A', le cui coordinate sono date dalle soluzioni del sistema seguente:
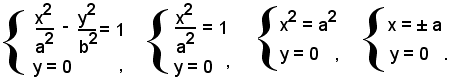
I due punti reali A,(a, 0), A'(-a, 0) si chiamano vertici dell'iperbole.
L'asse y non ha intersezioni reali con l'iperbole. Infatti, il sistema:
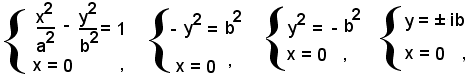
ammette soluzioni immaginarie; l'asse delle y si chiama asse non trasverso, il segmento di misura b semiasse ideale.
c)-Risolvendo l'equazione dell'iperbole rispetto alla variabile y, si ha:
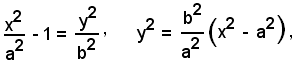
cioè
Affinchè la y abbia valori reali, occorre che:
x2 + a2 ≥ 0,
ossia
|x| ≥ a,
cioè
x ≥ a,
oppure
x ≤ - a.
Si hanno allora i punti reali della curva solo all'esterno della striscia limitata dalle rette x = a ed x = - a.
La curva si compone di due parti staccate dette rami.
Le rette x = a e x = - a sono rispettivamente le tangenti all'iperbole nei punti A e A'.
Dalla (5) si osserva che, quando la x cresce, cresce anche la y; se x tende all'∞ anche la y tende all'∞; i due rami si estendono dunque, entrambi all'∞.
c')-Risolvendo l'equazione dell'iperbole rispetto alla variabile x, si ha:
essendo b2 + y2 sempre positivo, la (6) non determina alcuna limitazione per la y, quindi ogni retta parallela all'asse x incontra la curva in due punti reali.
Asintoti
Le intersezioni dell'iperbole con una retta generica uscente dall'origine sono date dalle soluzioni del sistema:
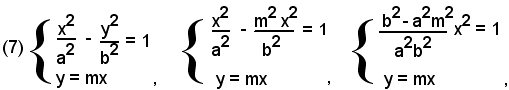
cioè
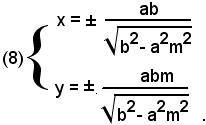
Tali intersezioni sono reali se b2 - a2m2 ≥ 0, cioè ricordando che un radicale quadratico ha valori reali se e solo se il radicando è positivo o nullo.
Se b2 - a2m2 = 0, cioè se
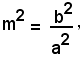
ossia se
il denominatore della x e della y si annulla, cioè i valori di x ed y aumentano di valore ogni oltre limite, ossia le due intersezioni dell'iperbole con una retta uscente dall'origine e avente coefficiente angolare
cadono entrambe all'infinito. Dunque, le rette di equazioni
sono tangenti all'iperbole nei punti all'infinito; cioè le rette
incontrano l'iperbole in due punti coincidenti ove la retta è tangente alla curva; si dice allora che le rette
sono tangenti all'iperbole all'infinito.
Tali rette si chiamano asintoti dell'iperbole.
L'equazione complessiva degli asintoti è data da:
cioè
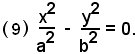
Essa si ottiene uguagliando a zero il primo membro della (4). In conclusione:
-l'iperbole ammette due punti all'infinito; le tangenti nei punti all'infinito passano per il centro dell'iperbole e si chiamano asintoti.
Poichè gli asintoti di un'iperbole hanno coefficienti angolari opposti, cioè
essi formano con l'asse x angoli supplementari. Quindi:
-gli assi di un'iperbole bisecano gli angoli formati dagli asintoti.
Si considerano ora i casi:
1) b2 - a2m2> 0,
cioè
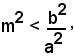
ossia
la retta uscente da O è contenuta per intero nell'angolo completo, formato dagli asintoti, in cui cade l'asse trasverso, l'asse x. In tal caso il sistema (7) ammette due soluzioni reali, cioè la retta uscente da O incontra l'iperbole in due punti simmetrici rispetto all'origine.
2) b2 - a2m2 < 0,
cioè
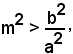
ossia
la retta uscente da O è contenuta nell'angolo formato dagli asintoti, in cui cade l'asse non trasverso, asse y. In tal caso il sistema (7) non ammette soluzioni reali, cioè la retta uscente da O non incontra l'iperbole.
L'iperbole è dunque tutta contenuta nell'angolo completo formato dagli asintoti, in cui cade l'asse trasverso.
Nota bene
Si chiama angolo completo la figura formata da un angolo e dal suo opposto al vertice.
Esempi
1)-Scrivere l'equazione del luogo geometrico dei punti del piano le cui distanze da F(5, 0) e F'(-5, 0) hanno differenza uguale, in valore assoluto, a 8.
Indicando con P un generico punto del piano di coordinate x ed y, la distanza di P da F è data da:
mentre la distanza di P da F' è
Il punto P(x, y) appartiene al luogo richiesto, se soddisfa la condizione
|PF' - PF| = 2a = 8.
Analiticamente tale relazione si traduce in
Passando il secondo radicale al secondo membro ed elevando al quadrato, si ha:
Sviluppando e riducendo, si ricava
Elevando ancora al quadrato, si ha
16(x2 - 10x + 25 + y2) = 25x2 - 160x + 256,
ossia
9x2 - 16y2 = 144,
in definitiva
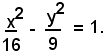
Il luogo richiesto rappresenta l'iperbole avente per centro l'origine O e per asse trasverso l'asse x.
2)-Determinare i semiassi, la distanza focale e gli asintoti dell'iperbole:
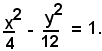
Il semiasse trasverso dell'iperbole ha valore:
mentre quello non trasverso
La distanza focale risulta
L'equazione complessiva degli asintoti si ottiene uguagliando a zero il primo membro dell'equazione dell'iperbole:
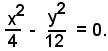
Tale equazione si può scrivere sotto la forma seguente:
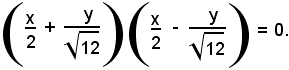
Gli asintoti hanno dunque equazione:
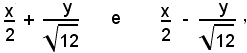
ossia
Poichè il coefficiente angolare dell'asintoto
è
l'angolo completo in cui cade la curva è φ = 60°.
3)-Determinare i semiassi, la distanza focale e gli asintoti dell'iperbole
16x2 - 9y2 = 144.
Dividendo per 144, si ha l'equazione dell'iperbole sotto forma canonica:
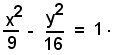
Procedendo come nell'esempio precedente, si ha:
semiasse trasverso,
semiasse non trasverso; la distanza focale
Gi asintoti hanno equazioni:
cioè
4x - 3y = 0 e 4x + 3y = 0.
L'angolo completo in cui cade l'iperbole è φ = 58° 8', essendo tgφ = 4/3.
Relazioni fra assi, fuochi e asintoti dell'iperbole
Dalle proprietà esaminate dell'iperbole, si rileva come gli asintoti risultano le rette diagonali del rettangolo di lati
Poichè la distanza focale l'ascissa c del fuoco è l'ipotenusa del triangolo rettangolo
avente per cateti i due semiassi a e b, da qui una semplice costruzione
dei fuochi dell'iperbole dati i semiassi a e b, come in figura.Le intersezioni del cerchio di centro O e raggio OM con l'asse trasverso danno i fuochi richiesti.
Viceversa, dati i fuochi e il semiasse trasverso a, gli estremi B e B' dell'asse non trasverso si ottengono come intersezioni del cerchio di centro O e raggio c con la perpendicolare all'asse trasverso condotta per il suo punto medio O, come in figura.
Così, noti i fuochi e gli estremi B e B' dell'asse non trasverso, si costruiscono gli estremi A e A' dell'asse trasverso come intersezioni del cerchio di centro B e raggio c con l'asse focale.
Iperbole equilatera - Equazione riferita agli asintoti
Un'iperbole si dice equilatera quando i suoi assi sono uguali.
L'equazione
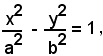
essendo a = b, diventa:
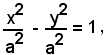
cioè
(10) x2 - y2 = a2.
L'equazione complessiva degli asintoti risulta quindi:
(11) x2 - y2 = a2,
che si decompone in
x + y = 0 e x - y = 0.
Quest'ultime due sono le equazioni delle bisettrici degli angoli formati dagli assi.
L'iperbole equilatera ha quindi per asintoti le bisettrici degli angoli formati dagli assi, pertanto si può affermare che:
-un'iperbole si dice equilatera quando ha gli asintoti perpendicolari fra loro.
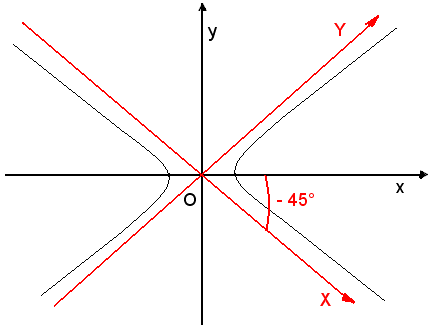
Si vede ora come si presenta l'equazione (10) quando si assumono come assi cartesiani gli
asintoti.
Si indicano con x e y le rette, asintoti, x + y = 0 e x - y = 0 e si fanno ruotare di un angolo di (- 45°) gli assi x ed y intorno all'origine 0. Sostituendo nella (10) ad x ed y rispettivamente:
x = Xcos(-45°) - Ysen(-45°),
y = Xsen(-45°) + Ycos(-45°),
e ciò ricordando le formule di rotazione degli assi e che
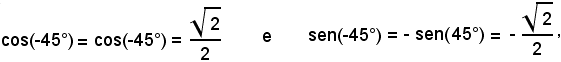
risulta
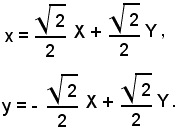
si ha
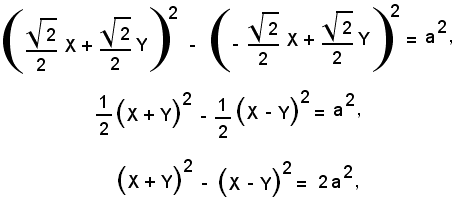
ossia
2XY + 2XY = 2a2,
4XY = 2a2,
cioè
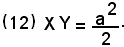
La (12) rappresenta l'equazione dell'iperbole equilatera riferita agli asintoti.
Viceversa, ogni equazione del tipo (13) xy = k rappresenta un'iperbole equilatera che ha gli assi cartesiani come asintoti.
In generale, l'equazione di un'iperbole riferita agli asintoti di equazioni
ax + by + c = 0 e a'x + b'y + c' = 0
Se k > 0, l'asse trasverso dell'iperbole (13) è la bisettrice del primo e del terzo quadrante ed ha per lunghezza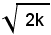
.
Se k < 0, l'asse trasverso dell'iperbole (13) è la bisettrice del secondo e del quarto quadrante ed ha per lunghezza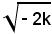
.
Un'iperbole equilatera avente come asintoti le rette
e quindi avente centro C (a, b), ha equazione del tipo:
(x - a)(y - b) = k,
sviluppando
xy - bx - ay + ab - k = 0
e posto
ab - k = c
risulta
Viceversa, qualunque equazione del tipo (1) rappresenta un'iperbole equilatera di centro C(a, b) ed avente per asintoti le rette x - a = 0 e y - b = 0.
L'equazione (14), risolta rispetto alla y diventa:
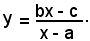
Si può quindi affermare che, qualsiasi equazione del tipo
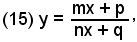
con mq≠np, rappresenta un'iperbole avente per centro
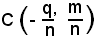
e per asintoti le rette
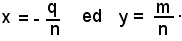
Nota bene
Se mq = np, l'equazione (15) rappresenta la retta
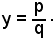
Infatti, da mq = np, si ha che
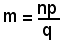e, sostituendo tale valore nella (15), si ricava:
Esempio
Scrivere l'equazione dell'iperbole equilatera avente per asintoti gli assi cartesiani e passante per il punto P(1, 2). L'equazione dell'iperbole è del tipo xy = k.
Affinchè la curva passi per P, le coordinate 1 e 2 devono soddisfare l'equazione, cioè dev'essere:
1 · 2 = k,
da cui
k = 2.
L'equazione dell'iperbole richiesta è
xy = 2.
I semiassi hanno lunghezza
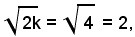
la distanza focale
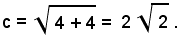
Intersezioni dell'iperbole con delle rette
Determinare le intersezioni dell'iperbole di equazione
9x2 - 4y2 = 36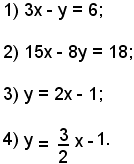
Le coordinate dei punti di intersezione dell'iperbole con una retta devono soddisfare le equazioni dell'iperbole e della retta; esse sono perciò le soluzioni del sistema formato dalle equazioni dell'iperbole e della retta.
1) Le coordinate dei punti di intersezione dell'iperbole 9x2 - 4y2 = 36 con la retta 3x - y = 6 sono date dalle soluzioni del sistema:
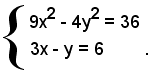
Ricavando la y dalla seconda equazione e sostituendo nella prima, si ha
3x2 - 6x + 20 = 0,
da cui
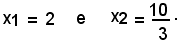
Sostituendo tali valori nell'equazione della retta, si ottiene:
y1 = 0 e y2 = 4 .
La retta è secante l'iperbole nei punti
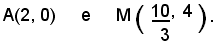
2) Le coordinate dei punti di intersezione dell'iperbole 9x2 - 4y2 = 36 con la retta 15x - 8y = 18, sono date dalle soluzioni del sistema:
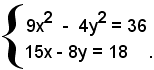
Ricavando la y dalla seconda equazione e sostituendo nella prima, si ha
9x2 - 60x + 100 = 0,
da cui
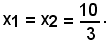
Sostituendo tali valori nell'equazione della retta, si ottiene:
y1 = y2 = 4 .
La retta è tangente all'iperbole nei punto
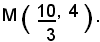
3) Le coordinate dei punti di intersezione dell'iperbole 9x2 - 4y2 = 36 con la retta y = 2x - 1, sono date dalle soluzioni del sistema:
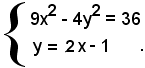
Le ascisse dei punti di intersezione sono immaginarie; sostituendo tali valori nella seconda equazione del sistema, si trovano le ordinate, anch'esse immaginarie. La retta y = 2x - 1 è dunque esterna all'iperbole.
4) Le coordinate dei punti di intersezione dell'iperbole 9x2 - 4y2 = 36 con la retta 4), sono date dalle soluzioni del sistema:
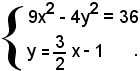
Sostituendo il valore della y, della seconda equazione, nella prima, si ha:
3x - 10 = 0,
cioè
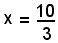
e, sostituendo tale valore nella seconda equazione del sistema, si ottiene:
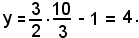
Quindi la retta 4) incontra l'iperbole nel punto
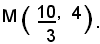
L'equazione risultante dal sistema 3x - 10 = 0 si è abbassata di grado, dal secondo al primo, e si è così persa una soluzione. Analiticamente si sa che quando un'equazione si abbassa di grado, una soluzione va all'infinito. D'altra parte, geometricamente si rileva come la retta 4) sia parallela all'asintoto y = 3/2, e poichè questo è tangente all'iperbole all'infinito e poichè due rette parallele hanno lo stesso punto all'infinito, la retta 4) incontra l'iperbole nel punto all'infinito dell'asintoto. Tale proprietà vale per qualsiasi retta parallela ad un asintoto di un'iperbole.
Si ha, dunque:
-una retta parallela ad un asintoto incontra l'iperbole in un punto proprio e nel punto all'infinito dell'asintoto.
Si chiama punto proprio un punto al finito.
Si chiama punto improprio un punto all'infinito.
Nota bene
Due rette incidenti si incontrano in un punto proprio; due rette parallele si incontrano in un punto improprio.
In tal modo due rette complanari hanno sempre un punto in comune:
proprio, se incidenti;
improprio, se parallele.
Retta tangente all'iperbole in un suo punto
Data l'iperbole di equazione
16x2 - 9y2 = 144
e un suo punto P di coordinate 15/4 e 3, si vuole determinare l'equazione della retta tangente all'iperbole in tale punto.
Primo procedimento
Si considera una retta generica passante per il punto P; essa ha equazione:
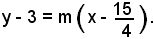
Le coordinate dei punti di intersezione retta-iperbole si trovano risolvendo il sistema:
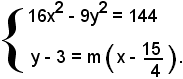
Ricavando la y dalla seconda equazione e sostituendo nella prima, si ha:
Affinchè la retta considerata sia tangente all'iperbole nel punto P, occorre che le due intersezioni retta-iperbole coincidano in P, cioè che le radici dell'equazione precedente, che forniscono le ascisse dei punti comuni all'iperbole e alla retta, siano reali e coincidenti, cioè il discriminante Δ della a) sia uguale a zero, cioè:
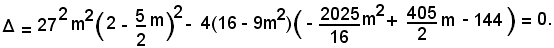
Sviluppando e semplificando, si ha:
81m2 - 360m + 400 = 0,
da cui
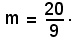
Sostituendo tale valore nell'equazione della retta generica inizialmente considerata, si ottiene:
b) 20x - 9y - 48 = 0,
chè è l'equazione della retta tangente richiesta.
Secondo procedimento - Formula di sdoppiamento
La b) si può ottenere direttamente applicando la formula di sdoppiamento, cioè sostituendo nell'equazione dell'iperbole 6x2 - 9y2 = 144 ad x2 il valore (15/4)x, prodotto dell'ascissa 15/4 del punto P per la variabile x, e ad y2 il valore 3·y, prodotto dell'ordinata 3 del punto P per la variabile y.
Infatti, si ha:
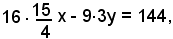
cioè
60x - 27y - 144 = 0
e dividendo per 3, si ottiene
20x - 9y - 48 = 0.
In generale, l'equazione della tangente all'iperbole
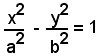
nel punto P(x0, y0) si ottiene sostituendo nell'equazione della curva, ad x2 il valore xx0, e ad y2 il valore yy0. La retta tangente all'iperbole nel punto P(x0, y0) ha dunque equazione:
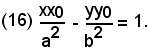
Se il punto P(x0, y0) non appartiene all'iperbole, la retta
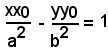
si chiama polare del punto P rispetto all'iperbole.
Essa rappresenta la retta congiungente i punti di contatto delle due tangenti condotte dal punto P all'iperbole.
Le proprietà relative alla polarità rispetto all'ellisse valgono anche per l'iperbole.
Retta normale all'iperbole in un suo punto
La retta normale all'iperbole in un suo punto è la retta perpendicolare in quel punto alla tangente all'iperbole.
Si consideri l'iperbole di equazione:
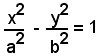
e un suo punto P(x0, y0).
In precedenza si è determinata l'equazione della tangente all'iperbole nel punto P(x0, y0), il cui coefficiente angolare ha valore:
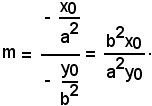
Per scrivere l'equazione della normale in P all'iperbole, sia y -y0 = m(x - x0) l'equazione di una retta generica per il punto P(x0, y0).
Tale retta è perpendicolare alla (16) se il suo coefficiente angolare m' è uguale all'inverso e reciproco di m, cioè:
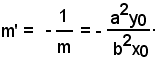
Dunque, l'equazione della normale in P(x0, y0) all'iperbole
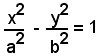
è
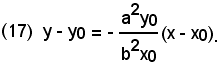
Esempio
Scrivere l'equazione della normale all'iperbole 16x2 - 9y2 = 144 nel punto
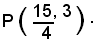
Si scrive l'equazione della retta generica
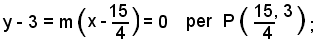
si ora determina, come si è visto in precedenza, l'equazione della tangente all'iperbole nel punto P, che risulta
20x - 9y - 48 = 0.
Il coefficiente angolare della tangente è:
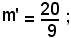
il coefficiente angolare m della dev'essere uguale all'opposto e reciproco di m', quindi è:
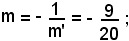
sostituendo tale valore nella
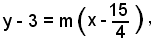
si ottiene l'equazione della normale richiesta
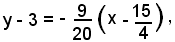
cioè
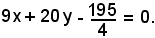
Proprietà importanti dell'iperbole
1)-In un'iperbole il punto medio del segmento staccato dagli asintoti su una retta secante è anche punto medio della relativa corda.
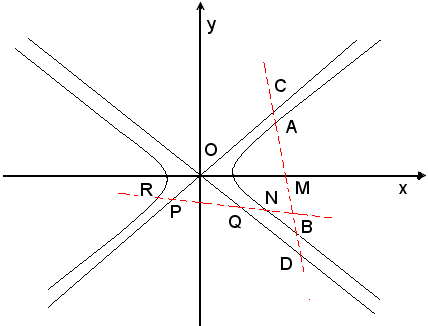
Si vuole ora dimostrare che il punto medio M del segmento CD è anche punto medio della corda AB, ossia i segmenti BD e AC sono uguali, come sono uguali i segmenti RP e QN.
Sia
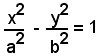
l'equazione dell'iperbole e
y = mx + q
l'equazione di una retta qualsiasi del piano.
Le coordinate dei punti C e D si ottengono risolvendo rispettivamente i sistemi seguenti:
Si ha:
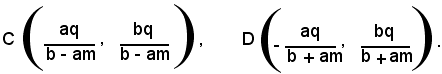
Le coordinate del punto medio M del segmento CD sono date da:
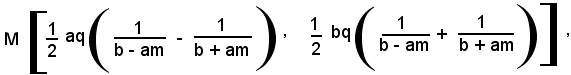
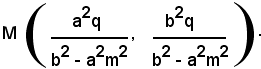
Le coordinate dei punti A e B, intersezioni della retta y = mx + q con l'iperbole, sono date dalle soluzioni del sistema:
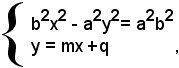
da cui si ricava l'equazione risultante del sistema:
(b2 - a2m2)x2 - 2a2mqx - a2(q2 + b2) = 0 .
Le coordinate del punto medio M della corda AB sono date da:
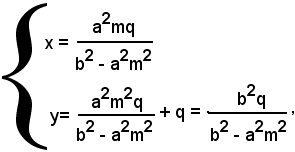
Si ricordi che l'equazione risultante del sistema fornisce le ascisse dei punti A e B, intersezioni della retta con l'iperbole. L'ascissa del punto medio è data dalla semisomma delle radici dell'equazione risultante. Si ricordi inoltre che, data l'equazione ax2 + bx + c = 0, risulta:
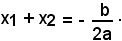
2)-Il punto di contatto di una tangente all'iperbole è il punto medio del segmento staccato sulla tangente dagli asintoti.
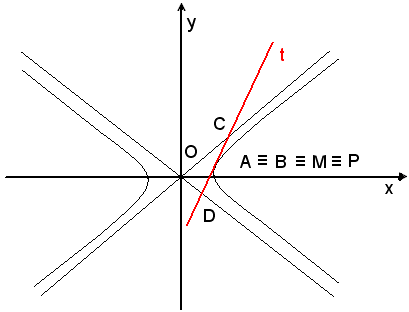
Questa proprietà è un caso particolare della precedente.
Infatti, nel caso in cui i punti A e B coincidano, la retta AB risulta tangente all'iperbole nel punto A ≡ B ≡ M.
Allo scopo, sia
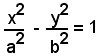
l'equazione dell'iperbole e, come già visto,
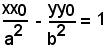
l'equazione della tangente t in P(x0, y0) alla curva. Le coordinate dei punti di intersezione C e D della tangente t con gli asintoti sono date rispettivamente dalle soluzioni dei sistemi:
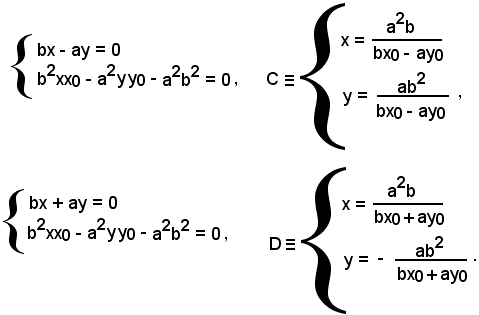
Le coordinate del punto medio M della corda AB sono date da:
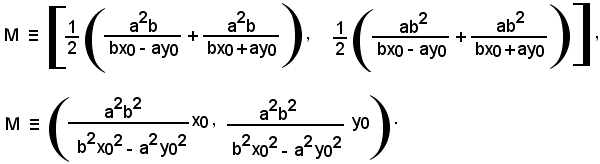
Affinchè il punto P(x0, y0) appartenga all'iperbole, occorre che le coordinate x0 e y0 soddisfino l'equazione, cioè si verifichi:
b2x020 - a2y02 = a2b2.
Sostituendo al denominatore delle coordinate di M il valore a2b2 si ha:
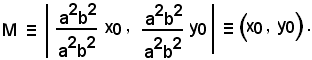
asintoti.
Si indicano con x e y le rette, asintoti, x + y = 0 e x - y = 0 e si fanno ruotare di un angolo di (- 45°) gli assi x ed y intorno all'origine 0. Sostituendo nella (10) ad x ed y rispettivamente:
x = Xcos(-45°) - Ysen(-45°),
y = Xsen(-45°) + Ycos(-45°),
e ciò ricordando le formule di rotazione degli assi e che
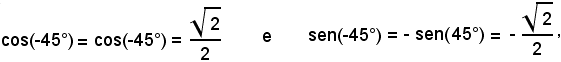
risulta
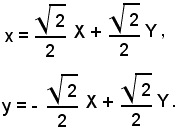
si ha
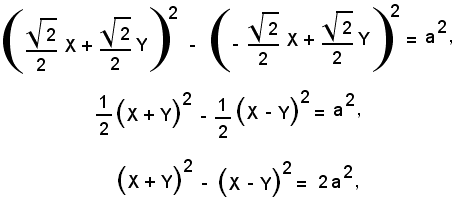
ossia
2XY + 2XY = 2a2,
4XY = 2a2,
cioè
La (12) rappresenta l'equazione dell'iperbole equilatera riferita agli asintoti.
Viceversa, ogni equazione del tipo (13) xy = k rappresenta un'iperbole equilatera che ha gli assi cartesiani come asintoti.
In generale, l'equazione di un'iperbole riferita agli asintoti di equazioni
ax + by + c = 0 e a'x + b'y + c' = 0
è
(ax + by + c)(a'x + b'y + c') = k.
Se k > 0, l'asse trasverso dell'iperbole (13) è la bisettrice del primo e del terzo quadrante ed ha per lunghezza
.Se k < 0, l'asse trasverso dell'iperbole (13) è la bisettrice del secondo e del quarto quadrante ed ha per lunghezza
.Un'iperbole equilatera avente come asintoti le rette
x - a = 0 e y - b = 0,
e quindi avente centro C (a, b), ha equazione del tipo:
(x - a)(y - b) = k,
sviluppando
xy - bx - ay + ab - k = 0
e posto
ab - k = c
risulta
(14) xy
- bx - ay + c = 0.
Viceversa, qualunque equazione del tipo (1) rappresenta un'iperbole equilatera di centro C(a, b) ed avente per asintoti le rette x - a = 0 e y - b = 0.
L'equazione (14), risolta rispetto alla y diventa:
Si può quindi affermare che, qualsiasi equazione del tipo
con mq≠np, rappresenta un'iperbole avente per centro
e per asintoti le rette
Se mq = np, l'equazione (15) rappresenta la retta
Infatti, da mq = np, si ha che
Esempio
Scrivere l'equazione dell'iperbole equilatera avente per asintoti gli assi cartesiani e passante per il punto P(1, 2). L'equazione dell'iperbole è del tipo xy = k.
Affinchè la curva passi per P, le coordinate 1 e 2 devono soddisfare l'equazione, cioè dev'essere:
1 · 2 = k,
da cui
k = 2.
L'equazione dell'iperbole richiesta è
I semiassi hanno lunghezza
la distanza focale
Intersezioni dell'iperbole con delle rette
Determinare le intersezioni dell'iperbole di equazione
9x2 - 4y2 = 36
con le rette di equazioni:
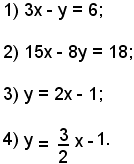
Le coordinate dei punti di intersezione dell'iperbole con una retta devono soddisfare le equazioni dell'iperbole e della retta; esse sono perciò le soluzioni del sistema formato dalle equazioni dell'iperbole e della retta.
1) Le coordinate dei punti di intersezione dell'iperbole 9x2 - 4y2 = 36 con la retta 3x - y = 6 sono date dalle soluzioni del sistema:
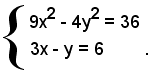
Ricavando la y dalla seconda equazione e sostituendo nella prima, si ha
3x2 - 6x + 20 = 0,
da cui
Sostituendo tali valori nell'equazione della retta, si ottiene:
y1 = 0 e y2 = 4 .
La retta è secante l'iperbole nei punti
2) Le coordinate dei punti di intersezione dell'iperbole 9x2 - 4y2 = 36 con la retta 15x - 8y = 18, sono date dalle soluzioni del sistema:
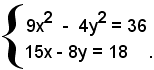
Ricavando la y dalla seconda equazione e sostituendo nella prima, si ha
9x2 - 60x + 100 = 0,
da cui
Sostituendo tali valori nell'equazione della retta, si ottiene:
y1 = y2 = 4 .
La retta è tangente all'iperbole nei punto
3) Le coordinate dei punti di intersezione dell'iperbole 9x2 - 4y2 = 36 con la retta y = 2x - 1, sono date dalle soluzioni del sistema:
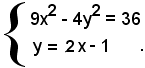
Ricavando la y dalla seconda equazione e sostituendo nella prima, si ha
7x2 - 16x + 40 = 0,
da cui
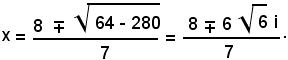
7x2 - 16x + 40 = 0,
da cui
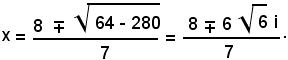
Le ascisse dei punti di intersezione sono immaginarie; sostituendo tali valori nella seconda equazione del sistema, si trovano le ordinate, anch'esse immaginarie. La retta y = 2x - 1 è dunque esterna all'iperbole.
4) Le coordinate dei punti di intersezione dell'iperbole 9x2 - 4y2 = 36 con la retta 4), sono date dalle soluzioni del sistema:
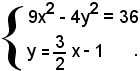
Sostituendo il valore della y, della seconda equazione, nella prima, si ha:
cioè
e, sostituendo tale valore nella seconda equazione del sistema, si ottiene:
Quindi la retta 4) incontra l'iperbole nel punto
L'equazione risultante dal sistema 3x - 10 = 0 si è abbassata di grado, dal secondo al primo, e si è così persa una soluzione. Analiticamente si sa che quando un'equazione si abbassa di grado, una soluzione va all'infinito. D'altra parte, geometricamente si rileva come la retta 4) sia parallela all'asintoto y = 3/2, e poichè questo è tangente all'iperbole all'infinito e poichè due rette parallele hanno lo stesso punto all'infinito, la retta 4) incontra l'iperbole nel punto all'infinito dell'asintoto. Tale proprietà vale per qualsiasi retta parallela ad un asintoto di un'iperbole.
Si ha, dunque:
-una retta parallela ad un asintoto incontra l'iperbole in un punto proprio e nel punto all'infinito dell'asintoto.
Si chiama punto proprio un punto al finito.
Si chiama punto improprio un punto all'infinito.
Nota bene
Due rette incidenti si incontrano in un punto proprio; due rette parallele si incontrano in un punto improprio.
In tal modo due rette complanari hanno sempre un punto in comune:
proprio, se incidenti;
improprio, se parallele.
Retta tangente all'iperbole in un suo punto
Data l'iperbole di equazione
16x2 - 9y2 = 144
e un suo punto P di coordinate 15/4 e 3, si vuole determinare l'equazione della retta tangente all'iperbole in tale punto.
Primo procedimento
Si considera una retta generica passante per il punto P; essa ha equazione:
Le coordinate dei punti di intersezione retta-iperbole si trovano risolvendo il sistema:
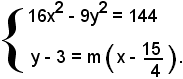
Ricavando la y dalla seconda equazione e sostituendo nella prima, si ha:
Affinchè la retta considerata sia tangente all'iperbole nel punto P, occorre che le due intersezioni retta-iperbole coincidano in P, cioè che le radici dell'equazione precedente, che forniscono le ascisse dei punti comuni all'iperbole e alla retta, siano reali e coincidenti, cioè il discriminante Δ della a) sia uguale a zero, cioè:
Sviluppando e semplificando, si ha:
81m2 - 360m + 400 = 0,
da cui
Sostituendo tale valore nell'equazione della retta generica inizialmente considerata, si ottiene:
b) 20x - 9y - 48 = 0,
chè è l'equazione della retta tangente richiesta.
Secondo procedimento - Formula di sdoppiamento
La b) si può ottenere direttamente applicando la formula di sdoppiamento, cioè sostituendo nell'equazione dell'iperbole 6x2 - 9y2 = 144 ad x2 il valore (15/4)x, prodotto dell'ascissa 15/4 del punto P per la variabile x, e ad y2 il valore 3·y, prodotto dell'ordinata 3 del punto P per la variabile y.
Infatti, si ha:
cioè
60x - 27y - 144 = 0
e dividendo per 3, si ottiene
20x - 9y - 48 = 0.
In generale, l'equazione della tangente all'iperbole
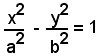
nel punto P(x0, y0) si ottiene sostituendo nell'equazione della curva, ad x2 il valore xx0, e ad y2 il valore yy0. La retta tangente all'iperbole nel punto P(x0, y0) ha dunque equazione:
Se il punto P(x0, y0) non appartiene all'iperbole, la retta
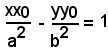
si chiama polare del punto P rispetto all'iperbole.
Essa rappresenta la retta congiungente i punti di contatto delle due tangenti condotte dal punto P all'iperbole.
Le proprietà relative alla polarità rispetto all'ellisse valgono anche per l'iperbole.
Retta normale all'iperbole in un suo punto
La retta normale all'iperbole in un suo punto è la retta perpendicolare in quel punto alla tangente all'iperbole.
Si consideri l'iperbole di equazione:
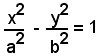
e un suo punto P(x0, y0).
In precedenza si è determinata l'equazione della tangente all'iperbole nel punto P(x0, y0), il cui coefficiente angolare ha valore:
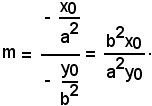
Per scrivere l'equazione della normale in P all'iperbole, sia y -y0 = m(x - x0) l'equazione di una retta generica per il punto P(x0, y0).
Tale retta è perpendicolare alla (16) se il suo coefficiente angolare m' è uguale all'inverso e reciproco di m, cioè:
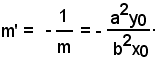
Dunque, l'equazione della normale in P(x0, y0) all'iperbole
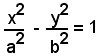
è
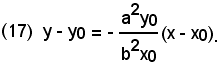
Esempio
Scrivere l'equazione della normale all'iperbole 16x2 - 9y2 = 144 nel punto
Si scrive l'equazione della retta generica
si ora determina, come si è visto in precedenza, l'equazione della tangente all'iperbole nel punto P, che risulta
20x - 9y - 48 = 0.
Il coefficiente angolare della tangente è:
il coefficiente angolare m della dev'essere uguale all'opposto e reciproco di m', quindi è:
sostituendo tale valore nella
si ottiene l'equazione della normale richiesta
cioè
Proprietà importanti dell'iperbole
1)-In un'iperbole il punto medio del segmento staccato dagli asintoti su una retta secante è anche punto medio della relativa corda.
Si vuole ora dimostrare che il punto medio M del segmento CD è anche punto medio della corda AB, ossia i segmenti BD e AC sono uguali, come sono uguali i segmenti RP e QN.
Sia
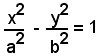
l'equazione dell'iperbole e
y = mx + q
l'equazione di una retta qualsiasi del piano.
Le coordinate dei punti C e D si ottengono risolvendo rispettivamente i sistemi seguenti:
Si ha:
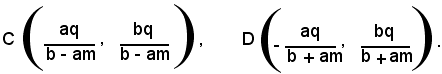
Le coordinate del punto medio M del segmento CD sono date da:
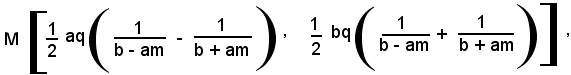
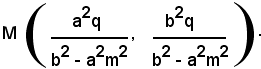
Le coordinate dei punti A e B, intersezioni della retta y = mx + q con l'iperbole, sono date dalle soluzioni del sistema:
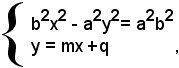
da cui si ricava l'equazione risultante del sistema:
(b2 - a2m2)x2 - 2a2mqx - a2(q2 + b2) = 0 .
Le coordinate del punto medio M della corda AB sono date da:
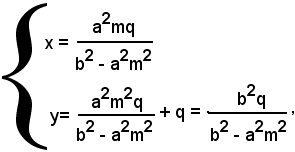
Si ricordi che l'equazione risultante del sistema fornisce le ascisse dei punti A e B, intersezioni della retta con l'iperbole. L'ascissa del punto medio è data dalla semisomma delle radici dell'equazione risultante. Si ricordi inoltre che, data l'equazione ax2 + bx + c = 0, risulta:
2)-Il punto di contatto di una tangente all'iperbole è il punto medio del segmento staccato sulla tangente dagli asintoti.
Questa proprietà è un caso particolare della precedente.
Infatti, nel caso in cui i punti A e B coincidano, la retta AB risulta tangente all'iperbole nel punto A ≡ B ≡ M.
Allo scopo, sia
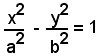
l'equazione dell'iperbole e, come già visto,
l'equazione della tangente t in P(x0, y0) alla curva. Le coordinate dei punti di intersezione C e D della tangente t con gli asintoti sono date rispettivamente dalle soluzioni dei sistemi:
Le coordinate del punto medio M della corda AB sono date da:
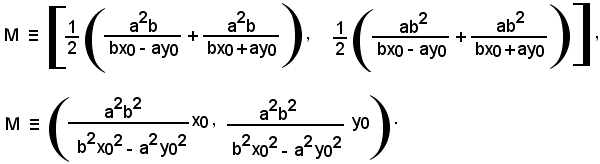
Affinchè il punto P(x0, y0) appartenga all'iperbole, occorre che le coordinate x0 e y0 soddisfino l'equazione, cioè si verifichi:
b2x020 - a2y02 = a2b2.
Sostituendo al denominatore delle coordinate di M il valore a2b2 si ha:
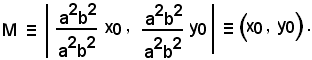
Quindi, il punto medio M coincide con il punto P.
3)-Il triangolo formato dagli asintoti e da una tangente all'iperbole ha area costante al variare della tangente stessa.
L'area del triangolo COD è data dal semiprodotto della base OD per l'altezza h = CR, ove h rappresenta la distanza del punto C dalla retta OD, asintoto, di equazione bx + ay = 0.
Le coordinate dei punti C e D sono date, come già visto, da:
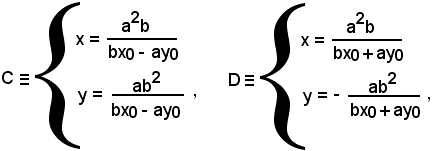
per cui:
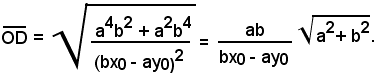
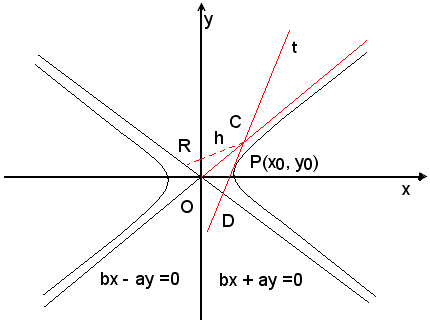
La distanza del punto C dall'asintoto OD, di equazione bx + ay = 0, come si è visto in precedenza, è data da:
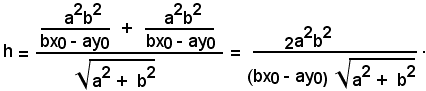
L'area del triangolo OCD risulta:
Poichè b2x02 - a2y02 = a2b2 è la condizione necessaria e sufficiente affinchè P(x0, y0) appartenga all'iperbole, sostituendo nella relazione precedente a2b2 al posto di b2x02 - a2y02, si ricava:
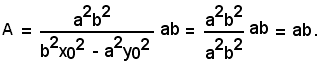
Dunque: l'area del triangolo DOC, formato dagli asintoti e da una tangente all'iperbole, è uguale al prodotto ab dei semiassi dell'iperbole e perciò è costante al variare della tangente.
Viceversa, ogni retta che forma con l'angolo completo degli asintoti, contenente l'iperbole, un triangolo di area ab, è una tangente all'iperbole.
COMPLEMENTI
Tangente e normale all'iperbole in un suo punto
La tangente e la normale all'iperbole in un suo punto sono le bisettrici degli angoli formati dalle rette che congiungono quei punti con i fuochi.
La dimostrazione è analoga a quella dell'ellisse.
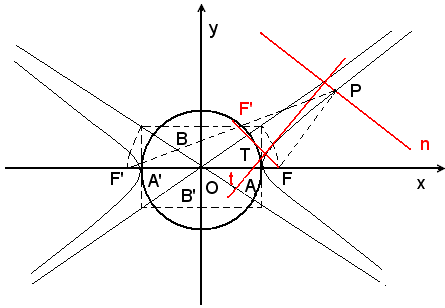
Si osservi come la tangente all'iperbole in un punto P sia la bisettrice dell'angolo
,
e quindi taglia il segmento FF', mentre la tangente all'ellisse
è la bisettrice esterna dello stesso angolo. Esistono, dunque,
un'ellisse ed un'iperbole aventi fuochi dati F e F' e passanti per P;
le tangenti ad esse sono perpendicolari.
Esempio
Data l'iperbole di equazione
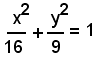
ed il suo punto
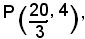
verificare
che la tangente e la normale in P alla curva sono le bisettrici degli
angoli formati dalle rette che congiungono il punto
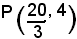
con i fuochi F(5, 0) e F'(-5, 0).
Le rette PF, PF' hanno rispettivamente equazioni:
12x - 5y - 60 = 0 e 12x - 35y - 60 = 0.
Le equazioni delle bisettrici degli angoli formati dalle due rette sono:
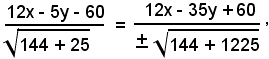
cioè
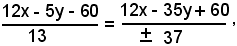
ossia
è
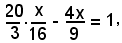
ossia
c) 15x - 16y - 36 = 0;
L'equazione della normale in P alla curva è data da:
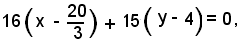
ossia
d) 48x + 45y - 500 = 0.
Le equazioni c) e d) coincidono rispettivamente con a) e b), come volevasi dimostrare.
Podaria dei fuochi rispetto all'iperbole
La podaria dei fuochi rispetto ad un'iperbole è il cerchio che ha per diametro l'asse trasverso AA'.
La dimostrazione di questa proprietà è analoga a quella dell'ellisse.
Esempio
Verificare che il piede dalla perpendicolare condotta dal fuoco F(5, 0) all'iperbole
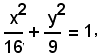
alla tangente alla curva nel punto
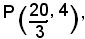
appartiene al cerchio di centro O e raggio 4, podaria dei fuochi rispetto all'iperbole.
In generale, trovare analiticamente l'equazione della podaria del fuoco F(c, 0) rispetto all'iperbole
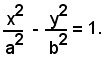
Se P(x0, y0) è un punto dell'iperbole, l'equazione della tangente in P(x0, y0) è:
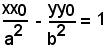
e l'equazione della perpendicolare a questa condotta per il fuoco F è:
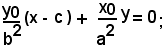
le coordinate del punto T, piede della perpendicolare condotta da F alla tangente in P, sono date dalla soluzione del sistema formato dalle due equazioni:
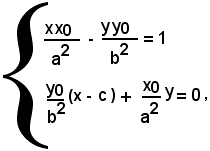
ove x0 ed y0 devono soddisfare la condizione:
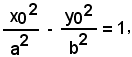
essendo P un punto dell'iperbole.
L'equazione del luogo dei punti T si ottiene eliminando x0 ed y0 dalle tre equazioni precedenti. Allo scopo, si risolve il sistema formato dalle prime due equazioni rispetto ad x0 ed y0, e si sostituiscono tali valori nell'ultima equazione scritta. In tal modo si ottiene :
x2 + y2 - a2 = 0,
equazione del cerchio podaria.
La tangente alla curva nel punto
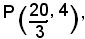
ha equazione 15x - 16y - 36 = 0, la perpendicolare a questa per F(5, 0) è data da 16x + 15y - 80 = 0. Le coordinate del punto T, piede della perpendicolare condotta da F alla tangente in P all'iperbole, sono date dalla soluzione del sistema formato dalle due equazioni precedenti:
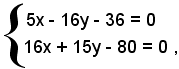
cioè
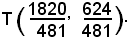
L'equazione del cerchio di centro O e raggio 4 è:
x2 + y2 = 16;
essa è soddisfatta dalle coordinate di T.
Infatti, si ha:
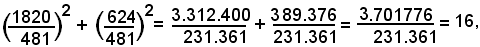
come volevasi dimostrare.
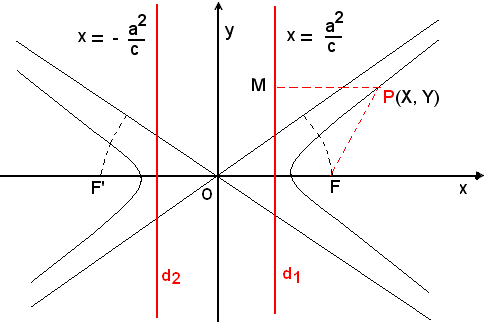
Direttrice - Eccentricità
Analogamente al caso dell'ellisse, si definiscono direttrici dell'iperbole relative ai fuochi F(c, 0) e F'(-c, 0), le rette d1 e d2 perpendicolari all'asse trasverso di equazioni:
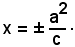
Come l'ellisse si riconosce che:
-per i punti dell'iperbole è costante il rapporto delle distanze da un fuoco F o F', e dalla relativa direttrice d1, d2, e che tale rapporto è uguale a c/a.
Siano x ed y le coordinate di un punto qualsiasi P del piano, la distanza di P dal fuoco F è:
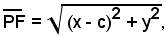
la distanza di P dalla retta
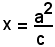
è
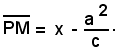
Se il punto P soddisfa la relazione
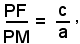
esso appartiene all'iperbole
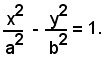
Traducendo analiticamente la relazione precedente, si ricava:
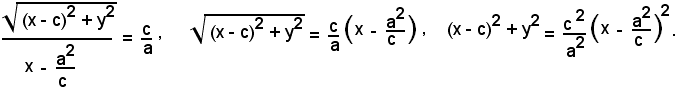
Sviluppando, riducendo ed ordinando, si ottiene:
(a2 - c2)x2 + a2y2 = a2(a2 - c2);
poichè a2 - c2 = - b2, si ricava infine
b2x2 - a2y2 = a2b2
e dividendo per a2b2, si ottiene
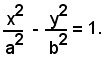
Questa è la condizione necessaria e sufficiente affinchè il punto P appartenga all'iperbole.
Le proprietà enunciate permettono le seguenti costruzioni:
1)-costruire per punti un'iperbole, dati gli asintoti ed un punto.
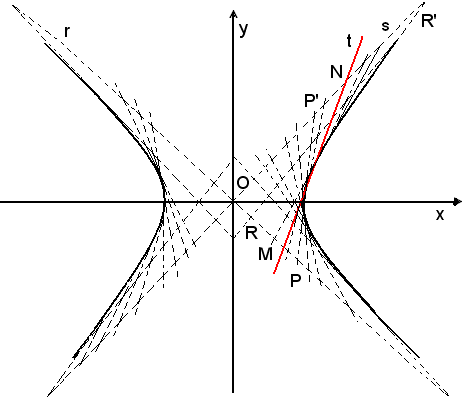
Siano r ed s gli asintoti e P un punto. Si conduce per P la retta generica m e siano C e D le intersezioni con gli asintoti. Per la prima proprietà enunciata, l'ulteriore intersezione Q di m con l'iperbole dev'essere tale che PD = CQ. Il punto Q si determina portando sulla retta CD, a partire dal punto C un segmento uguale a PD. Ripetendo la costruzione si trovano altri punti dell'iperbole. In figura sono indicate le costruzioni dei punti M e R.
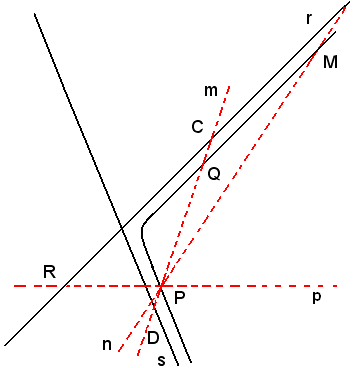
2)-Costruire per tangenti un'iperbole, dati gli asintoti ed una tangente.
Siano r e s gli asintoti e t la tangente data; si indicano con M e N i punti di intersezione dalla tangente con gli asintoti.
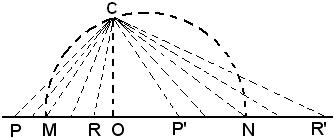
Per la terza proprietà, per costruire altre tangenti all'iperbole, occorre costruire rette che formano con gli asintoti, nell'angolo completo in cui è contenuta la curva, triangoli equivalenti al triangolo MON. Poichè i triangoli devono avere un vertice in O, è sufficiente costruire rette che staccano sugli asintoti coppie di segmenti aventi prodotto uguale al prodotto dei segmenti staccati sugli asintoti dalla tangente data. Allo scopo, si riportano successivamente su una retta r i segmenti MO e ON, si costruisce la semicirconferenza di diametro MN e si conduce per O la perpendicolare alla r, che incontra la semicirconferenza in C. Per il teorema di Euclide, si ha:
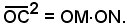
Per costruire altre tangenti all'iperbole, si prende sulla retta r un punto P e si determina P', intersezione della perpendicolare in C alla retta PC con la r; si riporta sull'asintoto r, a partire da O, il segmento OP e sull'asintoto s il segmento OP'. La retta tangente PP' è una tangente all'iperbole. Infatti, si ha:
Facendo variare il punto P sulla retta r e con la costruzione suddetta, si determinano le tangenti all'iperbole nel numero desiderato.
Nota bene
Per la seconda proprietà è noto che il punto medio del segmento intercettato siulla tangente dagli asintoti è il punto di contatto, in modo che, determinando di ogni tangente il punto di contatto, può costruirsi l'iperbole luogo di punti.
3)-Data l'iperbole mediante gli asintoti r, s ed un punto P, costruire la tangente all'iperbole in P.
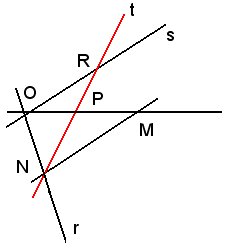
Si congiunge P con O e si porta su questa retta il segmento PM = OP, per M la parallela all'asintoto s fino ad incontrare in N l'asintoto r; la congiungente NP è la tangente richiesta.
Infatti, indicando con R l'intersezione di dalla t con l'asintoto s, i triangoli NMP e OPR sono uguali perchè hanno OP = PM per costruzione, gli angoli in P uguali, perchè opposti al vertice, l'angolo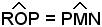
,
perchè alterni interni, quindi PN = RP. Il punto P è,
dunque, il punto medio del segmento RN; segue che la retta RN è
la tangente all'iperbole nel punto P.
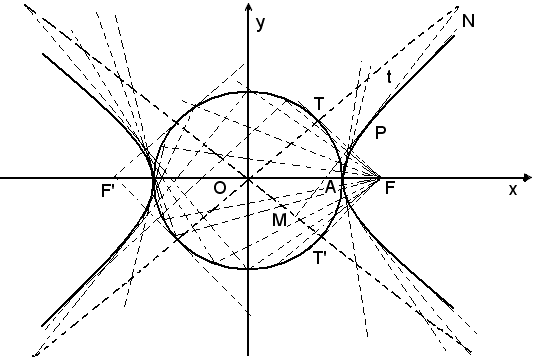
4)-Costruire per tangenti un'iperbole di cui siano dati i fuochi F e F' ed il cerchio podaria.
Il cerchio podaria dell'iperbole è il cerchio di centro O avente come raggio il semiasse trasverso a. Per costruire la curva, si conducono dal fuoco F rette secanti il cerchio e dai punti di intersezioni le perpendicolari ad esse. Tali perpendicolari rappresentano tangenti all'iperbole. I punti di contatto delle tangenti sono dati dai punti medi dei segmenti staccati su di esse dagli asintoti. In figura è determinato il punto di contatto P della tangente t; esso è il punto medio del segmento MN. Gli asintoti, unica coppia di tangenti all'iperbole passanti per il centro, si ottengono congiungendo il centro del cerchio con i punti di contatto T e T' delle tangenti condotte da F al cerchio podaria.
3)-Il triangolo formato dagli asintoti e da una tangente all'iperbole ha area costante al variare della tangente stessa.
L'area del triangolo COD è data dal semiprodotto della base OD per l'altezza h = CR, ove h rappresenta la distanza del punto C dalla retta OD, asintoto, di equazione bx + ay = 0.
Le coordinate dei punti C e D sono date, come già visto, da:
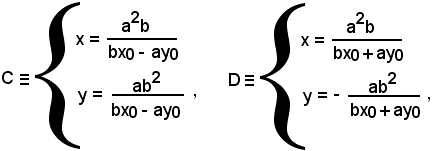
per cui:
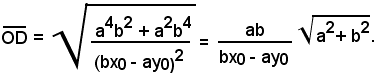
La distanza del punto C dall'asintoto OD, di equazione bx + ay = 0, come si è visto in precedenza, è data da:
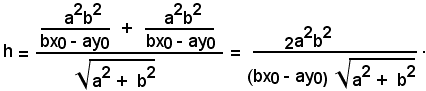
L'area del triangolo OCD risulta:
Poichè b2x02 - a2y02 = a2b2 è la condizione necessaria e sufficiente affinchè P(x0, y0) appartenga all'iperbole, sostituendo nella relazione precedente a2b2 al posto di b2x02 - a2y02, si ricava:
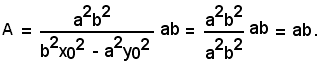
Dunque: l'area del triangolo DOC, formato dagli asintoti e da una tangente all'iperbole, è uguale al prodotto ab dei semiassi dell'iperbole e perciò è costante al variare della tangente.
Viceversa, ogni retta che forma con l'angolo completo degli asintoti, contenente l'iperbole, un triangolo di area ab, è una tangente all'iperbole.
COMPLEMENTI
Tangente e normale all'iperbole in un suo punto
La tangente e la normale all'iperbole in un suo punto sono le bisettrici degli angoli formati dalle rette che congiungono quei punti con i fuochi.
La dimostrazione è analoga a quella dell'ellisse.
Si osservi come la tangente all'iperbole in un punto P sia la bisettrice dell'angolo
,
e quindi taglia il segmento FF', mentre la tangente all'ellisse
è la bisettrice esterna dello stesso angolo. Esistono, dunque,
un'ellisse ed un'iperbole aventi fuochi dati F e F' e passanti per P;
le tangenti ad esse sono perpendicolari. Esempio
Data l'iperbole di equazione
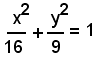
ed il suo punto
con i fuochi F(5, 0) e F'(-5, 0).
Le rette PF, PF' hanno rispettivamente equazioni:
12x - 5y - 60 = 0 e 12x - 35y - 60 = 0.
Le equazioni delle bisettrici degli angoli formati dalle due rette sono:
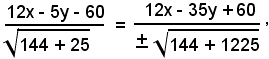
cioè
ossia
a) 48x + 45y - 500 = 0, b) 15x - 16y - 36 = 0.
L'equazione della tangente all'iperbole nel punto
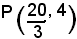
L'equazione della tangente all'iperbole nel punto
è
ossia
c) 15x - 16y - 36 = 0;
L'equazione della normale in P alla curva è data da:
ossia
d) 48x + 45y - 500 = 0.
Le equazioni c) e d) coincidono rispettivamente con a) e b), come volevasi dimostrare.
Podaria dei fuochi rispetto all'iperbole
La podaria dei fuochi rispetto ad un'iperbole è il cerchio che ha per diametro l'asse trasverso AA'.
La dimostrazione di questa proprietà è analoga a quella dell'ellisse.
Esempio
Verificare che il piede dalla perpendicolare condotta dal fuoco F(5, 0) all'iperbole
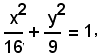
alla tangente alla curva nel punto
appartiene al cerchio di centro O e raggio 4, podaria dei fuochi rispetto all'iperbole.
In generale, trovare analiticamente l'equazione della podaria del fuoco F(c, 0) rispetto all'iperbole
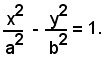
Se P(x0, y0) è un punto dell'iperbole, l'equazione della tangente in P(x0, y0) è:
e l'equazione della perpendicolare a questa condotta per il fuoco F è:
le coordinate del punto T, piede della perpendicolare condotta da F alla tangente in P, sono date dalla soluzione del sistema formato dalle due equazioni:
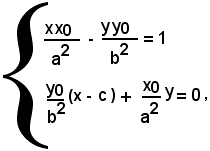
ove x0 ed y0 devono soddisfare la condizione:
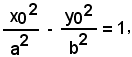
essendo P un punto dell'iperbole.
L'equazione del luogo dei punti T si ottiene eliminando x0 ed y0 dalle tre equazioni precedenti. Allo scopo, si risolve il sistema formato dalle prime due equazioni rispetto ad x0 ed y0, e si sostituiscono tali valori nell'ultima equazione scritta. In tal modo si ottiene :
x2 + y2 - a2 = 0,
equazione del cerchio podaria.
La tangente alla curva nel punto
ha equazione 15x - 16y - 36 = 0, la perpendicolare a questa per F(5, 0) è data da 16x + 15y - 80 = 0. Le coordinate del punto T, piede della perpendicolare condotta da F alla tangente in P all'iperbole, sono date dalla soluzione del sistema formato dalle due equazioni precedenti:
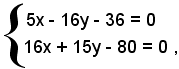
cioè
L'equazione del cerchio di centro O e raggio 4 è:
x2 + y2 = 16;
essa è soddisfatta dalle coordinate di T.
Infatti, si ha:
come volevasi dimostrare.
Direttrice - Eccentricità
Analogamente al caso dell'ellisse, si definiscono direttrici dell'iperbole relative ai fuochi F(c, 0) e F'(-c, 0), le rette d1 e d2 perpendicolari all'asse trasverso di equazioni:
Come l'ellisse si riconosce che:
-per i punti dell'iperbole è costante il rapporto delle distanze da un fuoco F o F', e dalla relativa direttrice d1, d2, e che tale rapporto è uguale a c/a.
Siano x ed y le coordinate di un punto qualsiasi P del piano, la distanza di P dal fuoco F è:
la distanza di P dalla retta
è
Se il punto P soddisfa la relazione
esso appartiene all'iperbole
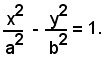
Traducendo analiticamente la relazione precedente, si ricava:
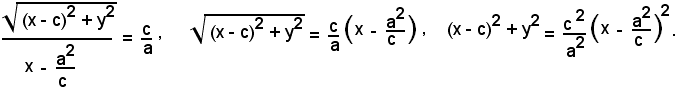
Sviluppando, riducendo ed ordinando, si ottiene:
(a2 - c2)x2 + a2y2 = a2(a2 - c2);
poichè a2 - c2 = - b2, si ricava infine
b2x2 - a2y2 = a2b2
e dividendo per a2b2, si ottiene
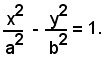
Questa è la condizione necessaria e sufficiente affinchè il punto P appartenga all'iperbole.
COSTRUZIONI
Le proprietà enunciate permettono le seguenti costruzioni:
1)-costruire per punti un'iperbole, dati gli asintoti ed un punto.
Siano r ed s gli asintoti e P un punto. Si conduce per P la retta generica m e siano C e D le intersezioni con gli asintoti. Per la prima proprietà enunciata, l'ulteriore intersezione Q di m con l'iperbole dev'essere tale che PD = CQ. Il punto Q si determina portando sulla retta CD, a partire dal punto C un segmento uguale a PD. Ripetendo la costruzione si trovano altri punti dell'iperbole. In figura sono indicate le costruzioni dei punti M e R.
2)-Costruire per tangenti un'iperbole, dati gli asintoti ed una tangente.
Siano r e s gli asintoti e t la tangente data; si indicano con M e N i punti di intersezione dalla tangente con gli asintoti.
Per la terza proprietà, per costruire altre tangenti all'iperbole, occorre costruire rette che formano con gli asintoti, nell'angolo completo in cui è contenuta la curva, triangoli equivalenti al triangolo MON. Poichè i triangoli devono avere un vertice in O, è sufficiente costruire rette che staccano sugli asintoti coppie di segmenti aventi prodotto uguale al prodotto dei segmenti staccati sugli asintoti dalla tangente data. Allo scopo, si riportano successivamente su una retta r i segmenti MO e ON, si costruisce la semicirconferenza di diametro MN e si conduce per O la perpendicolare alla r, che incontra la semicirconferenza in C. Per il teorema di Euclide, si ha:
Per costruire altre tangenti all'iperbole, si prende sulla retta r un punto P e si determina P', intersezione della perpendicolare in C alla retta PC con la r; si riporta sull'asintoto r, a partire da O, il segmento OP e sull'asintoto s il segmento OP'. La retta tangente PP' è una tangente all'iperbole. Infatti, si ha:
Facendo variare il punto P sulla retta r e con la costruzione suddetta, si determinano le tangenti all'iperbole nel numero desiderato.
Nota bene
Per la seconda proprietà è noto che il punto medio del segmento intercettato siulla tangente dagli asintoti è il punto di contatto, in modo che, determinando di ogni tangente il punto di contatto, può costruirsi l'iperbole luogo di punti.
3)-Data l'iperbole mediante gli asintoti r, s ed un punto P, costruire la tangente all'iperbole in P.
Si congiunge P con O e si porta su questa retta il segmento PM = OP, per M la parallela all'asintoto s fino ad incontrare in N l'asintoto r; la congiungente NP è la tangente richiesta.
Infatti, indicando con R l'intersezione di dalla t con l'asintoto s, i triangoli NMP e OPR sono uguali perchè hanno OP = PM per costruzione, gli angoli in P uguali, perchè opposti al vertice, l'angolo
,
perchè alterni interni, quindi PN = RP. Il punto P è,
dunque, il punto medio del segmento RN; segue che la retta RN è
la tangente all'iperbole nel punto P.4)-Costruire per tangenti un'iperbole di cui siano dati i fuochi F e F' ed il cerchio podaria.
Il cerchio podaria dell'iperbole è il cerchio di centro O avente come raggio il semiasse trasverso a. Per costruire la curva, si conducono dal fuoco F rette secanti il cerchio e dai punti di intersezioni le perpendicolari ad esse. Tali perpendicolari rappresentano tangenti all'iperbole. I punti di contatto delle tangenti sono dati dai punti medi dei segmenti staccati su di esse dagli asintoti. In figura è determinato il punto di contatto P della tangente t; esso è il punto medio del segmento MN. Gli asintoti, unica coppia di tangenti all'iperbole passanti per il centro, si ottengono congiungendo il centro del cerchio con i punti di contatto T e T' delle tangenti condotte da F al cerchio podaria.
