MIKY & GENNY
PARABOLA E COMPLEMENTI ---> INDICE
Definizione
- Si chiama parabola il luogo geometrico dei punti del piano equidistanti da un punto dato,
detto fuoco, e da una retta data, detta direttrice.
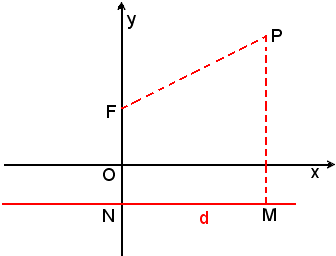
Un punto P del piano, per definizione, appartiene alla parabola di fuoco F e direttrice d, se e solo se soddisfa la relazione:
(1) PF = PM.
Per tradurre analiticamente la (1), si assume come asse y la perpendicolare per F alla direttrice d e come asse x la parallela alla d condotta per il punto medio O del segmento FN.
Se si indica con 1/2a la distanza FN, detta parametro della parabola, si ha:
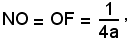
il fuoco F ha coordinate
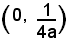
e la direttrice equazione
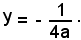
Indicando con x ed y le coordinate del punto P, la (1) diventa:
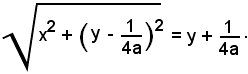
Elevando al quadrato:
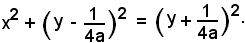
Semplificando ed ordinando si ottiene:
(2) y = ax2.
La (2) è definita equazione canonica della parabola; il numero
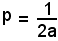
è definito parametro della parabola e rappresenta la distanza del fuoco dalla direttrice; la distanza
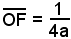
è definita distanza focale.
Scambiando il nome degli assi, la (2) diventa
x = ay2.
Tale equazione rappresenta la parabola di parametro
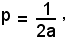
avente per fuoco il punto
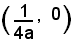
e per direttrice la retta
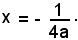
Proprietà della parabola
1)-Poichè nella (2) la variabile x si presenta di grado pari, la parabola è simmetrica rispetto all'asse y, il quale si chiama asse di simmetria della parabola.
2)-Le intersezioni della parabola con l'asse x sono date dalle soluzioni del sistema,
La parabola incontra l'asse x nell'origine delle coordinate, contato due volte; si deduce che l'asse x è tangente alla parabola nel punto O(0, 0).
3)-Le intersezioni della parabola con l'asse y sono date dalle soluzioni del sistema
La parabola incontra l'asse y nel punto O(0, 0), origine delle coordinate, il punto O si chiama vertice della parabola.
Si chiama vertice della parabola il punto d'intersezione della stessa con il suo asse.
Si osserva che quest'ultimo sistema, di secondo grado, ammette un'unica soluzione perchè l'equazione risolutiva y = 0 si abbassa di grado, ciò vuol dire che una delle soluzioni va all'infinito. Si dice quindi che:
-la parabola passa per il punto all'infinito dell'asse.
4)-Risolvendo l'equazione della parabola rispetto alla variabile x, si ha:
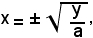
da cui si deduce come condizione di realtà
y > 0, se a > 0;
y < 0, se a < 0.
Si hanno dunque punti reali della curva solo nel semipiano che, limitato dall'asse x, contiene il semiasse positivo, se a > 0, o negativo, se a < 0, delle y.
Per a = 0, la parabola diventa degenere, coincidendo con l'asse delle x contato due volte.
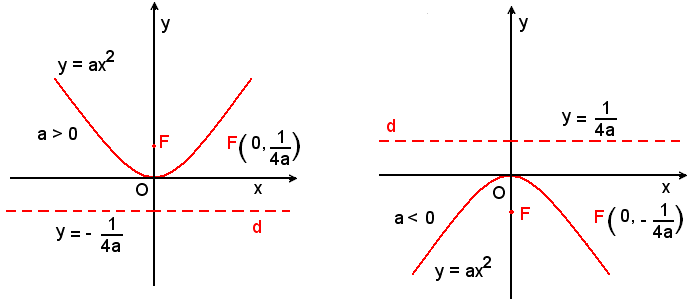
Retta tangente alla parabola in un suo punto
Si consideri la parabola di equazione y = ax2 e sia P(x0, y0) un suo punto; si vuole determinare l'equazione della retta tangente alla parabola nel punto P.
L'equazione di una retta generica uscente dal punto P(x0, y0) è:
y - y0 = m(x - x0).
Affinchè la retta sia tangente alla parabola in (x0, y0), è necessario che le due intersezioni retta-parabola coincidano in P. Le coordinate dei punti d'intersezione si trovano risolvendo il sistema:
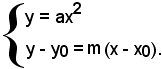
Sostituendo nella seconda equazione il valore di y, si ha:
(*) ax2 - mx + mx0 - y0 = 0.
Affinchè P appartenga alla parabola, è necessario che le sue coordinate soddisfino la sua equazione, cioè deve verificarsi:
Sostituendo tale valore in (*), si ottiene:
ax2 - mx + mx0 - ax02 = 0.
Tale equazione ha soluzioni coincidenti, se Δ = 0, cioè:
m2 - 4amx0 + 4a2x02 = 0,
ossia
(m - 2ax0)2 = 0,
da cui
m = 2ax0.
Sostituendo tale valore nella seconda equazione del sistema suddetto, si ha l'equazione della tangente alla parabola nel punto P(x0, y0); cioè:
y - y0 = 2ax0(x - x0)y0
ossia
y - y0 + 2ax02 = 2axx02;
ricordando che ax02 = y0, in quanto il punto P(x0, y0) appartiene alla parabola di equazione y = ax2, si ha:
y - y0 + 2y0 = 2axx02,
cioè
(3) y + y0 = 2axx02.
Se il punto P(x0, y0) non appartiene alla parabola (3) si definisce polare del punto P(x0, y0) rispetto alla parabola.
Si definisce polare di un punto rispetto alla parabola la retta congiungente i punti di contatto delle tangenti condotte dal punto alla parabola.
Se il punto P è esterno alla parabola, la polare è secante, se P è sulla polare, la polare è la tangente in P alla parabola, se P è interno, la polare è esterna, come si può notare anche dalla polarità rispetto alla circonferenza, ellisse, iperbole, ecc.
La (3) è l'equazione della tangente alla parabola nel punto P(x0, y0); essa si ottiene dall'equazione della parabola ponendo xx0 al posto di x2 e
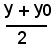
al posto di y, con operazione perfettamente analoga a quella per la tangente al cerchio, all'ellisse, ecc.
Tale formula si definisce di duplicazione o di sdoppiamento.
Esempio
Determinare l'equazione della tangente alla parabola y = x2 nel punto P(2, 4).
Primo procedimento
Una retta generica per P ha equazione
y - 4 = m(x - 2).
Tale retta è tangente alla parabola se le due intersezioni retta-parabola coincidono. Le coordinate dei punti d'intersezione retta-parabola sono date dalle soluzioni del sistema:
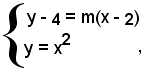
da cui, sostituendo il valore della y della prima equazione nella seconda,
x2 - mx + 2m - 4 = 0.
Le radici di tale equazione coincidono, se Δ = m2 - 8m + 16 = 0, cioè:
(m - 4)2 = 0
ossia
m = 4.
L'equazione della retta tangente alla parabola y = x2 nel punto P(1, 1) è:
y - 4 = 4(x - 2),
ossia
4x - y - 4 = 0.
Secondo procedimento
Applicando direttamente la formula di sdoppiamento, cioè sostituendo ad y il valore
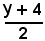
e ad x2 il valore 2x, si ha:
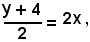
cioè
4x - y - 4 = 0.
Retta normale alla parabola in un suo punto
Si consideri la parabola di equazione y = ax2 e sia P(x0, y0) un suo punto; si vuole determinare l'equazione della retta normale alla parabola in P. L'equazione di una retta generica uscente dal punto P(x0, y0) è:
y - y0 = m(x - x0).
Affinchè tale retta sia normale alla parabola in P, occorre che il suo coefficiente angolare sia l'opposto e reciproco del coefficiente angolare della tangente alla parabola in P, cioè m dev'essere a -1/2ax0. L'equazione, dunque, della normale alla parabola y = ax2 nel punto P(x0, y0) è:
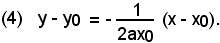
Si consideri l'equazione
(5) y = ax2 + bx + c, con a ≠ 0;
essa si può scrivere:
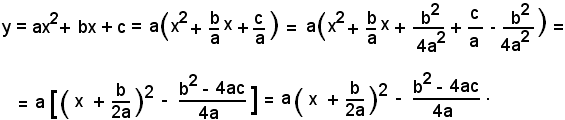
Posto
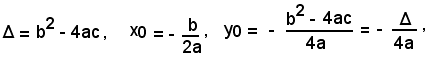
la (4) diventa:
y = a(x - x0)2 + y0,
ossia:
(6) y - y0 = (x - x0)2.
Traslando gli assi e portando l'origine nel punto V(x0, y0), si pone:
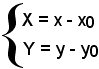
e l'equazione (6) diventa
per asse la retta, parallela all'asse y, di equazione x = -b/2a e per tangente nel vertice la retta y = -Δ/4a. Il parametro della (4) è ancora p = 1/2a. Il fuoco ha le coordinate
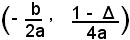
e la direttrice ha equazione
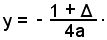Infatti, la parabola Y = aX2
ha il fuoco nel punto di coordinate (0, 1/4a) e direttrice la retta di
equazione Y = -1/4a; rispetto ai precedenti assi x ed y il punto (X =
0, Y = 1/4a) ha coordinate:
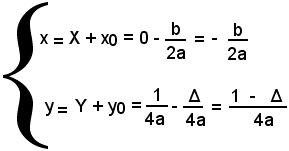
e la direttrice
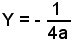
ha equazione
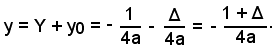
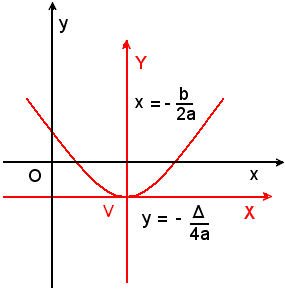
La parabola (5) è rivolta verso il semiasse positivo delle y, se a > 0; si dice anche che per a > 0 la curva ha la concavità rivolta verso l'alto.
Se a < 0 si dice che la curva ha la concavità rivolta verso il basso.
L'equazione x = ay2 + by + c rappresenta una parabola avente per asse la retta parallela all'asse x di equazione y = -b/2a, per vertice V' di coordinate x1 = -Δ/4a e y1 = -b/2a e per tangente nel vertice la retta di equazione x = -Δ/4a. Il parametro è ancora p = 1/2a.
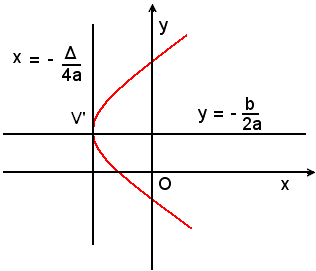
Il fuoco F ha coordinate
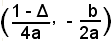
e la direttrice ha equazione
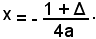
Esempi
1)-Calcolare le coordinate del vertice, del fuoco e scrivere le equazioni dell'asse e della direttrice della parabola di equazione:
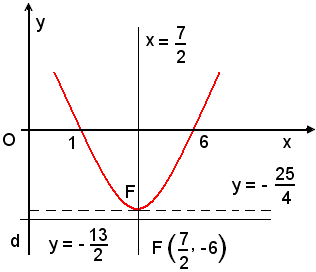
y = x2 - 7x + 6.
Le coordinate del vertice sono:
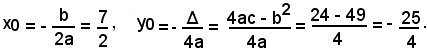
Le coordinate del fuoco sono:
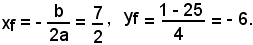
L'equazione dell'asse è
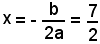
e quella della direttrice
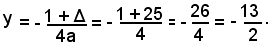
2)-Calcolare i coefficienti a, b, c in modo tale che la parabola di equazione y = ax2 + bx + c abbia il vertice nel punto di coordinate (2, 3) e che tagli l'asse y nel punto di coordinate (0, 2).
Affinchè la parabola passi per il punto (0, 2), la sua equazione dev'essere soddisfatta da x = 0 e y = 2, cioè deve aversi 2 = c.
Poichè le coordinate del vertice sono -b/2a e -Δ/4a, deve aversi:
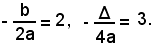
Risolvendo il sistema formato dalle tre relazioni trovate
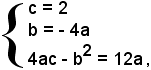
si ha:
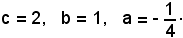
L'equazione della parabola richiesta è:
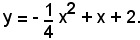
3)-Determinare l'equazione della parabola con l'asse parallelo all'asse x e passante per i punti (0, 0), (1, 3), (2, -3).
Affinchè una parabola passi per (0, 0), la sua equazione dev'essere soddisfatta per x = 0 e y = 0, pertanto si ha:
c =0.
Analogamente, per i punti (1, 3) e (2, -3), si ha rispettivamente:
1 = 9a + 3b + c,
2 = 9a - 3b + c.
Risolvendo il sistema, nelle incognite a, b, c, formato dalle tre relazioni trovate:
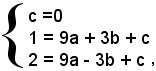
si ha
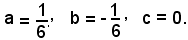
L'equazione della parabola richiesta è:
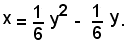
Intersezioni di una retta con una parabola
Le intersezioni di una retta con una parabola si determinano risolvendo il sistema formato lalle loro equazioni.
Se il sistema ha due soluzioni reali e distinte, la retta è secante; se ha due soluzioni reali e coincidenti, la retta è tangente; se non ammette soluzioni reali, la retta è esterna.
Esempi
1)-Determinare le intersezioni della retta y = x + 1 con la parabola y = x2 - 5x + 6.
Il sistema
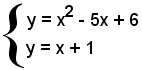
2)-Determinare le intersezioni della parabola y = x2 - 4x + 3 con la retta 4x + y - 3 = 0.
Il sistema
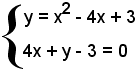
ammette due soluzioni coincidenti
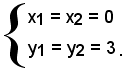La retta 4x + y - 3 = 0 è, dunque, tangente alla parabola nel punto (0, 3).
3)-Determinare le intersezioni della parabola y = x2 + x + 1 con la retta y = -5.
Il sistema
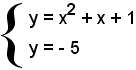La retta y = -5 è, dunque, esterna alla parabola.
4)-Determinare le intersezioni della parabola y = x2 - 4x + 3 con la retta x = 5. Le coordinate dei punti d'intersezione della parabola con la retta sono date dalle soluzioni del sistema
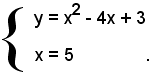
L'equazione risolvente del sistema è y = 8; poichè tale equazione si è abbassata di grado, in quanto il sistema è di secondo grado, una radice va all'infinito; cioè la retta x = 5 taglia la parabola nel punto proprio di coordinate (5, 8) e nel punto all'infinito dell'asse della parabola. Si può quindi affermare che:
-una retta parallela all'asse di una parabola ha con la curva un solo punto proprio d'intersezione.
5)-Determinare i coefficienti a, b, c in modo tale che la parabola di equazione y = ax2 + bx + c passi per il punto di coordinate (1, 4) e sia tangente alla retta x + y - 1 = 0 nel punto (3, 2). Un punto P del piano, per definizione, appartiene alla parabola di fuoco F e direttrice d, se e solo se soddisfa la relazione:
Per tradurre analiticamente la (1), si assume come asse y la perpendicolare per F alla direttrice d e come asse x la parallela alla d condotta per il punto medio O del segmento FN.
Se si indica con 1/2a la distanza FN, detta parametro della parabola, si ha:
il fuoco F ha coordinate
e la direttrice equazione
Indicando con x ed y le coordinate del punto P, la (1) diventa:
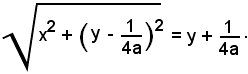
Elevando al quadrato:
Semplificando ed ordinando si ottiene:
(2) y = ax2.
La (2) è definita equazione canonica della parabola; il numero
è definito parametro della parabola e rappresenta la distanza del fuoco dalla direttrice; la distanza
è definita distanza focale.
Scambiando il nome degli assi, la (2) diventa
x = ay2.
Tale equazione rappresenta la parabola di parametro
avente per fuoco il punto
e per direttrice la retta
Proprietà della parabola
1)-Poichè nella (2) la variabile x si presenta di grado pari, la parabola è simmetrica rispetto all'asse y, il quale si chiama asse di simmetria della parabola.
2)-Le intersezioni della parabola con l'asse x sono date dalle soluzioni del sistema,
La parabola incontra l'asse x nell'origine delle coordinate, contato due volte; si deduce che l'asse x è tangente alla parabola nel punto O(0, 0).
3)-Le intersezioni della parabola con l'asse y sono date dalle soluzioni del sistema
La parabola incontra l'asse y nel punto O(0, 0), origine delle coordinate, il punto O si chiama vertice della parabola.
Si chiama vertice della parabola il punto d'intersezione della stessa con il suo asse.
Si osserva che quest'ultimo sistema, di secondo grado, ammette un'unica soluzione perchè l'equazione risolutiva y = 0 si abbassa di grado, ciò vuol dire che una delle soluzioni va all'infinito. Si dice quindi che:
-la parabola passa per il punto all'infinito dell'asse.
4)-Risolvendo l'equazione della parabola rispetto alla variabile x, si ha:
da cui si deduce come condizione di realtà
y > 0, se a > 0;
y < 0, se a < 0.
Si hanno dunque punti reali della curva solo nel semipiano che, limitato dall'asse x, contiene il semiasse positivo, se a > 0, o negativo, se a < 0, delle y.
Per a = 0, la parabola diventa degenere, coincidendo con l'asse delle x contato due volte.
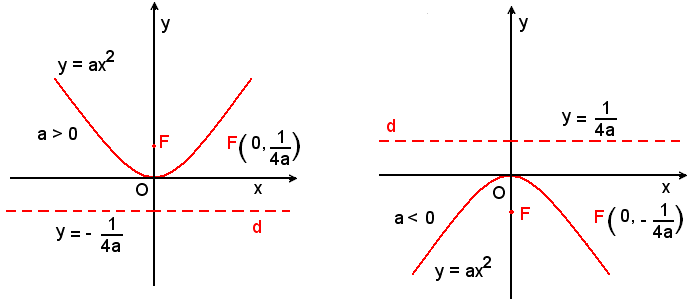
Retta tangente alla parabola in un suo punto
Si consideri la parabola di equazione y = ax2 e sia P(x0, y0) un suo punto; si vuole determinare l'equazione della retta tangente alla parabola nel punto P.
L'equazione di una retta generica uscente dal punto P(x0, y0) è:
y - y0 = m(x - x0).
Affinchè la retta sia tangente alla parabola in (x0, y0), è necessario che le due intersezioni retta-parabola coincidano in P. Le coordinate dei punti d'intersezione si trovano risolvendo il sistema:
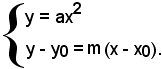
Sostituendo nella seconda equazione il valore di y, si ha:
(*) ax2 - mx + mx0 - y0 = 0.
Affinchè P appartenga alla parabola, è necessario che le sue coordinate soddisfino la sua equazione, cioè deve verificarsi:
y0 = ax02.
Sostituendo tale valore in (*), si ottiene:
ax2 - mx + mx0 - ax02 = 0.
Tale equazione ha soluzioni coincidenti, se Δ = 0, cioè:
m2 - 4amx0 + 4a2x02 = 0,
ossia
(m - 2ax0)2 = 0,
da cui
m = 2ax0.
Sostituendo tale valore nella seconda equazione del sistema suddetto, si ha l'equazione della tangente alla parabola nel punto P(x0, y0); cioè:
y - y0 = 2ax0(x - x0)y0
ossia
y - y0 + 2ax02 = 2axx02;
ricordando che ax02 = y0, in quanto il punto P(x0, y0) appartiene alla parabola di equazione y = ax2, si ha:
y - y0 + 2y0 = 2axx02,
cioè
(3) y + y0 = 2axx02.
Se il punto P(x0, y0) non appartiene alla parabola (3) si definisce polare del punto P(x0, y0) rispetto alla parabola.
Si definisce polare di un punto rispetto alla parabola la retta congiungente i punti di contatto delle tangenti condotte dal punto alla parabola.
Se il punto P è esterno alla parabola, la polare è secante, se P è sulla polare, la polare è la tangente in P alla parabola, se P è interno, la polare è esterna, come si può notare anche dalla polarità rispetto alla circonferenza, ellisse, iperbole, ecc.
La (3) è l'equazione della tangente alla parabola nel punto P(x0, y0); essa si ottiene dall'equazione della parabola ponendo xx0 al posto di x2 e
al posto di y, con operazione perfettamente analoga a quella per la tangente al cerchio, all'ellisse, ecc.
Tale formula si definisce di duplicazione o di sdoppiamento.
Esempio
Determinare l'equazione della tangente alla parabola y = x2 nel punto P(2, 4).
Primo procedimento
Una retta generica per P ha equazione
y - 4 = m(x - 2).
Tale retta è tangente alla parabola se le due intersezioni retta-parabola coincidono. Le coordinate dei punti d'intersezione retta-parabola sono date dalle soluzioni del sistema:
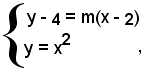
da cui, sostituendo il valore della y della prima equazione nella seconda,
x2 - mx + 2m - 4 = 0.
Le radici di tale equazione coincidono, se Δ = m2 - 8m + 16 = 0, cioè:
(m - 4)2 = 0
ossia
m = 4.
L'equazione della retta tangente alla parabola y = x2 nel punto P(1, 1) è:
y - 4 = 4(x - 2),
ossia
4x - y - 4 = 0.
Secondo procedimento
Applicando direttamente la formula di sdoppiamento, cioè sostituendo ad y il valore
e ad x2 il valore 2x, si ha:
cioè
4x - y - 4 = 0.
Retta normale alla parabola in un suo punto
Si consideri la parabola di equazione y = ax2 e sia P(x0, y0) un suo punto; si vuole determinare l'equazione della retta normale alla parabola in P. L'equazione di una retta generica uscente dal punto P(x0, y0) è:
y - y0 = m(x - x0).
Affinchè tale retta sia normale alla parabola in P, occorre che il suo coefficiente angolare sia l'opposto e reciproco del coefficiente angolare della tangente alla parabola in P, cioè m dev'essere a -1/2ax0. L'equazione, dunque, della normale alla parabola y = ax2 nel punto P(x0, y0) è:
Si consideri l'equazione
(5) y = ax2 + bx + c, con a ≠ 0;
essa si può scrivere:
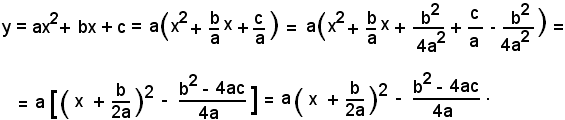
Posto
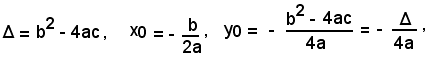
la (4) diventa:
y = a(x - x0)2 + y0,
ossia:
(6) y - y0 = (x - x0)2.
Traslando gli assi e portando l'origine nel punto V(x0, y0), si pone:
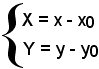
e l'equazione (6) diventa
Y = aX2,
che è l'equazione di una parabola.
Si ha dunque che l'equazione y = ax2 + bx + c rappresenta una parabola, avente il vertice nel punto V di coordinate
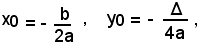
Si ha dunque che l'equazione y = ax2 + bx + c rappresenta una parabola, avente il vertice nel punto V di coordinate
per asse la retta, parallela all'asse y, di equazione x = -b/2a e per tangente nel vertice la retta y = -Δ/4a. Il parametro della (4) è ancora p = 1/2a. Il fuoco ha le coordinate
e la direttrice ha equazione
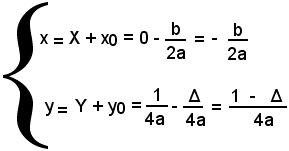
e la direttrice
ha equazione
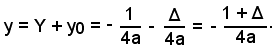
La parabola (5) è rivolta verso il semiasse positivo delle y, se a > 0; si dice anche che per a > 0 la curva ha la concavità rivolta verso l'alto.
Se a < 0 si dice che la curva ha la concavità rivolta verso il basso.
L'equazione x = ay2 + by + c rappresenta una parabola avente per asse la retta parallela all'asse x di equazione y = -b/2a, per vertice V' di coordinate x1 = -Δ/4a e y1 = -b/2a e per tangente nel vertice la retta di equazione x = -Δ/4a. Il parametro è ancora p = 1/2a.
Il fuoco F ha coordinate
e la direttrice ha equazione
Esempi
1)-Calcolare le coordinate del vertice, del fuoco e scrivere le equazioni dell'asse e della direttrice della parabola di equazione:
y = x2 - 7x + 6.
Le coordinate del vertice sono:
Le coordinate del fuoco sono:
L'equazione dell'asse è
e quella della direttrice
2)-Calcolare i coefficienti a, b, c in modo tale che la parabola di equazione y = ax2 + bx + c abbia il vertice nel punto di coordinate (2, 3) e che tagli l'asse y nel punto di coordinate (0, 2).
Affinchè la parabola passi per il punto (0, 2), la sua equazione dev'essere soddisfatta da x = 0 e y = 2, cioè deve aversi 2 = c.
Poichè le coordinate del vertice sono -b/2a e -Δ/4a, deve aversi:
Risolvendo il sistema formato dalle tre relazioni trovate
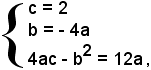
si ha:
L'equazione della parabola richiesta è:
3)-Determinare l'equazione della parabola con l'asse parallelo all'asse x e passante per i punti (0, 0), (1, 3), (2, -3).
Affinchè una parabola passi per (0, 0), la sua equazione dev'essere soddisfatta per x = 0 e y = 0, pertanto si ha:
c =0.
Analogamente, per i punti (1, 3) e (2, -3), si ha rispettivamente:
1 = 9a + 3b + c,
2 = 9a - 3b + c.
Risolvendo il sistema, nelle incognite a, b, c, formato dalle tre relazioni trovate:
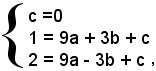
si ha
L'equazione della parabola richiesta è:
Intersezioni di una retta con una parabola
Le intersezioni di una retta con una parabola si determinano risolvendo il sistema formato lalle loro equazioni.
Se il sistema ha due soluzioni reali e distinte, la retta è secante; se ha due soluzioni reali e coincidenti, la retta è tangente; se non ammette soluzioni reali, la retta è esterna.
Esempi
1)-Determinare le intersezioni della retta y = x + 1 con la parabola y = x2 - 5x + 6.
Il sistema
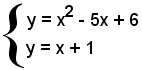
ammette le soluzioni
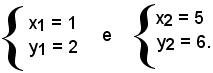
La retta y = x + 1 è secante la parabola nei punti A(1, 2) e B(5, 6).
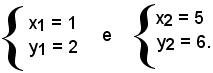
La retta y = x + 1 è secante la parabola nei punti A(1, 2) e B(5, 6).
2)-Determinare le intersezioni della parabola y = x2 - 4x + 3 con la retta 4x + y - 3 = 0.
Il sistema
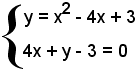
ammette due soluzioni coincidenti
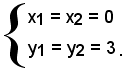
3)-Determinare le intersezioni della parabola y = x2 + x + 1 con la retta y = -5.
Il sistema
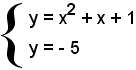
non ammette soluzioni reali.
4)-Determinare le intersezioni della parabola y = x2 - 4x + 3 con la retta x = 5. Le coordinate dei punti d'intersezione della parabola con la retta sono date dalle soluzioni del sistema
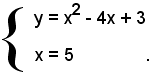
L'equazione risolvente del sistema è y = 8; poichè tale equazione si è abbassata di grado, in quanto il sistema è di secondo grado, una radice va all'infinito; cioè la retta x = 5 taglia la parabola nel punto proprio di coordinate (5, 8) e nel punto all'infinito dell'asse della parabola. Si può quindi affermare che:
-una retta parallela all'asse di una parabola ha con la curva un solo punto proprio d'intersezione.
Affinchè la parabola passi per il punto di coordinate (1, 4), la sua equazione dev'essere soddisfatta per x = 1 e y = 4, cioè deve aversi:
4 = a + b + c.
Inoltre, la parabola di equazione y = ax2 + bx + c è tangente alla retta x + y - 1 =0 nel punto (3, 2), se le radici dell'equazione ax2 + (b + 1)x + c -1 = 0, che fornisce le ascisse dei punti d'intersezione della retta con la parabola e che è risolutiva del sistema:
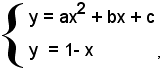
sono coincidenti ed uguali a 3.
L'equazione ax2 + (b + 1)x + c - 1 = 0 ha radici coincidenti ed uguali a 3, se e solo se il trinomio ax2 + (b + 1)x + c - 1 = 0 coincide con il trinomio ax2 - 6x + 9 = 0, e ciò si verifica se:
Risolvendo il sistema formato dalle tre relazioni trovate:
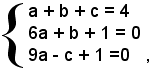
si ha:
a =1, b =- 7, c = 10.
L'equazione della parabola richiesta è:
y = x2 - 7x + 10.
L'equazione della parabola richiesta è:
y = x2 - 7x + 10.
Tangenti ad una parabola da un punto dato
1)-Determinare le tangenti alla parabola di equazione:
y = x2 - 5x + 6
uscenti dall'origine.
Una retta uscente da O(0, 0) ha equazione:
y = mx.
Affinchè tale retta sia tangente alla parabola, occorre che le due intersezioni della retta con la parabola coincidano.
Le coordinate dei punti d'intersezione si trovano risolvendo il sistema:
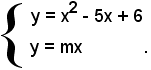
Sostituendo nella prima equazione del sistema il valore di y della seconda, si ha:
x2 - (5 + m)x + 6 = 0.
Tale equazione ha soluzioni coincidenti, se il suo discriminante è uguale a zero, cioè se:
(5 + m)2 - 24 = 0,
ossia
m2 + 10m + 1 = 0,
da cui
Le equazioni delle tangenti, condotte dall'origine alla parabola data, sono:
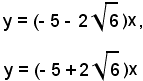
2)-Determinare le tangenti alla parabola di equazione:
y = x2 - 6x + 5
uscenti dal punto P(0, 5).
Una retta generica per P ha equazione:
y - 5 = mx.
Tale retta è tangente alla parabola, se l'equazione risolutiva del sistema formato dalle equazioni della retta e della parabola ammette due radici reali e coincidenti, cioè se l'equazione x2 - (6 + m)x = 0 ha il discriminante (6 + m)2 = 0, da cui m = -6.
Essendo dunque coincidenti i valori di m, le tangenti cercate coincidono, cioè il punto P appartiene alla parabola, e la tangente in esso ha equazione y - 5 = -6x, cioè 6x + y - 5 = 0.
COMPLEMENTI
Podaria del fuoco rispetto alla parabola
La podaria del fuoco rispetto alla parabola è il luogo dei piedi delle perpendicolari condotte dal fuoco alle tangenti alla parabola.
Si vuole dimostrare che la podaria del fuoco rispetto alla parabola è la tangente nel vertice.
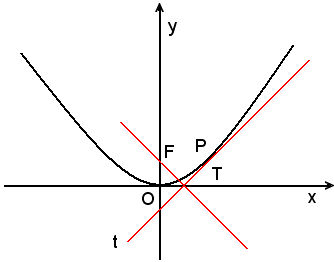
Allo scopo, si consideri la parabola di equazione y = ax2 e un suo punto P(x0, y0). La tangente in P ha equazione y + y0 = 2axx0; la retta uscente dal fuoco e perpendicolare alla tangente ha equazione:
Le coordinate del punto T, piede della perpendicolare condotta dal fuoco alla tangente, sono le soluzioni del sistema:
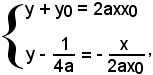
cioè
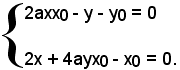
Moltiplicando la seconda equazione per ax0 e sottraendo membro a membro, si ha:
(4a2x02 + 1)y - ax02 + y0 = 0.
Ricordando che y0 = ax02, poichè P(x0, y0) sta sulla parabola, la precedente equazione diventa:
(4a2x02 + 1)y - ax02 + ax02 = 0,
cioè
(4a2x02 + 1)y = 0,
ossia
y = 0,
da cui si deduce che la podaria del fuoco rispetto alla parabola è l'asse x, y = 0, tangente nel vertice.
Tangente e normale alla parabola in un suo punto
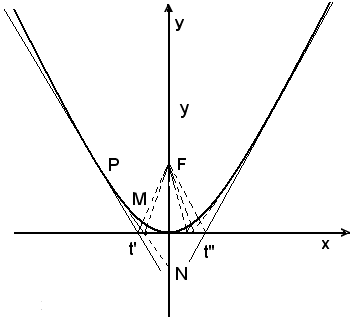
La tangente e la normale alla parabola in un suo punto sono le bisettrici degli angoli formati dalla retta che congiunge quel punto con il fuoco e dalla parallela all'asse per quel punto.
Sia γ la parabola, P un suo punto e t la retta tangente a γ in P.
Si vuole dimostrare che la retta t, tangente alla parabola in P, biseca l'angolo
, angolo formato dal raggio focale PF e dalla parallela per P all'asse della parabola.
Infatti, detta T l'intersezione di t con l'asse x, tangente nel vertice, si osservi che i triangoli FPT e TPM sono uguali perchè hanno PT in comune, i lati PF = PM, essendo P un punto della parabola, e gli angoli in T retti, essendo T un punto della podaria; di conseguenza l'angolo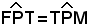
, ossia la retta t, è bisettrice dell'angolo .
Si osservi ancora come, nel triangolo isoscele FPM, la PT è non solo bisettrice, ma anche mediana, di modo che:
-il punto T è il punto medio del segmento FM.
Nota bene
Si ricordi che il punto simmetrico del fuoco rispetto alla tangente appartiene alla direttice.
Se si indica ora con N il punto d'intersezione della tangente t con l'asse della parabola, si dimostra che T è il punto medio del segmento PN.
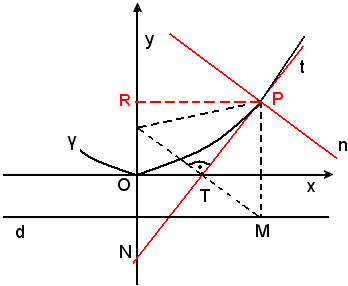
Infatti, il triangolo PFN, avendo gli angoli
uguali, perchè alterni interni rispetto alle parallele FN, PM intersecate dalla trasversale PN, bisettrice di , è isoscele. In esso FT, essendo altezza relativa alla base, è anche mediana, da cui PT = TN, cioè T è il punto medio del segmento PN.
Segue che i segmenti PT e TN hanno proiezioni uguali sull'asse x della parabola, ossia il punto N è il simmetrico, rispetto al vertice O, del punto R, proiezione di P sull'asse.
In conclusione:
-la tangente in un punto P di una parabola è la congiungente il punto P con il punto N, simmetrico, rispetto al vertice, della proiezione ortogonale di P sull'asse della parabola.
In base a tale proprietà si ha un procedimento rapido per scrivere l'equazione della tangente in un punto alla parabola; essa è la retta che congiunge i punti P e N.
Esempio
1)-Determinare l'equazione della tangente alla parabola y = ax2 nel punto P(1, 1).
Tale retta è la congiungente i punti P(1, 1) ed il punto N(0, -1), simmetrico rispetto all'origine del punto (0, 1), proiezione ortogonale di P sull'asse.
L'equazione della retta tangente è, dunque,
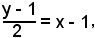
ossia
2x - y - 1 = 0.
In base alla proprietà enunciata sui può determinare il punto di contatto di una tangente alla parabola; è sufficiente condurre dal simmetrico, rispetto al vertice, del punto d'intersezione della tangente con l'asse della parabola la perpendicolare all'asse. Il punto d'intersezione di questa con la tangente dà il punto di contatto richiesto.
2)-Verificare che la tangente e la normale alla parabola y = ax2 nel punto P(3, 9) rappresentano le bisettrici dell'angolo formato dal raggio focale e dalla parallela per P all'asse. Verificare inoltre che il punto d'intersezione T di tale tangente con l'asse x, podaria, è il punto medio del segmento FM, ove M è l'intersezione della parallela all'asse per P, con la direttrice.
L'equazione della tangente alla parabola, come è noto, è:
6x - y - 9 = 0
e quella della normale
x + 6y - 57 = 0.
La parabola y = ax2 ha il fuoco nel punto F(0, 1/4); la retta PF ha equazione 35x - 12y + 3 = 0 e la parallela per P all'asse della parabola x = 3.
Le equazioni delle bisettrici dell'angolo formato dalle rette 35x - 12y + 3 = 0 e x - 3 = 0 sono:
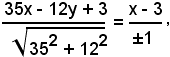
cioè
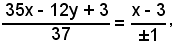
da cui
x + 6y - 57 = 0 e 6x - y - 9 = 0.
Le coordinate del punto d'intersezione della tangente 6x - y - 9 = 0 con l'asse x sono date dalla soluzione del sistema
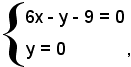
cioè T(3/2, 0); il punto medio del segmento avente per estremi F(0, 1/4) e M(3, -1/4) ha coordinate 3/2 e 0. Tale punto, dunque, coincide con il punto T.
COSTRUZIONI
1)-Costruire per punti la parabola, dati il fuoco F e la direttrice d.
Ricordando che y0 = ax02, poichè P(x0, y0) sta sulla parabola, la precedente equazione diventa:
(4a2x02 + 1)y - ax02 + ax02 = 0,
cioè
(4a2x02 + 1)y = 0,
ossia
y = 0,
da cui si deduce che la podaria del fuoco rispetto alla parabola è l'asse x, y = 0, tangente nel vertice.
Tangente e normale alla parabola in un suo punto
La tangente e la normale alla parabola in un suo punto sono le bisettrici degli angoli formati dalla retta che congiunge quel punto con il fuoco e dalla parallela all'asse per quel punto.
Sia γ la parabola, P un suo punto e t la retta tangente a γ in P.
Si vuole dimostrare che la retta t, tangente alla parabola in P, biseca l'angolo
, angolo formato dal raggio focale PF e dalla parallela per P all'asse della parabola.Infatti, detta T l'intersezione di t con l'asse x, tangente nel vertice, si osservi che i triangoli FPT e TPM sono uguali perchè hanno PT in comune, i lati PF = PM, essendo P un punto della parabola, e gli angoli in T retti, essendo T un punto della podaria; di conseguenza l'angolo
, ossia la retta t, è bisettrice dell'angolo .Si osservi ancora come, nel triangolo isoscele FPM, la PT è non solo bisettrice, ma anche mediana, di modo che:
-il punto T è il punto medio del segmento FM.
Nota bene
Si ricordi che il punto simmetrico del fuoco rispetto alla tangente appartiene alla direttice.
Se si indica ora con N il punto d'intersezione della tangente t con l'asse della parabola, si dimostra che T è il punto medio del segmento PN.
Infatti, il triangolo PFN, avendo gli angoli
uguali, perchè alterni interni rispetto alle parallele FN, PM intersecate dalla trasversale PN, bisettrice di , è isoscele. In esso FT, essendo altezza relativa alla base, è anche mediana, da cui PT = TN, cioè T è il punto medio del segmento PN.Segue che i segmenti PT e TN hanno proiezioni uguali sull'asse x della parabola, ossia il punto N è il simmetrico, rispetto al vertice O, del punto R, proiezione di P sull'asse.
In conclusione:
-la tangente in un punto P di una parabola è la congiungente il punto P con il punto N, simmetrico, rispetto al vertice, della proiezione ortogonale di P sull'asse della parabola.
In base a tale proprietà si ha un procedimento rapido per scrivere l'equazione della tangente in un punto alla parabola; essa è la retta che congiunge i punti P e N.
Esempio
1)-Determinare l'equazione della tangente alla parabola y = ax2 nel punto P(1, 1).
Tale retta è la congiungente i punti P(1, 1) ed il punto N(0, -1), simmetrico rispetto all'origine del punto (0, 1), proiezione ortogonale di P sull'asse.
L'equazione della retta tangente è, dunque,
ossia
2x - y - 1 = 0.
In base alla proprietà enunciata sui può determinare il punto di contatto di una tangente alla parabola; è sufficiente condurre dal simmetrico, rispetto al vertice, del punto d'intersezione della tangente con l'asse della parabola la perpendicolare all'asse. Il punto d'intersezione di questa con la tangente dà il punto di contatto richiesto.
2)-Verificare che la tangente e la normale alla parabola y = ax2 nel punto P(3, 9) rappresentano le bisettrici dell'angolo formato dal raggio focale e dalla parallela per P all'asse. Verificare inoltre che il punto d'intersezione T di tale tangente con l'asse x, podaria, è il punto medio del segmento FM, ove M è l'intersezione della parallela all'asse per P, con la direttrice.
L'equazione della tangente alla parabola, come è noto, è:
6x - y - 9 = 0
e quella della normale
x + 6y - 57 = 0.
La parabola y = ax2 ha il fuoco nel punto F(0, 1/4); la retta PF ha equazione 35x - 12y + 3 = 0 e la parallela per P all'asse della parabola x = 3.
Le equazioni delle bisettrici dell'angolo formato dalle rette 35x - 12y + 3 = 0 e x - 3 = 0 sono:
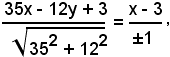
cioè
da cui
x + 6y - 57 = 0 e 6x - y - 9 = 0.
Le coordinate del punto d'intersezione della tangente 6x - y - 9 = 0 con l'asse x sono date dalla soluzione del sistema
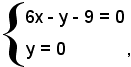
cioè T(3/2, 0); il punto medio del segmento avente per estremi F(0, 1/4) e M(3, -1/4) ha coordinate 3/2 e 0. Tale punto, dunque, coincide con il punto T.
COSTRUZIONI
1)-Costruire per punti la parabola, dati il fuoco F e la direttrice d.
Il rapporto delle distanze di un punto della parabola dal fuoco e dalla relativa direttrice si chiama eccentricità ed ha valore e = 1, mentre per l'ellisse e < 1 e per l'iperbole e > 1.
Quindi, per determinare i punti della curva, si descrive un cerchio, con centro F e raggio a piacere non minore di FO, e si conduce la parallela alla direttrice avente da questa distanza uguale al raggio del cerchio descritto e giacente dalla stessa banda di F rispetto alla direttice d. I punti d'intersezione M1 e M2 di tale retta con il cerchio sono punti della parabola.
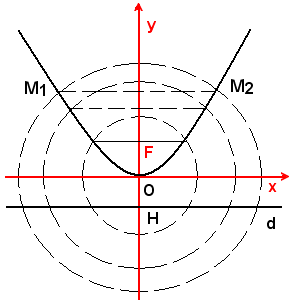
Descrivendo altri cerchi, con centro in F, e determinando i punti d'intersezione di questi con le corrispondenti rette parallele alla d ed aventi da questa distanze uguali ai raggi dei cerchi descritti, si hanno i punti desiderati della parabola.
Il vertice O della curva è dato dal punto medio del segmento FH, perpendicolare alla bisettrice condotto da F.
2)-Costruire la parabola per tangenti, dati il fuoco e la tangente nel vertice, podaria.
Sia F il fuoco e t la tangente nel vertice, podaria. La perpendicolare per F alla t è l'asse della parabola. Si conduce per il fuoco F una retta generica m, e sia M il punto in cui questa incontra la t; la perpendicolare in M alla FM è una tangente alla parabola.
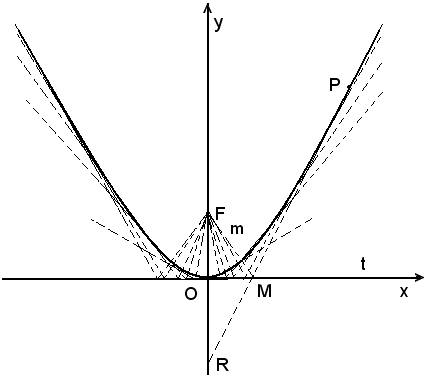
Per costruire il punto di contatto P della tangente, basta riportare sulla tangente il segmento MP uguale a MB; il punto P è il punto di contatto richiesto.
Variando la retta m, si ottengono tante tangenti alla parabola nel numero desiderato.
3)-Costruire la parabola, dati il fuoco F e due tangenti, t' e t''.
La podaria della parabola, luogo dei piedi delle perpendicolari condotte dal fuoco alle tangenti, è la tangente nel vertice. Da F si conducono le perpendicolari a t' e t''; la congiungente i punti d'intersezione è la tangente nel vertice della parabola. Si può costruire la parabola per tangenti, secondo la costruzione precedente.