MIKY & GENNY
TEOREMI DI GULDINO ---> INDICE
Baricentro
Siano P1 e P2 i centri di applicazione di due forze parallele, concordi e di uguale intensità.
Dalla fisica è noto che il punto di applicazione della risultante, dovendo dividere il segmento P1 P2 in due parti inversamente proporzionali alle loro intensità, è il punto medio M del segmento P1P2.
Questo punto è chiamato baricentro dei due punti dati.
La posizione del baricentro non cambia comunque si facciano ruotare le forze applicate P1 e P2 intorno ai rispettivi punti di applicazione, purchè permangano sempre parallele fra loro e comunque si alterino le loro intensità e rimangano nello stesso rapporto.
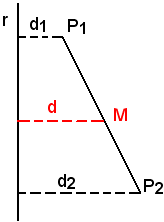
Si indicano ora con d1 e d2 le distanze di P1 e P2 da una retta r; la distanza d del baricentro M da r è data da:
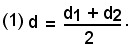
In generale, dati i punti P1, P2, P3, ..., Pn e indicate con d1, d2, d3, ..., dn, rispettivamente, le distanze di essi da una retta r, la distanza d del baricentro dai punti dati è uguale alla media aritmetica delle distanze ds, dove s = 1, 2, 3, ..., n, cioè:
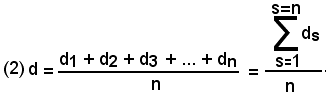
Se i punti Ps, con s = 1, 2, 3, ..., n, sono distribuiti lungo una linea e sufficientemente ravvicinati, si può, con una certa approssimazione, assumere come baricentro della linea il baricentro dei punti stessi.
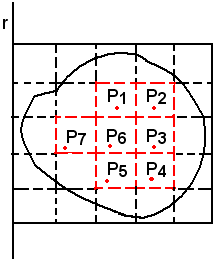
Se ora si racchiude una superficie piana in un quadrato, suddiviso in quadratini piccoli a piacere, e di essi si considerano solo quelli interni alla superficie, considerando di ognuno di essi si il proprio centro Ps (baricentro del quadratino), si può considerare come baricentro della superficie il baricentro dei punti Ps (centri).
Si ricorda che se una figura ha:
-un asse di simmetria, il baricentro appartiene ad esso;
-un centro di simmetria, il baricentro coincide con esso.
Esempio - Nei punti P1 e P2 sono concentrate masse uguali; determinare le coordinate del loro baricentro, sapendo che le coordinate dei punti sono P1(1, 2) e P2(3, -8).
Il baricentro M, punto medio del segmento P1P2, ha coordinate M(2, -3).
Area di una superficie di rotazione - Primo teorema di Guldino
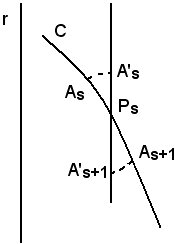
Si vuole determinare la superficie generata dalla rotazione completa di un arco AB di una curva C intorno ad un asse r che non l'attraversi.
Si divide l'arco in un numero n di archetti di uguale lunghezza e sufficientemente piccoli da poterli assimilare alle loro corde.
Sia
= h uno di questi archetti, l'area da esso descritta nella rotazione
completa intorno ad r è uguale a quella del cilindro descritto
dal segmento 
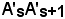, ottenuto facendo ruotare la corda 
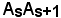intorno al baricentro Ps.
L'area S della superficie di rotazione è quindi, con una certa approssimazione, uguale alla somma delle aree dei cilindretti aventi uguale altezza h e come raggi le distanze ds dei punti As dall'asse.
Si ha, quindi:
S = 2π(d1 + d2 + d3, + ... + dn)h
e quindi, per la (2), se d è la distanza del baricentro della linea C dall'asse, risulta
S = 2πdnh;
posto nh = l, ed essendo l la lunghezza dell'arco della curva, si ha
(3) S = 2πdl.
La formula (3) esprime il primo teorema di Guldino:
-l'area della superficie di rotazione descritta da una linea piana finita, che ruota intorno ad un'asse del suo piano e che non l'attraversi, è uguale al prodotto della sua lunghezza per la lunghezza della circonferenza descritta dal baricentro dell'arco stesso.
Esempio - Determinare, applicando il primo teorema di Guldino la superficie del toro.
Il toro rappresenta il solido generato dalla rotazione completa di un cerchio intorno ad una retta del suo piano, la quale non l'attraversi.
La superficie S del toro generato dalla circonferenza di equazione:
(x - α)2 + (y - β)2 = r2
nella rotazione completa intorno all'asse y è data da
S = 2πr·2πα = 4π2rα,
ove α, distanza del cerchio dal suo centro all'asse y, è la distanza del baricentro del cerchio dall'asse di rotazione.
Volume di un solido di rotazione - Secondo teorema di Guldino
Si vuole determinare il volume del solido generato da una superficie piana di area S nella rotazione completa intorno ad un'asse che non l'attraversi.
Si scompone l'area S in quadratini aventi una coppia di lati paralleli all'asse di rotazione.
Con procedimento analogo a quello precedente, si ha:
(4) V = 2πdS,
essendo d la distanza del baricentro della superficie S dall'asse di rotazione.
La formula (4) esprime il secondo teorema di Guldino:
-il volume del solido generato da una superficie piana finita, nella rotazione completa intorno ad un'asse del suo piano e che non l'attraversi, è dato dal prodotto dell'area della superficie per la lunghezza della circonferenza descritta dal baricentro.
Esempio - Volume del toro, asse di rotazione asse y.
Volume del toro = Area del cerchio per la circonferenza descritta dal baricentro:
V = πR2·2πα = 4π2R2α.
Determinazione dei baricentri
I teoremi di Guldino, come si è visto, permettono di calcolare aree e volumi di rivoluzione, quando si conoscono i baricentri delle curve o delle sezioni meridiane; viceversa, si vuol far rilevare come i teoremi di Guldino servano a determinare anche i baricentri di una linea o superficie piana, quando si conosca l'area o il volume di rivoluzione da essi generato.
Esempio - Determinare, applicando il secondo teorema di Guldino, il baricentro di una semiellisse.
Siano a e b i semiassi dell'ellisse; si vuole determinare il baricentro della semiellisse limitata dall'asse minore. Per ragioni di simmetria, il baricentro deve trovarsi sull'altro asse.
Si fa ruotare la semiellisse intorno all'asse minore; si genera un'ellissoide rotondo di semiassi a, b, c=a, il cui volume è uguale a
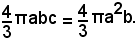
Si indica ora con d la distanza incognita di G dall'asse b e, applicando il secondo teorema di Guldino, si ha:
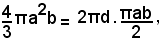
quindi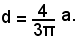
Siano P1 e P2 i centri di applicazione di due forze parallele, concordi e di uguale intensità.
Dalla fisica è noto che il punto di applicazione della risultante, dovendo dividere il segmento P1 P2 in due parti inversamente proporzionali alle loro intensità, è il punto medio M del segmento P1P2.
Questo punto è chiamato baricentro dei due punti dati.
La posizione del baricentro non cambia comunque si facciano ruotare le forze applicate P1 e P2 intorno ai rispettivi punti di applicazione, purchè permangano sempre parallele fra loro e comunque si alterino le loro intensità e rimangano nello stesso rapporto.
Si indicano ora con d1 e d2 le distanze di P1 e P2 da una retta r; la distanza d del baricentro M da r è data da:
In generale, dati i punti P1, P2, P3, ..., Pn e indicate con d1, d2, d3, ..., dn, rispettivamente, le distanze di essi da una retta r, la distanza d del baricentro dai punti dati è uguale alla media aritmetica delle distanze ds, dove s = 1, 2, 3, ..., n, cioè:
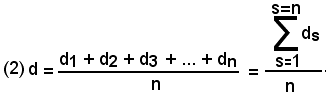
Se i punti Ps, con s = 1, 2, 3, ..., n, sono distribuiti lungo una linea e sufficientemente ravvicinati, si può, con una certa approssimazione, assumere come baricentro della linea il baricentro dei punti stessi.
Se ora si racchiude una superficie piana in un quadrato, suddiviso in quadratini piccoli a piacere, e di essi si considerano solo quelli interni alla superficie, considerando di ognuno di essi si il proprio centro Ps (baricentro del quadratino), si può considerare come baricentro della superficie il baricentro dei punti Ps (centri).
Si ricorda che se una figura ha:
-un asse di simmetria, il baricentro appartiene ad esso;
-un centro di simmetria, il baricentro coincide con esso.
Esempio - Nei punti P1 e P2 sono concentrate masse uguali; determinare le coordinate del loro baricentro, sapendo che le coordinate dei punti sono P1(1, 2) e P2(3, -8).
Il baricentro M, punto medio del segmento P1P2, ha coordinate M(2, -3).
Area di una superficie di rotazione - Primo teorema di Guldino
Si vuole determinare la superficie generata dalla rotazione completa di un arco AB di una curva C intorno ad un asse r che non l'attraversi.
Si divide l'arco in un numero n di archetti di uguale lunghezza e sufficientemente piccoli da poterli assimilare alle loro corde.
Sia
= h uno di questi archetti, l'area da esso descritta nella rotazione
completa intorno ad r è uguale a quella del cilindro descritto
dal segmento , ottenuto facendo ruotare la corda intorno al baricentro Ps.L'area S della superficie di rotazione è quindi, con una certa approssimazione, uguale alla somma delle aree dei cilindretti aventi uguale altezza h e come raggi le distanze ds dei punti As dall'asse.
Si ha, quindi:
S = 2π(d1 + d2 + d3, + ... + dn)h
e quindi, per la (2), se d è la distanza del baricentro della linea C dall'asse, risulta
S = 2πdnh;
posto nh = l, ed essendo l la lunghezza dell'arco della curva, si ha
La formula (3) esprime il primo teorema di Guldino:
-l'area della superficie di rotazione descritta da una linea piana finita, che ruota intorno ad un'asse del suo piano e che non l'attraversi, è uguale al prodotto della sua lunghezza per la lunghezza della circonferenza descritta dal baricentro dell'arco stesso.
Esempio - Determinare, applicando il primo teorema di Guldino la superficie del toro.
Il toro rappresenta il solido generato dalla rotazione completa di un cerchio intorno ad una retta del suo piano, la quale non l'attraversi.
La superficie S del toro generato dalla circonferenza di equazione:
(x - α)2 + (y - β)2 = r2
nella rotazione completa intorno all'asse y è data da
S = 2πr·2πα = 4π2rα,
ove α, distanza del cerchio dal suo centro all'asse y, è la distanza del baricentro del cerchio dall'asse di rotazione.
Volume di un solido di rotazione - Secondo teorema di Guldino
Si vuole determinare il volume del solido generato da una superficie piana di area S nella rotazione completa intorno ad un'asse che non l'attraversi.
Si scompone l'area S in quadratini aventi una coppia di lati paralleli all'asse di rotazione.
Con procedimento analogo a quello precedente, si ha:
(4) V = 2πdS,
essendo d la distanza del baricentro della superficie S dall'asse di rotazione.
La formula (4) esprime il secondo teorema di Guldino:
-il volume del solido generato da una superficie piana finita, nella rotazione completa intorno ad un'asse del suo piano e che non l'attraversi, è dato dal prodotto dell'area della superficie per la lunghezza della circonferenza descritta dal baricentro.
Esempio - Volume del toro, asse di rotazione asse y.
Volume del toro = Area del cerchio per la circonferenza descritta dal baricentro:
Determinazione dei baricentri
I teoremi di Guldino, come si è visto, permettono di calcolare aree e volumi di rivoluzione, quando si conoscono i baricentri delle curve o delle sezioni meridiane; viceversa, si vuol far rilevare come i teoremi di Guldino servano a determinare anche i baricentri di una linea o superficie piana, quando si conosca l'area o il volume di rivoluzione da essi generato.
Esempio - Determinare, applicando il secondo teorema di Guldino, il baricentro di una semiellisse.
Siano a e b i semiassi dell'ellisse; si vuole determinare il baricentro della semiellisse limitata dall'asse minore. Per ragioni di simmetria, il baricentro deve trovarsi sull'altro asse.
Si fa ruotare la semiellisse intorno all'asse minore; si genera un'ellissoide rotondo di semiassi a, b, c=a, il cui volume è uguale a
Si indica ora con d la distanza incognita di G dall'asse b e, applicando il secondo teorema di Guldino, si ha:
quindi