MIKY & GENNY
CIRCONFERENZA E CERCHIO ---> INDICE
CIRCONFERENZA
Generalità
Dato un segmento OA, si considera un punto fisso O intorno al quale si fa ruotare, in un certo senso, il segmento intorno ad O, di un giro completo. Il punto A descrive una linea chiusa, i cui punti godono della proprietà di avere la stessa distanza dal punto O. Tale linea prende il nome di circonferenza. Ogni altro punto del piano, che non appartiene alla circonferenza, ha distanza minore o maggiore di OA.
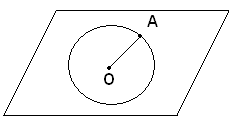
Lo strumento che si usa per tracciare una circonferenza è il compasso. Premesso ciò, si possono dare alcune definizioni.
Considerato un piano, si dice:
1)-circonferenza, il luogo dei punti equidistanti da un punto fisso.
2)-cerchio, l'insieme dei punti di un piano, che hanno da un punto dato distanza minore o uguale ad una distanza assegnata. Il punto equidistante dai punti della circonferenza si chiama centro; i segmenti che congiungono il centro con i singoli punti della circonferenza, si chiamano raggi. I raggi sono uguali per definizione. I punti che hanno dal centro distanza minore del raggio, sono interni alla circonferenza o al cerchio; quelli che hanno dal centro distanza maggiore del raggio, sono esterni alla circonferenza o al cerchio.
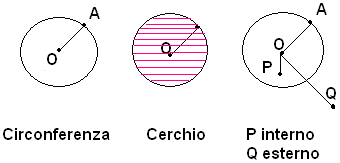
Il cerchio è una figura convessa, ossia se un segmento ha gli estremi appartenenti a un cerchio, tutti i suoi punti appartengono al cerchio.Si presentano tre casi:
1)-o gli estremi del segmento sono punti della circonferenza,
2)-o sono punti interni,
3)-o sono, uno sulla circonferenza e uno interno. In ogni caso, dopo aver congiunto gli estremi A e B del segmento dato, e uno dei suoi punti interni C col centro O del cerchio, si ottiene il triangolo OAB, nel quale il segmento OC è certamente minore di uno dei lati OA e OB del triangolo stesso. Ora, poichè questi lati sono o uguali o minori del raggio della circonferenza, si deduce che il segmento CO è minore del raggio e il punto C, avendo dal centro distanza minore del raggio, è interno al cerchio.
Una circonferenza o un cerchio si indicano col centro ed il raggio; quando non vi sia possibilità di equivoco, si indica solo il centro.
I punti di una circonferenza si possono ordinare in due versi associando ad ogni suo punto una semiretta di un angolo giro orientato, avente il vertice nel centro. Intuitivamente ciò corrisponde al fatto che una circonferenza può pensarsi descritta da un punto che ruoti nello stesso verso o nel verso contrario del movimento delle lancette dell'orologio.
Diametri e corde
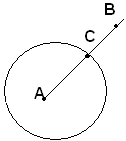
Si chiama corda ogni segmento che ha gli estremi sulla circonferenza.
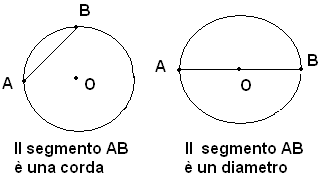
Ogni corda che passa per il centro si chiama diametro.Nelle figure suddette sono rappresentate la corda e il diametro della circonferenza.
Tutti i diametri di una stessa circonferenza sono uguali.
Infatti, ognuno di essi è la somma di due raggi.
Ogni diametro ha il suo punto medio nel centro del cerchio.
Da qui risulta che: un cerchio non può aver due centri, altrimenti ogni diametro avrebbe due punti medi.
Teorema: Il diametro di una circonferenza è maggiore di ogni altra corda, cioè il diametro è la corda massima.
Ipotesi: sia AB una corda qualsiasi, CD un diametro di un cerchio di centro O.
Tesi: si vuole dimostrare che il diiametro CD è maggiore della corda AB.
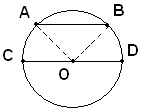
Dimostrazione
Infatti, si congiungono gli estremi A e B della corda con il centro O del cerchio e si ottiene il triangolo AOB, nel quale il lato AB è minore della somma degli altri due, OA e OB, cioè AB<OA+OB, ma OA e OB sono uguali ad OC e OD, in quanto raggi dello stesso cerchio, quindi AB<OC+OD, ed essendo OC+OD=CD, si ha AB<CD, ossia CD>AB, come volevasi dimostrare.
Teorema - Il diametro perpendicolare ad una corda la dimezza.
Viceversa: se un diametro dimezza una corda è perpendicolare ad essa.
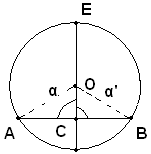
Ipotesi: sia data una circonferenza di centro O, avente diametro DE, perpendicolare nel punto C alla corda AB.
Tesi: si vuole dimostrare che AC=CB.Dimostrazione
Infatti, si considerano i triangoli AOC e COB; essi hanno uguali gli angoli α e α', retti per ipotesi, il lato OC in comune ed uguali i lati OA e OB, perchè raggi di uno stesso cerchio. Sono dunque uguali, perchè hanno l'ipotenusa e un cateto uguale e quindi segue che sono uguali anche i cateti AC e CB.
Viceversa
Ipotesi: siano uguali i segmenti AC e CB.
Tesi: si vuole dimostrare che il diametro DE è perpendicolare alla corda AB.
Dimostrazione
Infatti, i due triangoli ACO e OCB hanno il lato OC in comune, uguali i lati AO e OB come raggi dello stesso cerchio, ed uguali AC e CB per ipotesi, quindi per il terzo criterio di uguaglianza, sono uguali. Segue, in particolare, che i due angoli adiacenti α e α' sono uguali e quindi retti. Ciò dimostra che OC è perpendicolare ad AB.
Teorema - L'asse di una corda qualsiasi passa per il centro.
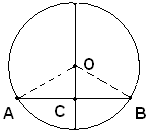
Ipotesi: siano dati il cerchio di centro O e una sua corda AB.
Tesi: si vuole dimostrare che l'asse di AB passa per il centro O del cerchio.
Dimostrazione
Infatti, essendo l'asse AB il luogo geometrico dei punti equidistanti da A e da B, contiene tutti i punti che godono di questa proprietà, perciò contiene anche il centro O equidistante per definizione, da tutti i punti della circonferenza.
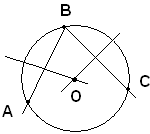
Corollario - Per tre punti non in linea retta passa una ed una sola circonferenza.
Ipotesi: siano dati tre punti non allineati A, B e C.
Tesi: si vuole dimostrare che per i punti A, B e C passa una ed una sola circonferenza.
Dimostrazione
Infatti, si considerano gli assi dei segmenti AB e BC e sia O il loro punto d'intersezione. Poichè O è comune agli assi delle corde AB e BC, è equidistante dai punti A, B e C. Pertanto, la circonferenza di centro O e raggio OB passa per A, B e C ed è unica, perchè se ne passasse un'altra dovrebbe avere lo stesso centro e lo stesso raggio, ossia coinciderebbe con se stessa.
Generalità
Dato un segmento OA, si considera un punto fisso O intorno al quale si fa ruotare, in un certo senso, il segmento intorno ad O, di un giro completo. Il punto A descrive una linea chiusa, i cui punti godono della proprietà di avere la stessa distanza dal punto O. Tale linea prende il nome di circonferenza. Ogni altro punto del piano, che non appartiene alla circonferenza, ha distanza minore o maggiore di OA.
Lo strumento che si usa per tracciare una circonferenza è il compasso. Premesso ciò, si possono dare alcune definizioni.
Considerato un piano, si dice:
1)-circonferenza, il luogo dei punti equidistanti da un punto fisso.
2)-cerchio, l'insieme dei punti di un piano, che hanno da un punto dato distanza minore o uguale ad una distanza assegnata. Il punto equidistante dai punti della circonferenza si chiama centro; i segmenti che congiungono il centro con i singoli punti della circonferenza, si chiamano raggi. I raggi sono uguali per definizione. I punti che hanno dal centro distanza minore del raggio, sono interni alla circonferenza o al cerchio; quelli che hanno dal centro distanza maggiore del raggio, sono esterni alla circonferenza o al cerchio.
Il cerchio è una figura convessa, ossia se un segmento ha gli estremi appartenenti a un cerchio, tutti i suoi punti appartengono al cerchio.
1)-o gli estremi del segmento sono punti della circonferenza,
2)-o sono punti interni,
3)-o sono, uno sulla circonferenza e uno interno. In ogni caso, dopo aver congiunto gli estremi A e B del segmento dato, e uno dei suoi punti interni C col centro O del cerchio, si ottiene il triangolo OAB, nel quale il segmento OC è certamente minore di uno dei lati OA e OB del triangolo stesso. Ora, poichè questi lati sono o uguali o minori del raggio della circonferenza, si deduce che il segmento CO è minore del raggio e il punto C, avendo dal centro distanza minore del raggio, è interno al cerchio.
Una circonferenza o un cerchio si indicano col centro ed il raggio; quando non vi sia possibilità di equivoco, si indica solo il centro.
I punti di una circonferenza si possono ordinare in due versi associando ad ogni suo punto una semiretta di un angolo giro orientato, avente il vertice nel centro. Intuitivamente ciò corrisponde al fatto che una circonferenza può pensarsi descritta da un punto che ruoti nello stesso verso o nel verso contrario del movimento delle lancette dell'orologio.
Diametri e corde
Si chiama corda ogni segmento che ha gli estremi sulla circonferenza.
Ogni corda che passa per il centro si chiama diametro.
Tutti i diametri di una stessa circonferenza sono uguali.
Infatti, ognuno di essi è la somma di due raggi.
Ogni diametro ha il suo punto medio nel centro del cerchio.
Da qui risulta che: un cerchio non può aver due centri, altrimenti ogni diametro avrebbe due punti medi.
Teorema: Il diametro di una circonferenza è maggiore di ogni altra corda, cioè il diametro è la corda massima.
Ipotesi: sia AB una corda qualsiasi, CD un diametro di un cerchio di centro O.
Tesi: si vuole dimostrare che il diiametro CD è maggiore della corda AB.
Dimostrazione
Infatti, si congiungono gli estremi A e B della corda con il centro O del cerchio e si ottiene il triangolo AOB, nel quale il lato AB è minore della somma degli altri due, OA e OB, cioè AB<OA+OB, ma OA e OB sono uguali ad OC e OD, in quanto raggi dello stesso cerchio, quindi AB<OC+OD, ed essendo OC+OD=CD, si ha AB<CD, ossia CD>AB, come volevasi dimostrare.
Teorema - Il diametro perpendicolare ad una corda la dimezza.
Viceversa: se un diametro dimezza una corda è perpendicolare ad essa.
Ipotesi: sia data una circonferenza di centro O, avente diametro DE, perpendicolare nel punto C alla corda AB.
Tesi: si vuole dimostrare che AC=CB.
Infatti, si considerano i triangoli AOC e COB; essi hanno uguali gli angoli α e α', retti per ipotesi, il lato OC in comune ed uguali i lati OA e OB, perchè raggi di uno stesso cerchio. Sono dunque uguali, perchè hanno l'ipotenusa e un cateto uguale e quindi segue che sono uguali anche i cateti AC e CB.
Viceversa
Ipotesi: siano uguali i segmenti AC e CB.
Tesi: si vuole dimostrare che il diametro DE è perpendicolare alla corda AB.
Dimostrazione
Infatti, i due triangoli ACO e OCB hanno il lato OC in comune, uguali i lati AO e OB come raggi dello stesso cerchio, ed uguali AC e CB per ipotesi, quindi per il terzo criterio di uguaglianza, sono uguali. Segue, in particolare, che i due angoli adiacenti α e α' sono uguali e quindi retti. Ciò dimostra che OC è perpendicolare ad AB.
Ipotesi: siano dati il cerchio di centro O e una sua corda AB.
Tesi: si vuole dimostrare che l'asse di AB passa per il centro O del cerchio.
Dimostrazione
Infatti, essendo l'asse AB il luogo geometrico dei punti equidistanti da A e da B, contiene tutti i punti che godono di questa proprietà, perciò contiene anche il centro O equidistante per definizione, da tutti i punti della circonferenza.
Corollario - Per tre punti non in linea retta passa una ed una sola circonferenza.
Ipotesi: siano dati tre punti non allineati A, B e C.
Tesi: si vuole dimostrare che per i punti A, B e C passa una ed una sola circonferenza.
Dimostrazione
Infatti, si considerano gli assi dei segmenti AB e BC e sia O il loro punto d'intersezione. Poichè O è comune agli assi delle corde AB e BC, è equidistante dai punti A, B e C. Pertanto, la circonferenza di centro O e raggio OB passa per A, B e C ed è unica, perchè se ne passasse un'altra dovrebbe avere lo stesso centro e lo stesso raggio, ossia coinciderebbe con se stessa.
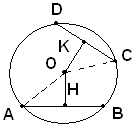
Teorema - In uno stesso cerchio, o in cerchi uguali, corde uguali hanno uguale distanza dal centro.
Viceversa, se due corde hanno uguale distanza dal centro, sono uguali.
Ipotesi: siano AB, CD due corde uguali della stessa circonferenza.
Tesi: si vuole dimostrare che le distanze OH e OK sono uguali.
Dimostrazione
Infatti, i due triangoli OHA e OKC
sono uguali, perchè hanno uguali le ipotenuse OA e OC, in quanto
raggi della circonferenza, ed uguali i cateti AH e CK, perchè
metà di corde uguali. Segue l'uguaglianza degli altri cateti,
cioè di OH e di OK.
Viceversa
Ipotesi: le distanze OH e OK di due corde AB e CD sono uguali.
Tesi: si vuole dimostrare che le corde AB e CD sono uguali.
Dimostrazione
Infatti, i due triangoli OHA e OKC sono uguali, perchè hanno uguali le ipotenuse OA, OC, in quanto raggi della circonferenza, ed uguali i cateti OH, OK per ipotesi. Sono pertanto uguali gli altri due cateti, cioè AH e CK, quindi anche le corde AB e CD, doppie di essi.
Archi e angoli al centro
Chiamasi arco una parte di circonferenza compresa fra due punti.
Per parte di una circonferenza compresa fra due punti bisogna intendere l'insieme dei punti che, in un verso fissato, seguono A e precedono B, o viceversa. I punti A e B si chiamano estremi dell'arco. Un arco di estremi A e B, si indica con
. Ogni corda che ha gli estremi in quelli di un arco si dice che sottende l'arco; si dice anche che l'arco sottende la corda. 
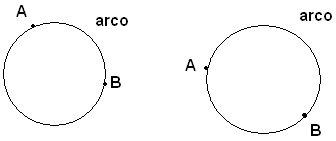
Archi consecutivi
Due archi
si dicono consecutivi se, in un determinato verso, B segue A e precede D.Angoli al centro
Dicesi angolo al centro di una circonferenza, un angolo che ha il vertice nel centro della stessa.
Angoli che insistono su un arco di circonferenza
Si dice che un angolo al centro insiste su un arco o corrisponde ad un arco, se l'arco è interno all'angolo ed ha gli estremi sui lati.
L'arco, a sua volta, si dice che corrisponde all'angolo al centro.
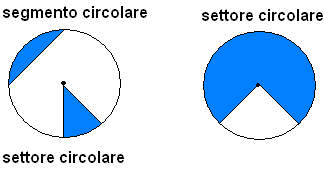
Settore
Per parte di cerchio compresa fra due raggi si deve intendere la parte interna al cerchio delimitata da un angolo al centro sui cui lati stanno i raggi. L'arco che limita il settore si dice base del settore
Segmento circolare
Si chiama segmento circolare una parte di cerchio compresa fra una corda e uno degli archi che la sottende.
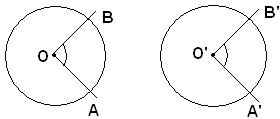
Teorema - In uno stesso cerchio, o in cerchi uguali, se due archi, o due settori sono uguali, tali sono gli angoli al centro corrispondenti.
Viceversa, se due angoli al centro sono uguali, sono anche uguali gli archi, o i settori, corrispondenti.
Ipotesi: in due cerchi di centri O, O' gli archi
sono uguali.Tesi: si vuole dimostrare che gli angoli al centro
corrispondenti ad essi, sono uguali.Dimostrazione
Viceversa
Ipotesi: sono uguali gli angoli al centro
in due cerchi uguali di centri O e O'.Tesi: si vuole dimostrare che sono uguali gli archi corrispondenti
e i settori corrispondenti.Dimostrazione
Infatti, si sovrappone l'angolo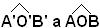 
in modo che la semiretta O'A' si sovrapponga ad OA e la semiretta O'B'
ad OB. Poichè i cerchi sono uguali, tali sono i loro raggi,
quindi i punti A e A', B e B' coincidono, e allo stesso modo gli archi
e i settoro corrispondenti ai due angoli.
in modo che la semiretta O'A' si sovrapponga ad OA e la semiretta O'B'
ad OB. Poichè i cerchi sono uguali, tali sono i loro raggi,
quindi i punti A e A', B e B' coincidono, e allo stesso modo gli archi
e i settoro corrispondenti ai due angoli.Corollario - Un diametro divide una circonferenza in due parti uguali chiamate semicirconferenze ed il cerchio in due parti uguali chiamate semicerchi.
Infatti, ognuna delle due parti in cui un diametro divide una circonferenza o un cerchio è un arco o un settore a cui corrisponde un angolo al centro piatto, e siccome gli angoli piatti sono uguali fra loro, anche gli archi e i settori corrispondenti sono rispettivamente uguali.
Teorema - In uno stesso cerchio, o in cerchi uguali, corde uguali sottendono archi uguali.
Viceversa, archi uguali sottendono corde uguali.
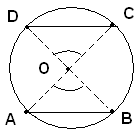
Ipotesi: siano AB e CD due corde uguali di uno stesso cerchio di centro O.
Tesi: si vuole dimostrare che gli archi
che sottendono le due corde sono uguali.Dimostrazione
Infatti,
i due triangoli AOB e COD sono uguali per il terzo criterio di
uguaglianza, in quanto hanno OA=OC e OB=OD, perchè raggi di uno
stesso cerchio, e AB=CD per ipotesi. Segue che gli angoli al centro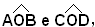 
opposti ai lati uguali AB e CD, sono uguali; quindi sono uguali gli archi 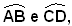corrispondenti agli angoli al centro uguali.
Viceversa
Infatti, gli angoli al centro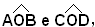 corrispondenti agli archi uguali 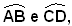sono uguali; pertanto i due
triangoli AOB e COD risultano uguali, perchè hanno uguali
rispettivamente due lati OA=OC, OB=OD, ed uguale l'angolo fra essi
compreso 
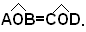Segue che AB=CD, cioè che sono uguali le corde sottese agli archi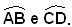 
Trasporto degli archi
In una circonferenza è possibile determinare un arco uguale ad un qualsiasi altro arco della stessa o di circonferenze uguali, partendo da un suo punto qualsiasi.
Infatti, dati un arco
e un punto C su una stessa circonferenza, per costruire CD=AB, basta prendere l'angolo al centro 
Somma di due archi consecutivi
La somma di due archi consecutivi è un arco che ha per estremi gli estremi non comuni.
Infatti, dati gli archi
Somma di due archi non consecutivi
La somma di due archi non consecutivi è uguale alla somma di due archi consecutivi uguali a quelli dati.
Infatti, dati gli archi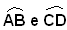
non consecutivi, se si considera 
si ha: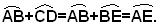 
Osservazione importante
Dopo aver definito la somma di due archi, in modo analogo a quanto fatto per i segmenti e per gli angoli, si definisce la somma di un numero qualsiasi di archi, la differenza di due archi, il multiplo e il sottomultiplo di un arco qualsiasi.
Quindi gli archi godono delle stesse proprietà degli angoli.
opposti ai lati uguali AB e CD, sono uguali; quindi sono uguali gli archi corrispondenti agli angoli al centro uguali.Viceversa
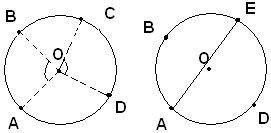
Ipotesi: gli archi 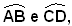della circonferenza di centro O sono uguali.
Tesi: si vuole dimostrare che le corde AB e CD sono uguali.
Dimostrazione della circonferenza di centro O sono uguali.Tesi: si vuole dimostrare che le corde AB e CD sono uguali.
Infatti, gli angoli al centro
corrispondenti agli archi uguali sono uguali; pertanto i due
triangoli AOB e COD risultano uguali, perchè hanno uguali
rispettivamente due lati OA=OC, OB=OD, ed uguale l'angolo fra essi
compreso Segue che AB=CD, cioè che sono uguali le corde sottese agli archi Trasporto degli archi
In una circonferenza è possibile determinare un arco uguale ad un qualsiasi altro arco della stessa o di circonferenze uguali, partendo da un suo punto qualsiasi.
Infatti, dati un arco
e un punto C su una stessa circonferenza, per costruire CD=AB, basta prendere l'angolo al centro Somma di due archi consecutivi
La somma di due archi consecutivi è un arco che ha per estremi gli estremi non comuni.
Infatti, dati gli archi
Somma di due archi non consecutivi
La somma di due archi non consecutivi è uguale alla somma di due archi consecutivi uguali a quelli dati.
Infatti, dati gli archi
non consecutivi, se si considera si ha: Osservazione importante
Dopo aver definito la somma di due archi, in modo analogo a quanto fatto per i segmenti e per gli angoli, si definisce la somma di un numero qualsiasi di archi, la differenza di due archi, il multiplo e il sottomultiplo di un arco qualsiasi.
Quindi gli archi godono delle stesse proprietà degli angoli.
Mutue posizioni di una retta e di una circonferenza
Postulato - Un segmento che congiunge un punto interno con un punto esterno di una circonferenza ha in comune con essa un solo punto.
La suddetta proposizione è stata ammessa come postulato perchè, anche se è evidente, non è possibile dimostrarla sulla scorta delle proprietà finora trattate.
Teorema - Data una retta e una circonferenza, se la distanza della retta dal centro della circonferenza è maggiore, minore, uguale del raggio, la retta ha nessuno, uno, due punti comuni con la stessa.
1)-La retta a ha distanza OH dal centro O della circonferenza maggiore del raggio OQ.
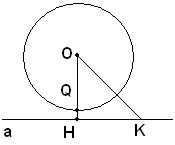
Poichè OH>OQ, il punto H è esterno alla circonferenza; e poichè per ogni altro punto K di a risulta OK>OH, a maggior ragione si ha OK>OQ e quindi OK è esterno al cerchio. Tutti i punti della retta a sono dunque esterni al cerchio.
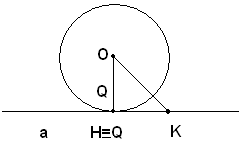
2)-Se OH=OQ, il punto H si trova sulla circonferenza, ma qualsiasi altro punto di a è esterno, perchè OK>OH e quindi OK>OQ. La circonferenza sta dalla stessa parte del suo centro rispetto ad una retta che ha un solo punto comune con essa.
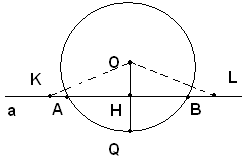
3)-Se OH<OQ, si considera una delle due semirette in cui H è l'origine e si prende un suo punto, per cui è HK=OQ. Nel triangolo rettangolo OHK risulta OK>HK, perchè l'ipotenusa è maggiore di un cateto; è dunque OK>OQ, perciò il punto K è esterno alla circonferenza. Per il postulato precedente, internamente al segmento HK esiste un punto A che sta sulla circonferenza. Analogamente, sull'altra semiretta esiste un altro punto B che sta sulla circonferenza. In conclusione, la retta a ha in comune con la circonferenza i due punti Ae B. Nessun altro punto di essa può essere comune con la circonferenza. Infatti, ogni altro punto o è interno alla corda AB, e quindi è interno al cerchio, o si trova sui prolungamenti, e allora ha distanza maggiore del raggio ed è perciò esterno.
Teorema - Data una retta e una circonferenza, se la retta ha nessuno, uno, due punti comuni con la circonferenza, la sua distanza dal centro è maggiore, uguale, minore del raggio della circonferenza.
Tale teorema si dimostra per esclusione.
Retta esterna, tangente e secante di una circonferenza
Una retta i cui punti sono tutti esterni ad una circonferenza dicesi esterna alla circonferenza; se ha un solo punto in comune dicesi tangente o di contatto e il punto comune si chiama punto di tangenza o di contatto; se ha due punti in comune si chiama secante.
Corollario - La perpendicolare ad un raggio di una circonferenza nella sua estremità, è tangente alla circonferenza. Viceversa, ogni tangente a una circonferenza è perpendicolare al raggio che ha un estremo nel punto di contatto.
Infatti, se una retta AB è perpendicolare al raggio OA nella sua estremità A, la sua distanza dal centro è uguale al raggio, quindi è tangente. Se viceversa una retta AB è tangente ad una circonferenza nel punto A, la sua distanza OA dal centro è uguale al raggio, e quindi è perpendicolare al raggio condotto per il punto di contatto.
Mutue posizioni di due circonferenze
Postulato
Un arco di circonferenza che congiunge due punti, uno interno e l'altro esterno, ad una data circonferenza, ha con questa un solo punto in comune.
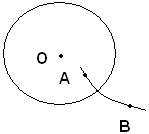
Teorema - Due circonferenze in un piano possono trovarsi in una delle seguenti posizioni:
1)-o sono mutuamente esterne;
2)-o una di esse è interna all'altra;
3)-o sono secanti;
4)-o sono tangenti esternamente;
5)-o sono tangenti internamente.
Nei primi due casi, non hanno nessun punto in comune, nel terzo ne hanno due, negli ultimi due casi ne hanno uno solo.
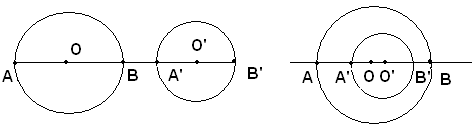
Se non hanno nessun punto in comune, per il postulato del cerchio, o una di esse è esterna all'altra, e sono naturalmente esterne per il primo caso, o una di esse è interna all'altra, per il secondo caso.
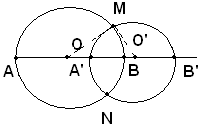
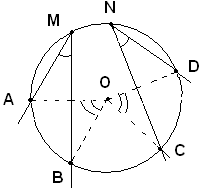
Se hanno in comune due punti M e M' questi devono essere fuori dalla retta OO' congiungente i centri, poichè il segmento MN è la corda di entrambe le circonferenze; viceversa si dimostra che se due circonferenze hanno un punto M in comune fuori dalla retta dei centri, hanno anche in comune un punto N, simmetrico di M rispetto alla retta congiungente i centri OO'; infatti, essendo OO' asse di MN, si ha: ON=OM e quindi N è anche sulla circonferenza di centro O'. Due circonferenze con due punti comuni si dicono secanti, terzo caso.
Se due circonferenze hanno un solo punto in comune, questo dev'essere sulla retta congiungente i centri O e O', altrimenti, se fosse esterno a tale retta, le due circonferenze, per il caso precedente, avrebbero due punti in comune e non uno solo.
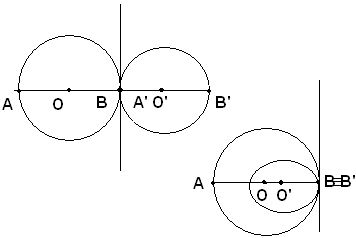
La perpendicolare condotta nel punto comune alla retta congiungente i centri, punto di contatto, è tangente ad entrambe le circonferenze e quindi lascia ciascuna dalla parte del proprio centro. Se le circonferenze sono da parti opposte rispetto alla tangente comune, si dicono tangenti esternamente, quarto caso; se le circonferenze sono dalla stessa parte, si dicono tangenti internamente, quinto caso.
Teorema - Date due circonferenze:
1)-se sono mutuamente esterne, la distanza dai centri è maggiore della somma dei raggi;
2)-se sono tangenti esternamente, la distanza dai centri è uguale alla somma dei raggi;
3)-se sono secanti, la distanza dai centri è minore della somma, ma maggiore della differenza dei raggi;
4)-se sono tangenti internamente, la distanza dei centri è uguale alla differenza dei raggi;
5)-se una circonferenza è interna all'altra, la distanza dei centri è minore della diffferenza dei raggi.
Siano date due circonferenza di centri O e O' e di raggi r e r', con r>r'. Si dimostrano separatamente le cinque parti del teorema.
Dimostrazione 1)
Le due circonferenze sono mutuamente esterne. I loro diametri AB e A'B' sono l'uno esterno all'altro.
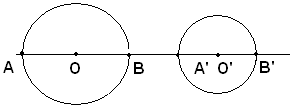
Si ha: OO'=OB+BA'+A'O', ossia d=r+BA'+r', da cui d>r+r'.
Dimostrazione 2)
Le due circonferenze sono tangenti esternamente.
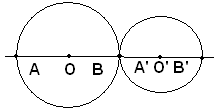
Poichè è OO'=OB+A'O', si ha: d=r+r'.
Dimostrazione 3)
Le circonferenze sono secanti, e sia M uno dei punti d'intersezione. Dal triangolo OO'M, poichè un lato dev'essere minore della somma degli altri due lati e maggiore della loro differenza, si ricava: OM-O'M'<OO'<OM+O'M, ossia: r-r'<d<r+r'.
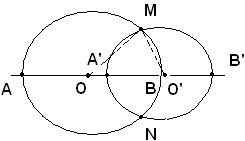
Dimostrazione 4)
Le due circonferenze sono tangenti internamente.
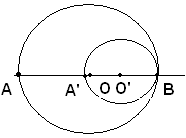
Si ha subito OO'=OB-O'B', ossia d=r-r'.
Dimostrazione 5)
La circonferenza O' di raggio minore è interna alla circonferenza di centro O. Se O' sta sul raggio OB, si ha: OO'+O'B'<OB, da cui, togliendo O'B' da ambo i membri, risulta OO'<OB-O'B', ossia d<r-r'.
Il teorema è quindi dimostrato in ogni caso.
Teorema - Date due circonferenza di raggi r e r', con r>r' i cui centri si trovano alla distanza d, esse sono rispettivamente esterne, tangenti esternamente, secanti, tangenti internamente, o l'una interna all'altra, a seconda che sono soddisfatte le seguenti relazioni: d>r+r'; d=r+r'; r-r'<d<r+r'; d=r-r'; d<r-r'.
Tale teorema si dimostra per esclusione.
Angoli alla circonferenza
Dicesi angolo alla circonferenza, un angolo che ha il vertice sulla circonferenza e i lati, o tutti e due secanti, oppure uno secante e l'altro tangente.
Si dice che un angolo alla circonferenza insiste su un dato arco della stessa circonferenza, o anche comprende quell'arco, se questo è interno all'angolo che ha gli estremi sui lati.
Così l'angolo alla circonferenza
che ha i lati entrambi secanti, insiste sull'arco 
l'angolo alla circonferenza 
con il lato DE secante il lato DF tangente, insiste sull'arco 
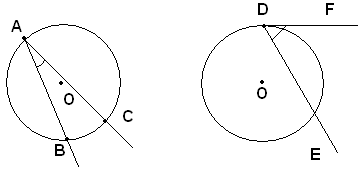
Un angolo che insiste su un arco di circonferenza si dice che è inscritto nell'arco rimanente.
Teorema - Un angolo alla circonferenza è metà dell'angolo al centro che insiste sullo stesso arco.
Dapprima si suppone che:
a)-i lati dell'angolo alla circonferenza siano entrambi secanti, distinguendo tre casi:
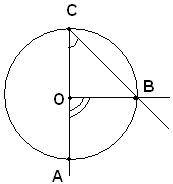
1)-uno dei lati dell'angolo alla circonferenza passa per il centro di essa.
Sia
l'angolo alla circonferenza di cui il lato CA passi per il centro O
della circonferenza e l'altro sia anche secante. Si dimostra che
l'angolo è metà dell'angolo al centro 
Infatti, essendo l'angolo
esterno al triangolo OCB, si ha: 
perchè il triangolo OCB è isoscele; è dunque:
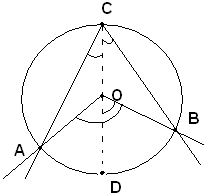
2)-Il centro del cerchio è interno all'angolo alla circonferenza.
Si traccia il diametro CD e si nota che gli angoli alla circonferenza
si trovano nelle condizioni del caso precedente e quindi risulta:
Sommando membro a membro, si ha:
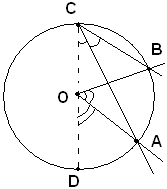
3)-Il centro O è esterno all'angolo alla circonferenza.
Si traccia il diametro CD e si nota che gli angoli alla circonferenza
si trovano nelle condizioni del primo caso e quindi risulta:
Sottraendo la seconda uguaglianza dalla prima, si ha:
b) - Resta da dimostrare che uno dei lati CB dell'angolo alla circonferenza
è tangente al cerchio.Si distinguono tre casi:
1)-il centro del cerchio sta sull'altro lato CA.
Se il centro O del cerchio si trova sul lato CA, l'angolo è piatto, mentre quello alla circonferenza è retto, e quindi metà dell'angolo al centro corrispondente.
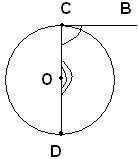
2)-Il centro del cerchio è interno all'angolo alla circonferenza.
Se il centro O del cerchio è interno all'angolo alla circonferenza
ed 
è l'angolo interno (concavo) che insiste sull'arco 
tracciando il diametro CD, si ha:
Sommando membro a membro, si ha:
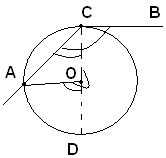
3)-Il centro del cerchio è esterno all'angolo alla circonferenza.
Se il centro O del cerchio è esterno all'angolo alla circonferenza
, ed è l'angolo al centro che insiste sullo stesso tracciando il diametro CD, si ha:Sottraendo la seconda uguaglianza dalla prima, si ha:
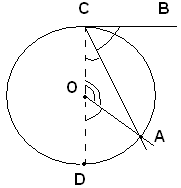
ll teorema è così dimostrato in ogni caso.
Corollario 1 - Angoli alla circonferenza che insistono su uno stesso arco, o su archi uguali, sono uguali.
Infatti, angoli alla circonferenza che insistono su uno stesso arco
sono tutti la metà dello stesso angolo al centro 
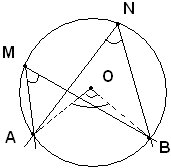
Se poi sull'arco
insiste l'angolo alla circonferenza 
e sull''arco 
l'angolo alla circonferenza 
ugual fra loro, sono uguali gli angoli al centro corrispondenti 
Di conseguenza, sono uguali gli angoli alla circonferenza dati, che sono la metà di questi angoli al centro.
Corollario 2 - Ogni angolo inscritto in una circonferenza è retto.
Infatti, se
è un angolo inscritto nella semicirconferenza 
esso insiste sull'altra semicirconferenza, e l'angolo al centro che insiste su questa è l'angolo piatto Quindi è la metà di un angolo piatto, cioè è un angolo retto.
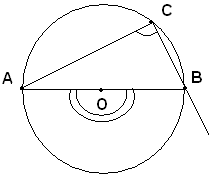
Un angolo si dice capace di un certo angolo α, se gli angoli inscritti in esso sono uguali all'angolo α.
Il corollario 2) si può enunciare così: una semicirconferenza è capace di un angolo retto.
Di vede facilmente che un arco maggiore di una semicirconferenza è capace di un angolo ottuso.
Teorema - Il luogo di punti dai quali un segmento è visto sotto un angolo dato, convesso, e che stanno da una stessa parte rispetto ad esso, è un arco capace dell'angolo dato e che ha per estremi gli estremi del segmento.
Ipotesi: dato il segmento AB ed un angolo α, si considera l'arco capace dell'angolo α che ha per estremi A e B e che sta da una parte prefissata rispetto ad AB.
Tesi: si vuole dimostrare che tale arco è il luogo dei punti dai quali il segmento AB è visto sotto l'angolo α.
Dimostrazione
Ogni altro punto al di fuori dell'arco
non gode di questa proprietà, cioè se un punto C è interno al segmento circolare 
Si
congiunge B con C e si prolunga fino ad incontrare l'arco in un punto
D, ed anche A con C e con D. Secondo il modo con cui il segmento AB si
vede da C, l'angolo è esterno rispetto al triangolo ACD, perciò è maggiore dell'angolo interno non adiacente, 
cioè è maggiore di α, essendo 
Se invece il punto E è al di fuori del segmento circolare 
il segmento AE incontra l'arco in un punto F e, per analoga ragione, l'angolo 
è maggiore dell'angolo di vertice E, cioè tale angolo è minore di α. Quindi, soltanto i punti dell'arco capace di α, hanno la proprietà di essere punti da cui il segmento AB si vede sotto l'angolo α.Osservazione
Se si considera tutto il piano, il luogo suddetto è formato da due archi che hanno per estremi quelli del segmento e sono capaci dell'angolo α.
