MIKY & GENNY
EQUIVALENZA DI PARALLELOGRAMMI E TRIANGOLI ---> INDICE
GENERALITA'
Una regione piana è una porzione di piano limitata da una linea chiusa.
Due regioni piane uguali possono essere sovrapposte in modo che il loro contorno coincida perfettamente con il contorno dell'altra. Per tale ragione, si dice comunemente che le due figure uguali hanno la stessa forma. Esse, oltre la forma, hanno un'altra cosa in comune, che nel linguaggio normale si dice che hanno uguale superficie od uguale estensione. Quindi, due regioni piane uguali hanno due proprietà comuni: la forma e la superficie. Queste uguaglianze di forma e di superficie, e ciò s'intuisce che esistono contemporaneamente in due regioni piane uguali, sono indipendenti. In altri termini, esistono delle regioni piane di forma completamente diversa, alle quali quali si attribuisce intuitivamente uguale superficie. Ad esempio, se si devono dipingere due pareti, una rettangolare e l'altra quadrata, può darsi che occorre la stessa quantità di vernice per dipingere l'una o l'altra. In tale caso, si dice che le due pareti, pur avendo forma diversa, hanno uguale superficie. Questa esperienza, ed altre analoghe fanno riconoscere nelle figure delle proprietà comuni che esse possono avere indipendentemente dalla loro forma. Tali proprietà si chiamano di estensione o di superficie. Per studiare tali proprietà, cioè per decidere se due regioni piane hanno o meno la stessa superficie da un punto di vista geometrico, si devono avere dei criteri ben precisi. Questi criteri si ricavano dai postulati, i quali a loro volta si ricavano direttamente dal concetto intuitivo di superfIcie. A tal punto, si premettono alcune definizioni.
Due figure si dicono equivalenti, se hanno uguale superficie.
Se A e B sono due figure equivalenti, si scrive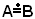 e si legge: A equivalente a B.
e si legge: A equivalente a B.
Somma di due figure
Date due figure A e B, che hanno in comune una parte del contorno, cioè sono adiacenti, e nessun'altro punto all'infuori di questo, cioè non ricoprentisi, si dice somma di A e di B la figura formata dall'insieme dei punti delle due figure.
Somma di più figure
La somma di più figure A, B, C,... a due a due adiacenti, ma non ricoprentisi, è la figura che si ottiene sommando A con B, la somma trovata con C, e così via. La somma di delle figure A, B, C, si indica con A+B+C.
Il contorno della somma di più figure è quello delle date, mancante di quella parte che le figure hanno in comune.
Somma di più figure non adiacenti
Per eseguire la somma di più figure non adiacenti, si sostituiscono ad esse altrettante figure rispettivamente uguali alle date e a due a due adiacenti. Bisogna notare che la somma di due fugure dà luogo a figure diverse, come forma, a seconda della porzione di contorno che, prima di eseguire la somma, si pone in comune. Così la somma di due triangoli H e K può essere un un rettangolo, o ancora un triangolo o una figura d'altro genere, Dunque, due figure ottenute sommando due o più figure, rispettivamente uguali, non sono in generale uguali, cioè sovrapponibili. Tuttavia si riconosce che esse hanno la stessa superficie.
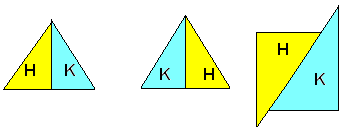
Figure prevalenti e suvvalenti
Se una figura A è equivalente alla somma di una figura B e di un'altra figura, la superficie di A si dice maggiore della superficie di B, ovvero A prevalente a B, e la superficie di B minore della superficie di A, ossia B suvvalente ad A e si scrive: A>B e B<A.
Differenza fra figure
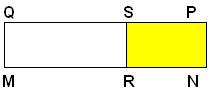
Se una figura A è somma di due figure B e C, la figura B si dice differenza di A e C, e si indica A-C. La figura C è la differenza, A-B, fra A e B.
Così la differenza fra il rettangolo MNPQ e il rettangolo MRSQ è il rettangolo RNPS.
Le proprietà fondamentali che, sotto forma di postulati, si mettono in evidenza affinchè il confronto fra due figure piane qualsiasi possono avere un significato preciso, scaturiscono immediatamente da quanto è stato detto per il concetto primitivo di superficie:
1)-due figure uguali sono equivalenti,
2)-per le figure equivalenti valgono le tre leggi delle uguaglianze:
a)-riflessiva: ogni figura è equivalente a se stessa,
b)-simmetrica: se una figura è equivalente ad un'altra, questa è equivalente alla prima,
c)-transitiva: due figure equivalenti ad una terza, sono equivalenti fra loro.
3)-Somme di figure equivalenti, sono equivalenti; In particolare, somme di figure uguali sono equivalenti.
In particolare, somme di figure uguali sono equivalenti.
4)-Date due figure uguali A e B qualsiasi, o sono equivalenti, o una delle due è prevalente all'altra, cioè si ha necessariamente: o A<b, o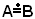 , o A<B.
, o A<B.
In base ai postulati precedenti si può dimostrare che valgono per l'equivalenza di due figure piane tutte le proprietà già ammesse per l'uguaglianza e la disuguaglianza, la somma, ecc., di segmenti. Così:
1)-se A è prevalente a B e B è prevalente a C, segue che A è prevalente a C.
2)-differenze di figure equivalenti sono equivalenti.
EQUIVALENZA DI PARALLELOGRAMMI E TRIANGOLI
Teorema - Due parallelogrammi aventi basi e altezze uguali sono equivalenti.
Ipotesi: siano ABCD, ABEF due parallelogrammi aventi la stessa base e la stessa altezza.
Tesi: si vuole dimostrare che i due parallelogrammi sono equivalenti.
Dimostrazione
Siccome i due parallelogrammi dati hanno uguale altezza, i due lati opposti ad AB, cioè CE e EF, risultanti dalla stessa parte rispetto alla base comune, si trovano su una retta parallela ad AB. Si distinguono tre casi:
1)-le basi CD e EF hanno una parte comune.
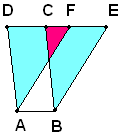
I due parallelogrammi ABCD e ABEF hanno il trapezio ABCF in comune, i triangoli DAF e CBE sono inoltre uguali, in quanto AD=DC, perchè lati opposti del parallelogrammo ABCD, DF=CE, come differenza fra i segmenti uguali DC e FE e lo stesso segmento FC e gli angoli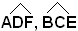 uguali perchè, corrispondenti fra le parallele AD e BC e la trasversale DE. Il parallelogrammo ABCD è somma del trapezio ABCF e del triangolo DAF; il secondo parallelogrammo ABEF è somma dello stesso trapezio e dello stesso triangolo uguale al primo. Quindi si deduce che i due parallelogrammi sono equivalenti.
uguali perchè, corrispondenti fra le parallele AD e BC e la trasversale DE. Il parallelogrammo ABCD è somma del trapezio ABCF e del triangolo DAF; il secondo parallelogrammo ABEF è somma dello stesso trapezio e dello stesso triangolo uguale al primo. Quindi si deduce che i due parallelogrammi sono equivalenti.
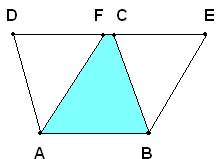
2)-Le basi CD e EF hanno un solo estremo in comune.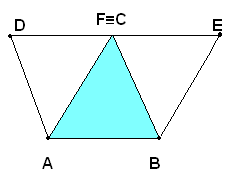
3)-Le basi CD E EF sono esterne l'una all'altra.
Si riporta sulla retta delle due basi, a partire da C e verso FE, un certo numero di segmenti consecutivi uguali a CD, fino ad ottenere un estremo M appartenente a FE, e ciò è possibile per il postulato di Archimede.
Se si congiungono A e B con gli estremi dei segmenti che si ottengono in tale modo, si ha una successione di parallelogrammi tali che il primo è equivalente al secondo, il secondo è equivalente al terzo e così via, in quanto due qualsiasi consecutivi si trovano nelle condizioni di uno dei due casi precedenti. Quindi, il primo, ABCD, e l'ultimo, ABEF, sono equivalenti.
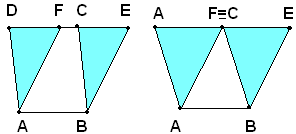
Altra dimostrazione: si pongono i due parallelogrammi in posizione tale che abbiano la base AB in comune e che giacciono da una stessa parte rispetto ad essa. Allora, i due lati opposti a tale base stanno su una retta parallela ad AB, in quanto i due parallelogrammi hanno la stessa altezza. I due lati opposti o coincidono, e in tal caso i parallelogrammi sono uguali, e quindi equivalenti; o hanno uno o più punti in comune, oppure non hanno alcun punto in comune. In ogni caso, riferendosi alle figure che seguono, i due triangoli DAF e CBE, sono uguali, perchè hanno AD=BC, in quanto lati opposti del parallelogrammo ABCD; AF=BE, in quanto lati opposti del parallelogrammo ABEF, ed uguali gli angoli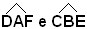 per avere i lati paralleli e concordi. Se si toglie
a tutto il trapezio ABED il triangolo CBE, si ottiene il parallelogrammo ABCD; se invece dallo stesso trapezio si toglie il triangolo DAF, si ottiene il parallelogrammo ABEF. Dunque, i due parallelogrammi
ABCD e ABEF sono equivalenti perchè differenza di poligoni
rispettivamente uguali. Da notare che dallo stesso trapezio sono stati
tolti triangoli uguali, una volta a destra e un'altra volta a sinistra.
per avere i lati paralleli e concordi. Se si toglie
a tutto il trapezio ABED il triangolo CBE, si ottiene il parallelogrammo ABCD; se invece dallo stesso trapezio si toglie il triangolo DAF, si ottiene il parallelogrammo ABEF. Dunque, i due parallelogrammi
ABCD e ABEF sono equivalenti perchè differenza di poligoni
rispettivamente uguali. Da notare che dallo stesso trapezio sono stati
tolti triangoli uguali, una volta a destra e un'altra volta a sinistra.
Teorema - Se due parallelogrammi sono equivalenti ed hanno altezze uguali, hanno uguali anche le basi corrispondenti.
Ipotesi: i due parallelogrammi ABCD e EFGH sono equivalenti ed hanno uguali le altezze relative alle basi AE e EF.
Tesi: si vuole dimostrare che le basi AB e EF sono uguali.
Dimostrazione
Infatti, si suppone che queste non sono uguali, e precisamente si considera EF>EB. Su EF si stacca un segmento EI=AB e da I si conduce la parallela a EH, fino ad incontrare HG in un punto L. Si ottiene quindi un terzo parallelogrammo EILH, il quale ha la stessa base e la stessa altezza di ABCD, quindi è a questo equivalente; ma poichè ABCD è equivalente per ipotesi ad EFGH, devono risultare equivalenti i due parallelogrammi EILH e EFGH. E questo è assurdo, perchè EFGH, essendo prevalente a EILH, non può essere ad esso equivalente. Resta così dimostrato che le basi AB ed EF dei due parallelogrammi sono uguali.
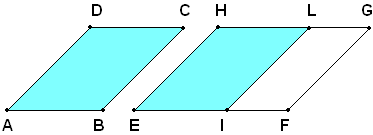
Analogamente, si dimostra che: se due parallelogrammi equivalenti hanno basi uguali, hanno anche uguali le altezze corrispondenti.
Teorema - Un triangolo è equivalente ad un parallelogrammo avente uguale altezza e base metà di quella del triangolo.
Ipotesi: sia ABC un triangolo e ADEC un parallelogrammo che ha la stessa altezza del triangolo e base metà di quella del triangolo.
Tesi: si vuole dimostrare che il triangolo ABC è equivalente al parallelogrammo ADEC.
Dimostrazione
Infatti, detta F l'intersezione di DE con il lato BC, i due triangoli CEF e BDF sono uguali, perchè , in quanto angoli alterni interni fra le parallele CE e DB e la trasversale BC;
, in quanto angoli alterni interni fra le parallele CE e DB e la trasversale BC;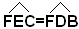 , in
quanto angoli alterni interni fra le stesse parallele e la trasversale
ED e i lati CE e DB uguali, perchè entrambi uguali ad AD. Ora, il
parallelogrammo è
equivalente alla somma del trapezio ADFC e del triangolo CEF; il
triangolo ABC è equivalente alla somma dello stesso trapezio e
del triangolo BDF, uguale al primo. Dunque, il triangolo ABC è il
parallelogrammo ADEC sono equivalenti in quanto somme di poligoni
uguali.
, in
quanto angoli alterni interni fra le stesse parallele e la trasversale
ED e i lati CE e DB uguali, perchè entrambi uguali ad AD. Ora, il
parallelogrammo è
equivalente alla somma del trapezio ADFC e del triangolo CEF; il
triangolo ABC è equivalente alla somma dello stesso trapezio e
del triangolo BDF, uguale al primo. Dunque, il triangolo ABC è il
parallelogrammo ADEC sono equivalenti in quanto somme di poligoni
uguali.
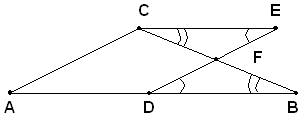
Teorema - Due triangoli aventi le basi uguali ed anche uguali le altezze ad esse relative sono equivalenti.
Ipotesi: i due triangoli ABC e A'B'C' hanno le basi AB e A'B' uguali e le altezze ad esse relative uguali.
Tesi: si vuole dimostrare che i due triangoli ABC e A'B'C' sono equivalenti.
Dimostrazione
Infatti, il triangolo ABC risulta equivalente al parallelogrammo ADEC avente la sua stessa altezza e metà base. Analogamente, il triangolo A'B'C' risulta equivalente al parallelogrammo A'D'E'C' avente la sua stessa altezza e metà base. Ma i due parallelogrammi ADEC e A'D'E'C' sono equivalenti perchè hanno la stessa altezza, cioè quella dei triangoli ABC e A'B'C', e la stessa base, che è la metà di quella degli stessi triangoli. Quindi anche i triangoli ABC e A'B'C' sono equivalenti fra loro.
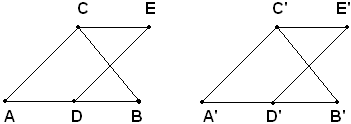
Corollario - Due o più triangoli aventi uguale base e i vertici opposti su una retta parallela a questa, sono equivalenti.
La dimostrazione è ovvia.
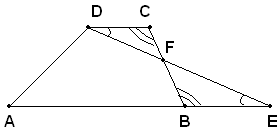
Teorema - Un trapezio è equivalente ad un triangolo avente uguale altezza e base uguale alla somma delle basi del trapezio.
Ipotesi: nel trapezio ABCD si prolunga il lato AB in E in modo che sia BE=DC e si congiunge D con E.
Tesi: si vuole dimostrare che il trapezio ABCD è equivalente al triangolo ADE.
Dimostrazione
Infatti, si indica con F l'intersezione di BC con AD; i triangoli DCF e EBF sono uguali perchè hanno DC=BE per costruzione, gli angoli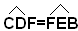 , perchè alterni interni fra le parallele DC e EB e la trasversale DE e
, perchè alterni interni fra le parallele DC e EB e la trasversale DE e 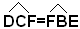 , perchè
alterni interni fra le stesse parallele e la trasversale CB. Ora, il
trapezio ABCD risulta formato dalla somma del quadrangolo ABFD e dal
triangolo EBF uguale a DCF. Quindi, il trapezio ABCD e il triangolo AED sono equivalenti.
, perchè
alterni interni fra le stesse parallele e la trasversale CB. Ora, il
trapezio ABCD risulta formato dalla somma del quadrangolo ABFD e dal
triangolo EBF uguale a DCF. Quindi, il trapezio ABCD e il triangolo AED sono equivalenti.
Teorema - Ogni poligono circoscritto ad una circonferenza è equivalente ad un triangolo avente per base il perimetro del poligono e per altezza il raggio della circonferenza inscritta.
Ipotesi: il triangolo A'O'A'' ha per base il perimetro del poligono ABCDE e per altezza il raggio della circonferenza inscritta.
Tesi: si vuole dimostrare che il poligono ABCDE è equivalente al triangolo A'O'A''.
Dimostrazione
Infatti, divisa la base A'A'' in parti rispettivamentre uguali ai lati del poligono, si congiunge O' con i punti di divisione B', C', D' e E': si ottengono triangoli che hanno le basi e le altezze rispettivamente uguali a quelle dei triangoli in cui viene scomposto il poligono dato congiungendo i vertici A, B, C, D e E, con il centro O della circonferenza inscritta.
Il poligono dato ed il triangolo A'O'A'' risultano quindi equivalenti, essendo somme di triangoli a due a due equivalenti.
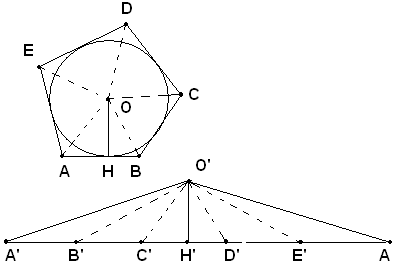
Corollario - un poligono regolare è equivalente ad un triangolo avente per base il perimetro e per altezza l'apotema.
Infatti, nel poligono regolare si può inscrivere una circonferenza che ha per raggio l'apotema.
Una regione piana è una porzione di piano limitata da una linea chiusa.
Due regioni piane uguali possono essere sovrapposte in modo che il loro contorno coincida perfettamente con il contorno dell'altra. Per tale ragione, si dice comunemente che le due figure uguali hanno la stessa forma. Esse, oltre la forma, hanno un'altra cosa in comune, che nel linguaggio normale si dice che hanno uguale superficie od uguale estensione. Quindi, due regioni piane uguali hanno due proprietà comuni: la forma e la superficie. Queste uguaglianze di forma e di superficie, e ciò s'intuisce che esistono contemporaneamente in due regioni piane uguali, sono indipendenti. In altri termini, esistono delle regioni piane di forma completamente diversa, alle quali quali si attribuisce intuitivamente uguale superficie. Ad esempio, se si devono dipingere due pareti, una rettangolare e l'altra quadrata, può darsi che occorre la stessa quantità di vernice per dipingere l'una o l'altra. In tale caso, si dice che le due pareti, pur avendo forma diversa, hanno uguale superficie. Questa esperienza, ed altre analoghe fanno riconoscere nelle figure delle proprietà comuni che esse possono avere indipendentemente dalla loro forma. Tali proprietà si chiamano di estensione o di superficie. Per studiare tali proprietà, cioè per decidere se due regioni piane hanno o meno la stessa superficie da un punto di vista geometrico, si devono avere dei criteri ben precisi. Questi criteri si ricavano dai postulati, i quali a loro volta si ricavano direttamente dal concetto intuitivo di superfIcie. A tal punto, si premettono alcune definizioni.
Due figure si dicono equivalenti, se hanno uguale superficie.
Se A e B sono due figure equivalenti, si scrive
Somma di due figure
Date due figure A e B, che hanno in comune una parte del contorno, cioè sono adiacenti, e nessun'altro punto all'infuori di questo, cioè non ricoprentisi, si dice somma di A e di B la figura formata dall'insieme dei punti delle due figure.
Somma di più figure
La somma di più figure A, B, C,... a due a due adiacenti, ma non ricoprentisi, è la figura che si ottiene sommando A con B, la somma trovata con C, e così via. La somma di delle figure A, B, C, si indica con A+B+C.
Il contorno della somma di più figure è quello delle date, mancante di quella parte che le figure hanno in comune.
Somma di più figure non adiacenti
Per eseguire la somma di più figure non adiacenti, si sostituiscono ad esse altrettante figure rispettivamente uguali alle date e a due a due adiacenti. Bisogna notare che la somma di due fugure dà luogo a figure diverse, come forma, a seconda della porzione di contorno che, prima di eseguire la somma, si pone in comune. Così la somma di due triangoli H e K può essere un un rettangolo, o ancora un triangolo o una figura d'altro genere, Dunque, due figure ottenute sommando due o più figure, rispettivamente uguali, non sono in generale uguali, cioè sovrapponibili. Tuttavia si riconosce che esse hanno la stessa superficie.

Figure prevalenti e suvvalenti
Se una figura A è equivalente alla somma di una figura B e di un'altra figura, la superficie di A si dice maggiore della superficie di B, ovvero A prevalente a B, e la superficie di B minore della superficie di A, ossia B suvvalente ad A e si scrive: A>B e B<A.
Differenza fra figure
Se una figura A è somma di due figure B e C, la figura B si dice differenza di A e C, e si indica A-C. La figura C è la differenza, A-B, fra A e B.
Così la differenza fra il rettangolo MNPQ e il rettangolo MRSQ è il rettangolo RNPS.

Le proprietà fondamentali che, sotto forma di postulati, si mettono in evidenza affinchè il confronto fra due figure piane qualsiasi possono avere un significato preciso, scaturiscono immediatamente da quanto è stato detto per il concetto primitivo di superficie:
1)-due figure uguali sono equivalenti,
2)-per le figure equivalenti valgono le tre leggi delle uguaglianze:
a)-riflessiva: ogni figura è equivalente a se stessa,
b)-simmetrica: se una figura è equivalente ad un'altra, questa è equivalente alla prima,
c)-transitiva: due figure equivalenti ad una terza, sono equivalenti fra loro.
3)-Somme di figure equivalenti, sono equivalenti;
4)-Date due figure uguali A e B qualsiasi, o sono equivalenti, o una delle due è prevalente all'altra, cioè si ha necessariamente: o A<b, o
In base ai postulati precedenti si può dimostrare che valgono per l'equivalenza di due figure piane tutte le proprietà già ammesse per l'uguaglianza e la disuguaglianza, la somma, ecc., di segmenti. Così:
1)-se A è prevalente a B e B è prevalente a C, segue che A è prevalente a C.
2)-differenze di figure equivalenti sono equivalenti.
EQUIVALENZA DI PARALLELOGRAMMI E TRIANGOLI
Teorema - Due parallelogrammi aventi basi e altezze uguali sono equivalenti.
Ipotesi: siano ABCD, ABEF due parallelogrammi aventi la stessa base e la stessa altezza.
Tesi: si vuole dimostrare che i due parallelogrammi sono equivalenti.
Dimostrazione
Siccome i due parallelogrammi dati hanno uguale altezza, i due lati opposti ad AB, cioè CE e EF, risultanti dalla stessa parte rispetto alla base comune, si trovano su una retta parallela ad AB. Si distinguono tre casi:
1)-le basi CD e EF hanno una parte comune.
I due parallelogrammi ABCD e ABEF hanno il trapezio ABCF in comune, i triangoli DAF e CBE sono inoltre uguali, in quanto AD=DC, perchè lati opposti del parallelogrammo ABCD, DF=CE, come differenza fra i segmenti uguali DC e FE e lo stesso segmento FC e gli angoli

2)-Le basi CD e EF hanno un solo estremo in comune.
La
dimostrazione è analoga a quella precedente, l'unica differenza
è che al posto del trapezio ABCF si considera il triangolo ABC.

3)-Le basi CD E EF sono esterne l'una all'altra.
Si riporta sulla retta delle due basi, a partire da C e verso FE, un certo numero di segmenti consecutivi uguali a CD, fino ad ottenere un estremo M appartenente a FE, e ciò è possibile per il postulato di Archimede.

Se si congiungono A e B con gli estremi dei segmenti che si ottengono in tale modo, si ha una successione di parallelogrammi tali che il primo è equivalente al secondo, il secondo è equivalente al terzo e così via, in quanto due qualsiasi consecutivi si trovano nelle condizioni di uno dei due casi precedenti. Quindi, il primo, ABCD, e l'ultimo, ABEF, sono equivalenti.
Altra dimostrazione: si pongono i due parallelogrammi in posizione tale che abbiano la base AB in comune e che giacciono da una stessa parte rispetto ad essa. Allora, i due lati opposti a tale base stanno su una retta parallela ad AB, in quanto i due parallelogrammi hanno la stessa altezza. I due lati opposti o coincidono, e in tal caso i parallelogrammi sono uguali, e quindi equivalenti; o hanno uno o più punti in comune, oppure non hanno alcun punto in comune. In ogni caso, riferendosi alle figure che seguono, i due triangoli DAF e CBE, sono uguali, perchè hanno AD=BC, in quanto lati opposti del parallelogrammo ABCD; AF=BE, in quanto lati opposti del parallelogrammo ABEF, ed uguali gli angoli


Teorema - Se due parallelogrammi sono equivalenti ed hanno altezze uguali, hanno uguali anche le basi corrispondenti.
Ipotesi: i due parallelogrammi ABCD e EFGH sono equivalenti ed hanno uguali le altezze relative alle basi AE e EF.
Tesi: si vuole dimostrare che le basi AB e EF sono uguali.
Dimostrazione
Infatti, si suppone che queste non sono uguali, e precisamente si considera EF>EB. Su EF si stacca un segmento EI=AB e da I si conduce la parallela a EH, fino ad incontrare HG in un punto L. Si ottiene quindi un terzo parallelogrammo EILH, il quale ha la stessa base e la stessa altezza di ABCD, quindi è a questo equivalente; ma poichè ABCD è equivalente per ipotesi ad EFGH, devono risultare equivalenti i due parallelogrammi EILH e EFGH. E questo è assurdo, perchè EFGH, essendo prevalente a EILH, non può essere ad esso equivalente. Resta così dimostrato che le basi AB ed EF dei due parallelogrammi sono uguali.

Analogamente, si dimostra che: se due parallelogrammi equivalenti hanno basi uguali, hanno anche uguali le altezze corrispondenti.
Teorema - Un triangolo è equivalente ad un parallelogrammo avente uguale altezza e base metà di quella del triangolo.
Ipotesi: sia ABC un triangolo e ADEC un parallelogrammo che ha la stessa altezza del triangolo e base metà di quella del triangolo.
Tesi: si vuole dimostrare che il triangolo ABC è equivalente al parallelogrammo ADEC.
Dimostrazione
Infatti, detta F l'intersezione di DE con il lato BC, i due triangoli CEF e BDF sono uguali, perchè

Teorema - Due triangoli aventi le basi uguali ed anche uguali le altezze ad esse relative sono equivalenti.
Ipotesi: i due triangoli ABC e A'B'C' hanno le basi AB e A'B' uguali e le altezze ad esse relative uguali.
Tesi: si vuole dimostrare che i due triangoli ABC e A'B'C' sono equivalenti.
Dimostrazione
Infatti, il triangolo ABC risulta equivalente al parallelogrammo ADEC avente la sua stessa altezza e metà base. Analogamente, il triangolo A'B'C' risulta equivalente al parallelogrammo A'D'E'C' avente la sua stessa altezza e metà base. Ma i due parallelogrammi ADEC e A'D'E'C' sono equivalenti perchè hanno la stessa altezza, cioè quella dei triangoli ABC e A'B'C', e la stessa base, che è la metà di quella degli stessi triangoli. Quindi anche i triangoli ABC e A'B'C' sono equivalenti fra loro.

Corollario - Due o più triangoli aventi uguale base e i vertici opposti su una retta parallela a questa, sono equivalenti.
La dimostrazione è ovvia.

Teorema - Un trapezio è equivalente ad un triangolo avente uguale altezza e base uguale alla somma delle basi del trapezio.
Ipotesi: nel trapezio ABCD si prolunga il lato AB in E in modo che sia BE=DC e si congiunge D con E.
Tesi: si vuole dimostrare che il trapezio ABCD è equivalente al triangolo ADE.
Dimostrazione
Infatti, si indica con F l'intersezione di BC con AD; i triangoli DCF e EBF sono uguali perchè hanno DC=BE per costruzione, gli angoli

Teorema - Ogni poligono circoscritto ad una circonferenza è equivalente ad un triangolo avente per base il perimetro del poligono e per altezza il raggio della circonferenza inscritta.
Ipotesi: il triangolo A'O'A'' ha per base il perimetro del poligono ABCDE e per altezza il raggio della circonferenza inscritta.
Tesi: si vuole dimostrare che il poligono ABCDE è equivalente al triangolo A'O'A''.
Dimostrazione
Infatti, divisa la base A'A'' in parti rispettivamentre uguali ai lati del poligono, si congiunge O' con i punti di divisione B', C', D' e E': si ottengono triangoli che hanno le basi e le altezze rispettivamente uguali a quelle dei triangoli in cui viene scomposto il poligono dato congiungendo i vertici A, B, C, D e E, con il centro O della circonferenza inscritta.
Il poligono dato ed il triangolo A'O'A'' risultano quindi equivalenti, essendo somme di triangoli a due a due equivalenti.

Corollario - un poligono regolare è equivalente ad un triangolo avente per base il perimetro e per altezza l'apotema.
Infatti, nel poligono regolare si può inscrivere una circonferenza che ha per raggio l'apotema.