MIKY & GENNY
LUOGHI GEOMETRICI ---> INDICE
DEFINIZIONE
Una figura è un luogo geometrico quando i suoi punti godono di una certa proprietà e sono i soli a goderla.
Da tale definizione si deduce che quando si deve dimostrare che una figura è un luogo geometrico di punti che godono di una certa proprietà, si deve verificare che:
1)-i punti della figura godono di quella proprietà;
2)-che viceversa ogni punto che gode di quella proprietà appartiene alla figura.
Esempi
1)-Il segmento è il luogo dei punti di una retta compresi fra due suoi punti dati A e B, in quanto qualsiasi punto del segmento è compreso fra i punti A e B, e viceversa qualsiasi punto compreso fra A e B appartiene al segmento.
2)-Il triangolo è il luogo geometrico di punti comuni ai suoi tre angoli, poichè qualsiasi punto del triangolo appartiene contemporaneamente ai suoi tre angoli, e viceversa qualsiasi punto appartenente ai tre angoli appartiene al triangolo.
Si ricorda ora che: che l'asse di un segmento è la retta perpendicolare al segmento nel suo punto medio.
Teorema - Il luogo dei punti equidistanti dagli estremi di un segmento è l'asse del segmento.
Ipotesi: sono assegnati il segmento AB e la perpendicolare r ad AB nel suo punto medio O.
Tesi: si deve dimostrare che r è il luogo geometrico dei punti equidistanti da A e da B, cioè che:
1)-ogni punto di r è equidistante da A e B,
2)-qualsiasi punto equidistante da A e da B si trova su r.
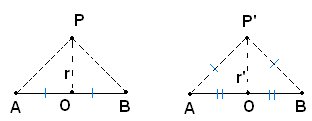
Dimostrazione
1)-Infatti, sia P un punto di r. I due triangoli rettangoli POA e POB sono uguali perchè hanno i cateti uguali, e precisamente PO in comune e OA=OB per ipotesi; di conseguenza PA=PB, cioè P è equidistante da A e da B.
2)-Se P' e un punto equidistante da A e da B, i triangoli P'AO e P'OB, avendo i lati uguali, sono uguali, e di conseguenza risultano uguali gli angoli in O con lati OP' e OA, e OP' e OB.
Siccome tali angoli sono adiacenti, essi sono retti. La retta OP' coincide con la perpendicolare in O ad AB, cioè con la retta r. Il punto P' perciò si trova su di essa.
Teorema - Il luogo dei punti equidistanti dai lati di un angolo è la bisettrice dell'angolo.
Ipotesi: siano α l'angolo dato e b la bisettrice.
Tesi: si vuole dimostrare che:
1)-i punti della bisettrice b sono equidistanti dai lati dell'angolo,
2)-un punto equidistante dai lati dell'angolo appartiene alla bisettrice b.
Dimostrazione
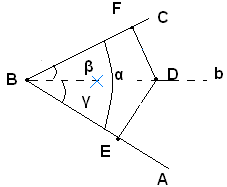
1)-Infatti, preso un punto D qualsiasi su b, si conducono le perpendicolari DE e DF ai due lati dell'angolo. I due triangoli rettangoli DBE e DBF risultano uguali per chè hanno l'ipotenusa DB in comune e gli angoli β e γ uguali per ipotesi. Si ha DE=DF e il punto D è perciò equidistante dai lati dell'angolo.
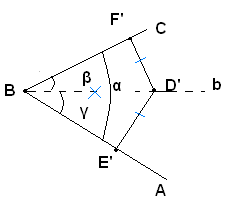
2)-Se D' è un punto tale che le distanze D'E' e D'F' dai lati dell'angolo risultino uguali, i triangoli rettangoli D'BE', D'BF', avendo due cateti uguali e l'ipotenusa in comune, sono uguali; perciò risulta β=γ. Ciò prova che D' appartiene alla bisettrice b, come dovevasi dimostrare.
PUNTI NOTEVOLI DI UN TRIANGOLO
Teorema - Gli assi dei tre lati di un triangolo concorrono in un punto equidistante dai vertici; tale punto si chiama circocentro.
Ipotesi: siano dati gli assi del triangolo ABC.
Tesi: Si vuole dimostrare che tali assi s'incontrano in un punto O equidistante dai vertici.
Dimostrazione
Infatti, per il teorema delle rette parallele "Se due rette s'incontrano, anche due rette ad esse rispettivamente perpendicolari s'incontrano", l'asse del lato AB e l'asse del lato BC s'incontrano in un punto O. Siccome O sta sull'asse AB, risulta OA=OB, quindi è OA=OB=OC, cioè il punto O è equidistante dai vertici del triangolo. Essendo in particolare OA=OC, O sta anche sull'asse AC.
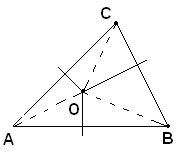
Osservazione - Il punto d'incontro degli assi dei lati è interno al triangolo, se il triangolo è acutangolo; è sull'ipotenusa se è rettangolo; è esterno se è ottusangolo.
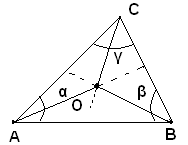
Teorema - Le bisettrici degli angoli di un triangolo concorrono in un punto equidistante dai lati; tale punto si chiama incentro.
Ipotesi: siano date le bisettrici degli angoli α, β e γ di un triangolo ABC.
Tesi: si vuole dimostrare che tali bisettrici s'incontrano in un punto O equidistante dai lati.
Dimostrazione
Infatti, le bisettrici degli angoli α e β s'incontrano certamente in un punto O. Ora, siccome il punto O sta sulla bisettrice dell'angolo α, esso è è ugualmente distante dai lati AB e AC, e siccome il punto O sta anche sulla bisettrice dell'angolo β, è ugualmente distante dai lati BA e BC. Dunque O è equidistante dai tre lati ndel triangolo. In particolare, essendo equidistante dai lati CA, CB, sta pure sulla bisettrice dell'angolo γ.
Teorema - Le altezze di un triangolo concorrono in un punto; tale punto si chiama ortocentro.
Ipotesi: sia dato il triangolo ABC.
Tesi: si vuole dimostrare che le tre altezze s'incontrano in un punto H.
Dimostrazione
Infatti, da ciascun vertice del triangolo si conduce la parallela al lato opposto ed in tal modo si forma il triangolo A'B'C'. Si dimostra ora che i vertici del triangolo dato sono i punti medi dei lati del nuovo triangolo. Se si esaminano i parallelogrammi ABCB' e ABA'C, risulta: nel primo CB'=AB e nel secondo AB=CA', pertanto è CB'=CA'. Quindi C è il punto medio del segmento A'B'. Allo stesso modo B e A risultano punti medi dei lati A'C' e C'B'. Inoltre, l'altezza condotta da C al lato AB, cioè l'altezza relativa ad AB, risulta perpendicolare anche ad A'B', poichè AB e A'B' sono parallele; segue che l'altezza relativa ad AB è asse di A'B'. Ad analoghe conclusioni si perviene per le altezze relative agli altri due lati del triangolo ABC. Quindi, le altezze del triangolo ABC sono gli assi dei lati del triangolo A'B'C', i quali concorrono in un punto.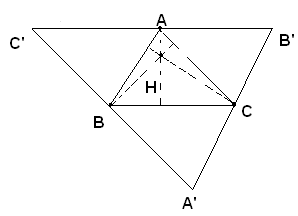
Osservazione - Nel triangolo acutangolo l'ortocentro è interno al triangolo; nel triangolo rettangolo coincide col vertice dell'angolo retto; nel triangolo ottusangolo è esterno.
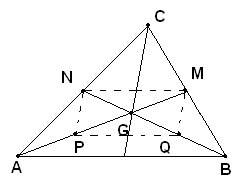
Teorema - Le mediane di un triangolo concorrono in un punto che divide ciascuna di esse in due parti delle quali quella che contiene il vertice è doppia dell'altra; tale punto si chiama baricentro.
Nel triangolo ABC si considerano le due mediane AM e BM e sia G il loro punto d'intersezione. Le due mediane s'incontrano sicuramente nel punto G, in quanto gli estremi di ciascuna di esse giacciono da parti opposte rispetto all'altra. Si considera il quadrilatero che ha per vertici M e N, ed i punti medi P e Q, rispettivamente di AG e BG e si dimostra che è un parallelogrammo. Infatti, i lati opposti MN e PQ, che congiungono i punti medi dei lati AC e BC e di AG e BG, essendo paralleli al lato AB e metà di questo, sono uguali fra loro e anche paralleli. Quindi risulta che MNPQ è un parallelogrammo. Segue che PG=GM, e poichè risulta AP=PG, i tre segmenti AP, PG e GM sono uguali fra loro. Ragionando allo stesso modo, risulta anche BQ=QG=GN. Perciò, le due mediane considerate s'incontrano in un punto G, il quale divide ciascuna di esse in due parti di cui una, quella che contiene il vertice, è doppia dell'altra. La terza mediana uscente da C, dovendo dividere ciascuna delle altre due alla stessa maniera, deve necessariamente passare per G, dal quale rimane essa stessa divisa in due parti come AM.
Il baricentro, l'ortocentro, l'incentro e il circocentro si dicono punti notevoli di un triangolo.
In un triangolo equilatero il baricentro, l'ortocentro, l'incentro e il circocentro coincidono in unico punto.
Infatti, in un triangolo equilatero la bisettrice, l'altezza e la mediana relativa ad un lato qualsiasi coincidono e con queste l'asse dello stesso lato.
Una figura è un luogo geometrico quando i suoi punti godono di una certa proprietà e sono i soli a goderla.
Da tale definizione si deduce che quando si deve dimostrare che una figura è un luogo geometrico di punti che godono di una certa proprietà, si deve verificare che:
1)-i punti della figura godono di quella proprietà;
2)-che viceversa ogni punto che gode di quella proprietà appartiene alla figura.
Esempi
1)-Il segmento è il luogo dei punti di una retta compresi fra due suoi punti dati A e B, in quanto qualsiasi punto del segmento è compreso fra i punti A e B, e viceversa qualsiasi punto compreso fra A e B appartiene al segmento.
2)-Il triangolo è il luogo geometrico di punti comuni ai suoi tre angoli, poichè qualsiasi punto del triangolo appartiene contemporaneamente ai suoi tre angoli, e viceversa qualsiasi punto appartenente ai tre angoli appartiene al triangolo.
Si ricorda ora che: che l'asse di un segmento è la retta perpendicolare al segmento nel suo punto medio.
Teorema - Il luogo dei punti equidistanti dagli estremi di un segmento è l'asse del segmento.
Ipotesi: sono assegnati il segmento AB e la perpendicolare r ad AB nel suo punto medio O.
Tesi: si deve dimostrare che r è il luogo geometrico dei punti equidistanti da A e da B, cioè che:
1)-ogni punto di r è equidistante da A e B,
2)-qualsiasi punto equidistante da A e da B si trova su r.

Dimostrazione
1)-Infatti, sia P un punto di r. I due triangoli rettangoli POA e POB sono uguali perchè hanno i cateti uguali, e precisamente PO in comune e OA=OB per ipotesi; di conseguenza PA=PB, cioè P è equidistante da A e da B.
2)-Se P' e un punto equidistante da A e da B, i triangoli P'AO e P'OB, avendo i lati uguali, sono uguali, e di conseguenza risultano uguali gli angoli in O con lati OP' e OA, e OP' e OB.
Siccome tali angoli sono adiacenti, essi sono retti. La retta OP' coincide con la perpendicolare in O ad AB, cioè con la retta r. Il punto P' perciò si trova su di essa.
Teorema - Il luogo dei punti equidistanti dai lati di un angolo è la bisettrice dell'angolo.
Ipotesi: siano α l'angolo dato e b la bisettrice.
Tesi: si vuole dimostrare che:
1)-i punti della bisettrice b sono equidistanti dai lati dell'angolo,
2)-un punto equidistante dai lati dell'angolo appartiene alla bisettrice b.
Dimostrazione
1)-Infatti, preso un punto D qualsiasi su b, si conducono le perpendicolari DE e DF ai due lati dell'angolo. I due triangoli rettangoli DBE e DBF risultano uguali per chè hanno l'ipotenusa DB in comune e gli angoli β e γ uguali per ipotesi. Si ha DE=DF e il punto D è perciò equidistante dai lati dell'angolo.
2)-Se D' è un punto tale che le distanze D'E' e D'F' dai lati dell'angolo risultino uguali, i triangoli rettangoli D'BE', D'BF', avendo due cateti uguali e l'ipotenusa in comune, sono uguali; perciò risulta β=γ. Ciò prova che D' appartiene alla bisettrice b, come dovevasi dimostrare.


Teorema - Il luogo dei punti aventi da una retta distanza
uguale ad un segmento assegnato è costituito da due rette
parallele alla data e aventi da questa distanza uguale al segmento
assegnato.
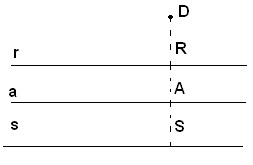
Siano
a la retta data, r ed s due rette giacenti ognuna in uno dei semipiani
aventi per origine a, parallele ad a e distanti da essa del segmento
assegnato h. Si sa già che i punti di r e di s sono
equidistanti da a. Viceversa, un punto D, non giacente su r o su
s, non può avere da a distanza h, poichè se fosse DA=h,
dovrebbe aversi DA=RA, cioè un segmento dovrebbe essere
uguale ad una parte, il che è assurdo.

PUNTI NOTEVOLI DI UN TRIANGOLO
Teorema - Gli assi dei tre lati di un triangolo concorrono in un punto equidistante dai vertici; tale punto si chiama circocentro.
Ipotesi: siano dati gli assi del triangolo ABC.
Tesi: Si vuole dimostrare che tali assi s'incontrano in un punto O equidistante dai vertici.
Dimostrazione
Infatti, per il teorema delle rette parallele "Se due rette s'incontrano, anche due rette ad esse rispettivamente perpendicolari s'incontrano", l'asse del lato AB e l'asse del lato BC s'incontrano in un punto O. Siccome O sta sull'asse AB, risulta OA=OB, quindi è OA=OB=OC, cioè il punto O è equidistante dai vertici del triangolo. Essendo in particolare OA=OC, O sta anche sull'asse AC.

Osservazione - Il punto d'incontro degli assi dei lati è interno al triangolo, se il triangolo è acutangolo; è sull'ipotenusa se è rettangolo; è esterno se è ottusangolo.
Teorema - Le bisettrici degli angoli di un triangolo concorrono in un punto equidistante dai lati; tale punto si chiama incentro.
Ipotesi: siano date le bisettrici degli angoli α, β e γ di un triangolo ABC.
Tesi: si vuole dimostrare che tali bisettrici s'incontrano in un punto O equidistante dai lati.
Dimostrazione
Infatti, le bisettrici degli angoli α e β s'incontrano certamente in un punto O. Ora, siccome il punto O sta sulla bisettrice dell'angolo α, esso è è ugualmente distante dai lati AB e AC, e siccome il punto O sta anche sulla bisettrice dell'angolo β, è ugualmente distante dai lati BA e BC. Dunque O è equidistante dai tre lati ndel triangolo. In particolare, essendo equidistante dai lati CA, CB, sta pure sulla bisettrice dell'angolo γ.

Teorema - Le altezze di un triangolo concorrono in un punto; tale punto si chiama ortocentro.
Ipotesi: sia dato il triangolo ABC.
Tesi: si vuole dimostrare che le tre altezze s'incontrano in un punto H.
Dimostrazione
Infatti, da ciascun vertice del triangolo si conduce la parallela al lato opposto ed in tal modo si forma il triangolo A'B'C'. Si dimostra ora che i vertici del triangolo dato sono i punti medi dei lati del nuovo triangolo. Se si esaminano i parallelogrammi ABCB' e ABA'C, risulta: nel primo CB'=AB e nel secondo AB=CA', pertanto è CB'=CA'. Quindi C è il punto medio del segmento A'B'. Allo stesso modo B e A risultano punti medi dei lati A'C' e C'B'. Inoltre, l'altezza condotta da C al lato AB, cioè l'altezza relativa ad AB, risulta perpendicolare anche ad A'B', poichè AB e A'B' sono parallele; segue che l'altezza relativa ad AB è asse di A'B'. Ad analoghe conclusioni si perviene per le altezze relative agli altri due lati del triangolo ABC. Quindi, le altezze del triangolo ABC sono gli assi dei lati del triangolo A'B'C', i quali concorrono in un punto.

Osservazione - Nel triangolo acutangolo l'ortocentro è interno al triangolo; nel triangolo rettangolo coincide col vertice dell'angolo retto; nel triangolo ottusangolo è esterno.
Teorema - Le mediane di un triangolo concorrono in un punto che divide ciascuna di esse in due parti delle quali quella che contiene il vertice è doppia dell'altra; tale punto si chiama baricentro.
Nel triangolo ABC si considerano le due mediane AM e BM e sia G il loro punto d'intersezione. Le due mediane s'incontrano sicuramente nel punto G, in quanto gli estremi di ciascuna di esse giacciono da parti opposte rispetto all'altra. Si considera il quadrilatero che ha per vertici M e N, ed i punti medi P e Q, rispettivamente di AG e BG e si dimostra che è un parallelogrammo. Infatti, i lati opposti MN e PQ, che congiungono i punti medi dei lati AC e BC e di AG e BG, essendo paralleli al lato AB e metà di questo, sono uguali fra loro e anche paralleli. Quindi risulta che MNPQ è un parallelogrammo. Segue che PG=GM, e poichè risulta AP=PG, i tre segmenti AP, PG e GM sono uguali fra loro. Ragionando allo stesso modo, risulta anche BQ=QG=GN. Perciò, le due mediane considerate s'incontrano in un punto G, il quale divide ciascuna di esse in due parti di cui una, quella che contiene il vertice, è doppia dell'altra. La terza mediana uscente da C, dovendo dividere ciascuna delle altre due alla stessa maniera, deve necessariamente passare per G, dal quale rimane essa stessa divisa in due parti come AM.

Il baricentro, l'ortocentro, l'incentro e il circocentro si dicono punti notevoli di un triangolo.
In un triangolo equilatero il baricentro, l'ortocentro, l'incentro e il circocentro coincidono in unico punto.
Infatti, in un triangolo equilatero la bisettrice, l'altezza e la mediana relativa ad un lato qualsiasi coincidono e con queste l'asse dello stesso lato.