MIKY & GENNY
MISURA DELLA CIRCONFERENZA E AREA DEL CERCHIO ---> INDICE
Lunghezza della circonferenza
Per determinare la lunghezza di una circonferenza si può ricorrere ad una delle seguenti due costruzioni:
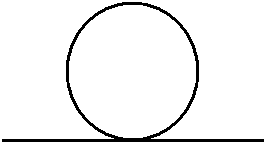
1)-si adagi un filo inestensibile lungo la circonferenza in modo che i suoi estremi si tocchino e poi lo si distenda lungo una retta; il segmento compreso fra gli estremi del filo rappresenta la lunghezza della circonferenza;
2)-Costruito un disco rigido avente lo stesso raggio della circonferenza, lo si appoggi con l'orlo su una retta e si segni il punto A di contatto sia su di esso, sia sulla retta; dopo si faccia rotolare il disco senza strisciare lungo la retta fino a quando il punto A sull'orlo del disco non torni a toccare la retta in un punto B; il segmento AB rappresenta la lunghezza della circonferenza.
Nota bene
Il concetto di lunghezza di una linea è stato assunto come primitivo, cioè senza definizione. Linee di uguale lunghezza si dicono equivalenti.

La determinazione della lunghezza della circonferenza per via sperimentale, come è stato detto, non è conforme ai metodi della geometria razionale, inoltre è impreciso.
Un metodo geometrico che consente un'approssimazione, che teoricamente può essere quella desiderata, è basata sulla considerazione dei poligoni regolari inscritti e circoscritti alla circonferenza.
Si riassume brevemente il modo che si può seguire.
E' evidente che la circonferenza è maggiore del perimetro di qualsiasi poligono inscritto in essa e minore del perimetro di qualsiasi poligono circoscritto. Quanto detto ora, lo si assume come postulato.
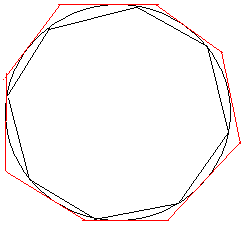
Quindi, se si considerano due poligoni regolari, uno inscritto e l'altro circoscritto, si osserva che man mano che aumenta il numero dei lati, si verifica che i contorni dei due poligoni tendono ad avvicinarsi sempre più alla circonferenza; poichè la circonferenza rimane sempre compresa fra i perimetri di poligoni regolari, inscritti e circoscritti ad essa, la sua lunghezza rimane determinata sempre con maggiore approssimazione, via via che si considerano poligoni con un sempre maggior numero di lati, di modo che scegliendo i due poligoni con un numero di lati sufficientemente grande è possibile raggiungere l'approssimazione desiderata.
Si può quindi dire che:
-come lunghezza di una circonferenza si può assumere un segmento compreso fra i perimetri di due poligoni regolari, uno inscritto e l'altro circoscritto ad essa; l'approssimazione che si può raggiungere aumenta indefinitamente col crescere del numero dei lati di tali poligoni.
Rapporto fra circonferenza e diametro, il numero π
Determinato con sufficiente approssimazione un segmento lungo quanto la circonferenza, per via sperimentale o con più precisione mediante la considerazione dei poligoni regolari inscritti e circoscritti, se si riporta su tale segmento il diametro della circonferenza, si può vedere che questo è contenuto tre volte e rimane una parte, la quale appare poco più lunga di un decimo dello stesso diametro. Ciò significa che il rapporto fra la circonferenza ed il proprio diametro è approssimativamente poco più di di tre e un decimo, cioè è uguale, fino alla prima cifra decimale, a 3,1. Allo stesso risultato si perviene se si ripete l'operazione con circonferenze di diametri diversi.
L'esperienza difficilmente permetterebbe di trovare il rapporto fra una circonferenza e il proprio diametro oltre la prima cifra decimale. Considerazioni teoriche però assicurano che se si potesse spingere l'approssimazione oltre il limite, si vedrebbe che, data una circonferenza qualsiasi, il diametro è contenuto in essa 3 volte più 1 decimo, più 4 centesimi, più 1 millesimo...; non si finirebbe mai, e le cifre decimali non si susseguirebbero neanche periodicamente. Si può quindi affermare che il valore esatto del rapporto fra una circonferenza qualsiasi e il proprio diametro è un numero decimale illimitato non periodico, cioè è un numero irrazionale.
Quindi si può concludere che:
-il rapporto fra la circonferenza e il proprio diametro è costante, cioè non varia al variare della circonferenza, ed è espresso da un numero irrazionale il cui valore approssimato fino alla seconda cifra decimale è 3,14. Tale rapporto si indica con π (pi greco).
Il numero π, o approssimativamente il numero 3,14, indica il rapporto fra una circonferenza qualsiasi e il proprio diametro.
Si può subito dedurre che:
-il valore di π è compreso fra 3 e 4.
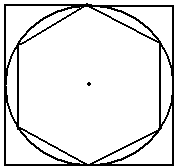
Infatti, il lato dell'esagono regolare inscritto in una circonferenza è uguale al raggio e quindi il suo perimetro è di 6 raggi, ovvero, di 3 diametri; mentre il perimetro del quadrato circoscritto è di 4 diametri. Dunque, una circonferenza è maggiore di 3 diametri e minore di 4 diametri, pertanto il suo rapporto col diametro è compreso fra 3 e 4.
Considerando poligoni regolari inscritti e circoscritti ad una circonferenza Archimede dimostrò che:
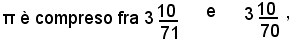
ossia fra
3,140 e 3,142.
In questi ultimi anni, usando le calcolatrici elettroniche, si è oltrepassata la millesima cifra decimale e si va verso la duemillesima. Il valore di π fino alla decima cifra decimale, è dato da:
3,1415928535...
Per la maggior parte dei calcoli pratici si assume:
π = 3,14,
oppure
3,1416.
Talvolta può essere comodo il valore frazionario
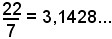
Indicando con r e C le misure del raggio e della circonferenza, per il corollario precedente, si ha:
C : 2r = π,
da cui
Indicando con r, C le misure del raggio e della circonferenza, l'area del triangolo equivalente al cerchio è:
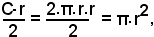
quindi, indicando con A l'area del cerchio, si ha:
A = π r2.
Questa formula esprime la seguente regola:
-l'area del cerchio si ottiene moltiplicando π per il quadrato del raggio.La formula inversa è:
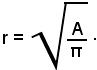
Misura dell'arco e area del settore
Circa la misura degli archi bisogna notare che essi sono delle linee e quindi per la loro misura si sceglie come unità quella dei segmenti in genere. Degli archi, oltre la lunghezza, è importante considerare anche l'ampiezza, il cui significato risulta dalla seguente definizione:
-si chiama ampiezza di un arco l'ampiezza dell'angolo corrispondente.
Da qui risulta che tutti gli archi di grandezza diversa, ma sottesi dallo stesso angolo al centro, hanno la stessa ampiezza.
L'ampiezza di un arco può essere espressa in gradi, e precisamente dallo stesso numero di gradi dell'angolo al centro corrispondente.
Si esaminano ora due principali problemi.
1)-Nota l'ampiezza di un arco ed il suo raggio, determinare la sua lunghezza.
2)-Nota la lunghezza di un arco ed il suo raggio, determinare la sua ampiezza.
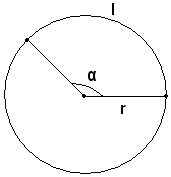
I due problemi si risolvono tenendo presente che gli archi sono proporzionali agli angoli al centro, come si può subito verificare.
Infatti, indicando con l la lunghezza dell'arco di raggio r, con α la sua ampiezza in gradi, sussiste la seguente proporzione:
l : 2πr = α : 360° ,
da cui si ricavano le formule

che risolvono i due problemi.
Se l'ampiezza è data in gradi e minuti primi, oppure in gradi, minuti primi e minuti secondi, nelle formule suddette, tanto α, quanto 180° devono essere ridotti nell'unità dell'ordine più piccolo.
Area del settore
Con le stesse considerazioni fatte per il cerchio, sostituendo ai poligoni regolari inscritti i settori poligonali regolari inscritti nell'arco, si verifica che:
-un settore circolare è equivalente ad un triangolo che ha per base l'arco del settore rettificato e per altezza il raggio.
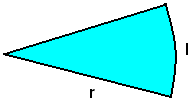
Perciò, indicando con l la lunghezza dell'arco di base del settore ed r il suo raggio, l'area del triangolo equivalente al settore è:
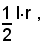
quindi anche per l'area A del settore si ha
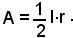
Se dell'arco si conosce l'ampiezza e il raggio, si calcola prima la lunghezza l, come indicato in precedenza, e poi si applica la formula suddetta.
Segmento circolare
Qual'è il geometra che tutto s'affige
Per misurar lo cerchio, e non ritrova,
Pensando, quel principio ond'egli indige
...
Dante allude, in questa similitudine, all'insolubile problema della quadratura del cerchio, cioè al problema dell'esatto rapporto fra la misura del diametro e quello della circonferenza.
Si aggiunge inoltre che non si tratta di impossibilità assoluta come comunemente si crede, ma soltanto all'uso dei due strumenti che si usano nella geometria elementare, in quanto che, usando strumenti atti a tracciare particolari linee, si hanno costruzioni rigorose della rettificazione della circonferenza e della quadratura del cerchio. Sono però interessanti alcune costruzioni approssimate eseguibili col solo uso della riga e del compasso.
Costruzione approssimata di una circonferenza rettificata
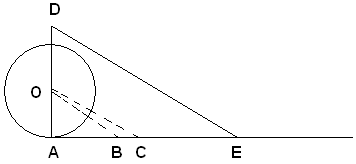
Sia data la circonferenza di centro O e raggio OA. Condotta la tangente in A, su di essa si costruiscono i segmenti consecutivi:
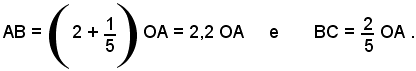
Sulla semiretta AD si prenda AD = AB e da D si conduca la parallela ad OC, che incontra la AC in E. Si dimostra che il segmento AE è, con molta approssimazione, uguale alla circonferenza O.
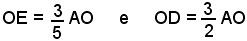
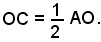
Per determinare la lunghezza di una circonferenza si può ricorrere ad una delle seguenti due costruzioni:

1)-si adagi un filo inestensibile lungo la circonferenza in modo che i suoi estremi si tocchino e poi lo si distenda lungo una retta; il segmento compreso fra gli estremi del filo rappresenta la lunghezza della circonferenza;
2)-Costruito un disco rigido avente lo stesso raggio della circonferenza, lo si appoggi con l'orlo su una retta e si segni il punto A di contatto sia su di esso, sia sulla retta; dopo si faccia rotolare il disco senza strisciare lungo la retta fino a quando il punto A sull'orlo del disco non torni a toccare la retta in un punto B; il segmento AB rappresenta la lunghezza della circonferenza.
Nota bene
Il concetto di lunghezza di una linea è stato assunto come primitivo, cioè senza definizione. Linee di uguale lunghezza si dicono equivalenti.

La determinazione della lunghezza della circonferenza per via sperimentale, come è stato detto, non è conforme ai metodi della geometria razionale, inoltre è impreciso.
Un metodo geometrico che consente un'approssimazione, che teoricamente può essere quella desiderata, è basata sulla considerazione dei poligoni regolari inscritti e circoscritti alla circonferenza.
Si riassume brevemente il modo che si può seguire.
E' evidente che la circonferenza è maggiore del perimetro di qualsiasi poligono inscritto in essa e minore del perimetro di qualsiasi poligono circoscritto. Quanto detto ora, lo si assume come postulato.

Quindi, se si considerano due poligoni regolari, uno inscritto e l'altro circoscritto, si osserva che man mano che aumenta il numero dei lati, si verifica che i contorni dei due poligoni tendono ad avvicinarsi sempre più alla circonferenza; poichè la circonferenza rimane sempre compresa fra i perimetri di poligoni regolari, inscritti e circoscritti ad essa, la sua lunghezza rimane determinata sempre con maggiore approssimazione, via via che si considerano poligoni con un sempre maggior numero di lati, di modo che scegliendo i due poligoni con un numero di lati sufficientemente grande è possibile raggiungere l'approssimazione desiderata.
Si può quindi dire che:
-come lunghezza di una circonferenza si può assumere un segmento compreso fra i perimetri di due poligoni regolari, uno inscritto e l'altro circoscritto ad essa; l'approssimazione che si può raggiungere aumenta indefinitamente col crescere del numero dei lati di tali poligoni.
Rapporto fra circonferenza e diametro, il numero π
Determinato con sufficiente approssimazione un segmento lungo quanto la circonferenza, per via sperimentale o con più precisione mediante la considerazione dei poligoni regolari inscritti e circoscritti, se si riporta su tale segmento il diametro della circonferenza, si può vedere che questo è contenuto tre volte e rimane una parte, la quale appare poco più lunga di un decimo dello stesso diametro. Ciò significa che il rapporto fra la circonferenza ed il proprio diametro è approssimativamente poco più di di tre e un decimo, cioè è uguale, fino alla prima cifra decimale, a 3,1. Allo stesso risultato si perviene se si ripete l'operazione con circonferenze di diametri diversi.
L'esperienza difficilmente permetterebbe di trovare il rapporto fra una circonferenza e il proprio diametro oltre la prima cifra decimale. Considerazioni teoriche però assicurano che se si potesse spingere l'approssimazione oltre il limite, si vedrebbe che, data una circonferenza qualsiasi, il diametro è contenuto in essa 3 volte più 1 decimo, più 4 centesimi, più 1 millesimo...; non si finirebbe mai, e le cifre decimali non si susseguirebbero neanche periodicamente. Si può quindi affermare che il valore esatto del rapporto fra una circonferenza qualsiasi e il proprio diametro è un numero decimale illimitato non periodico, cioè è un numero irrazionale.
Quindi si può concludere che:
-il rapporto fra la circonferenza e il proprio diametro è costante, cioè non varia al variare della circonferenza, ed è espresso da un numero irrazionale il cui valore approssimato fino alla seconda cifra decimale è 3,14. Tale rapporto si indica con π (pi greco).
Il numero π, o approssimativamente il numero 3,14, indica il rapporto fra una circonferenza qualsiasi e il proprio diametro.
Si può subito dedurre che:
-il valore di π è compreso fra 3 e 4.

Infatti, il lato dell'esagono regolare inscritto in una circonferenza è uguale al raggio e quindi il suo perimetro è di 6 raggi, ovvero, di 3 diametri; mentre il perimetro del quadrato circoscritto è di 4 diametri. Dunque, una circonferenza è maggiore di 3 diametri e minore di 4 diametri, pertanto il suo rapporto col diametro è compreso fra 3 e 4.
Considerando poligoni regolari inscritti e circoscritti ad una circonferenza Archimede dimostrò che:
ossia fra
In questi ultimi anni, usando le calcolatrici elettroniche, si è oltrepassata la millesima cifra decimale e si va verso la duemillesima. Il valore di π fino alla decima cifra decimale, è dato da:
Per la maggior parte dei calcoli pratici si assume:
π = 3,14,
oppure
Talvolta può essere comodo il valore frazionario
Indicando con r e C le misure del raggio e della circonferenza, per il corollario precedente, si ha:
C : 2r = π,
da cui
C = 2 π r .
Indicando con d la misura del diametro, essendo:
d = 2 r,
si ha ancheC = π d .
Dunque:
-la misura della circonferenza si trova moltiplicando 2π per la misura del raggio o π per la misura del diametro.
Le formule inverse sono:
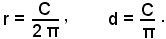
Area del cerchio
Per la determinazione dell'area del cerchio è fondamentale il seguente teorema:
-un cerchio è equivalente ad un triangolo che ha la base lunga quanto la circonferenza e l'altezza uguale al raggio.
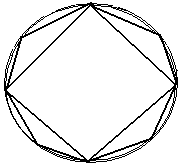
Per verificare questo teorema si considera un poligono regolare inscritto nella circonferenza, per esempio un quadrato, e si suppone di aumentare successivamente i lati, raddoppiandone il numero. Si può osservare che la superficie del poligono tende ad invadere quella del cerchio, in modo che si possa immaginare un poligono regolare inscritto con un numero di lati talmente grande che la differenza fra la superficie del cerchio e quella del poligono risulti minore di una superficie scelta a piacere, per quanto piccola essa sia. Contemporaneamente il contorno del poligono tende a diventare uguale alla circonferenza e l'apotema uguale al raggio. Appare quindi che il cerchio si può considerare come un poligono regolare il cui contorno sia la circonferenza e il cui apotema sia il raggio; poichè un poligono regolare è equivalente ad un triangolo che ha per base il perimetro del poligono e per altezza l'apotema, il teorema resta verificato.
Indicando con d la misura del diametro, essendo:
d = 2 r,
si ha anche
Dunque:
-la misura della circonferenza si trova moltiplicando 2π per la misura del raggio o π per la misura del diametro.
Le formule inverse sono:
Area del cerchio
Per la determinazione dell'area del cerchio è fondamentale il seguente teorema:
-un cerchio è equivalente ad un triangolo che ha la base lunga quanto la circonferenza e l'altezza uguale al raggio.

Per verificare questo teorema si considera un poligono regolare inscritto nella circonferenza, per esempio un quadrato, e si suppone di aumentare successivamente i lati, raddoppiandone il numero. Si può osservare che la superficie del poligono tende ad invadere quella del cerchio, in modo che si possa immaginare un poligono regolare inscritto con un numero di lati talmente grande che la differenza fra la superficie del cerchio e quella del poligono risulti minore di una superficie scelta a piacere, per quanto piccola essa sia. Contemporaneamente il contorno del poligono tende a diventare uguale alla circonferenza e l'apotema uguale al raggio. Appare quindi che il cerchio si può considerare come un poligono regolare il cui contorno sia la circonferenza e il cui apotema sia il raggio; poichè un poligono regolare è equivalente ad un triangolo che ha per base il perimetro del poligono e per altezza l'apotema, il teorema resta verificato.
Indicando con r, C le misure del raggio e della circonferenza, l'area del triangolo equivalente al cerchio è:
quindi, indicando con A l'area del cerchio, si ha:
A = π r2.
Questa formula esprime la seguente regola:
-l'area del cerchio si ottiene moltiplicando π per il quadrato del raggio.
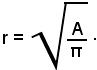
Misura dell'arco e area del settore
Circa la misura degli archi bisogna notare che essi sono delle linee e quindi per la loro misura si sceglie come unità quella dei segmenti in genere. Degli archi, oltre la lunghezza, è importante considerare anche l'ampiezza, il cui significato risulta dalla seguente definizione:
-si chiama ampiezza di un arco l'ampiezza dell'angolo corrispondente.
Da qui risulta che tutti gli archi di grandezza diversa, ma sottesi dallo stesso angolo al centro, hanno la stessa ampiezza.
L'ampiezza di un arco può essere espressa in gradi, e precisamente dallo stesso numero di gradi dell'angolo al centro corrispondente.
Si esaminano ora due principali problemi.
1)-Nota l'ampiezza di un arco ed il suo raggio, determinare la sua lunghezza.
2)-Nota la lunghezza di un arco ed il suo raggio, determinare la sua ampiezza.

I due problemi si risolvono tenendo presente che gli archi sono proporzionali agli angoli al centro, come si può subito verificare.
Infatti, indicando con l la lunghezza dell'arco di raggio r, con α la sua ampiezza in gradi, sussiste la seguente proporzione:
da cui si ricavano le formule
che risolvono i due problemi.
Se l'ampiezza è data in gradi e minuti primi, oppure in gradi, minuti primi e minuti secondi, nelle formule suddette, tanto α, quanto 180° devono essere ridotti nell'unità dell'ordine più piccolo.
Area del settore
Con le stesse considerazioni fatte per il cerchio, sostituendo ai poligoni regolari inscritti i settori poligonali regolari inscritti nell'arco, si verifica che:
-un settore circolare è equivalente ad un triangolo che ha per base l'arco del settore rettificato e per altezza il raggio.

Perciò, indicando con l la lunghezza dell'arco di base del settore ed r il suo raggio, l'area del triangolo equivalente al settore è:
quindi anche per l'area A del settore si ha
Se dell'arco si conosce l'ampiezza e il raggio, si calcola prima la lunghezza l, come indicato in precedenza, e poi si applica la formula suddetta.
Segmento circolare
Definizione - Si chiama segmento circolare la parte del cerchio compresa fra un arco e la corda che esso sottende.
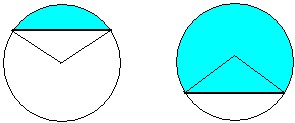
Esso è costituito dalla parte di piano contenuta in semipiano alla cui origine appartiene la corda. L'area del segmento circolare di determina come differenza, o come somma, fra l'area di un settore e l'area di un triangolo.
Corona circolare

Esso è costituito dalla parte di piano contenuta in semipiano alla cui origine appartiene la corda. L'area del segmento circolare di determina come differenza, o come somma, fra l'area di un settore e l'area di un triangolo.
Corona circolare
Definizione - Si chiama corona circolare, la parte porzione di piano compresa fra due circonferenze concentriche.
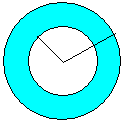
Essa è costituita dall'insieme dei punti che sono esterni alla circonferenza di raggio minore ed interni a quella di raggio maggiore. La sua area è data dalla differenza fra le aree dei cerchi che la delimitano.
Nota bene
Possibilità della rettificazione della circonferenza e della quadratura del cerchio
Si è visto che esiste un solo segmento equivalente ad una circonferenza ed un poligono di superficie determinata equivalente ad un cerchio, ma nulla si è detto sulla possibilità di una loro effettiva costruzione.
Si può affermare che è impossibile, con la riga e con il compasso soltanto, risolvere il problema della rettificazione della circonferenza, e quindi della quadratura del cerchio.
Tale impossibilità, che deriva dal fatto che non si può costruire con l'uso della sola riga e del compasso un segmento che abbia per lunghezza π, venne dimostrata in maniera rigorosa da Lindemann nel 1882, anche se dopo vari tentativi fosse stata intuita da molto tempo.
Un eco si trova anche nella Divina Commedia di Dante Alighieri, Paradiso, XXXIII, 133:

Essa è costituita dall'insieme dei punti che sono esterni alla circonferenza di raggio minore ed interni a quella di raggio maggiore. La sua area è data dalla differenza fra le aree dei cerchi che la delimitano.
Nota bene
Possibilità della rettificazione della circonferenza e della quadratura del cerchio
Si è visto che esiste un solo segmento equivalente ad una circonferenza ed un poligono di superficie determinata equivalente ad un cerchio, ma nulla si è detto sulla possibilità di una loro effettiva costruzione.
Si può affermare che è impossibile, con la riga e con il compasso soltanto, risolvere il problema della rettificazione della circonferenza, e quindi della quadratura del cerchio.
Tale impossibilità, che deriva dal fatto che non si può costruire con l'uso della sola riga e del compasso un segmento che abbia per lunghezza π, venne dimostrata in maniera rigorosa da Lindemann nel 1882, anche se dopo vari tentativi fosse stata intuita da molto tempo.
Un eco si trova anche nella Divina Commedia di Dante Alighieri, Paradiso, XXXIII, 133:
Per misurar lo cerchio, e non ritrova,
Pensando, quel principio ond'egli indige
...
Dante allude, in questa similitudine, all'insolubile problema della quadratura del cerchio, cioè al problema dell'esatto rapporto fra la misura del diametro e quello della circonferenza.
Si aggiunge inoltre che non si tratta di impossibilità assoluta come comunemente si crede, ma soltanto all'uso dei due strumenti che si usano nella geometria elementare, in quanto che, usando strumenti atti a tracciare particolari linee, si hanno costruzioni rigorose della rettificazione della circonferenza e della quadratura del cerchio. Sono però interessanti alcune costruzioni approssimate eseguibili col solo uso della riga e del compasso.
Costruzione approssimata di una circonferenza rettificata
Sia data la circonferenza di centro O e raggio OA. Condotta la tangente in A, su di essa si costruiscono i segmenti consecutivi:
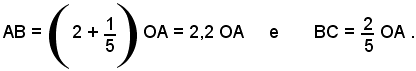
Sulla semiretta AD si prenda AD = AB e da D si conduca la parallela ad OC, che incontra la AC in E. Si dimostra che il segmento AE è, con molta approssimazione, uguale alla circonferenza O.

Infatti, dalla similitudine dei triangoli DAE, OAC, si ha:
AE : AC = AD : AO.
Supposto che il raggio della circonferenza sia uguale ad 1, le lunghezze sei segmenti AC, AD, sono rispettivamente:
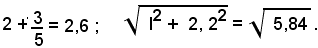
Supposto che il raggio della circonferenza sia uguale ad 1, le lunghezze sei segmenti AC, AD, sono rispettivamente:
Quindi, indicando con x la misura del segmento AE, risulta:
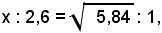
da cui, dopo semplici calcoli, si ottiene
x = 6,283185...
La lunghezza della circonferenza rettificata sarebbe:
cosicchè AE supera la circonferenza di meno di due milionesimi del raggio.La lunghezza della circonferenza rettificata sarebbe:
2π = 6,283185...
Costruzione approssimata del quadrato equivalente ad un cerchio
Sul diametro AB di un cerchio di centro O, a partire da O e da bande opposte, si portino i segmenti
Sul diametro AB di un cerchio di centro O, a partire da O e da bande opposte, si portino i segmenti
e dalla stessa banda un segmento
Descritte
da bande opposte ad AB due semicirconferenze di diametri EC ed AD, si
conduca la perpendicolare ad AB in O, la quale incontri in F e
in G le due semicirconferenze.
Si dimostra che il quadrato di lato FG è approssimativamente equivalente al cerchio dato.
Infatti, si ha:
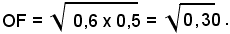

Inoltre le lunghezze dei segmenti OA e OD sono 1 e 1,5 e quindi
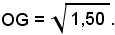
Ora la lunghezza del lato del quadrato equivalente ad un cerchio di raggio 1 è:
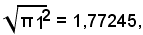
quindi FG supera questo lato di meno di due centomillesimi del raggio.
Si dimostra che il quadrato di lato FG è approssimativamente equivalente al cerchio dato.
Infatti, si ha:
OE : OF = OF : OC
e quindie
OA : OG = OG : OD .
Supposta uguale ad 1 la lunghezza del raggio del cerchio, le lunghezze dei segmenti OE, OC sono rispettivamente
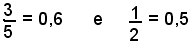

Perciò:
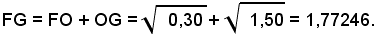
Ora la lunghezza del lato del quadrato equivalente ad un cerchio di raggio 1 è:
quindi FG supera questo lato di meno di due centomillesimi del raggio.