MIKY & GENNY

POLIGONI INSCRITTI E CIRCOSCRITTI ---> INDICE

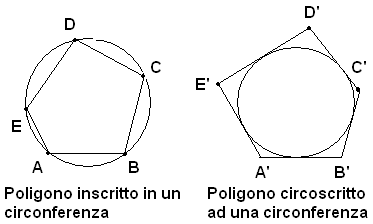
POLIGONI INSCRITTI IN UNA CIRCONFERENZA

Un poligono si dice inscritto in una circonferenza quando i suoi vertici stanno su di essa. In tale caso, la circonferenza si dice circoscritta al poligono.

POLIGONI CIRCOSCRITTI AD UNA CIRCONFERENZA

Un poligono si dice circoscritto ad una circonferenza quando i suoi lati sono tangenti ad essa.
In tale caso, la circonferenza si dice inscritta al poligono.

Nelle figure seguenti il poligono ABCDE è un poligono inscritto in una circonferenza, mentre A'B'C'D'E' è circoscritto.

Affinchè un poligono si possa circoscrivere ad una circonferenza, occorre e basta che esista un punto che abbia la stessa distanza da tutti i lati del poligono, ossia che le bisettrici dei suoi angoli interni passino per uno stesso punto.

Affinchè un poligono si possa inscrivere in una circonferenza, è necessario e sufficiente che esista un punto che abbia la stessa distanza da tutti i vertici del poligono, ossia che gli assi dei suoi lati concorrano in uno stesso punto.

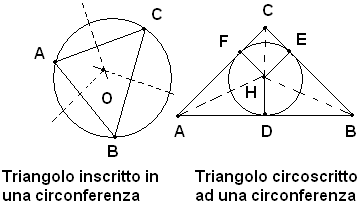
Teorema - Ad ogni triangolo si può sempre inscrivere e circoscrivere una circonferenza.
Infatti, come è noto, gli assi dei lati del triangolo ABC concorrono in un punto O, circocentro, che ha uguale distanza dai vertici. Di conseguenza, la circonferenza di centro O e raggio OA passa per gli altri due vertici. Essa è dunque circoscritta al triangolo. Inoltre, le bisettrici degli angoli del triangolo concorrono in un punto H che ha uguale distanza dai lati, incentro. Dunque la circonferenza che ha centro nell'incentro ed è tangente ad uno dei lati del triangolo, è tangente agli altri due lati. Pertanto, essa è la circonferenza inscritta.

QUADRANGOLI INSCRITTIBILI E CIRCOSCRITTIBILI

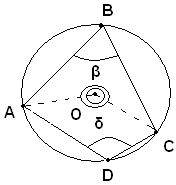
Teorema - In ogni quadrangolo inscritto in un cerchio, gli angoli opposti sono supplementari.
Ipotesi: il quadrangolo ABCD è inscritto in una circonferenza di centro O.
Tesi: si vuole dimostrare che gli angoli opposti, β e δ sono supplementari.
Dimostrazione
Infatti, l'angolo β è metà dell'angolo, convesso, di centro O e lati OA e OC e l'angolo δ è metà dell'angolo al centro, concavo, di centro O e lati OA e OC. Quindi la somma degli angoli β e δ è uguale alla metà dell'intero angolo giro in O, cioè è uguale ad un angolo piatto; i due angoli sono dunque supplementari, come volevasi dimostrare.

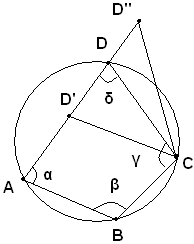
Teorema - Un quadrangolo con due angoli supplementari è inscrittibile in un cerchio.
Ipotesi: nel quadrangolo ABCD gli angoli opposti α e γ (e quindi β e δ) sono supplementari.
Tesi: si vuole dimostrare che il quadrangolo ABCD è inscrittibile in una circonferenza, ossia che la circonferenza passante per per i tre punti A, B e C passa anche per D.
Dimostrazione
Infatti, ragionando per assurdo, si suppone che la circonferenza passa per per i tre punti A, B e C e non passa per D. In tal caso la circonferenza taglia il lato AD, oppure il suo prolungamento. Se taglia AD in un punto D', l'angolo di vertice D' e lati D'A e D'C, per il teorema precedente, è supplementare di B, ma essendo per ipotesi anche δ supplementare di B, risulta l'angolo di vertice D' e lati D'A e D'C uguale a δ. D'altra parte, essendo l'angolo vertice D' e lati D'A e D'C esterno al triagolo DD'C, è maggiore dell'angolo δ, e ciò è assurdo. Ragionando in modo analogo, se la circonferenza taglia il prolungamento del lato AD in un punto D'', si perviene anche ad un assurdo, cioè che l'angolo di vertice D'' e lati D''A e D''C è contemporaneamente uguale e minore dell'angolo δ. La circonferenza, non potendo tagliare nè il lato AD, in un punto interno, nè il prolungamento, deve necessariamente passare per D.

Teorema - In ogni quadrangolo circoscritto ad una circonferenza la somma dei due lati opposti è uguale alla somma degli altri due. Viceversa, un quadrangolo in cui la somma dei due lati opposti è uguale alla somma degli altri due, è circoscrittibile ad una circonferenza
Si omette la dimostrazione.