MIKY & GENNY
POLIGONI REGOLARI ---> INDICE
TEOREMI
1)-Ogni poligono regolare ammette una circonferenza inscritta e una circoscritta.
Dimostrazione
Sia ABCDE un poligono regolare. Si tracciano le bisettrici di due angoli consecutivi in A e in B; esse devono incontrarsi in un punto O. Il triangolo AOB è isoscele, perchè gli angoli alla base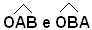
sono uguali per essere la metà degli angoli in
A e in B. Si congiunge poi O con C; Il triangolo BOC risulta uguale al
triangolo AOB, perchè BO è comune ai due triangoli; AB=BC,
perchè lati del poligono regolare ed 
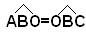, essendo BO bisettrice dell'angolo 
Segue
che AO=OB e OB=OC, e ciò prova che il punto O è
equidistante dai vertici A, B e C del poligono. Analogamente si prova
che esso è ancora equidistante dagli altri vertici. Resta
così dimostrato che la circonferenza di centro O e raggio OA
è circoscritta al poligono. Poichè inoltre i lati di
questo sono corde uguali, e pertanto equidistanti dal centro, la
circonferenza di centro O e di raggio uguale alla distanza comune OF
risulta tangente a tutti i lati, ossia è inscritta al poligono.
Osservazione
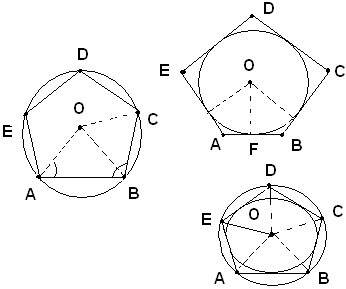
Dal teorema precedente risulta che i due cerchi, inscritto e circoscritto, hanno lo stesso centro, che si chiama centro del poligono regolare. Il raggio del cerchio circoscritto si chiama raggio del poligono. Il raggio del cerchio inscritto si chiama apotema.
1)-Ogni poligono regolare ammette una circonferenza inscritta e una circoscritta.
Dimostrazione
Sia ABCDE un poligono regolare. Si tracciano le bisettrici di due angoli consecutivi in A e in B; esse devono incontrarsi in un punto O. Il triangolo AOB è isoscele, perchè gli angoli alla base
sono uguali per essere la metà degli angoli in
A e in B. Si congiunge poi O con C; Il triangolo BOC risulta uguale al
triangolo AOB, perchè BO è comune ai due triangoli; AB=BC,
perchè lati del poligono regolare ed , essendo BO bisettrice dell'angolo Segue
che AO=OB e OB=OC, e ciò prova che il punto O è
equidistante dai vertici A, B e C del poligono. Analogamente si prova
che esso è ancora equidistante dagli altri vertici. Resta
così dimostrato che la circonferenza di centro O e raggio OA
è circoscritta al poligono. Poichè inoltre i lati di
questo sono corde uguali, e pertanto equidistanti dal centro, la
circonferenza di centro O e di raggio uguale alla distanza comune OF
risulta tangente a tutti i lati, ossia è inscritta al poligono.Osservazione
Dal teorema precedente risulta che i due cerchi, inscritto e circoscritto, hanno lo stesso centro, che si chiama centro del poligono regolare. Il raggio del cerchio circoscritto si chiama raggio del poligono. Il raggio del cerchio inscritto si chiama apotema.
2)-Un poligono equilatero inscritto in una circonferenza è regolare ed è altresì regolare il poligono avente per lati consecutivi le tangenti ai suoi vertici.
Dimostrazione
Il poligono ABCDE inscritto in una circonferenza ha i lati uguali; sono uguali allora anche gli archi sottesi, e quindi anche la somma di due successivi di questi archi, si ha: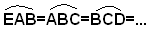
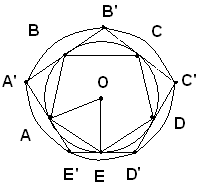
Ma allora anche gli angoli in A, in B, in C,... inscritti in quegli archi, sono uguali. Il poligono è quindi equiangolo, e siccome per ipotesi è equilatero, è regolare. Se ora si conducono le tangenti alla circonferenza nei vertici del poligono inscritto, si ottiene il poligono circoscritto A'B'C'D'E'. I triangoli AA'B, BB'C, CC'D,... sono isosceli e uguali fra loro, perchè hanno i lati AB, BC e CD,... uguali per ipotesi, e uguali tutti gli angoli adiacenti a tali lati, perchè angoli alla circonferenza che insistono su archi uguali. Segue che sono uguali gli angoli in A, in B, in C,... e i lati AA', BB', CC',... e quindi i loro doppi, E'A', A'B', B'C',... Il poligono A'B'C'D'E' è perciò equilatero ed equiangolo e quindi regolare.
Dimostrazione
Il poligono ABCDE inscritto in una circonferenza ha i lati uguali; sono uguali allora anche gli archi sottesi, e quindi anche la somma di due successivi di questi archi, si ha:
Ma allora anche gli angoli in A, in B, in C,... inscritti in quegli archi, sono uguali. Il poligono è quindi equiangolo, e siccome per ipotesi è equilatero, è regolare. Se ora si conducono le tangenti alla circonferenza nei vertici del poligono inscritto, si ottiene il poligono circoscritto A'B'C'D'E'. I triangoli AA'B, BB'C, CC'D,... sono isosceli e uguali fra loro, perchè hanno i lati AB, BC e CD,... uguali per ipotesi, e uguali tutti gli angoli adiacenti a tali lati, perchè angoli alla circonferenza che insistono su archi uguali. Segue che sono uguali gli angoli in A, in B, in C,... e i lati AA', BB', CC',... e quindi i loro doppi, E'A', A'B', B'C',... Il poligono A'B'C'D'E' è perciò equilatero ed equiangolo e quindi regolare.