MIKY & GENNY
PROPORZIONI FRA GRANDEZZE ---> INDICE
Proporzionalità fra coppi di grandezze
Definizione - Si dice che quattro grandezze in un certo ordine formano una proporzione, se il rapporto fra la prima e la seconda è uguale al rapporto fra la terza e la quarta.
E' sottinteso che la prima grandezza è omogenea alla seconda e la terza alla quarta.
Esempi
1)-Siano dati 4 segmenti a, b, a', b':
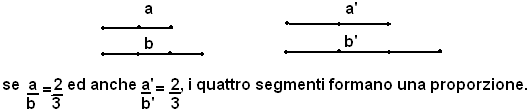
1)-Siano dati i segmenti a, b, il cui rapporto è 3/4 e gli angoli α, β il cui rapporto è anche 3/4: essi sono in proporzione.

La proporzione fra quattro grandezze A, B, C, D, si scrive:
A : B = C : D
e si legge A sta a B come C sta a D.
Le quattro grandezze A, B, C, D, si dicono termini della proporzione, A e C antecedenti, B e D conseguenti, B e C medi, A e D estremi, D quarto proporzionale dopo A, B, C.
Dovendo esprimere che quattro grandezze A, B, C, D, sono proporzionali si dice anche che A e B stanno fra loro come C e D, oppure anche A e B sono proporzionali a C e D.
Le grandezze A e B, nell'ordine scritto, si chiamano coppie di grandezze e se le due coppie di grandezze formano una proporzione, si dice che la prima coppia è proporzionale alla seconda.
Se i medi di una proporzione sono uguali, la proporzione si dice continua, il medio si chiama medio proporzionle fra le due grandezze estreme; l'ultimo si chiama terzo proporzionale.
Teorema - Se quattro grandezze formano una proporzione, anche le loro misure rispetto ad una unità presa ad arbitrio, formano una proporzione; e viceversa.
Sia data la proporzione:
A : B = C : D
e siano rispettivamente α, β, γ, δ, le misure di A, B, C, D rispetto all'unità U. Si deve dimostrare che:
α : β = γ : δ
Infatti, essendo il rapporto fra due grandezze uguale al rapporto delle loro misure, si ha:
A : B = α : β, C : D = γ : δ
ed essendo inoltre per ipotesi
A : B = C : D,
risulta anche
α : β = γ : δ.
Viceversa, se
α : β = γ : δ,
si ha:
α : β = A : B , γ : δ = C : D
ed essendo per ipotesi
α : β = γ : δ,
risulta
A : B = C : D,
come volevasi dimostrare.
Nota bene
Questo teorema permette di trasportare alle proporzioni fra grandezze le proprietà delle proporzioni fra numeri, pertanto si evita la dimostrazione diretta.
Da una proporzione fra grandezze si passa, sostituendo ad esse le loro misure, ad una proporzione fra numeri; si opera su questa secondo le regole già note dall'aritmetica e infine si ritorna ad una proporzione fra grandezze. Di seguito sono riportate le proprietà più importanti.
Relazioni fra grandezze di una stessa proporzione
1)-Una coppia di grandezze è proporzionale a se stessa, cioè:
A : B = A : B.
2)-Se una coppia di grandezze è proporzionale ad un'altra, questa è proporzionale alla prima, cioè se:
A : B = C : D
è anche
C : D = A : B.
3)-Due coppie di grandezze proporzionali ad una terza sono proporzionali fra loro.
Cioè se:
4)-Se quattro grandezze sono in proporzione, la stessa relazione di uguaglianza o disuguaglianza che passa fra la prima e la seconda passa fra la terza e la quarta e, se sono tutte omogenee, la stessa relazione di uguaglianza o disuguaglianza che passa fra gli antecedenti passa anche fra i conseguenti.
Cioè se:
A : B = C : D,
a seconda che:
A=B è anche C=D,
A<B è anche C<D,
A>B è anche C>D,
A=C è anche B=D,
A<C è anche B<D,
A>C è anche B>D.
Proporzioni dedotte da una proporzione assegnata
Se due coppie di grandezze formano una proporzione, moltiplicando una di esse per un numero razionale, si ottiene una seconda proporzione.
Cioè se:
A : B = C : D,
è anche
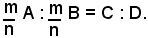
B : A = D : C.
A : C = B : D.
oppure
D : B = C : A.
Componendo - Se quattro grandezze sono in proporzione, la somma delle prime due sta alla seconda, oppure alla prima, come la somma delle ultime due sta alla quarta, oppure alla terza.
Cioè se:
A : B = C : D,
si ha anche
(A + B) : B = (C + D) : D
oppure
(A + B) : A = (C + D) : C.
Dividendo - Se quattro grandezze sono in proporzione, la differenza delle prime due sta alla seconda, oppure alla prima, come la differenza delle ultime due sta alla quarta, oppure alla terza.
Cioè se:
A : B = C : D,
si ha anche
(A - B) : B = (C - D) : D
oppure
(A - B) : A = (C - D) : C.
Unicità del quarto e del medio proporzionale
Il quarto proporzionale dopo tre grandezze date è unico.
Cioè se:
A : B = C : D e A : B = C : D',
dev'essere
D = D'.
Il medio proporzionale fra due grandezze date è unico.Cioè se:
A : H = H : B e A : K = K : B,
si ha
H = K.
Proporzionalità fra coppie di grandezze
L'uguaglianza di più rapporti si dice catena di rapporti. I primi termini dei rapporti si chiamano antecedenti, i secondi conseguenti.
Proprietà - In una catena di rapporti fra grandezze tutte omogenee, la somma degli antecedenti sta alla somma dei conseguenti come un antecedente sta al proprio conseguente.
A : B = C : D = E : F,
si ha anche
(A + C + E) : (B + D + F) = A : B.
Proporzionalità fra classi di grandezze
Due classi di grandezze si dicono direttamente proporzionali quando ad ogni grandezza di una classe corrisponde una ed una sola grandezza dell'altra ed inoltre, il rapporto di due qualsiasi grandezze di una classe è uguale al rapporto delle corrispondenti grandezze dell'altra classe.
Le grandezze di una delle classi possono essere omogenee o no con quelle dell'altra.
Così, date le due classi di grandezze:
A, B, C, D ...
A', B', C', D' ...
se ad A corrispode A', a B, B', ecc., ed inoltre si hanno le proporzioni
A : B = A' : B'
A : C = A' : C', ecc.
le due classi sono proporzionali ed in tal caso si scrive:
A : B : C : D : ... = A' : B' : C' : D' : ...
Due grandezze corrispondenti in due classi direttamente proporzionali si dicono omologhe.
Criterio generale di proporzionalità fra classi di grandezze
Siccome per decidere della proporzionalità fra due classi di grandezze occorre verificare l'uguaglianza di rapporti, dal criterio di uguaglianza di rapporti si trae senz'altro il seguente criterio di proporzionalità fra due classi di grandezze.
Due classi di grandezze sono direttamente proporzionali se i valori per difetto, o per eccesso, del rapporto fra due grandezze qualsiasi della prima classe sono anche rispettivamente valori per difetto, o per eccesso, del rapporto fra le due grandezze corrispondenti nell'altra classe.
Esempi di classi direttamente proporzionali
1)-I rettangoli aventi la stessa altezza e le loro basi formano due classi direttamente proporzionali.
Infatti, si è dimostrato in precedenza che i rettangoli aventi la stessa altezza hanno lo stesso rapporto delle rispettive basi.
2)-Gli archi di una stessa circonferenza ed i rispettivi angoli al centro formano due classi direttamente proporzionali.
Basta dimostrare che il rapporto di due archi qualsiasi di una circonferenza è uguale a quello dei corrispondenti angoli al centro.
Proprietà delle proporzioni fra segmenti
Teorema - Se quattro segmenti formano una proporzione, il rettangolo dei medi è equivalente a quello degli estremi. Viceversa, se quattro segmenti in un certo ordine sono tali che il rettangolo dei medi è equivalente a quello degli estremi, i quattro segmenti formano una proporzione.
Siano a, b, c, d quattro segmenti che formano una proporzione, quindi:
a : b = c : d.
Indicando con r(a, d) il rettangolo avente per dimensioni a e d, si deve dimostrare che:
r(a, d) = r(b, c).
Siano α, β, γ, δ le misure dei quattro segmenti, dalla proporzione fra segmenti, si ricava quella fra le loro misure:
α : β = γ : δ,
da cuiαδ = βγ;
cioè l'area del r(a, d) è uguale a quella del r(b, c) e ciò dimostra che i due rettangoli sono equivalenti.
Viceversa: se r(a, d) è equivalente a r(b, c), dev'essere:
αδ = βγ,
da cui si ha la proporzione fra la misura dei segmenti
α : β = γ : δ
e quindi sussiste anche la proporzione fra i segmenti
a : b = c : d.
Corollario - Se un segmento è medio proporzionale fra altri due, il quadrato costruito su di esso è equivalente al rettangolo costruito sugli altri due; e viceversa.
Teorema - Se quattro segmenti sono in proporzione, anche i quadrati costruiti su di essi sono in proporzione.
q(A) : q(b) = q(c) : q(d).
Infatti fra le misure α, β, γ, δ dei quattro segmenti sussiste la proporzione:
α : β = γ : δ,
da cui
α2 : β2 = γ2 : δ2
e ciò prova che le aree dei quadrati costruiti sui quattro segmenti sono in proporzione. Allora anche gli stessi quadrati sono in proporzione.
Definizione - Si dice che quattro grandezze in un certo ordine formano una proporzione, se il rapporto fra la prima e la seconda è uguale al rapporto fra la terza e la quarta.
E' sottinteso che la prima grandezza è omogenea alla seconda e la terza alla quarta.
Esempi
1)-Siano dati 4 segmenti a, b, a', b':

1)-Siano dati i segmenti a, b, il cui rapporto è 3/4 e gli angoli α, β il cui rapporto è anche 3/4: essi sono in proporzione.

La proporzione fra quattro grandezze A, B, C, D, si scrive:
A : B = C : D
e si legge A sta a B come C sta a D.
Le quattro grandezze A, B, C, D, si dicono termini della proporzione, A e C antecedenti, B e D conseguenti, B e C medi, A e D estremi, D quarto proporzionale dopo A, B, C.
Dovendo esprimere che quattro grandezze A, B, C, D, sono proporzionali si dice anche che A e B stanno fra loro come C e D, oppure anche A e B sono proporzionali a C e D.
Le grandezze A e B, nell'ordine scritto, si chiamano coppie di grandezze e se le due coppie di grandezze formano una proporzione, si dice che la prima coppia è proporzionale alla seconda.
Se i medi di una proporzione sono uguali, la proporzione si dice continua, il medio si chiama medio proporzionle fra le due grandezze estreme; l'ultimo si chiama terzo proporzionale.
Teorema - Se quattro grandezze formano una proporzione, anche le loro misure rispetto ad una unità presa ad arbitrio, formano una proporzione; e viceversa.
Sia data la proporzione:
A : B = C : D
e siano rispettivamente α, β, γ, δ, le misure di A, B, C, D rispetto all'unità U. Si deve dimostrare che:
Infatti, essendo il rapporto fra due grandezze uguale al rapporto delle loro misure, si ha:
A : B = α : β, C : D = γ : δ
ed essendo inoltre per ipotesi
risulta anche
α : β = γ : δ.
Viceversa, se
α : β = γ : δ,
si ha:
α : β = A : B , γ : δ = C : D
ed essendo per ipotesi
α : β = γ : δ,
risulta
A : B = C : D,
come volevasi dimostrare.
Nota bene
Questo teorema permette di trasportare alle proporzioni fra grandezze le proprietà delle proporzioni fra numeri, pertanto si evita la dimostrazione diretta.
Da una proporzione fra grandezze si passa, sostituendo ad esse le loro misure, ad una proporzione fra numeri; si opera su questa secondo le regole già note dall'aritmetica e infine si ritorna ad una proporzione fra grandezze. Di seguito sono riportate le proprietà più importanti.
Relazioni fra grandezze di una stessa proporzione
1)-Una coppia di grandezze è proporzionale a se stessa, cioè:
2)-Se una coppia di grandezze è proporzionale ad un'altra, questa è proporzionale alla prima, cioè se:
A : B = C : D
è anche
C : D = A : B.
3)-Due coppie di grandezze proporzionali ad una terza sono proporzionali fra loro.
Cioè se:
A : B = H : K e C : D = H : K,
è anche
A : B = C : D.
è anche
A : B = C : D.
4)-Se quattro grandezze sono in proporzione, la stessa relazione di uguaglianza o disuguaglianza che passa fra la prima e la seconda passa fra la terza e la quarta e, se sono tutte omogenee, la stessa relazione di uguaglianza o disuguaglianza che passa fra gli antecedenti passa anche fra i conseguenti.
Cioè se:
a seconda che:
A=C è anche B=D,
A<C è anche B<D,
A>C è anche B>D.
Proporzioni dedotte da una proporzione assegnata
Se due coppie di grandezze formano una proporzione, moltiplicando una di esse per un numero razionale, si ottiene una seconda proporzione.
Cioè se:
A : B = C : D,
è anche
Invertendo - Se in una proporzione si scambiano gli antecedenti con i conseguenti, si ottiene ancora una proporzione.
Cioè se:
A : B = C : D,
è anche
Cioè se:
è anche
Permutando
- Se in una proporzione fra grandezze tutte omogenee si scambiano
i medi con gli estremi, si ottiene ancora una proporzione.
Cioè se:
A : B = C : D,
e A, B, C, D sono grandezze della stessa specie, si ha anche
Cioè se:
A : B = C : D,
e A, B, C, D sono grandezze della stessa specie, si ha anche
A : C = B : D.
oppure
D : B = C : A.
Componendo - Se quattro grandezze sono in proporzione, la somma delle prime due sta alla seconda, oppure alla prima, come la somma delle ultime due sta alla quarta, oppure alla terza.
Cioè se:
si ha anche
(A + B) : B = (C + D) : D
oppure
Dividendo - Se quattro grandezze sono in proporzione, la differenza delle prime due sta alla seconda, oppure alla prima, come la differenza delle ultime due sta alla quarta, oppure alla terza.
Cioè se:
A : B = C : D,
si ha anche
oppure
(A - B) : A = (C - D) : C.
Unicità del quarto e del medio proporzionale
Il quarto proporzionale dopo tre grandezze date è unico.
Cioè se:
dev'essere
Il medio proporzionale fra due grandezze date è unico.
si ha
H = K.
Proporzionalità fra coppie di grandezze
L'uguaglianza di più rapporti si dice catena di rapporti. I primi termini dei rapporti si chiamano antecedenti, i secondi conseguenti.
Proprietà - In una catena di rapporti fra grandezze tutte omogenee, la somma degli antecedenti sta alla somma dei conseguenti come un antecedente sta al proprio conseguente.
A : B = C : D = E : F,
si ha anche
(A + C + E) : (B + D + F) = A : B.
Proporzionalità fra classi di grandezze
Due classi di grandezze si dicono direttamente proporzionali quando ad ogni grandezza di una classe corrisponde una ed una sola grandezza dell'altra ed inoltre, il rapporto di due qualsiasi grandezze di una classe è uguale al rapporto delle corrispondenti grandezze dell'altra classe.
Le grandezze di una delle classi possono essere omogenee o no con quelle dell'altra.
Così, date le due classi di grandezze:
A, B, C, D ...
A', B', C', D' ...
se ad A corrispode A', a B, B', ecc., ed inoltre si hanno le proporzioni
A : B = A' : B'
A : C = A' : C', ecc.
le due classi sono proporzionali ed in tal caso si scrive:
A : B : C : D : ... = A' : B' : C' : D' : ...
Due grandezze corrispondenti in due classi direttamente proporzionali si dicono omologhe.
Criterio generale di proporzionalità fra classi di grandezze
Siccome per decidere della proporzionalità fra due classi di grandezze occorre verificare l'uguaglianza di rapporti, dal criterio di uguaglianza di rapporti si trae senz'altro il seguente criterio di proporzionalità fra due classi di grandezze.
Due classi di grandezze sono direttamente proporzionali se i valori per difetto, o per eccesso, del rapporto fra due grandezze qualsiasi della prima classe sono anche rispettivamente valori per difetto, o per eccesso, del rapporto fra le due grandezze corrispondenti nell'altra classe.
Esempi di classi direttamente proporzionali
1)-I rettangoli aventi la stessa altezza e le loro basi formano due classi direttamente proporzionali.
Infatti, si è dimostrato in precedenza che i rettangoli aventi la stessa altezza hanno lo stesso rapporto delle rispettive basi.
2)-Gli archi di una stessa circonferenza ed i rispettivi angoli al centro formano due classi direttamente proporzionali.
Basta dimostrare che il rapporto di due archi qualsiasi di una circonferenza è uguale a quello dei corrispondenti angoli al centro.
Proprietà delle proporzioni fra segmenti
Teorema - Se quattro segmenti formano una proporzione, il rettangolo dei medi è equivalente a quello degli estremi. Viceversa, se quattro segmenti in un certo ordine sono tali che il rettangolo dei medi è equivalente a quello degli estremi, i quattro segmenti formano una proporzione.
Siano a, b, c, d quattro segmenti che formano una proporzione, quindi:
Indicando con r(a, d) il rettangolo avente per dimensioni a e d, si deve dimostrare che:
Siano α, β, γ, δ le misure dei quattro segmenti, dalla proporzione fra segmenti, si ricava quella fra le loro misure:
da cui
cioè l'area del r(a, d) è uguale a quella del r(b, c) e ciò dimostra che i due rettangoli sono equivalenti.
Viceversa: se r(a, d) è equivalente a r(b, c), dev'essere:
αδ = βγ,
da cui si ha la proporzione fra la misura dei segmenti
e quindi sussiste anche la proporzione fra i segmenti
Corollario - Se un segmento è medio proporzionale fra altri due, il quadrato costruito su di esso è equivalente al rettangolo costruito sugli altri due; e viceversa.
Teorema - Se quattro segmenti sono in proporzione, anche i quadrati costruiti su di essi sono in proporzione.
Siano a, b, c, d quattro segmenti che formano una proporzione, quindi:
a : b = c : d,
SI deve dimostrare che:
SI deve dimostrare che:
Infatti fra le misure α, β, γ, δ dei quattro segmenti sussiste la proporzione:
da cui
e ciò prova che le aree dei quadrati costruiti sui quattro segmenti sono in proporzione. Allora anche gli stessi quadrati sono in proporzione.