MIKY & GENNY
RETTE E PIANI NELLO SPAZIO E PERPENDICOLARITA' ---> INDICE
Si chiama spazio l'insieme di tutti i punti.
Finora sono state trattate le figure piane, ora si passa allo studio delle figure solide, ossia quelle in cui i punti non sono tutti contenuti nello stesso piano.
Ai postulati di appartenenza e al postulato della partizione del piano, si aggiunge il seguente postulato.
Postulato della partizione dello spazio
Ogni piano α divide lo spazio in due parti chiamate semispazi, tali che il segmento che congiunge due punti dello stesso semispazio non ha punti in comune con il piano α, mentre il segmento che congiunge due punti di semispazi diversi ha un punto in comune.
ll piano α si chiama contorno e i punti si considerano come appartenenti all'uno o all'altro semispazio.
Due punti si dicono dalla stessa banda o da bande opposte in un piano α a seconda che giacciono o no in uno solo dei semispazi individuati da α.
Si ha subito che:
semirette e semipiani, aventi l'origine sul contorno di un semipiano e passanti per un punto interno a questo, hanno tutti i punti interni al semispazio.
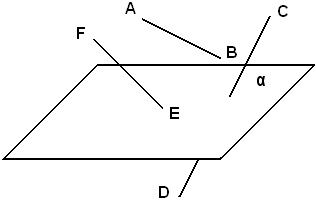
Nella figura suddetta risulta che:
-A e B stanno da una stessa parte,
-C e D stanno da parti opposte rispetto al piano α,
-la semiretta EF, con l'origine E sul piano α, sta da una stessa parte rispetto ad α.
Teorema - Se due piani hanno un punto in comune, hanno in comune una retta che passa per quel punto.
Siano α e β due piani aventi in comune il punto P.
Si deve dimostrare che α e β hanno in comune una retta passante per P.
Infatti, due rette distinte a e b, giacenti nel piano α e passanti per P, sono divise da P in semirette giacenti da bande opposte rispetto a β. Pertanto, sulle rette a e b si possono prendere rispettivamente due punti A e B da bande opposte a β; la congiungente AB interseca β in un punto Q, che è distinto da P; diversamente i punti A, P e B apparterrebbero alla stessa retta, e quindi a e b coinciderebbero. Perciò il punto Q appartiene al piano α, perchè la retta AB giace su α e appartiene al piano perchè β perchè AB interseca β. La retta PQ, avendo i suoi punti situati tanto su α quanto su β, appartiene ad entrambi i piani. Questi non possono avere alcuna retta in comune, altrimenti coinciderebbero.
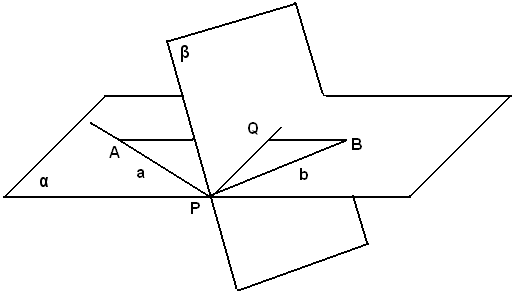
Se due piani hanno una retta in comune, si dice che si tagliano o si segano lungo quella retta, la quale si chiama intersezione dei due piani.
Definizione - Due piani che si segano lungo una retta dividono lo spazio in quattro parti, ognuna delle quali si chiama angolo diedro o semplicemente diedro.
Il diedro si può considerare come costituito dall'insieme dei punti comuni a due semispazi i cui contorni s'incontrano lungo la retta.
Secondo la definizione generale di uguaglianza delle figure, due diedri sono uguali quando è possibile farli coincidere punto per punto.
Dai postulati fondamentali si deducono le seguenti mutue posizioni fra rette e piani:
1)-rette e piani - Dati una una retta e un piano nello spazio, si ha che:
a)-o la retta ha due punti distinti in comune con il piano, e allora tutta la retta giace nel piano;
b)-o ha un solo punto in comune, interseca il piano, ed è divisa dallo stesso in due semirette che giacciono nei semispazi opposti che hanno per contorno il piano;
c)-o non ha nessun punto in comune con il piano, e si vedrà in seguito che ciò è possibile, e si dirà che la retta è parallela al piano;
2)-piani - Due piani nello spazio:
a)-o hanno tre punti in comune, non in linea retta, e coincidono;
b)-o hanno due o un solo punto in comune e hanno in comune una retta che passa per quei punti e si dicono incidenti o secanti;
c)-o non hanno nessun punto in comune, e si vedrà in seguito che ciò è possibile, e si dirà che i due piani sono paralleli;
3)-rette - Due rette nello spazio:
a)-o hanno due punti in comune e allora coincidono;
b)-o hanno un solo punto in comune;
c)-o non hanno nessun punto in comune, e in tal caso giacciono in uno stesso piano e sono parallele, o non giacciono in uno stesso piano e si dicono sghembe.
Sono sghembe, ad esempio, due rette di cui una giace in un piano α e l'altra interseca il piano in un punto fuori dalla retta, come a e b nella figura seguente.
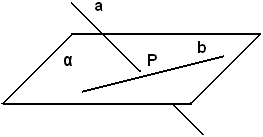
Rette e piani perpendicolari
Definizione - Una retta e un piano si dicono perpendicolari quando la retta incontra il piano ed è perpendicolare a tutte le rette del piano passanti per il punto di intersezione. Questo punto si chiama piede della perpendicolare.
Teorema fondamentale sulla perpendicolarità - Se una retta è perpendicolare a due rette di un piano, passanti per la sua intersezione con il piano, è anche perpendicolare a tutte le altre rette del piano che passano per la stessa intersezione e quindi è perpendicolare al piano.
Una retta r incontri il piano α in un punto O e risulti perpendicolare alle due rette a e b che appartengono ad α.
Si deve dimostrare che la retta r è perpendicolare a qualsiasi retta c uscente da O e giacente nel piano α.
Infatti, sulle rette a e b si prendono rispettivamente i punti A, e B arbitrari, ma tali che la loro congiungente incontri la retta c in un punto C. Si prendono poi sulla rette r, da bande opposte rispetto ad α, due punti P e Q, in modo che sia OP = OQ e si congiungono i punti P e Q con A, B e C.
Ricordando che l'asse di un segmento è il luogo dei punti equidistanti dagli estremi del segmento, nel piano PAQ risulta PA = OQ, essendo OA l'asse del segmento PQ, in quanto è perpendicolare a PQ nel suo punto medio; e nel piano PQB risulta PB = BQ, essendo OB l'asse del segmento BQ..
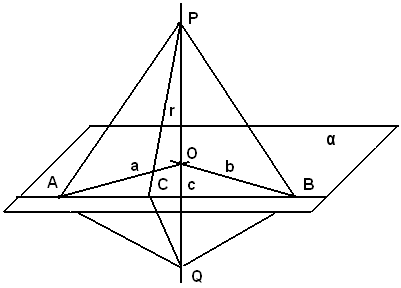
I triangoli PAB e QAB sono dunque uguali, perchè hanno i tre lati uguali, e precisamente PA = AQ, PB =BQ, AB in comune; di conseguenza gli angoli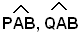
sono uguali.
Si considerano ora i due triangoli ACP e ACQ, essi risultano uguali perchè hanno uguali i lati AP e AQ, AC in comune ed uguale l'angolo compreso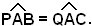
E' quindi PC = CQ e il triangolo PCQ risulta dunque isoscele sulla base PQ. E ciò dimostra che OC è l'asse del segmento PQ. Quindi la OC, ossia la retta c è perpendicolare a PQ, ovvero alla retta r. Il teorema è quindi dimostrato.
Corollario - Il luogo delle rette perpendicolari ad una retta data in un suo punto è il piano perpendicolare alla retta in quel punto.
Infatti, le rette del piano α perpendicolari ad una retta r in un suo punto A sono tutte perpendicolari alla r. Viceversa, qualsiasi retta AB perpendicolare alla r deve giacere nel piano α, perchè se giacesse al di fuori di α, il piano β=rAB intersecherebbe α lungo una retta AC passante per A e quindi tanto AB, quanto AC, pur giacendo nello stesso piano β, sarebbero perpendicolari ad r nello stesso punto A, e ciò è assurdo.
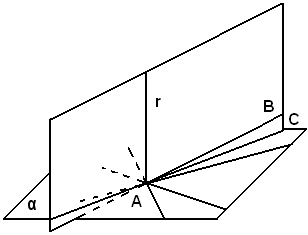
Teorema delle tre perpendicolari - Se una retta è perpendicolare ad un piano e dal suo piede si conduce la perpendicolare ad una retta qualsiasi del piano, quest'ultima è perpendicolare al piano delle prime due.
La retta AB sia perpendicolare al piano α e sia B il suo piede; si conduca da B la perpendicolare BC alla retta r di α.
Si deve dimostrare che la retta r è perpendicolare al piano formaro da AB e BC.
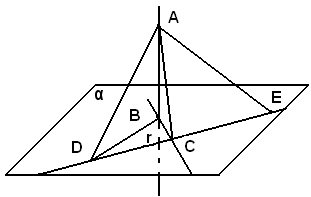
Infatti, sulla retta r, a partire dal punto C, da bande opposte ad esso, si costruiscono due segmenti CD e CE uguali e si congiungono E e D con B e con A. Si ha BD = BE, perchè nel piano α, BC è l'asse del segmento DE. I due triangoli ABD e ABE risultano allora uguali, perchè hanno AB in comune, BD = BE per dimostrazione e gli angoli
retti, perchè AB è perpendicolare ad α
per ipotesi. E' perciò AD = AE, e ciò prova che
nel piano ADE la retta AC è l'asse di DE, e quindi che AC
è perpendicolare a DE, ossia ad r.
Quest'ultima retta, essendo perpendicolare alle rette CB, AC, è perpendicolare al piano da esse formato, che è lo stesso di quello formato da AB e da BC.
Nota bene
Durante la dimostrazione si è implicitamente supposto che la retta r non passi per il piede B della perpendicolare AB ad α. In tale caso, la dimostrazione è immediata.
Infatti, se r passa per B, essa è perpendicolare alle rette AB e BC e quindi al loro piano.
Piano perpendicolare ad una retta per un punto
2)-il punto è esterno alla retta.
Sia r la retta e P un punto esterno ad essa.
Per P, nel piano Pr, si conduce la perpendicolare PA ad r e da A, fuori del piano Pr, un'altra retta AQ perpendicolare ad r. Il piano α delle rette PA e AQ è perpendicolare alla retta r perchè contiene due rette, PA e PQ, perpendicolari ad r.
Il piano per P perpendicolare ad r è unico.
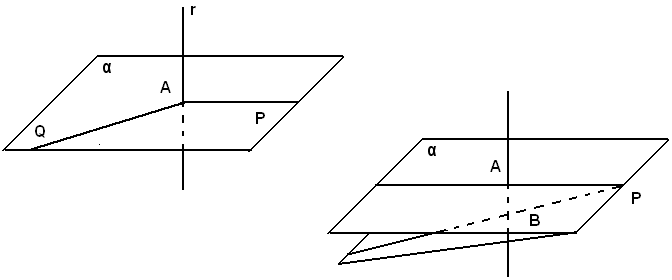
Anche in questo caso il piano per P perpendicolare alla retta r è unico; se ne esistessero ad esempio due, per P si potrebbero condurre due rette PA e PB entrambe perpendicolari alla stessa retta r, e ciò è assurdo.
Retta perpendicolare ad un piano per un punto
Teorema - Per un punto passa una ed una sola retta perpendicolare ad un piano dato.
Si distinguono due casi: o il punto appartiene al piano, o è esterno ad esso.
In ogni caso, si può procedere in unico modo, osservando le figure seguenti.
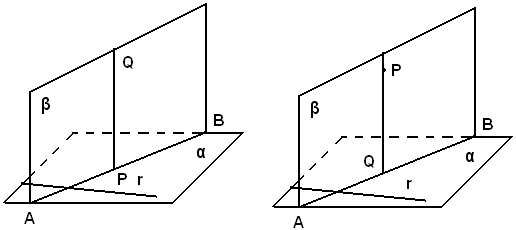
Si conduce nel piano α una retta r e da P il piano β perpendicolare ad r. Se AB è l'intersezione bi β con α, la perpendicolare PQ condotta da P ad AB è la perpendicolare richiesta.
Infatti, la perpendicolare PQ condotta da P alla retta AB è anche perpendicolare ad α, per il teorema delle tre perpendicolari, perchè essendo r perpendicolare ad AB ed AB perpendicolare a PQ, quest'ultima retta è perpendicolare al piano r, AB, ossia ad α.
La perpendicolare per un punto ad un piano è unica, altrimenti da un punto si potrebbero condurre più di una perpendicolare ad una stessa retta, la retta che congiungerebbe i piedi.
Piani perpendicolari
Si è visto che due piani che si tagliano dividono lo spazio in quattro parti dette diedri.
Se questi risultano uguali i piani che li formano si dicono perpendicolari.
Definizione - Due piani si dicono perpendicolari, se s'incontrano e formano quattro diedri uguali.
Teorema fondamentale sulla perpendicolarità fra piani
Se due piani sono perpendicolari, un terzo piano perpendicolare alla loro intersezione in un punto qualsiasi li taglia secondo rette perpendicolari. E viceversa.
Siano αα' e ββ' due piani perpendicolari che s'intersecano lungo una retta r e un terzo piano perpendicolare ad r in un punto O qualsiasi tagli il piano αα' lungo la retta AA' e il piano ββ' lungo la retta BB'.
Si deve dimostrare che le rette AA' e BB' sono perpendicolari.
Facendo ruotare tutta la figura di un quarto di giro intorno alla retta r, per l'uguaglianza dei quattro diedri, ogni diedro si sovrapporrà al successivo e quindi anche a ciascuno degli angoli formati dalle rette AA' e BB' si sovrapporrà al successivo. Ciò dimostra che i quattro angoli formati dalle rette AA' e BB' sono uguali e quindi che le stesse rette sono perpendicolari.
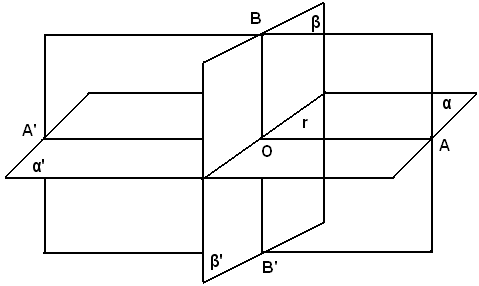
Viceversa, se le rette AA' e BB' sono perpendicolari, una rotazione di tutta la figura di un quarto di giro intorno alla retta r, farà sovrapporre ognuno degli angoli formati dalle due rette al successivo; quindi anche ognuno dei quattro diedri individuati dai due piani si sovrapporrà al successivo. Pertanto, i quattro diedri risultano uguali.
Teorema - Se due piani sono perpendicolari, la perpendicolare abbassata da un punto di uno di essi all'intersezione comune è perpendicolare all'altro piano.
Siano α e β i piani perpendicolari dati e r la loro intersezione.
Si deve dimostrare che la perpendicolare AB, condotta da un punto A del piano α ad r, è anche perpendicolare a β.
Basta dimostrare che a=AB è perpendicolare a due rette di β passanti per il piede B di AB.
Infatti, si conduce per il punto A il piano γ perpendicolare all'intersezione r di α e β.
Siccome questi piani sono perpendicolari per ipotesi, il piano γ li taglierà secondo rette perpendicolari, e precisamente taglierà α lungo la retta a e il piano β lungo una retta b. Ma allora la retta a è perpendicolare oltre che ad r, per ipotesi, anche alla retta b del piano β; essendo perciò perpendicolare alle due rette b ed r di β, sarà perpendicolare anche a β.
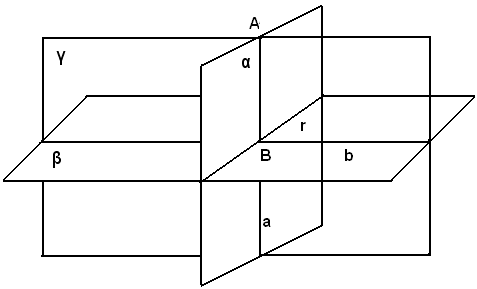
Corollario - Se due piani sono perpendicolari, le perpendicolari abbassate dai punti di uno di essi all'altro piano giacciono sul primo.
Infatti, come si nota dalla figura precedente, se i piani α e β sono perpendicolari, la perpendicolare AB abbassata da un punto di α all'intesezione r di α e β, giace su α. E questa è l'unica perpendicolare che si può condurre dal punto A al piano β.
Dati un piano e una retta:
1)-se la retta è perpendicolare al piano, tutti i piani passanti per la retta sono perpendicolare al piano;
2)-se la retta non è perpendicolare al piano, per essa passa uno ed un solo piano perpendicolare a quello dato.
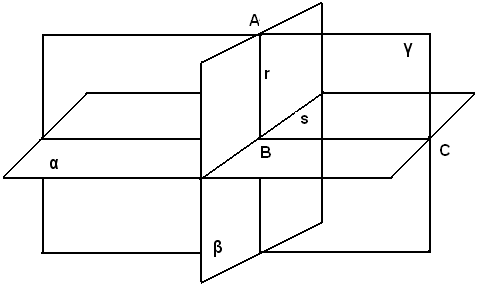
1)-Sia data la retta r perpendicolare al piano α.
Si deve dimostrare che qualsiasi piano β passante per r è perpendicolare al piano α.
Infatti, sia B il piede della perpendicolare r ad α. I due piani α e β, avendo il punto B in comune, avranno anche in comune una retta s passante per B.
Basta dimostrare che un piano γ passante per B e perpendicolare ad s taglia α e β secondo rette perpendicolari. Ora il piano γ taglia β lungo la retta r e α lungo una retta BC; e poichè r è perpendicolare ad α per ipotesi, risulta perpendicolare anche a BC. Quindi il piano γ taglia i piani α e β secondo le rette perpendicolari r e BC. Dunque, α e β sono perpendicolari.
2)-Si suppone che la retta r non è perpendicolare al piano α, giaccia o no sul piano α.
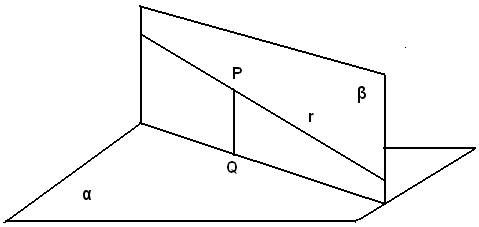
Si abbassa da un punto P di r la perpendicolare PQ al piano α. Il piano rPQ, passante per r è perpendicolare al piano α. Per P non può passare alcun altro piano perpendicolare ad α, poichè se esistesse, conducendo per il punto P la perpendicolare alla sua intersezione con il piano α, essa sarebbe perpendicolare ad α, per il teorema precedente, ed allora per un punto P si potrebbe condurre oltre la PQ, un'altra perpendicolare al piano α, il che è assurdo per un teorema precedente.
Proiezioni e distanze
Definizione - Si chiama proiezione di un punto su un piano il piede della perpendicolare condotta da quel punto al piano.
Definizione - Si chiama proiezione di una retta su un piano, al quale non sia perpendicolare, l'intersezione del piano con quello perpendicolare condotto per la retta.
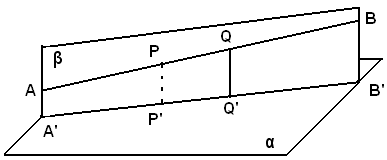
Definizione - Si chiama proiezione di un segmento su un piano, al quale non sia perpendicolare, il segmento che ha per estremi le proiezioni degli estremi.
Se una retta o un segmento sono perpendicolari ad un piano, la loro proiezione su questo è un punto.
Nella figura suddetta la retta A'B' è la proiezione della retta AB sul piano α. Il segmento P'Q' è la proiezione del segmento PQ sullo stesso piano α.
Definizione - Si chiama perpendicolare da un punto ad un piano il segmento di perpendicolare condotto dal punto al piano.
Definizione - Si chiama obliqua il segmento che congiunge un punto fuori dal piano con un punto del piano distinto dalla proiezione del punto sul piano.
Teorema - Dati un piano ed un punto fuori di esso, fra gli infiniti segmenti che congiungono il punto dato con i punti del piano:
1)-la perpendicolare è minore di ogni obliqua;
2)-due oblique aventi sul piano proiezioni uguali, sono uguali, e viceversa;
3)-due oblique aventi sul piano proiezioni disuguali, sono disuguali e precisamente è maggiore quella che ha la proiezione maggiore. E viceversa.
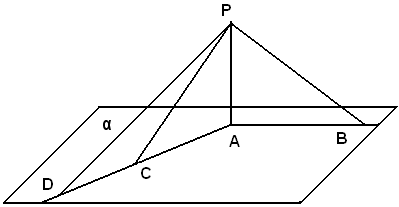
Sia α un piano, P un punto fuori di esso, PA la perpendicolare abbassata da P ad α.
1)-Se PB è un'obliqua, il triangolo PAB è rettangolo in A; segue che il cateto AP è minore dell'ipotenusa PB.
2)-Siano PB e PC due oblique e le loro proiezioni sul piano α, AB e AC siano uguali.
Si deve dimostrare che PB = PC.
Infatti, i due triangoli rettangoli PAB e PAC hanno il cateto AP in comune e i due cateti AB e AC uguali per ipotesi; sono quindi uguali e risulta PB = PC.
3)-Siano PB e PD due oblique e le loro intersezioni sul piano α, AB e AD, siano disuguali e precisamente AD>AB.
Si deve dimostrare che PD>PB.
Infatti, preso su AD un segmento AC = AB, si ha, per il caso precedente, PC = PB; ma sul piano APD il segmento PD ha proiezione maggiore di PC, allora è PD>PC e quindi PD>PB.
Le dimostrazioni inverse seguono per esclusione.
Definizione di distanza di un punto dal piano
Dato un piano e un punto fuori di esso, si chiama distanza di un punto dal piano, il segmento perpendicolare condotto dal punto al piano.
Simmetria e uguaglianza inversa
Definizione - Due punti si dicono simmetrici rispetto ad un piano, se il segmento che li congiunge è perpendicolare al piano ed è diviso da questo per metà.
Due figure si dicono simmetriche rispetto ad un piano, quando i punti dell'una hanno per simmetrici i punti dell'altra.
Un punto del piano si considera come simmetrico di se stesso.
Figure simmetriche si dicono anche corrispondenti nella simmetria.
Si potrebbe dimostrare, e ci si limita solo all'enunciato, che:
-nella simmetria rispetto ad un piano, ad una retta corrisponde una retta, ad una semiretta una semiretta, ad un segmento un segmento uguale. Inoltre ad un piano corrisponde un piano, ad un semipiano un semipiano, ad un angolo un angolo uguale, ad un poligono un poligono uguale, ad un diedro un diedro uguale.
Le proprietà precedenti valgono anche per figure uguali e ciò potrebbe far supporre che due figure simmetriche rispetto ad un piano siano uguali, cioè che l'una sia trasformabile nell'altra mediante un movimento. Ciò non è vero in generale.
Basta pensare, ad esempio, che l'immagine della mano destra nello specchio, che è la simmetrica rispetto al piano dello specchio, è uguale alla mano sinistra, e questa non è uguale, cioè sovrapponibile, alla destra. Questa osservazione intuitiva giustifica la seguente proposizione:
-due figure simmetriche rispetto ad un piano non sono in generale uguali.
Definizione - Due figure non sovrapponibili, tali che l'una sia uguale alla simmetrica dell'altra rispetto ad un piano si dicono inversamente uguali. Due figure sovrapponibili, si dicono invece direttamente uguali o uguali.
Finora sono state trattate le figure piane, ora si passa allo studio delle figure solide, ossia quelle in cui i punti non sono tutti contenuti nello stesso piano.
Ai postulati di appartenenza e al postulato della partizione del piano, si aggiunge il seguente postulato.
Postulato della partizione dello spazio
Ogni piano α divide lo spazio in due parti chiamate semispazi, tali che il segmento che congiunge due punti dello stesso semispazio non ha punti in comune con il piano α, mentre il segmento che congiunge due punti di semispazi diversi ha un punto in comune.
ll piano α si chiama contorno e i punti si considerano come appartenenti all'uno o all'altro semispazio.
Due punti si dicono dalla stessa banda o da bande opposte in un piano α a seconda che giacciono o no in uno solo dei semispazi individuati da α.
Si ha subito che:
semirette e semipiani, aventi l'origine sul contorno di un semipiano e passanti per un punto interno a questo, hanno tutti i punti interni al semispazio.
Nella figura suddetta risulta che:
-A e B stanno da una stessa parte,
-C e D stanno da parti opposte rispetto al piano α,
-la semiretta EF, con l'origine E sul piano α, sta da una stessa parte rispetto ad α.
Teorema - Se due piani hanno un punto in comune, hanno in comune una retta che passa per quel punto.
Siano α e β due piani aventi in comune il punto P.
Si deve dimostrare che α e β hanno in comune una retta passante per P.
Infatti, due rette distinte a e b, giacenti nel piano α e passanti per P, sono divise da P in semirette giacenti da bande opposte rispetto a β. Pertanto, sulle rette a e b si possono prendere rispettivamente due punti A e B da bande opposte a β; la congiungente AB interseca β in un punto Q, che è distinto da P; diversamente i punti A, P e B apparterrebbero alla stessa retta, e quindi a e b coinciderebbero. Perciò il punto Q appartiene al piano α, perchè la retta AB giace su α e appartiene al piano perchè β perchè AB interseca β. La retta PQ, avendo i suoi punti situati tanto su α quanto su β, appartiene ad entrambi i piani. Questi non possono avere alcuna retta in comune, altrimenti coinciderebbero.
Se due piani hanno una retta in comune, si dice che si tagliano o si segano lungo quella retta, la quale si chiama intersezione dei due piani.
Definizione - Due piani che si segano lungo una retta dividono lo spazio in quattro parti, ognuna delle quali si chiama angolo diedro o semplicemente diedro.
Il diedro si può considerare come costituito dall'insieme dei punti comuni a due semispazi i cui contorni s'incontrano lungo la retta.
Secondo la definizione generale di uguaglianza delle figure, due diedri sono uguali quando è possibile farli coincidere punto per punto.
Dai postulati fondamentali si deducono le seguenti mutue posizioni fra rette e piani:
1)-rette e piani - Dati una una retta e un piano nello spazio, si ha che:
a)-o la retta ha due punti distinti in comune con il piano, e allora tutta la retta giace nel piano;
b)-o ha un solo punto in comune, interseca il piano, ed è divisa dallo stesso in due semirette che giacciono nei semispazi opposti che hanno per contorno il piano;
c)-o non ha nessun punto in comune con il piano, e si vedrà in seguito che ciò è possibile, e si dirà che la retta è parallela al piano;
2)-piani - Due piani nello spazio:
a)-o hanno tre punti in comune, non in linea retta, e coincidono;
b)-o hanno due o un solo punto in comune e hanno in comune una retta che passa per quei punti e si dicono incidenti o secanti;
c)-o non hanno nessun punto in comune, e si vedrà in seguito che ciò è possibile, e si dirà che i due piani sono paralleli;
3)-rette - Due rette nello spazio:
a)-o hanno due punti in comune e allora coincidono;
b)-o hanno un solo punto in comune;
c)-o non hanno nessun punto in comune, e in tal caso giacciono in uno stesso piano e sono parallele, o non giacciono in uno stesso piano e si dicono sghembe.
Sono sghembe, ad esempio, due rette di cui una giace in un piano α e l'altra interseca il piano in un punto fuori dalla retta, come a e b nella figura seguente.
Rette e piani perpendicolari
Definizione - Una retta e un piano si dicono perpendicolari quando la retta incontra il piano ed è perpendicolare a tutte le rette del piano passanti per il punto di intersezione. Questo punto si chiama piede della perpendicolare.
Teorema fondamentale sulla perpendicolarità - Se una retta è perpendicolare a due rette di un piano, passanti per la sua intersezione con il piano, è anche perpendicolare a tutte le altre rette del piano che passano per la stessa intersezione e quindi è perpendicolare al piano.
Una retta r incontri il piano α in un punto O e risulti perpendicolare alle due rette a e b che appartengono ad α.
Si deve dimostrare che la retta r è perpendicolare a qualsiasi retta c uscente da O e giacente nel piano α.
Infatti, sulle rette a e b si prendono rispettivamente i punti A, e B arbitrari, ma tali che la loro congiungente incontri la retta c in un punto C. Si prendono poi sulla rette r, da bande opposte rispetto ad α, due punti P e Q, in modo che sia OP = OQ e si congiungono i punti P e Q con A, B e C.
Ricordando che l'asse di un segmento è il luogo dei punti equidistanti dagli estremi del segmento, nel piano PAQ risulta PA = OQ, essendo OA l'asse del segmento PQ, in quanto è perpendicolare a PQ nel suo punto medio; e nel piano PQB risulta PB = BQ, essendo OB l'asse del segmento BQ..
I triangoli PAB e QAB sono dunque uguali, perchè hanno i tre lati uguali, e precisamente PA = AQ, PB =BQ, AB in comune; di conseguenza gli angoli
sono uguali.Si considerano ora i due triangoli ACP e ACQ, essi risultano uguali perchè hanno uguali i lati AP e AQ, AC in comune ed uguale l'angolo compreso
E' quindi PC = CQ e il triangolo PCQ risulta dunque isoscele sulla base PQ. E ciò dimostra che OC è l'asse del segmento PQ. Quindi la OC, ossia la retta c è perpendicolare a PQ, ovvero alla retta r. Il teorema è quindi dimostrato.
Corollario - Il luogo delle rette perpendicolari ad una retta data in un suo punto è il piano perpendicolare alla retta in quel punto.
Infatti, le rette del piano α perpendicolari ad una retta r in un suo punto A sono tutte perpendicolari alla r. Viceversa, qualsiasi retta AB perpendicolare alla r deve giacere nel piano α, perchè se giacesse al di fuori di α, il piano β=rAB intersecherebbe α lungo una retta AC passante per A e quindi tanto AB, quanto AC, pur giacendo nello stesso piano β, sarebbero perpendicolari ad r nello stesso punto A, e ciò è assurdo.
Teorema delle tre perpendicolari - Se una retta è perpendicolare ad un piano e dal suo piede si conduce la perpendicolare ad una retta qualsiasi del piano, quest'ultima è perpendicolare al piano delle prime due.
La retta AB sia perpendicolare al piano α e sia B il suo piede; si conduca da B la perpendicolare BC alla retta r di α.
Si deve dimostrare che la retta r è perpendicolare al piano formaro da AB e BC.
Infatti, sulla retta r, a partire dal punto C, da bande opposte ad esso, si costruiscono due segmenti CD e CE uguali e si congiungono E e D con B e con A. Si ha BD = BE, perchè nel piano α, BC è l'asse del segmento DE. I due triangoli ABD e ABE risultano allora uguali, perchè hanno AB in comune, BD = BE per dimostrazione e gli angoli
retti, perchè AB è perpendicolare ad α
per ipotesi. E' perciò AD = AE, e ciò prova che
nel piano ADE la retta AC è l'asse di DE, e quindi che AC
è perpendicolare a DE, ossia ad r.Quest'ultima retta, essendo perpendicolare alle rette CB, AC, è perpendicolare al piano da esse formato, che è lo stesso di quello formato da AB e da BC.
Nota bene
Durante la dimostrazione si è implicitamente supposto che la retta r non passi per il piede B della perpendicolare AB ad α. In tale caso, la dimostrazione è immediata.
Infatti, se r passa per B, essa è perpendicolare alle rette AB e BC e quindi al loro piano.
Piano perpendicolare ad una retta per un punto
Teorema - Per un punto passa uno ed un solo piano perpendicolare ad una retta data.
Si distinguono due casi: o il punto appartiene alla retta o è esterno ad essa.
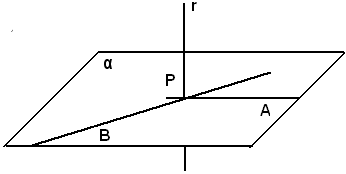
1)-il punto appartiene alla retta.
Sia r la retta e P un suo punto.
Si deve dimostrare che per P passa un solo piano perpendicolare alla retta data.
Si conducono per P due perpendicolari distinte PA e PB alla retta r; il piano α da esse formato risulta perpendicolare alla retta r, per il teorema sulla perpendicolarità fra retta e piano. Esso è unico, perchè le perpendicolari ad r in P giacciono tutte in uno stesso piano, come già visto.
Si distinguono due casi: o il punto appartiene alla retta o è esterno ad essa.
1)-il punto appartiene alla retta.
Sia r la retta e P un suo punto.
Si deve dimostrare che per P passa un solo piano perpendicolare alla retta data.
Si conducono per P due perpendicolari distinte PA e PB alla retta r; il piano α da esse formato risulta perpendicolare alla retta r, per il teorema sulla perpendicolarità fra retta e piano. Esso è unico, perchè le perpendicolari ad r in P giacciono tutte in uno stesso piano, come già visto.
2)-il punto è esterno alla retta.
Sia r la retta e P un punto esterno ad essa.
Per P, nel piano Pr, si conduce la perpendicolare PA ad r e da A, fuori del piano Pr, un'altra retta AQ perpendicolare ad r. Il piano α delle rette PA e AQ è perpendicolare alla retta r perchè contiene due rette, PA e PQ, perpendicolari ad r.
Il piano per P perpendicolare ad r è unico.
Anche in questo caso il piano per P perpendicolare alla retta r è unico; se ne esistessero ad esempio due, per P si potrebbero condurre due rette PA e PB entrambe perpendicolari alla stessa retta r, e ciò è assurdo.
Retta perpendicolare ad un piano per un punto
Teorema - Per un punto passa una ed una sola retta perpendicolare ad un piano dato.
Si distinguono due casi: o il punto appartiene al piano, o è esterno ad esso.
In ogni caso, si può procedere in unico modo, osservando le figure seguenti.
Si conduce nel piano α una retta r e da P il piano β perpendicolare ad r. Se AB è l'intersezione bi β con α, la perpendicolare PQ condotta da P ad AB è la perpendicolare richiesta.
Infatti, la perpendicolare PQ condotta da P alla retta AB è anche perpendicolare ad α, per il teorema delle tre perpendicolari, perchè essendo r perpendicolare ad AB ed AB perpendicolare a PQ, quest'ultima retta è perpendicolare al piano r, AB, ossia ad α.
La perpendicolare per un punto ad un piano è unica, altrimenti da un punto si potrebbero condurre più di una perpendicolare ad una stessa retta, la retta che congiungerebbe i piedi.
Piani perpendicolari
Si è visto che due piani che si tagliano dividono lo spazio in quattro parti dette diedri.
Se questi risultano uguali i piani che li formano si dicono perpendicolari.
Definizione - Due piani si dicono perpendicolari, se s'incontrano e formano quattro diedri uguali.
Teorema fondamentale sulla perpendicolarità fra piani
Se due piani sono perpendicolari, un terzo piano perpendicolare alla loro intersezione in un punto qualsiasi li taglia secondo rette perpendicolari. E viceversa.
Siano αα' e ββ' due piani perpendicolari che s'intersecano lungo una retta r e un terzo piano perpendicolare ad r in un punto O qualsiasi tagli il piano αα' lungo la retta AA' e il piano ββ' lungo la retta BB'.
Si deve dimostrare che le rette AA' e BB' sono perpendicolari.
Facendo ruotare tutta la figura di un quarto di giro intorno alla retta r, per l'uguaglianza dei quattro diedri, ogni diedro si sovrapporrà al successivo e quindi anche a ciascuno degli angoli formati dalle rette AA' e BB' si sovrapporrà al successivo. Ciò dimostra che i quattro angoli formati dalle rette AA' e BB' sono uguali e quindi che le stesse rette sono perpendicolari.
Viceversa, se le rette AA' e BB' sono perpendicolari, una rotazione di tutta la figura di un quarto di giro intorno alla retta r, farà sovrapporre ognuno degli angoli formati dalle due rette al successivo; quindi anche ognuno dei quattro diedri individuati dai due piani si sovrapporrà al successivo. Pertanto, i quattro diedri risultano uguali.
Teorema - Se due piani sono perpendicolari, la perpendicolare abbassata da un punto di uno di essi all'intersezione comune è perpendicolare all'altro piano.
Siano α e β i piani perpendicolari dati e r la loro intersezione.
Si deve dimostrare che la perpendicolare AB, condotta da un punto A del piano α ad r, è anche perpendicolare a β.
Basta dimostrare che a=AB è perpendicolare a due rette di β passanti per il piede B di AB.
Infatti, si conduce per il punto A il piano γ perpendicolare all'intersezione r di α e β.
Siccome questi piani sono perpendicolari per ipotesi, il piano γ li taglierà secondo rette perpendicolari, e precisamente taglierà α lungo la retta a e il piano β lungo una retta b. Ma allora la retta a è perpendicolare oltre che ad r, per ipotesi, anche alla retta b del piano β; essendo perciò perpendicolare alle due rette b ed r di β, sarà perpendicolare anche a β.
Corollario - Se due piani sono perpendicolari, le perpendicolari abbassate dai punti di uno di essi all'altro piano giacciono sul primo.
Infatti, come si nota dalla figura precedente, se i piani α e β sono perpendicolari, la perpendicolare AB abbassata da un punto di α all'intesezione r di α e β, giace su α. E questa è l'unica perpendicolare che si può condurre dal punto A al piano β.
Dati un piano e una retta:
1)-se la retta è perpendicolare al piano, tutti i piani passanti per la retta sono perpendicolare al piano;
2)-se la retta non è perpendicolare al piano, per essa passa uno ed un solo piano perpendicolare a quello dato.
1)-Sia data la retta r perpendicolare al piano α.
Si deve dimostrare che qualsiasi piano β passante per r è perpendicolare al piano α.
Infatti, sia B il piede della perpendicolare r ad α. I due piani α e β, avendo il punto B in comune, avranno anche in comune una retta s passante per B.
Basta dimostrare che un piano γ passante per B e perpendicolare ad s taglia α e β secondo rette perpendicolari. Ora il piano γ taglia β lungo la retta r e α lungo una retta BC; e poichè r è perpendicolare ad α per ipotesi, risulta perpendicolare anche a BC. Quindi il piano γ taglia i piani α e β secondo le rette perpendicolari r e BC. Dunque, α e β sono perpendicolari.
2)-Si suppone che la retta r non è perpendicolare al piano α, giaccia o no sul piano α.
Si abbassa da un punto P di r la perpendicolare PQ al piano α. Il piano rPQ, passante per r è perpendicolare al piano α. Per P non può passare alcun altro piano perpendicolare ad α, poichè se esistesse, conducendo per il punto P la perpendicolare alla sua intersezione con il piano α, essa sarebbe perpendicolare ad α, per il teorema precedente, ed allora per un punto P si potrebbe condurre oltre la PQ, un'altra perpendicolare al piano α, il che è assurdo per un teorema precedente.
Proiezioni e distanze
Definizione - Si chiama proiezione di un punto su un piano il piede della perpendicolare condotta da quel punto al piano.
Definizione - Si chiama proiezione di una retta su un piano, al quale non sia perpendicolare, l'intersezione del piano con quello perpendicolare condotto per la retta.
Definizione - Si chiama proiezione di un segmento su un piano, al quale non sia perpendicolare, il segmento che ha per estremi le proiezioni degli estremi.
Se una retta o un segmento sono perpendicolari ad un piano, la loro proiezione su questo è un punto.
Nella figura suddetta la retta A'B' è la proiezione della retta AB sul piano α. Il segmento P'Q' è la proiezione del segmento PQ sullo stesso piano α.
Definizione - Si chiama perpendicolare da un punto ad un piano il segmento di perpendicolare condotto dal punto al piano.
Definizione - Si chiama obliqua il segmento che congiunge un punto fuori dal piano con un punto del piano distinto dalla proiezione del punto sul piano.
Teorema - Dati un piano ed un punto fuori di esso, fra gli infiniti segmenti che congiungono il punto dato con i punti del piano:
1)-la perpendicolare è minore di ogni obliqua;
2)-due oblique aventi sul piano proiezioni uguali, sono uguali, e viceversa;
3)-due oblique aventi sul piano proiezioni disuguali, sono disuguali e precisamente è maggiore quella che ha la proiezione maggiore. E viceversa.
Sia α un piano, P un punto fuori di esso, PA la perpendicolare abbassata da P ad α.
1)-Se PB è un'obliqua, il triangolo PAB è rettangolo in A; segue che il cateto AP è minore dell'ipotenusa PB.
2)-Siano PB e PC due oblique e le loro proiezioni sul piano α, AB e AC siano uguali.
Si deve dimostrare che PB = PC.
Infatti, i due triangoli rettangoli PAB e PAC hanno il cateto AP in comune e i due cateti AB e AC uguali per ipotesi; sono quindi uguali e risulta PB = PC.
3)-Siano PB e PD due oblique e le loro intersezioni sul piano α, AB e AD, siano disuguali e precisamente AD>AB.
Si deve dimostrare che PD>PB.
Infatti, preso su AD un segmento AC = AB, si ha, per il caso precedente, PC = PB; ma sul piano APD il segmento PD ha proiezione maggiore di PC, allora è PD>PC e quindi PD>PB.
Le dimostrazioni inverse seguono per esclusione.
Definizione di distanza di un punto dal piano
Dato un piano e un punto fuori di esso, si chiama distanza di un punto dal piano, il segmento perpendicolare condotto dal punto al piano.
Simmetria e uguaglianza inversa
Definizione - Due punti si dicono simmetrici rispetto ad un piano, se il segmento che li congiunge è perpendicolare al piano ed è diviso da questo per metà.
Due figure si dicono simmetriche rispetto ad un piano, quando i punti dell'una hanno per simmetrici i punti dell'altra.
Un punto del piano si considera come simmetrico di se stesso.
Figure simmetriche si dicono anche corrispondenti nella simmetria.
Si potrebbe dimostrare, e ci si limita solo all'enunciato, che:
-nella simmetria rispetto ad un piano, ad una retta corrisponde una retta, ad una semiretta una semiretta, ad un segmento un segmento uguale. Inoltre ad un piano corrisponde un piano, ad un semipiano un semipiano, ad un angolo un angolo uguale, ad un poligono un poligono uguale, ad un diedro un diedro uguale.
Le proprietà precedenti valgono anche per figure uguali e ciò potrebbe far supporre che due figure simmetriche rispetto ad un piano siano uguali, cioè che l'una sia trasformabile nell'altra mediante un movimento. Ciò non è vero in generale.
Basta pensare, ad esempio, che l'immagine della mano destra nello specchio, che è la simmetrica rispetto al piano dello specchio, è uguale alla mano sinistra, e questa non è uguale, cioè sovrapponibile, alla destra. Questa osservazione intuitiva giustifica la seguente proposizione:
-due figure simmetriche rispetto ad un piano non sono in generale uguali.
Definizione - Due figure non sovrapponibili, tali che l'una sia uguale alla simmetrica dell'altra rispetto ad un piano si dicono inversamente uguali. Due figure sovrapponibili, si dicono invece direttamente uguali o uguali.