MIKY & GENNY
CASI PARTICOLARI DI RISOLUZIONE DEI TRIANGOLI ---> INDICE
Mediante
le formule stabilite si può risolvere un triangolo conoscendo, oltre ai lati o gli angoli, altri elementi.
1° caso
-risoluzione di un triangolo, conoscendo due angoli e il perimetro.
Indicando con α e β i due angoli e con 2p il perimetro, intanto si ha:
γ = 180° - (α + β);
partendo dal teorema dei seni e applicando il componendo alla proporzione espressa dallo stesso, si può scrivere:
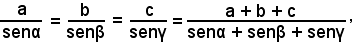
o anche, essendo
a + b + c = 2p,
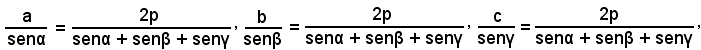
da cui
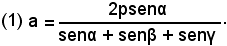
Per il calcolo dei lati b e c si procede allo stesso modo.
Le formule trovate si possono trasformare in altre idonee al calcolo logaritmico; mediante le formule di prostaferesi e di duplicazione si ottiene:
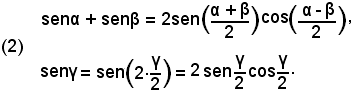
Inoltre, essendo
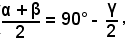
da cui
si ha:
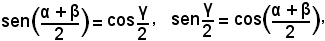
quindi, sostituendo nelle (2), risulta
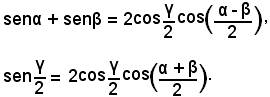
Sommando membro a membro, si ha:
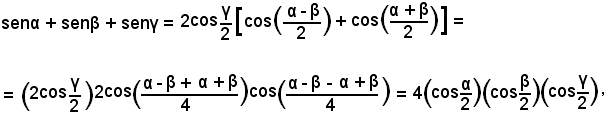
e sostituendo questo risultato nelle (1), segue che:
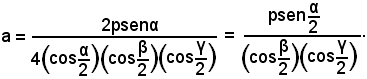
Per il calcolo dei lati b e c si allo stesso modo.
2° caso
-risoluzione di un triangolo, conoscendo due angoli e l'area.
Indicando con α e β i due angoli e con S l'area, intanto si ha:
γ = 180° - (α + β);
successivamente, mediante la formula che esprime l'area di un triangolo in funzione di un lato e dei due angoli adiacenti, cioè
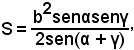
si ricava:
e quindi la formula
e le analoghe.
3° caso
-risoluzione di un triangolo, conoscendo due angoli ed un'altezza.
Indicando con α e β i due angoli e con hc l'altezza, intanto si ha:
γ = 180° - (α + β).
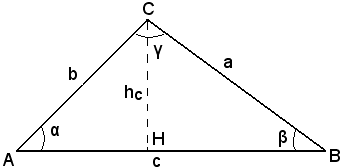
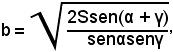
Inoltre, dai due triangoli rettangoli CAH, CBH, risulta:
hc = bsenα, hc = asenβ,
da cui
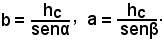
Per ottenere poi il terzo lato, si applica il teorema dei seni.
Infatti, da
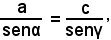
segue che
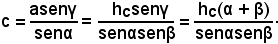
4° caso
-risoluzione di un triangolo, conoscendo due angoli e il raggio del cerchio circoscritto o inscritto.
Indicando con R il raggio del cerchio circoscritto e con α e β i due angoli, intanto si ha:
γ = 180° - (α + β).
Dal teorema dei seni risulta
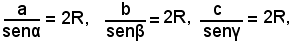
e si ottiene
a = 2Rsenα, b = 2Rsenβ, c = 2Rsenγ.
Se invece si considera il raggio r del cerchio inscritto, come in figura, risulta:
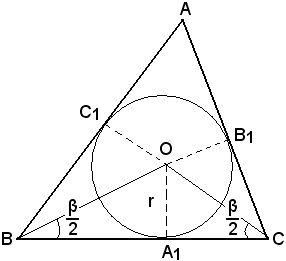
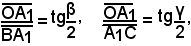
da cui
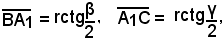
e quindi, sommando membro a membro, si ha
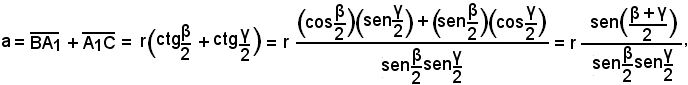
cioè
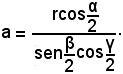
Formule analoghe si trovano per i lati b e c.
Altri casi interessanti di risoluzione si ottengono quando non si assegnano più elementi distinti di un triangolo, ma convenienti combinazioni. Anche su questo argomento ci si limita ad esporre alcuni tra i casi più caratteristici.
5° caso
-risoluzione di un triangolo, conoscendo un lato, l'angolo opposto e la somma o la differenza degli altri due lati.
Indicando con a il lato, con α l'angolo opposto e con s la somma degli altri due lati, cioè s = a + b, dalla formula seguente di Delambre:
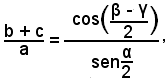
si ottiene
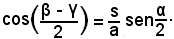
Mediante le tavole, si ricava il valore di
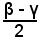
e quindi di β - γ.
Indicando tale valore con φ, si ottiene allora il sistema
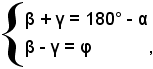
da cui, sommando e sottraendo, si deducono i valori
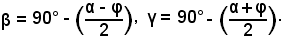
si ottiene
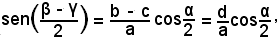
da cui si ricava il valore di
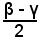
e quindi di β - γ.
Si procede poi come nel caso precedente.
Questo esempio di risoluzione dei triangoli si presta ad una semplice costruzione geometrica, supponendo di conoscere:
a)-il lato a, l'angolo α e la somma s = b + c degli altri due lati.
Si costruisce l'angolo
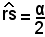
di vertice O e sul lato s si traccia un segmento
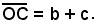
Successivamente si traccia la circonferenza di centro C e raggio a, che incontra l'altro lato r dell'angolo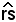
nei due punti B1, B2, supponendo che tali intersezioni esistano.
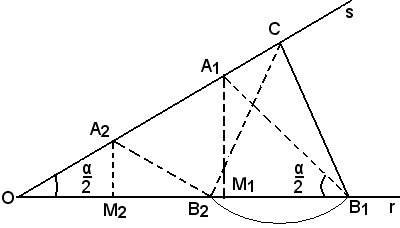
Indicati poi con M1, M2 i punti medi dei due segmenti OB1, OB2, si conducono da tali punti le perpendicolari ad r fino ad incontrare il lato s nei punti A1, A2, supponendo sempre che tali intersezioni esistano.
I due triangoli A1B1C, A2B2C soddisfano le condizioni date.
Infatti, si considera il triangolo A1B1C, nel quale il lato CB1 è per costruzione uguale ad a.
Poichè A1 è sull'asse del segmento OB1, risulta A1B1 = A1O e quindi:
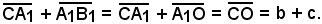
Inoltre,
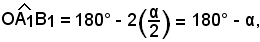
e perciò l'angolo
, come supplementare di 
, è uguale ad α, e ciò dimostra quanto asserito.
Per l'altro triangolo A2B2C il ragionamento è analogo.
Si suppone ora di conoscere:
b)-la differenza d = b - c.
Si costruisce l'angolo
di vertice O e sul lato s si riporta un segmento
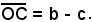
Successivamente si traccia la circonferenza di centro C e raggio a, che incontra l'altro lato r in un punto B.
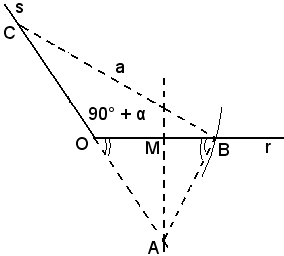
Detto M il punto medio del segmento OB, da questo si conduce la perpendicolare ad r fino ad incontrare il prolungamento di s in A. Il triangolo ABC così ottenuto è quello richiesto.
Infatti, il lato CB è uguale ad a per costruzione, inoltre essendo l'angolo
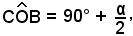
l'angolo
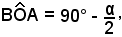
in quanto suo supplementare.
Inoltre il triangolo OBA è isoscele, perchè A appartiene all'asse di OB e quindi l'angolo al vertic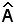e
è
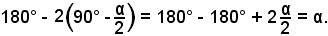
Infine risulta:
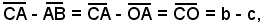
e ciò dimostra quanto asserito.
6° caso
-risoluzione di un triangolo, conoscendo un lato, un angolo ad esso adiacente e la somma o la differenza degli altri due.
Indicati con a il lato, con β l'angolo opposto e con s la somma degli altri due lati, cioè s = b + c, si parte dalla formule di Briggs relative alla tangente:
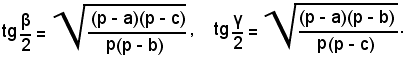
Moltiplicando membro a membro, si ottiene:
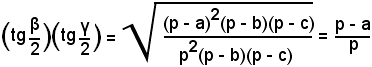
e quindi, sostituendo a p la sua espressione, risulta
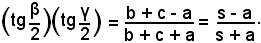
Segue che: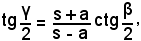
da cui, mediante le tavole, si ottiene γ/2 e quindi γ; di conseguenza α = 180° - (β + γ). Ottenuti i tre angoli, mediante il teorema dei seni, si trovano i lati b e c.
Si suppone ora di conoscere la differenza d = b - c; si parte ancora dalle formule di Briggs relative alla tangente e, dividendole membro a membro, si ha:
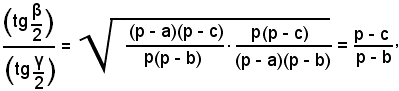
da cui
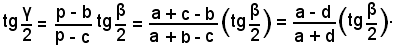
Mediante le tavole, da questa relazione si ottiene γ/2 e quindi γ; di conseguenza α = 180° - (β + γ). Ottenuti i tre angoli, mediante il teorema dei seni, si trovano i lati b e c.
Anche questi due modi di risoluzione si prestano ad una costruzione geometrica molto semplice:
a)-si costruisce un angolo
di vertice B.
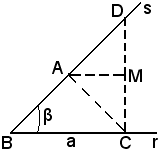
Si prende sul lato r il segmento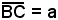
e su s il segmento 
.
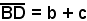Si congiunge poi C con D e, detto M il punto medio di CD, si conduce da M la perpendicolare alla CD fino ad incontrare s in A.
Si vuole dimostrare che il triangolo ABC così ottenuto soddisfa le condizioni date.
Infatti, tale triangolo ha il lato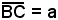 e l'angolo in 
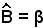, per costruzione; inoltre poichè A si trova sull'asse del segmento DC, risulta AC = DA, da cui,
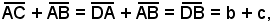
e ciò dimostra quanto asserito.
b)-Nel caso in cui si conosce la differenza b - c, si riporta sul prolungamento s' del lato s il segmento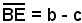
e sul lato r il segmento .
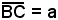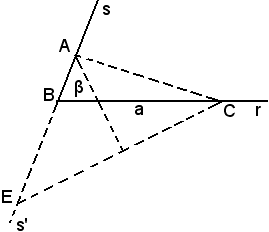
Congiunto E con C, si conduce l'asse del segmento EC, fino ad incontrare il lato s in A; il triangolo ABC soddisfa le condizioni date.
Infatti, tale triangolo ha il lato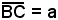, l'angolo 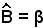, per costruzione, inoltre siccome A si trova sull'asse del segmento EC, risulta EA = AC, pertanto si ha:
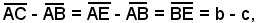
e ciò dimostra quanto asserito.
Nota bene
Queste costruzioni conservano naturalmente un loro preciso significato sotto l'ipotesi che effettivamente esistano i vari punti d'incontro di cui si parla. La ricerca delle condizioni, sotto le quali ciò avviene effettivamente, porterebbe alla determinazione di certe condizioni analitiche che rappresenterebbero il risultato della discussione. Tale ricerca si omette.
7° caso
-risoluzione di un triangolo, conoscendo i raggi dei cerchi ex-inscritti.
Indicando tali raggi con ra, rb, rc, dalle formule
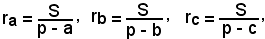
moltiplicandole a due a due, si ha:
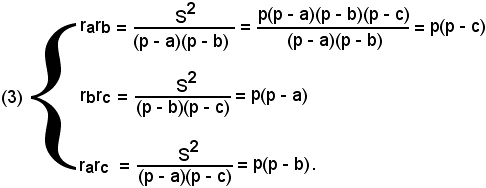
Sommando membro a membro, segue:
rarb + rbrc + rarc = p(p - c) + p(p - a) + p(p - b) = p[3p - (a + b + c)] = p(3p - 2p) = p2
e quindi
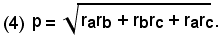
Inoltre, risolvendo la prima delle (3) rispetto a c, si ottiene:
rarb = p2 - pc,
da cui
e per la formula (4)
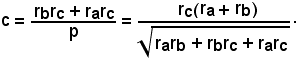
Per gli altri due lati a e b si procede analogamente.
Per ottenere gli angoli ci si serve delle formule di Briggs relative alle tangenti, si ha:
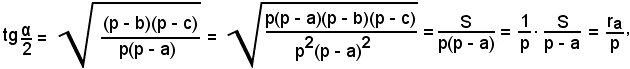
o anche
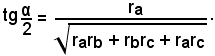
Si procede analogamente per:
Applicazioni della trigonometria negli altri campi
Moltissime applicazioni della trigonometria si trovano nella geodesia, nella topografia e nell'astronomia. Si accennano soltanto alcuni problemi semplici ed elementari, osservando che in questi campi le misure delle lunghezze e degli angoli, relative ai dati del problema in esame, vengono eseguite con metodi molto accurati, mediante strumenti di precisione, come livelli azimutali, teodoliti, tacheometri, stadie e cannocchiali anallattici.
Problema 1 - Calcolare l'altezza di una torre la cui cima sia inaccessibile.
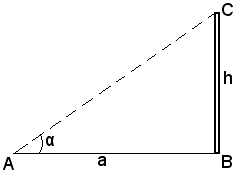
Sia h l'altezza della torre, schematizzata in figura con il segmento BC; si misuri orizzontalmente sul terreno, a partire dal piede B della torre, una distanza a piacere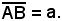
Si misuri poi l'angolo 
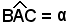e, dal triangolo rettangolo ABC, si ha:
h = atgα.
Se la distanza AB non è orizzontale, si indichi con H il punto in cui l'orizzontale per A incontra la vericale BC, come risulta dalle figure seguenti.
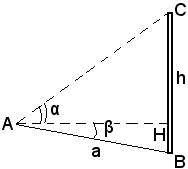
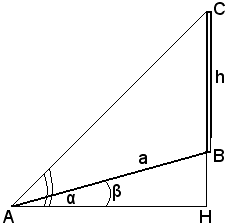
Si misurano allora da A gli angoli
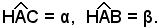
Applicando il teorema dei seni al triangolo ABC, segue che:
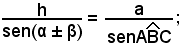
siccome
è complementare di α, risulta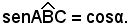 
Quindi:
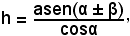
dove si considera il segno + o -, a seconda che B si trovi al di sotto o al di sopra dell'orizzontale AH.
Problema 2 - Calcolare la distanza di un punto da un altro visibile ma non accessibile.
Questo problema ha molta importanza in astronomia e in topografia, per il rilievo dei terreni.
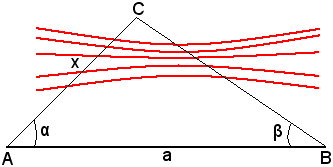
Si suppone che i due punti A e C, visibili l'uno dall'altro, siano separati da un ostacolo, per esempio da un fiume. Fissato un punto B, si misura la distanza qualsiasi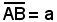
, e poi gli angoli
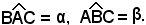
Detta x la distanza incognita AC, applicando il teorema dei seni al triangolo ABC, del quale si conoscono un lato e i due angoli adiacenti, risulta:
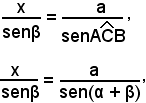
e quindi
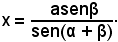
Problema 3 (Problema di Hansen o di Snellius) - Calcolare la distanza fra due punti visibili, ma non accessibili.
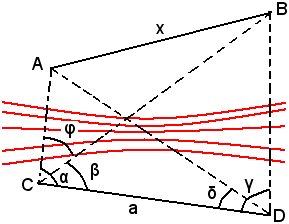
Siano A, B i punti visibili da C, ma non accessibili; si misura una base qualsiasi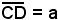
e poi i cinque angoli
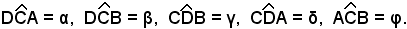
Se in particolare i punti A, B, C, D sono complanari, basta misurare solo gli angoli α, β, γ, δ, φ, perchè allora φ = α - β.
In ciascuno dei triangoli ACD, BCD si vengono così a conoscere un lato e due angoli, quindi si ha:
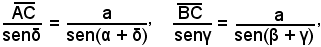
e si possono determinare i lati AC, BC.
Dal triangolo ABC infine, essendo noti i due lati AC, BC e l'angolo compreso φ, si trova la misura x del lato AB, ossia la distanza cercata.
Problema 4 (Problema di Pothenot o dei quattro punti).
Questo è il classico problema, molto importante in topografia.
Dati tre punti A, B, C, complanari, non allineati, e un quarto punto P, complanare con essi e posto internamente all'angolo convesso ABC, si tratta di calcolare le distanze di P dagli altri punti A, B, C.
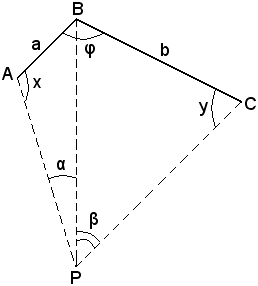
Sono noti gli angoli
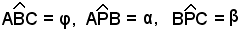
e i lati
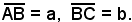
S'introducono ora due angoli ausiliari x, y, ponendo:
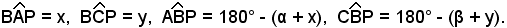
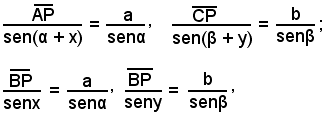
Applicando il teorema dei seni a ciascuno dei triangoli ABP, BCP e ricordando che angoli supplementari hanno seni uguali, segue che:
da cui
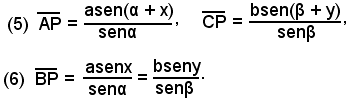
Da queste formule risulta evidente che, per trovare le distanze AP, BP, CP, occorre determinare gli angoli ausiliari x, y. Poichè la somma degli angoli interni di un quadrilatero è uguale a 360°, si ha:
x + y + α + β + φ = 360°,
quindi
x + y = 360° - (α + β + φ)
e si indica con ω.
Si calcola ora il valore della differenza x - y.
Dall'uguaglianza (6), si ha:
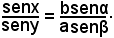
Allora si calcola l'angolo γ del I quadrante, tale che
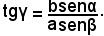
Quindi si ha:
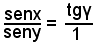
e perciò, per proprietà note delle proporzioni,
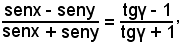
o anche, ricordando che tg45° = 1,
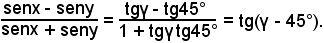
Per il teorema di Nepero, è noto che:
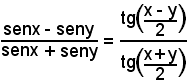
e si ha:
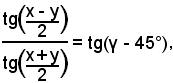
ossia
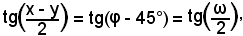
con ω noto.
Da questa relazione si ricava
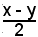
e poi x - y; ponendo x - y = ρ, si deduce il sistema
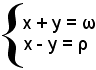
e si determinano facilmente gli angoli ausiliari x, y. Dopo di ciò, le distanze cercate sono date dalle formule (5) e (6).
1° caso
-risoluzione di un triangolo, conoscendo due angoli e il perimetro.
Indicando con α e β i due angoli e con 2p il perimetro, intanto si ha:
γ = 180° - (α + β);
partendo dal teorema dei seni e applicando il componendo alla proporzione espressa dallo stesso, si può scrivere:
o anche, essendo
a + b + c = 2p,
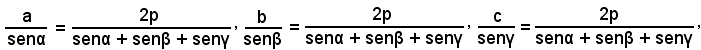
da cui
Per il calcolo dei lati b e c si procede allo stesso modo.
Le formule trovate si possono trasformare in altre idonee al calcolo logaritmico; mediante le formule di prostaferesi e di duplicazione si ottiene:
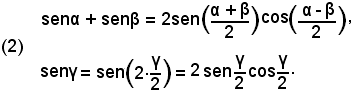
Inoltre, essendo
da cui
si ha:
quindi, sostituendo nelle (2), risulta
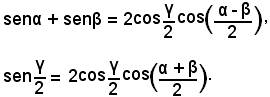
Sommando membro a membro, si ha:
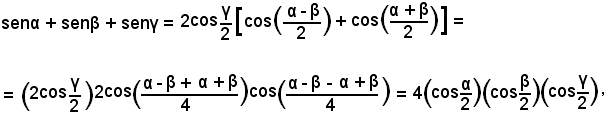
e sostituendo questo risultato nelle (1), segue che:
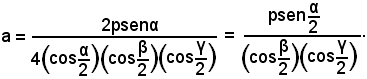
Per il calcolo dei lati b e c si allo stesso modo.
2° caso
-risoluzione di un triangolo, conoscendo due angoli e l'area.
Indicando con α e β i due angoli e con S l'area, intanto si ha:
γ = 180° - (α + β);
successivamente, mediante la formula che esprime l'area di un triangolo in funzione di un lato e dei due angoli adiacenti, cioè
si ricava:
e quindi la formula
e le analoghe.
3° caso
-risoluzione di un triangolo, conoscendo due angoli ed un'altezza.
Indicando con α e β i due angoli e con hc l'altezza, intanto si ha:
hc = bsenα, hc = asenβ,
da cui
Per ottenere poi il terzo lato, si applica il teorema dei seni.
Infatti, da
segue che
4° caso
-risoluzione di un triangolo, conoscendo due angoli e il raggio del cerchio circoscritto o inscritto.
Indicando con R il raggio del cerchio circoscritto e con α e β i due angoli, intanto si ha:
Dal teorema dei seni risulta
e si ottiene
Se invece si considera il raggio r del cerchio inscritto, come in figura, risulta:
da cui
e quindi, sommando membro a membro, si ha
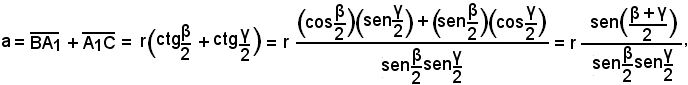
cioè
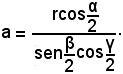
Formule analoghe si trovano per i lati b e c.
Altri casi interessanti di risoluzione si ottengono quando non si assegnano più elementi distinti di un triangolo, ma convenienti combinazioni. Anche su questo argomento ci si limita ad esporre alcuni tra i casi più caratteristici.
5° caso
-risoluzione di un triangolo, conoscendo un lato, l'angolo opposto e la somma o la differenza degli altri due lati.
Indicando con a il lato, con α l'angolo opposto e con s la somma degli altri due lati, cioè s = a + b, dalla formula seguente di Delambre:
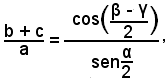
si ottiene
Mediante le tavole, si ricava il valore di
e quindi di β - γ.
Indicando tale valore con φ, si ottiene allora il sistema
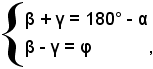
da cui, sommando e sottraendo, si deducono i valori
Ottenuti così i tre angoli, dal teorema dei seni si ricavano i valori dei lati a, b, c.
Se invece si conosce la differenza d = b - c, dalla formula di Delambre, cioè da
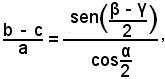
Se invece si conosce la differenza d = b - c, dalla formula di Delambre, cioè da
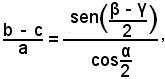
si ottiene
da cui si ricava il valore di
e quindi di β - γ.
Si procede poi come nel caso precedente.
Questo esempio di risoluzione dei triangoli si presta ad una semplice costruzione geometrica, supponendo di conoscere:
a)-il lato a, l'angolo α e la somma s = b + c degli altri due lati.
Si costruisce l'angolo
di vertice O e sul lato s si traccia un segmento
Successivamente si traccia la circonferenza di centro C e raggio a, che incontra l'altro lato r dell'angolo
nei due punti B1, B2, supponendo che tali intersezioni esistano.Indicati poi con M1, M2 i punti medi dei due segmenti OB1, OB2, si conducono da tali punti le perpendicolari ad r fino ad incontrare il lato s nei punti A1, A2, supponendo sempre che tali intersezioni esistano.
I due triangoli A1B1C, A2B2C soddisfano le condizioni date.
Infatti, si considera il triangolo A1B1C, nel quale il lato CB1 è per costruzione uguale ad a.
Poichè A1 è sull'asse del segmento OB1, risulta A1B1 = A1O e quindi:
Inoltre,
e perciò l'angolo
, come supplementare di , è uguale ad α, e ciò dimostra quanto asserito.Per l'altro triangolo A2B2C il ragionamento è analogo.
Si suppone ora di conoscere:
b)-la differenza d = b - c.
Si costruisce l'angolo
di vertice O e sul lato s si riporta un segmento
Successivamente si traccia la circonferenza di centro C e raggio a, che incontra l'altro lato r in un punto B.
Detto M il punto medio del segmento OB, da questo si conduce la perpendicolare ad r fino ad incontrare il prolungamento di s in A. Il triangolo ABC così ottenuto è quello richiesto.
Infatti, il lato CB è uguale ad a per costruzione, inoltre essendo l'angolo
l'angolo
in quanto suo supplementare.
Inoltre il triangolo OBA è isoscele, perchè A appartiene all'asse di OB e quindi l'angolo al vertice
èInfine risulta:
e ciò dimostra quanto asserito.
6° caso
-risoluzione di un triangolo, conoscendo un lato, un angolo ad esso adiacente e la somma o la differenza degli altri due.
Indicati con a il lato, con β l'angolo opposto e con s la somma degli altri due lati, cioè s = b + c, si parte dalla formule di Briggs relative alla tangente:
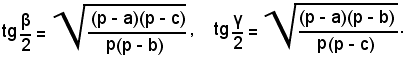
Moltiplicando membro a membro, si ottiene:
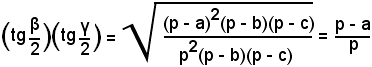
e quindi, sostituendo a p la sua espressione, risulta
Segue che:
da cui, mediante le tavole, si ottiene γ/2 e quindi γ; di conseguenza α = 180° - (β + γ). Ottenuti i tre angoli, mediante il teorema dei seni, si trovano i lati b e c.
Si suppone ora di conoscere la differenza d = b - c; si parte ancora dalle formule di Briggs relative alla tangente e, dividendole membro a membro, si ha:
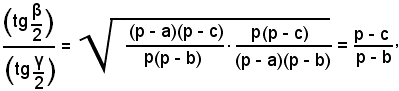
da cui
Mediante le tavole, da questa relazione si ottiene γ/2 e quindi γ; di conseguenza α = 180° - (β + γ). Ottenuti i tre angoli, mediante il teorema dei seni, si trovano i lati b e c.
Anche questi due modi di risoluzione si prestano ad una costruzione geometrica molto semplice:
a)-si costruisce un angolo
di vertice B.Si prende sul lato r il segmento
e su s il segmento .Si congiunge poi C con D e, detto M il punto medio di CD, si conduce da M la perpendicolare alla CD fino ad incontrare s in A.
Si vuole dimostrare che il triangolo ABC così ottenuto soddisfa le condizioni date.
Infatti, tale triangolo ha il lato
e l'angolo in , per costruzione; inoltre poichè A si trova sull'asse del segmento DC, risulta AC = DA, da cui,e ciò dimostra quanto asserito.
b)-Nel caso in cui si conosce la differenza b - c, si riporta sul prolungamento s' del lato s il segmento
e sul lato r il segmento .Congiunto E con C, si conduce l'asse del segmento EC, fino ad incontrare il lato s in A; il triangolo ABC soddisfa le condizioni date.
Infatti, tale triangolo ha il lato
, l'angolo , per costruzione, inoltre siccome A si trova sull'asse del segmento EC, risulta EA = AC, pertanto si ha:e ciò dimostra quanto asserito.
Nota bene
Queste costruzioni conservano naturalmente un loro preciso significato sotto l'ipotesi che effettivamente esistano i vari punti d'incontro di cui si parla. La ricerca delle condizioni, sotto le quali ciò avviene effettivamente, porterebbe alla determinazione di certe condizioni analitiche che rappresenterebbero il risultato della discussione. Tale ricerca si omette.
7° caso
-risoluzione di un triangolo, conoscendo i raggi dei cerchi ex-inscritti.
Indicando tali raggi con ra, rb, rc, dalle formule
moltiplicandole a due a due, si ha:
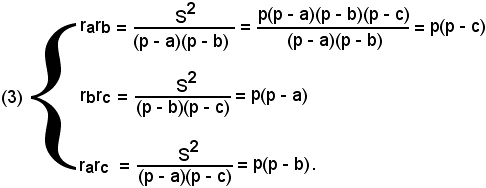
Sommando membro a membro, segue:
rarb + rbrc + rarc = p(p - c) + p(p - a) + p(p - b) = p[3p - (a + b + c)] = p(3p - 2p) = p2
e quindi
Inoltre, risolvendo la prima delle (3) rispetto a c, si ottiene:
rarb = p2 - pc,
da cui
e per la formula (4)
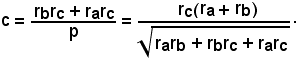
Per gli altri due lati a e b si procede analogamente.
Per ottenere gli angoli ci si serve delle formule di Briggs relative alle tangenti, si ha:
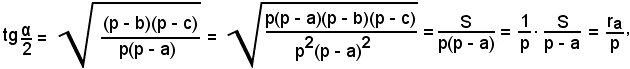
o anche
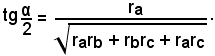
Si procede analogamente per:
Applicazioni della trigonometria negli altri campi
Moltissime applicazioni della trigonometria si trovano nella geodesia, nella topografia e nell'astronomia. Si accennano soltanto alcuni problemi semplici ed elementari, osservando che in questi campi le misure delle lunghezze e degli angoli, relative ai dati del problema in esame, vengono eseguite con metodi molto accurati, mediante strumenti di precisione, come livelli azimutali, teodoliti, tacheometri, stadie e cannocchiali anallattici.
Problema 1 - Calcolare l'altezza di una torre la cui cima sia inaccessibile.
Sia h l'altezza della torre, schematizzata in figura con il segmento BC; si misuri orizzontalmente sul terreno, a partire dal piede B della torre, una distanza a piacere
Si misuri poi l'angolo e, dal triangolo rettangolo ABC, si ha:h = atgα.
Se la distanza AB non è orizzontale, si indichi con H il punto in cui l'orizzontale per A incontra la vericale BC, come risulta dalle figure seguenti.
Si misurano allora da A gli angoli
Applicando il teorema dei seni al triangolo ABC, segue che:
siccome
è complementare di α, risulta Quindi:dove si considera il segno + o -, a seconda che B si trovi al di sotto o al di sopra dell'orizzontale AH.
Problema 2 - Calcolare la distanza di un punto da un altro visibile ma non accessibile.
Questo problema ha molta importanza in astronomia e in topografia, per il rilievo dei terreni.
Si suppone che i due punti A e C, visibili l'uno dall'altro, siano separati da un ostacolo, per esempio da un fiume. Fissato un punto B, si misura la distanza qualsiasi
, e poi gli angoliDetta x la distanza incognita AC, applicando il teorema dei seni al triangolo ABC, del quale si conoscono un lato e i due angoli adiacenti, risulta:
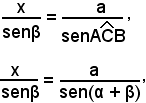
e quindi
Problema 3 (Problema di Hansen o di Snellius) - Calcolare la distanza fra due punti visibili, ma non accessibili.
Siano A, B i punti visibili da C, ma non accessibili; si misura una base qualsiasi
e poi i cinque angoliSe in particolare i punti A, B, C, D sono complanari, basta misurare solo gli angoli α, β, γ, δ, φ, perchè allora φ = α - β.
In ciascuno dei triangoli ACD, BCD si vengono così a conoscere un lato e due angoli, quindi si ha:
e si possono determinare i lati AC, BC.
Dal triangolo ABC infine, essendo noti i due lati AC, BC e l'angolo compreso φ, si trova la misura x del lato AB, ossia la distanza cercata.
Problema 4 (Problema di Pothenot o dei quattro punti).
Questo è il classico problema, molto importante in topografia.
Dati tre punti A, B, C, complanari, non allineati, e un quarto punto P, complanare con essi e posto internamente all'angolo convesso ABC, si tratta di calcolare le distanze di P dagli altri punti A, B, C.
Sono noti gli angoli
e i lati
S'introducono ora due angoli ausiliari x, y, ponendo:
Applicando il teorema dei seni a ciascuno dei triangoli ABP, BCP e ricordando che angoli supplementari hanno seni uguali, segue che:
da cui
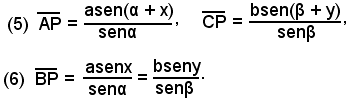
Da queste formule risulta evidente che, per trovare le distanze AP, BP, CP, occorre determinare gli angoli ausiliari x, y. Poichè la somma degli angoli interni di un quadrilatero è uguale a 360°, si ha:
x + y + α + β + φ = 360°,
quindi
x + y = 360° - (α + β + φ)
e si indica con ω.
Si calcola ora il valore della differenza x - y.
Dall'uguaglianza (6), si ha:
Allora si calcola l'angolo γ del I quadrante, tale che
Quindi si ha:
e perciò, per proprietà note delle proporzioni,
o anche, ricordando che tg45° = 1,
Per il teorema di Nepero, è noto che:
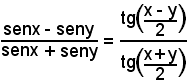
e si ha:
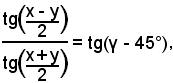
ossia
con ω noto.
Da questa relazione si ricava
e poi x - y; ponendo x - y = ρ, si deduce il sistema
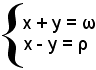
e si determinano facilmente gli angoli ausiliari x, y. Dopo di ciò, le distanze cercate sono date dalle formule (5) e (6).