MIKY & GENNY
ESEMPI DI IDENTITA', EQUAZIONI E SISTEMI GONIOMETRICI ---> INDICE
Con
l'impiego delle formule finora trattate si possono verificare altre
identità, risolvere equazioni goniometriche particolari e
sistemi.
Esempi di identità
1)-Verificare l'identità:
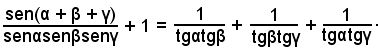
Trasformando sen(α + β + γ) mediante la formula di addizione, si ha:
sen(α + β + γ) = senαcosβcosγ + cosαsenβcosγ + cosαcosβsenγ - senαsenβsenγ.
Dividendo ambo i membri per senαsenβsenγ, risulta:
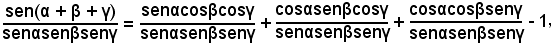
cioè
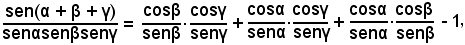
o anche
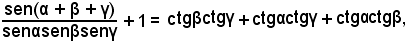
da cui segue
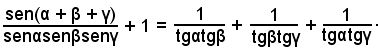
Quindi, risulta verificata l'identità.
2)-Siano α, β, γ, i tre angoli di un triangolo, verificare l'identità subordinata:
(1) tgα + tgβ + tgγ = tgαtgβtgγ.
Dalle ipotesi risulta:
α + β = 180° - γ,
allora
tg(α + β) = -tgγ.
Trasformando tg(α + β) mediante la formula di addizione, segue
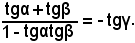
Inoltre, trasportando e riducendo a forma intera, risulta:
tgα + tgβ + tgγ(1 - tgαtgβ) = 0,
e quindi sviluppando
tgα + tgβ + tgγ - tgαtgβtgγ = 0,
ossia
tgα + tgβ + tgγ = tgαtgβtgγ.
Quindi, risulta verificata l'identità.
Si effettua ora una verifica numerica: sia α = β = γ = 60°; essendo tg60° =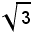
, dalla (1) segue:
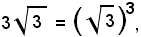
perchè
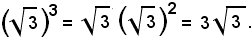
Se α = β = 30°, γ = 120°, poichè
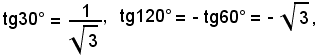
dalla (1) si deduce
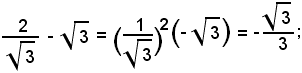infatti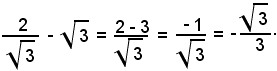
3)-Siano α, β, γ, i tre angoli di un triangolo, verificare l'identità subordinata:
Dalle ipotesi risulta:
α = 180° - (β + γ),
allora
sen2α = senαsenα = senαsen(β + γ) = senα(senβcosγ + cosβsenγ),
sen2β = senβsenβ = senβsen(α + γ) = senβ(senαcosγ + cosαsenγ),
sen2γ = senγsenγ = senγsen(α + β) = senγ(senαcosβ + cosαsenβ),
da cui, sviluppando e sommando membro a membro, si ha
sen2α + sen2β + sen2γ = 2(senαsenβcosγ + senαcosβsenγ + cosαsenβsenγ),
da cui, dividendo per 2,
Quindi, risulta verificata l'identità.
4)-Verificare l'identità:
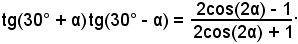
Trasformando il primo membro mediante le formule di addizione e sottrazione, si ha:
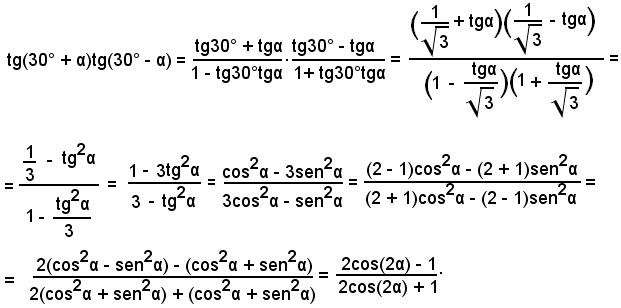
5)-Verificare l'identità:
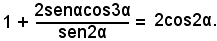
Sviluppando e applicando le formule di prostaferesi, ha:
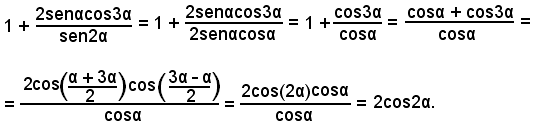
6)-Verificare l'identità:
cosα + cos(α + 120°) - cos(α + 60°) = 0.
Applicando la formula di prostaferesi del coseno ai primi due addendi del primo membro, si ha:
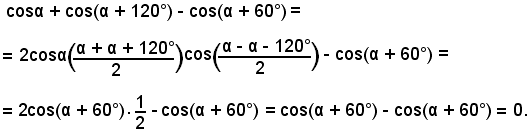
7)-Verificare l'identità:
sen(α + β)cos(α - β) + sen(β + γ)cos(β - γ) + sen(γ + α)cos(γ - α) = sen(2α) + sen(2β) + sen(2γ)e se nella formula
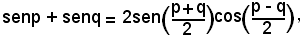
si pone
p = a + b, q = a - b,
e quindi
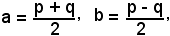
risulta
sen(a + b) + sen(a - b) = 2senacosb,
e quindi anche
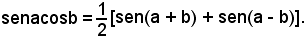
da cui, sommando membro a membro, si deduce che il primo membro dell'identità diventa
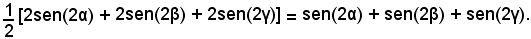
Esempi di equazioni
Si trattano ora degli esempi di equazioni in cui figurano, in generale, angoli e funzioni diverse.
In tal caso, la prima operazione che si deve effettuare è quella di trasformare, se è possibile, le funzioni contenenti angoli diversi in altre con lo stesso angolo e poi seguire il procedimento già trattato.
1)-Risolvere l'equazione:
tg(45° - x) + tg(45° + x) + 4 = 0.
Applicando le formule di addizione e sottrazione, si ha:
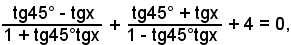
o anche, essendo tg45° = 1,
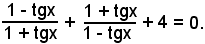
Riducendo a forma intera, si ha:
(1 - tgx)2 + (1 + tgx)2+ 4(1 - tgx2) = 0,
e quindi sviluppando e semplificando,
2tgx2 - 6 = 0,
da cui
tgx2 = 3,
cioè
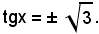
Se
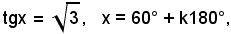
o anche
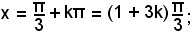
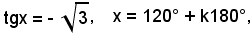
o anche
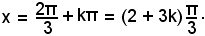
2)-Risolvere l'equazione:
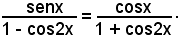
Applicando la formula di duplicazione del coseno, si ha:
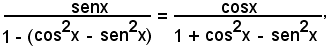
o anche, liberando dalle parentesi,
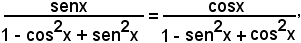
e quindi
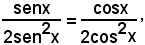
cioè
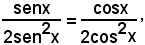
segue
senx = cosx,
cioè
tgx =1,
e perciò
x = 45° + k180°,
o anche
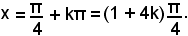
3)-Risolvere l'equazione:
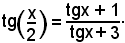
Se nella formula di duplicazione della tangente, cioè
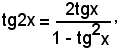
si scrive x/2 al posto di x ed x al posto di 2x, risulta:
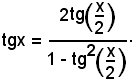
Sostituendo tale espressione nel secondo membro dell'equazione data, si ottiene:
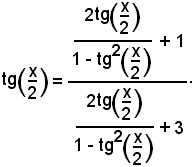
Semplificando il secondo membro, risulta:
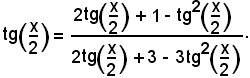
Posto tg(x/2) = t, si ha l'equazione algebrica:
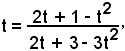
o anche, riducendo a forma intera
t(2t + 3 - 3t2) = 2tg + 1 - t2,
cioè
(t - 1)(3t2 - 1) = 0.
Si hanno quindi le due equazioni
t - 1 = 0, 3t2 - 1 = 0.
Ricordando che t = tg(x/2), segue:
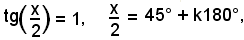
cioè
x = 90° + 2k180°,
o anche
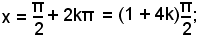
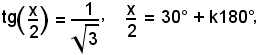
cioè
x = 60° + 2k180°,
o anche
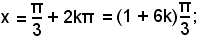
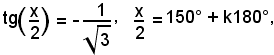
cioè
x = 300° + 2k180°,
o anche
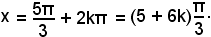
4)-Risolvere l'equazione:
sen(5x) = -sen(3x) = 0.
Applicando al primo membro le formule di prostaferesi, si ha:
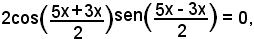
cioè, semplificando
senx = 0, cos(4x) = 0.
Segue:
senx = 0, x = k180°,
o anche
x = kπ;
cos(4x) = 0, 4x = 90° + k180°,
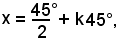
o anche
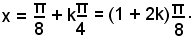
5)-Risolvere l'equazione:
cos(6x) - cos(2x) + sen(4x) = 0.
Applicando le formule di prostaferesi, si ha:
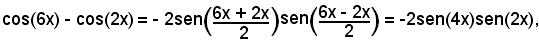
e quindi l'equazione data si trasforma in
-2sen(4x)sen(2x) + sen(4x) = 0,
o anche
sen(4x)[1 - 2sen(2x)] = 0,
da cui
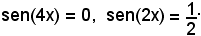
Segue
sen(4x) = 0, 4x = k180°, x = 45°,
o anche
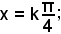
6)-Risolvere l'equazione:
tg(3x) + tg(2x) = tg(4x) + tgx.
Trasportando opportunamente i termini, si può scrivere
tg(3x) - tgx = tg(4x) - tg(2x)
e, applicando le formule di prostaferesi, si ha:
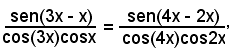
cioè
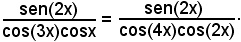
Semplificando, si ha:
(*) cos(3x)cosx, cos(4x)cos(2x).
Se ora nella formula di prostaferesi
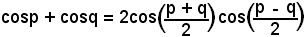
si pone
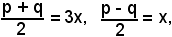
e quindi
p = 4x, q = 2x
si ha
2cos(3x)cosx = cos(4x) + cos(2x);
analogamente, se si pone
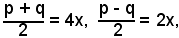
e quindi
p = 6x, q = 2x,
risulta
2cos(4x)cos(2x) = cos(6x) + cos(2x).
Sostituendo questi risultati nella (*), si deduce:
cos(4x) = cos(6x),
o anche
cos(6x) - cos(4x) = 0.
Applicando a quest'ultima le formule di prostaferesi, segue:
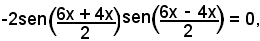
cioè
sen(5x)senx = 0
e quindi
sen(5x) = 0; 5x = k180°, x = 36°,
o anche
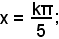
o anche
x = kπ.
7)-Risolvere l'equazione:
1 + senx + cosx + tgx = 0.
Per le formule di prostaferesi, si ha:
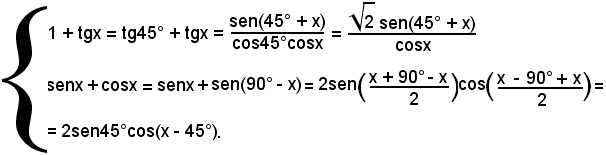
Allora, se si sostiruiscono queste espressioni nell'equazione data, si ottiene
o anche
sen(45° + x) + cosxcos(45° - x) = 0.
Poichè 45° - x è complementare di 45° + x, si deduce
cos(45° - x) = sen(45° + x)
e quindi l'equazione si trasforma in
sen(45° + x) + sen(45° + x)cosx = 0,
o anche
sen(45° + x)(1 + cosx) = 0,
da cui
sen(45° + x) = 0, cosx + 1 = 0,
e quindi
sen(45° + x) = 0; 45° + x = k180°, x = -45° + k180°,
oppure
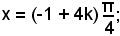
cosx = -1; x = 180° + k360°,
oppure
x = π + 2kπ = (1 + 2k)π.
Si osserva che si poteva procedere direttamente, anche se meno rapidamente, applicando all'equazione sen(45° + x) + cosxcos(45° - x) = 0 le formule di addizione e sottrazione.
Esempi di sistemi
1)-Risolvere il sistema:
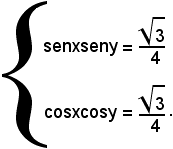
Sommando e sottraendo membro a membro, si ottiene il sistema equivalente:
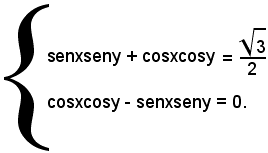
Applicando le formule di addizione e sottrazione, si ha:
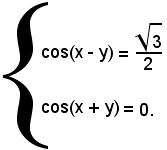
Quindi:
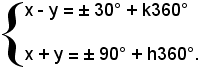
Risolvendo questo sistema di due equazioni in due incognite col metodo di addizione e sottrazione, si ha:
oppure
2)-Risolvere il sistema
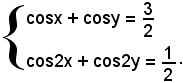
Dalla prima equazione si deduce
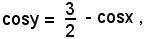
ed elevando al quadrato,
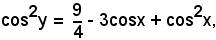
e quindi
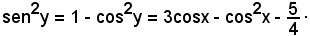
Allora si ha:
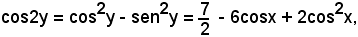
e sostituendo questa espressione nella seconda equazione del sistema, segue
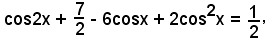
o anche
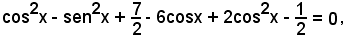
cioè
3cos2x - sen2x - 6cosx + 3 = 0.
Eliminando sen2x = 1 - cos2x e semplificando, si ha l'equazione di secondo grado in cosx:
2cos2x - 3cosx + 1 = 0.
Risolvendo, si trovano per cosx i valori 1 e 1/2, ai quali corrispondono per cosy i valori 1/2 e 1;
quindi segue:
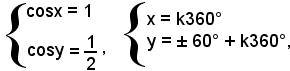
o anche
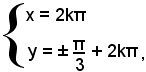
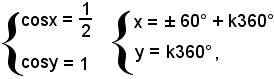
o anche
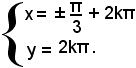
Esempi di identità
1)-Verificare l'identità:
Trasformando sen(α + β + γ) mediante la formula di addizione, si ha:
Dividendo ambo i membri per senαsenβsenγ, risulta:
cioè
o anche
da cui segue
Quindi, risulta verificata l'identità.
2)-Siano α, β, γ, i tre angoli di un triangolo, verificare l'identità subordinata:
(1) tgα + tgβ + tgγ = tgαtgβtgγ.
Dalle ipotesi risulta:
α + β = 180° - γ,
allora
tg(α + β) = -tgγ.
Trasformando tg(α + β) mediante la formula di addizione, segue
Inoltre, trasportando e riducendo a forma intera, risulta:
tgα + tgβ + tgγ(1 - tgαtgβ) = 0,
e quindi sviluppando
tgα + tgβ + tgγ - tgαtgβtgγ = 0,
ossia
tgα + tgβ + tgγ = tgαtgβtgγ.
Quindi, risulta verificata l'identità.
Si effettua ora una verifica numerica: sia α = β = γ = 60°; essendo tg60° =
, dalla (1) segue:perchè
Se α = β = 30°, γ = 120°, poichè
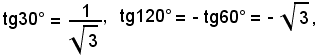
dalla (1) si deduce
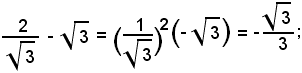
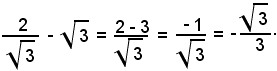
3)-Siano α, β, γ, i tre angoli di un triangolo, verificare l'identità subordinata:
Dalle ipotesi risulta:
α = 180° - (β + γ),
allora
sen2α = senαsenα = senαsen(β + γ) = senα(senβcosγ + cosβsenγ),
da cui, sviluppando e sommando membro a membro, si ha
sen2α + sen2β + sen2γ = 2(senαsenβcosγ + senαcosβsenγ + cosαsenβsenγ),
da cui, dividendo per 2,
Quindi, risulta verificata l'identità.
4)-Verificare l'identità:
Trasformando il primo membro mediante le formule di addizione e sottrazione, si ha:
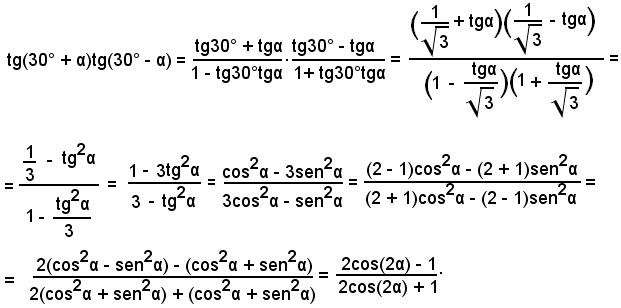
5)-Verificare l'identità:
Sviluppando e applicando le formule di prostaferesi, ha:
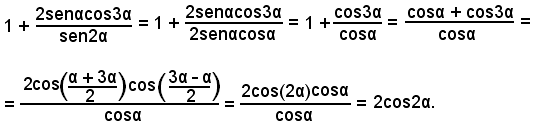
6)-Verificare l'identità:
cosα + cos(α + 120°) - cos(α + 60°) = 0.
Applicando la formula di prostaferesi del coseno ai primi due addendi del primo membro, si ha:
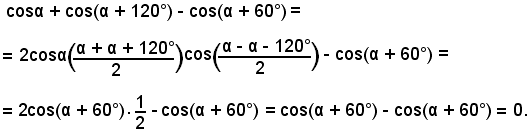
7)-Verificare l'identità:
sen(α + β)cos(α - β) + sen(β + γ)cos(β - γ) + sen(γ + α)cos(γ - α) = sen(2α) + sen(2β) + sen(2γ)e se nella formula
si pone
p = a + b, q = a - b,
e quindi
risulta
sen(a + b) + sen(a - b) = 2senacosb,
e quindi anche
Applicando tale formula ai singoli addendi del primo membro dell'identità, si ha:
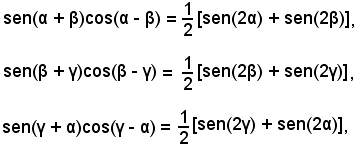
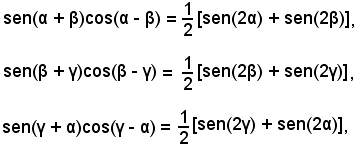
da cui, sommando membro a membro, si deduce che il primo membro dell'identità diventa
Esempi di equazioni
Si trattano ora degli esempi di equazioni in cui figurano, in generale, angoli e funzioni diverse.
In tal caso, la prima operazione che si deve effettuare è quella di trasformare, se è possibile, le funzioni contenenti angoli diversi in altre con lo stesso angolo e poi seguire il procedimento già trattato.
1)-Risolvere l'equazione:
Applicando le formule di addizione e sottrazione, si ha:
o anche, essendo tg45° = 1,
Riducendo a forma intera, si ha:
(1 - tgx)2 + (1 + tgx)2+ 4(1 - tgx2) = 0,
e quindi sviluppando e semplificando,
da cui
tgx2 = 3,
cioè
Se
o anche
se
o anche
2)-Risolvere l'equazione:
Applicando la formula di duplicazione del coseno, si ha:
o anche, liberando dalle parentesi,
e quindi
cioè
segue
senx = cosx,
cioè
tgx =1,
e perciò
x = 45° + k180°,
o anche
3)-Risolvere l'equazione:
Se nella formula di duplicazione della tangente, cioè
si scrive x/2 al posto di x ed x al posto di 2x, risulta:
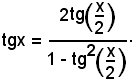
Sostituendo tale espressione nel secondo membro dell'equazione data, si ottiene:
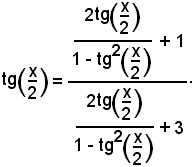
Semplificando il secondo membro, risulta:
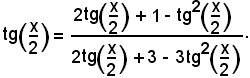
Posto tg(x/2) = t, si ha l'equazione algebrica:
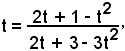
o anche, riducendo a forma intera
t(2t + 3 - 3t2) = 2tg + 1 - t2,
cioè
(t - 1)(3t2 - 1) = 0.
Si hanno quindi le due equazioni
t - 1 = 0, 3t2 - 1 = 0.
Ricordando che t = tg(x/2), segue:
cioè
x = 90° + 2k180°,
o anche
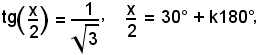
cioè
x = 60° + 2k180°,
o anche
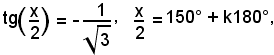
cioè
x = 300° + 2k180°,
o anche
4)-Risolvere l'equazione:
Applicando al primo membro le formule di prostaferesi, si ha:
cioè, semplificando
cos(4x)senx = 0,
e quindi
senx = 0, cos(4x) = 0.
Segue:
senx = 0, x = k180°,
o anche
o anche
5)-Risolvere l'equazione:
Applicando le formule di prostaferesi, si ha:
e quindi l'equazione data si trasforma in
-2sen(4x)sen(2x) + sen(4x) = 0,
o anche
sen(4x)[1 - 2sen(2x)] = 0,
da cui
Segue
sen(4x) = 0, 4x = k180°, x = 45°,
o anche
6)-Risolvere l'equazione:
tg(3x) + tg(2x) = tg(4x) + tgx.
Trasportando opportunamente i termini, si può scrivere
tg(3x) - tgx = tg(4x) - tg(2x)
e, applicando le formule di prostaferesi, si ha:
cioè
Semplificando, si ha:
(*) cos(3x)cosx, cos(4x)cos(2x).
Se ora nella formula di prostaferesi
si pone
e quindi
p = 4x, q = 2x
si ha
2cos(3x)cosx = cos(4x) + cos(2x);
analogamente, se si pone
e quindi
p = 6x, q = 2x,
risulta
2cos(4x)cos(2x) = cos(6x) + cos(2x).
Sostituendo questi risultati nella (*), si deduce:
cos(4x) = cos(6x),
o anche
cos(6x) - cos(4x) = 0.
Applicando a quest'ultima le formule di prostaferesi, segue:
cioè
sen(5x)senx = 0
e quindi
sen(5x) = 0; 5x = k180°, x = 36°,
o anche
senx = 0; x = k180°,
o anche
x = kπ.
7)-Risolvere l'equazione:
1 + senx + cosx + tgx = 0.
Per le formule di prostaferesi, si ha:
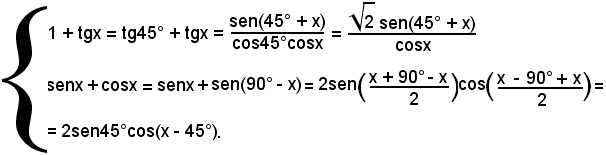
Allora, se si sostiruiscono queste espressioni nell'equazione data, si ottiene
o anche
sen(45° + x) + cosxcos(45° - x) = 0.
Poichè 45° - x è complementare di 45° + x, si deduce
cos(45° - x) = sen(45° + x)
e quindi l'equazione si trasforma in
sen(45° + x) + sen(45° + x)cosx = 0,
o anche
sen(45° + x)(1 + cosx) = 0,
da cui
sen(45° + x) = 0, cosx + 1 = 0,
e quindi
sen(45° + x) = 0; 45° + x = k180°, x = -45° + k180°,
oppure
cosx = -1; x = 180° + k360°,
oppure
x = π + 2kπ = (1 + 2k)π.
Si osserva che si poteva procedere direttamente, anche se meno rapidamente, applicando all'equazione sen(45° + x) + cosxcos(45° - x) = 0 le formule di addizione e sottrazione.
Esempi di sistemi
1)-Risolvere il sistema:
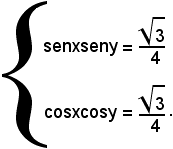
Sommando e sottraendo membro a membro, si ottiene il sistema equivalente:
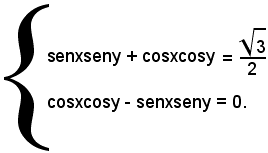
Applicando le formule di addizione e sottrazione, si ha:
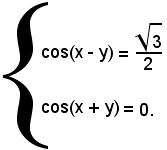
Quindi:
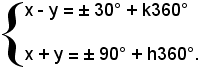
Risolvendo questo sistema di due equazioni in due incognite col metodo di addizione e sottrazione, si ha:
oppure
2)-Risolvere il sistema
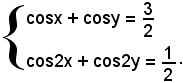
Dalla prima equazione si deduce
ed elevando al quadrato,
e quindi
Allora si ha:
e sostituendo questa espressione nella seconda equazione del sistema, segue
o anche
cioè
3cos2x - sen2x - 6cosx + 3 = 0.
Eliminando sen2x = 1 - cos2x e semplificando, si ha l'equazione di secondo grado in cosx:
2cos2x - 3cosx + 1 = 0.
Risolvendo, si trovano per cosx i valori 1 e 1/2, ai quali corrispondono per cosy i valori 1/2 e 1;
quindi segue:
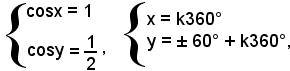
o anche
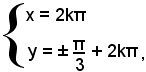
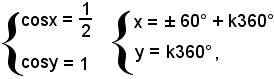
o anche