MIKY & GENNY
FORMULE DI BISEZIONE ---> INDICE
Le formule di bisezione si ricavano dal sistema formato dalla formula di duplicazione del coseno e dalla relazione fondamentale:

sommando e sottraendo membro a membro, si ricava
2cos2α = 1 + cos2α, 2sen2α = 1 - cos2α,
da cui, dividendo ambo i membri per 2, si ha:
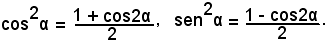
Sostituendo α/2 ad α, α a 2α ed estraendo la radice quadrata da ambo i membri, si ha:
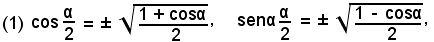
e dividendo membro a membro, si ottiene
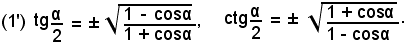
Le (1) e le (1'), che esprimono le funzioni goniometriche dell'angolo α/2 in funzione del coseno dell'angolo α, si chiamano formule di bisezione.
Si osserva che i doppi segni che compaiono al secondi membri di (1) e (1') non si possono eliminare, a meno che non si conosca, oltre al coseno, anche l'angolo, e quindi il quadrante a cui esso appartiene. Inoltre, i doppi segni di (1) e (1') sono indipendenti gli uni dagli altri.
Esempi
1)-Appicando le formule di bisezione, trovare i valori delle funzioni goniometriche dell'angolo di 15°.
Osservato che 15° = 30°/2, dalle (1) si ottiene:
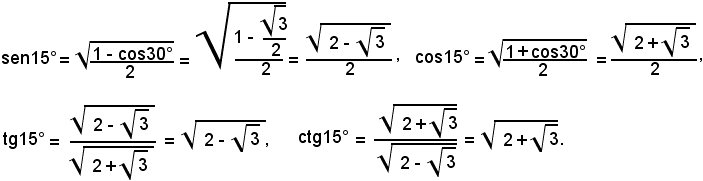
Si ricorda ora che nell'esempio relativo alle formule di addizione e sottrazione si è trovato:
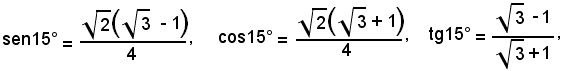
quindi questi valori devono coincidere con quelli precedenti. La verifica è immediata, se si ricordano le formule di trasformazione dei radicali doppi. Infatti, si ha:
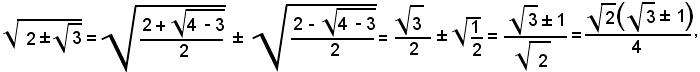
da cui,
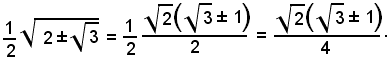
Le formule (1) e (1') esprimono le funzioni goniometriche dell'angolo α/2 con il solo coseno; con procedimento analogo si possono esprimere le funzioni goniometriche con il solo seno; si ottengono però formule più complicate e di scarso impiego.
Partendo dalla formula di duplicazione del seno, si considera il seguente sistema:
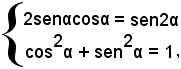
da cui, sommando e sottraendo membro a membro, si ha


sommando e sottraendo membro a membro, si ricava
2cos2α = 1 + cos2α, 2sen2α = 1 - cos2α,
da cui, dividendo ambo i membri per 2, si ha:
Sostituendo α/2 ad α, α a 2α ed estraendo la radice quadrata da ambo i membri, si ha:
e dividendo membro a membro, si ottiene
Le (1) e le (1'), che esprimono le funzioni goniometriche dell'angolo α/2 in funzione del coseno dell'angolo α, si chiamano formule di bisezione.
Si osserva che i doppi segni che compaiono al secondi membri di (1) e (1') non si possono eliminare, a meno che non si conosca, oltre al coseno, anche l'angolo, e quindi il quadrante a cui esso appartiene. Inoltre, i doppi segni di (1) e (1') sono indipendenti gli uni dagli altri.
Esempi
1)-Appicando le formule di bisezione, trovare i valori delle funzioni goniometriche dell'angolo di 15°.
Osservato che 15° = 30°/2, dalle (1) si ottiene:
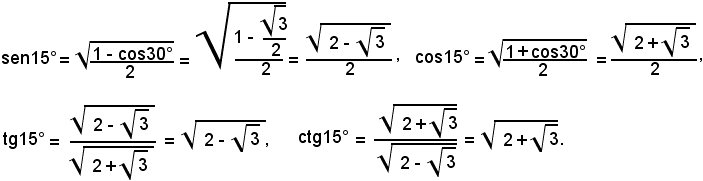
Si ricorda ora che nell'esempio relativo alle formule di addizione e sottrazione si è trovato:
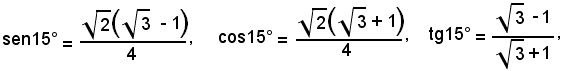
quindi questi valori devono coincidere con quelli precedenti. La verifica è immediata, se si ricordano le formule di trasformazione dei radicali doppi. Infatti, si ha:
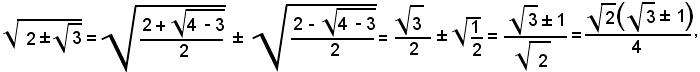
da cui,
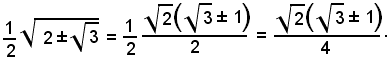
Le formule (1) e (1') esprimono le funzioni goniometriche dell'angolo α/2 con il solo coseno; con procedimento analogo si possono esprimere le funzioni goniometriche con il solo seno; si ottengono però formule più complicate e di scarso impiego.
Partendo dalla formula di duplicazione del seno, si considera il seguente sistema:
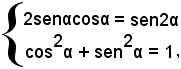
da cui, sommando e sottraendo membro a membro, si ha

o anche
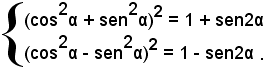
Estraendo la radice quadrata da ambo i membri, risulta
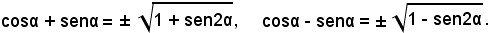
Per semplicità di scrittura si omettono i doppi segni davanti ai radicali, inoltre si deve tenere conto che essi sono indipendenti l'uno dall'altro.
Sommando e sottraendo membro a membro, si ha:
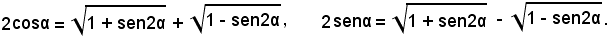
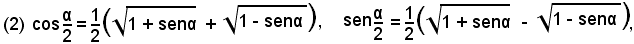
e quindi anche

Alcune volte è utile conoscere altre formule di bisezione relative alla tangente e alla cotangente; esse si trovano immediatamente razionalizzando la (1'). Si parte quindi dalla formula
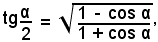
e si rende razionale il denominatore, con i procedimenti algebrici:
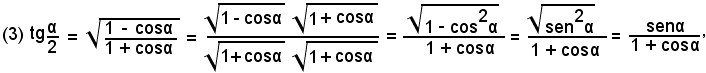
ed anche
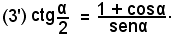
Analogamente, se si rende razionale il numeratore, si trova:

ed anche
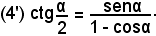
Esempio - Calcolare le funzioni goniometriche della somma dei tre angoli α, β e γ.
Considerando α + β + γ = (α + β) + γ e applicando le formule di addizione, si ha:
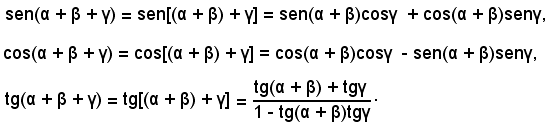
Sostituendo in queste formule alle funzioni
sen(α + β), cos(α + β), tg(α + β)
le espressioni date dalle formule di addizione, si ha:

Analogamente si possono ottenere le funzioni goniometriche della somma di un numero qualsiasi di angoli.
In particolare, se si suppone α = β = γ, dalle formule precedenti si ricava:
sen(3α) = 3senαcos2α - senα3α = 3senα(1 - senα2α) - senα3α = 3senα - 4senα3α,
cos(3α) = cosα3α - 3senα2αcosα = cosα3α - 3(1 - cosα2)cosα = 4cosα3α - 3cosα,
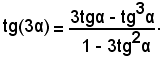
Tali formule si chiamano formule di triplicazione.
Nota bene
La formula della tangente si può ottenere anche in altro modo, cioè dividendo membro a membro le espressioni di sen(3α) e cos(3α), ottenendo:

Esprimendo senα2α e cosα2 in funzione di tgα, si ha:
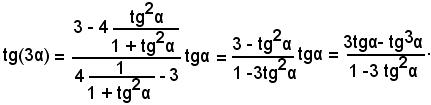
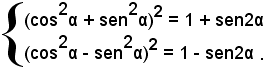
Estraendo la radice quadrata da ambo i membri, risulta
Per semplicità di scrittura si omettono i doppi segni davanti ai radicali, inoltre si deve tenere conto che essi sono indipendenti l'uno dall'altro.
Sommando e sottraendo membro a membro, si ha:
Sostituendo α/2 ad α, ed α a 2α, inoltre, estraendo la radice quadrata da ambo i membri, si ha:
e quindi anche

Alcune volte è utile conoscere altre formule di bisezione relative alla tangente e alla cotangente; esse si trovano immediatamente razionalizzando la (1'). Si parte quindi dalla formula
e si rende razionale il denominatore, con i procedimenti algebrici:
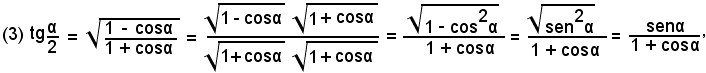
ed anche
Analogamente, se si rende razionale il numeratore, si trova:

ed anche
Esempio - Calcolare le funzioni goniometriche della somma dei tre angoli α, β e γ.
Considerando α + β + γ = (α + β) + γ e applicando le formule di addizione, si ha:
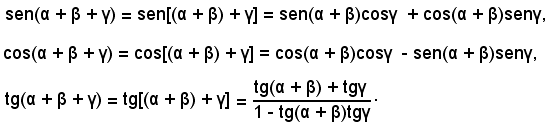
Sostituendo in queste formule alle funzioni
sen(α + β), cos(α + β), tg(α + β)
le espressioni date dalle formule di addizione, si ha:

Analogamente si possono ottenere le funzioni goniometriche della somma di un numero qualsiasi di angoli.
In particolare, se si suppone α = β = γ, dalle formule precedenti si ricava:
sen(3α) = 3senαcos2α - senα3α = 3senα(1 - senα2α) - senα3α = 3senα - 4senα3α,
cos(3α) = cosα3α - 3senα2αcosα = cosα3α - 3(1 - cosα2)cosα = 4cosα3α - 3cosα,
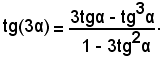
Tali formule si chiamano formule di triplicazione.
Nota bene
La formula della tangente si può ottenere anche in altro modo, cioè dividendo membro a membro le espressioni di sen(3α) e cos(3α), ottenendo:

Esprimendo senα2α e cosα2 in funzione di tgα, si ha: