MIKY & GENNY
FUNZIONI GONIOMETRICHE ---> INDICE
Si
consideri una circonferenza di centro O e raggio r e due suoi diametri
fra loro perpendicolari AA', BB', orientati in modo tale da poterli
assumere come assi cartesiani, e sia AP un qualsiasi arco orientato, al
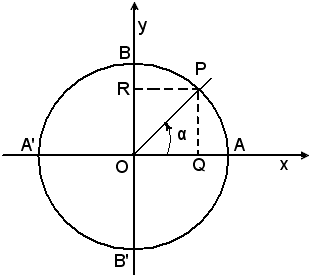
quale corrisponda l'angolo 
Si traccino da P le perpendicolari PQ e PR agli assi cartesiani, e si
considerino le misure dei segmenti orientati QP = OR e OQ, rispetto al
raggio OA della circonferenza, scelto come unità di misura,
cioè si considerino i rapporti fra i segmenti orientati
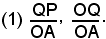
Si dimostra facilmente che questi rapporti non dipendono dalla particolare circonferenza di riferimento, ma solo dall'angolo al centro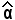
corrispondente all'arco 
; in altri termini sussiste il seguente teorema:
-i due rapporti (1) dipendono solo dalla misura dell'arco.
Per dimostrare il teorema è sufficiente provare che, presi su due circonferenze diverse due arch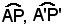i
corrispondenti allo stesso angolo al centro, e quindi aventi la stessa
misura in radianti, i precedenti rapporti risultano uguali.
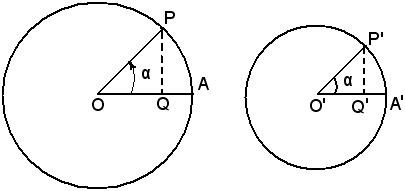
A tale scopo, si considerano due circonferenze di centri O, O' e di raggi OA, O'A' e siano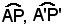 due archi corrispondenti allo stesso angolo al centro 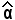; tracciando da P e da P' le perpendicolari PQ e P'Q' ai raggi OA, O'A', si ottengono i
due triangoli rettangoli OQP, O'Q'P', che risultano simili tra loro per
avere gli angoli uguali ed allora i lati corrispondenti sono in
proporzione.
Quindi, si può scrivere:
QP : OP = Q'P' : O'P'; OQ : OP = O'Q' = O'P',
o anche, essendo OP = OA e O'P' = O'A',
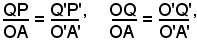
come dovevasi dimostrare.
Questo teorema permette di affermare che i rapporti
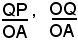
risultano esclusivamente funzioni dell'angolo α; resta quindi giustificata la seguente definizione:
-i due rapporti
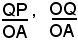
si chiamano funzioni goniometriche dell'angolo α, oppure funzioni circolari dell'arco.
Queste funzioni si indicano con le scritture
senα, cosα,
e si leggono rispettivamente seno di α e coseno di α, sioè si pone per definizione:
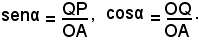
Si osserva ora che le misure dei due segmenti orientati OQ e QP rappresentano rispettivamente l'ascissa e l'ordinata del generico punto P della circonferenza; allora, prendendo come unità di misura il suo raggio, si può enunciare la seguente proprietà:
-il coseno e il seno di un arco rappresentano rispettivamente
l'ascissa e l'ordinata dell'estremo P dell'arco, in un sistema
cartesiano avente per assi i diametri tra loro ortogonali AA', BB' e
nel quale si assuma il raggio come unità di misura.
Quando si assume come unità di misura delle lunghezze il raggio di una data circonferenza e si prendono come assi cartesiani due diametri fra loro ortogonali, la circonferenza stessa si chiama circonferenza o cerchio trigonometrico.
Pertanto, la precedente proprietà si può enunciare in modo più semplice.
-il coseno e il seno di un arco del cerchio trigonometrico rappresentano rispettivamente l'ascissa e l'ordinata dell'estremo P dell'arco nel sistema cartesiano avente per asse delle x la retta individuata dal diametro OA, orientata da O verso A.
Altra definizione di seno e coseno
Le due funzioni seno e coseno, appena definite mediante il cerchio trigonometrico, si possono definire anche direttamente, partendo da un angolo qualsiasi.
Infatti, considerato un angolo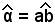
,
si fissi un sistema di assi cartesiani ortogonali avente per origine il
vertice O dell'angolo e come semiasse positivo delle x il lato a.
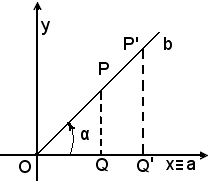
Si sceglie poi sull'altro lato b dell'angolo un punto P qualsiasi da cui si abbassa la perpendicolare PQ sul lato a e si considerano i due rapporti di segmenti orientati
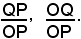
Si vede facilmente che questi rapporti non dipendono dal particolare punto P scelto sul lato b, ma solo dall'angolo considerato.
Infatti, preso un qualsiasi altro punto P' su b, da questo si abbassa la perpendicolare P'Q' su a; i due triangoli rettangoli OQP OQ'P', così ottenuti, sono simili fra loro, perchè hanno l'angolo
in comune, pertanto i lati omologhi sono in proporzione, quindi si puo scrivere
QP : OP = Q'P' : OP'; OQ : OP = OQ' : OP'
o anche
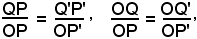
come dovevasi dimostrare.
I due rapporti
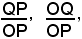
che dipendono solamente dalla misura dell'angolo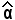, si dicono rispettivamente seno e coseno dell'angolo α.
Si dimostra ora che le funzioni così introdotte coincidono con le funzioni definite inizialmente.
Infatti, considerato l'angolo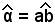, si costruisce la circonferenza di centro O e raggio OP, che incontra il lato a nel punto A.
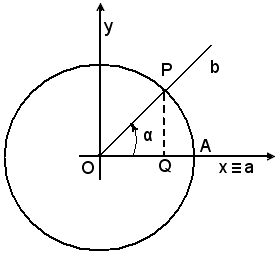
Si ottiene così l'arco orientato, le cui funzioni circolari seno e coseno sono proprio i rapporti
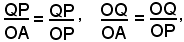
cioè sono le funzioni goniometriche dell'angolo α introdotte prima.
Per questa ragione le due funzioni seno e coseno si chiamano indifferentemente funzioni goniometriche, cioè misuratrici di un angolo, o funzioni circolari, o ciclometriche, cioè misuratrici di un arco.
Variazioni delle funzioni seno e coseno
Siccome il seno e il coseno di un angolo rappresentano le coordinate di un certo punto del cerchio trigonometrico, cerchio di raggio unitario, si può affermare che:
-in valore assoluto il seno e il coseno risultano sempre minori o uguali all'unità.
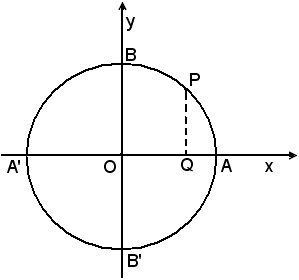
Inoltre, siccome le coordinate dei punti A e B del cerchio trigonometrico, sono A(1, 0), B(0, 1) e, quando il punto generico P coincide con A o con B, l'arco corrispondente ha misura 0° oppure 90°, si puo scrivere:
sen0° = 0, sen90° = 1, cos0° = 1, cos90° = 0.
Ragionando analogamente per i punti A' e B', le cui coordinate sono rispettivamente A'(-1, 0), B'(0, -1) ed osservando che quando il punto P coincide con A' o con B' l'arco corrispondente ha per misura 180° oppure 270°, si puo scrivere:
sen180° = 0, cos180° = -1, sen270° = -1, cos270° = 0.
Dopo questi primi risultati, si considera un arco di
estremo P variabile in modo che il punto P, partendo dalla posizione
iniziale A, vi ritorni dopo aver compiuto un intero giro e,
corrispondentemente si considera il relativo angolo al centro α,
che varierà a sua volta da 0° a 360°.
Quando l'angolo cresce da 0° a 90°, il segmento QP cresce continuamente fino a coincidere con il raggio OB.
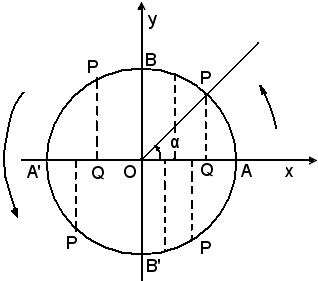
Si può quindi dire che il seno dell'angolo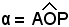
, come misura del segmento QP, andrà continuamente crescendo dal valore 0 al valore 1.
Quando poi l'angolo α continua a crescere da 90° a 180°, cioè quando il punto P, continuando nella sua rotazione, passa da B ad A' il segmento QP torna a decrescere dal valore OB al valore 0 e quindi il seno diminuisce continuamente dal valore 1 al valore 0.
Si continua a far crescere l'angolo α da 180° a 270°; il segmento QP torna a crescere, fino a diventare uguale al raggio OB' quando l'angolo è di 270°. Ma in questo caso la misura, cioè il seno, risulta negativa e quindi si può dire che, crescendo l'angolo da 180° a 270°, il seno decresce algebricamente dal valore 0 al valore -1.
Quando l'angolo α, sempre crescendo, passa da 270° a 360°, ed in tal caso P torna a coincidere con A, il segmento QP decresce dal valore OB' al valore zero, mentre la sua misura risulta ancora negativa; si può affermare perciò che il seno cresce dal valore -1 al valore 0.Concludendo,
si può dire quindi che, non solo i valori del seno risultano
sempre compresi tra -1 ed 1, ma che il seno assume tutti i valori
reali compresi tra questi estremi, nel senso che, scelto un qualsiasi
numero reale, in valore assoluto minore di 1, esiste sempre almeno un
angolo, compreso tra 0° e 360°, il cui seno è uguale a
quel numero fissato.
Analoghe considerazioni si possono ripetere per quanto riguarda la variazione del coseno, che rappresenta la misura, in valore assoluto e segno, del segmento OQ.
Si può quindi affermare che, quando l'angolo α cresce da 0° a 90°, il coseno diminuisce dal valore 1 al valore 0; quando l'angolo passa dal valore di 90° a quello di 180°, il coseno continua a decrescere dal valore 0 al valore -1, dopo di che, passando l'angolo da 180° a 270°, il coseno cresce, algebricamente, dal valore -1 al valore 0, infine quando l'angolo passa da 270° a 360°, il coseno passa dal valore 0 al valore 1.
Dai ragionamenti fatti, si traggono i seguenti risultati:
1)-il seno assume valori positivi nel I e nel II quadrante, negativi nel lII e nel IV ;
2)-il coseno assume valori positivi nel I e nel IV quadrante, negativi nel II e nel III ;
3)-il seno e il coseno hanno segni uguali nel I e nel III quadrante, contrari nel lI e nel IV;
4)-per l'angolo di 360° risulta
sen360° = sen0° = 0, cos360° = cos0° = 1.
Per comodità di consultazione, si riuniscono i primi risultati nella seguente tabella:
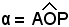Si suppone ora che il punto P, dopo aver compiuto un intero giro sul cerchio trigonometrico, continui la sua rotazione; l'arco e l'angolo diventeranno maggiori di 360°.
Qualunque sia però l'arco descritto dal punto P, e quindi corrispondentemente, qualunque sia l'angolo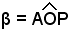 
, esisterà sempre un altro arco con gli stessi estremi del precedente, tale che il corrispondente angolo al centro 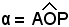risulti sempre compreso fra 0° e 360°; si può allora scrivere:
(2) senβ = senα, cosβ = cosα.
In altri termini, quando il punto mobile P, partendo dall'origine A degli archi arriva una prima volta in una certa posizione P e, successivamente, continua a girare sul cerchio, in un senso o nell'altro, fino a fermarsi di nuovo in P, dopo aver compiuto k giri, si può scrivere:
β = α + k360°
e risulta
(3) sen(α + k360°) = senα, cos(α + k360°) = cosα,
dove k indica un numero intero positivo o negativo qualsiasi.
Se poi si misurano gli angoli in radianti, le (3) assumono la forma
(3') sen(α + 2kπ) = senα, cos(α + 2kπ) = cosα.
Definizioni
1)-Una funzione f(x) si dice periodica di periodo T se, aumentando la variabile x di una quantità T, o di un multiplo qualsiasi di T, essa riprende lo stesso valore, cioè se risulta
f(x + kT) = f(x),
dove k è un numero intero arbitrario.
2)-Se aumentando la variabile x di metà del periodo, la funzione cambia di segno, cioè se
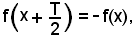
allora
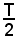
si chiama semiperiodo.
In base a queste definizioni, tenendo presenti le (3), si può enunciare la seguente proprietà:
-le funzioni circolari seno e coseno sono funzioni periodiche di periodo 360°, se si misurano gli angoli in gradi o di periodo 2π, se si misurano gli angoli in radianti.
Tangente
In riferimento al solito cerchio trigonometrico, sia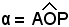 un qualsiasi angolo diverso da un angolo retto o da un multiplo dispari dell'angolo retto, cioè sia:
α ≠ 90° + k180°,
cioè
α ≠ (2k + 1)90°,
o anche
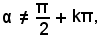
cioè
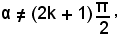
con k intero arbitrario positivo, negativo o nullo.
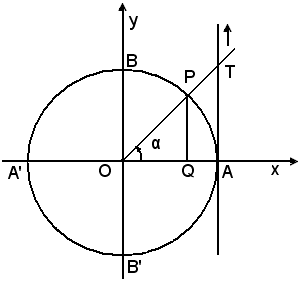
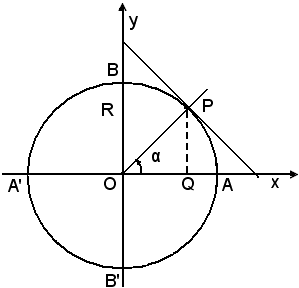
Nel punto A, origine degli archi, si conduce la tangente alla circonferenza e sia T la sua intersezione con il prolungamento del raggio OP.
Definizione - Si chiama tangente dell'angolo α, o dell'arco, e si indica con tgα,
il rapporto, in grandezza e segno, tra il segmento AT e il raggio OA,
cioè la misura rispetto al raggio del segmento AT di tangenza al
cerchio trigonometrico nel punto A.
Si ha quindi per definizione:
Si traccino da P le perpendicolari PQ e PR agli assi cartesiani, e si
considerino le misure dei segmenti orientati QP = OR e OQ, rispetto al
raggio OA della circonferenza, scelto come unità di misura,
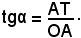
cioè si considerino i rapporti fra i segmenti orientati Si dimostra facilmente che questi rapporti non dipendono dalla particolare circonferenza di riferimento, ma solo dall'angolo al centro
corrispondente all'arco ; in altri termini sussiste il seguente teorema:-i due rapporti (1) dipendono solo dalla misura dell'arco
.Per dimostrare il teorema è sufficiente provare che, presi su due circonferenze diverse due archi
corrispondenti allo stesso angolo al centro, e quindi aventi la stessa
misura in radianti, i precedenti rapporti risultano uguali.A tale scopo, si considerano due circonferenze di centri O, O' e di raggi OA, O'A' e siano
due archi corrispondenti allo stesso angolo al centro ; tracciando da P e da P' le perpendicolari PQ e P'Q' ai raggi OA, O'A', si ottengono i
due triangoli rettangoli OQP, O'Q'P', che risultano simili tra loro per
avere gli angoli uguali ed allora i lati corrispondenti sono in
proporzione.Quindi, si può scrivere:
o anche, essendo OP = OA e O'P' = O'A',
come dovevasi dimostrare.
Questo teorema permette di affermare che i rapporti
-i due rapporti
si chiamano funzioni goniometriche dell'angolo α, oppure funzioni circolari dell'arco
.Queste funzioni si indicano con le scritture
senα, cosα,
e si leggono rispettivamente seno di α e coseno di α, sioè si pone per definizione:
Si osserva ora che le misure dei due segmenti orientati OQ e QP rappresentano rispettivamente l'ascissa e l'ordinata del generico punto P della circonferenza; allora, prendendo come unità di misura il suo raggio, si può enunciare la seguente proprietà:
-il coseno e il seno di un arco
rappresentano rispettivamente
l'ascissa e l'ordinata dell'estremo P dell'arco, in un sistema
cartesiano avente per assi i diametri tra loro ortogonali AA', BB' e
nel quale si assuma il raggio come unità di misura.Quando si assume come unità di misura delle lunghezze il raggio di una data circonferenza e si prendono come assi cartesiani due diametri fra loro ortogonali, la circonferenza stessa si chiama circonferenza o cerchio trigonometrico.
Pertanto, la precedente proprietà si può enunciare in modo più semplice.
-il coseno e il seno di un arco
del cerchio trigonometrico rappresentano rispettivamente l'ascissa e l'ordinata dell'estremo P dell'arco nel sistema cartesiano avente per asse delle x la retta individuata dal diametro OA, orientata da O verso A.Altra definizione di seno e coseno
Le due funzioni seno e coseno, appena definite mediante il cerchio trigonometrico, si possono definire anche direttamente, partendo da un angolo qualsiasi.
Infatti, considerato un angolo
,
si fissi un sistema di assi cartesiani ortogonali avente per origine il
vertice O dell'angolo e come semiasse positivo delle x il lato a.Si sceglie poi sull'altro lato b dell'angolo un punto P qualsiasi da cui si abbassa la perpendicolare PQ sul lato a e si considerano i due rapporti di segmenti orientati
Si vede facilmente che questi rapporti non dipendono dal particolare punto P scelto sul lato b, ma solo dall'angolo considerato.
Infatti, preso un qualsiasi altro punto P' su b, da questo si abbassa la perpendicolare P'Q' su a; i due triangoli rettangoli OQP OQ'P', così ottenuti, sono simili fra loro, perchè hanno l'angolo
in comune, pertanto i lati omologhi sono in proporzione, quindi si puo scrivereQP : OP = Q'P' : OP'; OQ : OP = OQ' : OP'
o anche
come dovevasi dimostrare.
I due rapporti
che dipendono solamente dalla misura dell'angolo
, si dicono rispettivamente seno e coseno dell'angolo α.Si dimostra ora che le funzioni così introdotte coincidono con le funzioni definite inizialmente.
Infatti, considerato l'angolo
, si costruisce la circonferenza di centro O e raggio OP, che incontra il lato a nel punto A.Si ottiene così l'arco orientato
, le cui funzioni circolari seno e coseno sono proprio i rapporti cioè sono le funzioni goniometriche dell'angolo α introdotte prima.
Per questa ragione le due funzioni seno e coseno si chiamano indifferentemente funzioni goniometriche, cioè misuratrici di un angolo, o funzioni circolari, o ciclometriche, cioè misuratrici di un arco.
Variazioni delle funzioni seno e coseno
Siccome il seno e il coseno di un angolo rappresentano le coordinate di un certo punto del cerchio trigonometrico, cerchio di raggio unitario, si può affermare che:
-in valore assoluto il seno e il coseno risultano sempre minori o uguali all'unità.
Inoltre, siccome le coordinate dei punti A e B del cerchio trigonometrico, sono A(1, 0), B(0, 1) e, quando il punto generico P coincide con A o con B, l'arco corrispondente
ha misura 0° oppure 90°, si puo scrivere:sen0° = 0, sen90° = 1, cos0° = 1, cos90° = 0.
Ragionando analogamente per i punti A' e B', le cui coordinate sono rispettivamente A'(-1, 0), B'(0, -1) ed osservando che quando il punto P coincide con A' o con B' l'arco corrispondente
ha per misura 180° oppure 270°, si puo scrivere:sen180° = 0, cos180° = -1, sen270° = -1, cos270° = 0.
Dopo questi primi risultati, si considera un arco
di
estremo P variabile in modo che il punto P, partendo dalla posizione
iniziale A, vi ritorni dopo aver compiuto un intero giro e,
corrispondentemente si considera il relativo angolo al centro α,
che varierà a sua volta da 0° a 360°.Quando l'angolo cresce da 0° a 90°, il segmento QP cresce continuamente fino a coincidere con il raggio OB.
Si può quindi dire che il seno dell'angolo
, come misura del segmento QP, andrà continuamente crescendo dal valore 0 al valore 1.Quando poi l'angolo α continua a crescere da 90° a 180°, cioè quando il punto P, continuando nella sua rotazione, passa da B ad A' il segmento QP torna a decrescere dal valore OB al valore 0 e quindi il seno diminuisce continuamente dal valore 1 al valore 0.
Si continua a far crescere l'angolo α da 180° a 270°; il segmento QP torna a crescere, fino a diventare uguale al raggio OB' quando l'angolo è di 270°. Ma in questo caso la misura, cioè il seno, risulta negativa e quindi si può dire che, crescendo l'angolo da 180° a 270°, il seno decresce algebricamente dal valore 0 al valore -1.
Quando l'angolo α, sempre crescendo, passa da 270° a 360°, ed in tal caso P torna a coincidere con A, il segmento QP decresce dal valore OB' al valore zero, mentre la sua misura risulta ancora negativa; si può affermare perciò che il seno cresce dal valore -1 al valore 0.
Analoghe considerazioni si possono ripetere per quanto riguarda la variazione del coseno, che rappresenta la misura, in valore assoluto e segno, del segmento OQ.
Si può quindi affermare che, quando l'angolo α cresce da 0° a 90°, il coseno diminuisce dal valore 1 al valore 0; quando l'angolo passa dal valore di 90° a quello di 180°, il coseno continua a decrescere dal valore 0 al valore -1, dopo di che, passando l'angolo da 180° a 270°, il coseno cresce, algebricamente, dal valore -1 al valore 0, infine quando l'angolo passa da 270° a 360°, il coseno passa dal valore 0 al valore 1.
Dai ragionamenti fatti, si traggono i seguenti risultati:
1)-il seno assume valori positivi nel I e nel II quadrante, negativi nel lII e nel IV ;
2)-il coseno assume valori positivi nel I e nel IV quadrante, negativi nel II e nel III ;
3)-il seno e il coseno hanno segni uguali nel I e nel III quadrante, contrari nel lI e nel IV;
4)-per l'angolo di 360° risulta
sen360° = sen0° = 0, cos360° = cos0° = 1.
Per comodità di consultazione, si riuniscono i primi risultati nella seguente tabella:
| Variazione del seno e del coseno | |||||
| Angolo | Seno | Coseno | Quadrante | Seno | Coseno |
| 0° o 360° | 0 | 1 | I | + | + |
| 90° | 1 | 0 | II | + | - |
| 180° | 0 | -1 | III | - | - |
| 270° | -1 | 0 | IV | - | + |
Si suppone ora che il punto P, dopo aver compiuto un intero giro sul cerchio trigonometrico, continui la sua rotazione; l'arco
e l'angolo diventeranno maggiori di 360°.Qualunque sia però l'arco
descritto dal punto P, e quindi corrispondentemente, qualunque sia l'angolo , esisterà sempre un altro arco con gli stessi estremi del precedente, tale che il corrispondente angolo al centro risulti sempre compreso fra 0° e 360°; si può allora scrivere:In altri termini, quando il punto mobile P, partendo dall'origine A degli archi arriva una prima volta in una certa posizione P e, successivamente, continua a girare sul cerchio, in un senso o nell'altro, fino a fermarsi di nuovo in P, dopo aver compiuto k giri, si può scrivere:
e risulta
(3) sen(α + k360°) = senα, cos(α + k360°) = cosα,
dove k indica un numero intero positivo o negativo qualsiasi.
Se poi si misurano gli angoli in radianti, le (3) assumono la forma
(3') sen(α + 2kπ) = senα, cos(α + 2kπ) = cosα.
Definizioni
1)-Una funzione f(x) si dice periodica di periodo T se, aumentando la variabile x di una quantità T, o di un multiplo qualsiasi di T, essa riprende lo stesso valore, cioè se risulta
f(x + kT) = f(x),
dove k è un numero intero arbitrario.
2)-Se aumentando la variabile x di metà del periodo, la funzione cambia di segno, cioè se
allora
si chiama semiperiodo.
In base a queste definizioni, tenendo presenti le (3), si può enunciare la seguente proprietà:
-le funzioni circolari seno e coseno sono funzioni periodiche di periodo 360°, se si misurano gli angoli in gradi o di periodo 2π, se si misurano gli angoli in radianti.
Tangente
In riferimento al solito cerchio trigonometrico, sia
un qualsiasi angolo diverso da un angolo retto o da un multiplo dispari dell'angolo retto, cioè sia:α ≠ 90° + k180°,
cioè
α ≠ (2k + 1)90°,
o anche
cioè
con k intero arbitrario positivo, negativo o nullo.
Nel punto A, origine degli archi, si conduce la tangente alla circonferenza e sia T la sua intersezione con il prolungamento del raggio OP.
Definizione - Si chiama tangente dell'angolo α, o dell'arco
, e si indica con tgα,
il rapporto, in grandezza e segno, tra il segmento AT e il raggio OA,
cioè la misura rispetto al raggio del segmento AT di tangenza al
cerchio trigonometrico nel punto A.Si ha quindi per definizione:
Nota bene
Nella definizione di tangente si è supposto che l'angolo α sia diverso dall'angolo retto o da un multiplo dispari dell'angolo retto, perchè altrimenti la semiretta OP, cadendo sulla semiretta OB, non incontrerebbe la tangente in A al cerchio trigonometrico.
In altri termini, per quanto detto, risulta che non esiste la tangente di un angolo retto o di un angolo multiplo dispari di un angolo retto. In seguito si vedrà come sia possibile togliere questa eccezione.
Espressione della tangente mediante seno e coseno
Si considerino i due triangoli rettangoli OQP e OAT della figura suddetta; essi sono simili perchè hanno in comune l'angolo α, quindi si può scrivere:
QP : OQ = AT : OA,
da cui, passando alle misure,
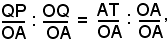
o anche, ricordando la definizione di seno e coseno,
senα : cosα = tgα : 1
e quindi, dividendo per cosα, è ciò è lecito perchè cosα ≠ 0, in quanto α ≠ (2k + 1)90°, si ha
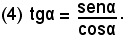
Si può allora enunciare la seguente proprietà:
-la tangente di un angolo, che non sia un multiplo dispari di un angolo retto, è uguale al rapporto tra il seno ed il coseno dello stesso angolo.
Cotangente
Si consideri ora un angolo qualsiasi α non nullo, che non sia miultiplo dell'angolo piatto, cioè si suppone che
α ≠ k180°,
oppure
α ≠ kπ;
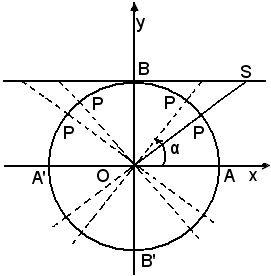
si conduce dal punto B la tangente al cerchio trigonometrico, che incontra in S il lato OP dell'angolo α.
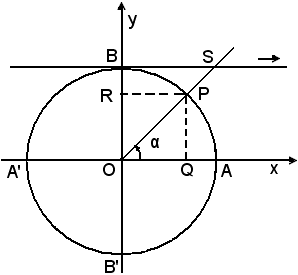
Definizione - Si chiama cotangente dell'angolo α, o dell'arco, e si indica con ctgα,
il rapporto, in grandezza e segno, tra il segmento BS e il raggio OA.
Si ha quindi per definizione:
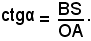
Nota bene
Nella definizione di cotangente si è supposto α ≠ k180°, perchè altrimenti la semiretta OP risulterebbe parallela alla tangente in B al cerchio trigonometrico e allora non esisterebbe l'intersezione S.
In altri termini, non esiste la cotangente di un angolo multiplo di un angolo piatto. In seguito si vedrà come sia possibile togliere questa eccezione.
Espressione della cotangente mediante seno e coseno
Si conduce da P la perpendicolare al diametro BB' e sia R il punto d'intersezione; i due triangoli rettangoli ORP, OBS sono simili perchè hanno in comune l'angolo
e quindi si può scrivere la proporzione
RP : OR = BS : OB,
o anche, siccome
RP = OQ, OR = QP, OB = OA,
OQ : QP = BS : OA,
da cui, passando alle misure, si ha
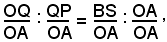
cioè, ricordando la definizione di seno e coseno,
cosα : senα = ctgα : 1,
e quindi dividendo per senα, è ciò è lecito perchè senα ≠ 0, in quanto α ≠ k180°, si ha
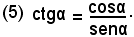
Si può allora enunciare la seguente proprietà:
-la cotangente di un angolo, che non sia un multiplo di un angolo piatto, è uguale al rapporto tra il coseno e il seno stesso angolo.
In generale, supponendo che l'angolo α non sia in multiplo, nè pari nè dispari, dell'angolo retto, in modo che esistano tgα e ctgα, dalle (4) e (5), si deduce:
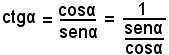
e quindi
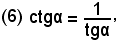
o anche
tgα·ctgα = 1.
Si deduce la seguente proprietà:
Variazioni delle funzioni tangente e cotangenteIn virtù delle formule (4) e (5), oppure dalle definizioni, si può scrivere:
tg0° = tg180° = 0; ctg90° = ctg270° =0.
Si suppone ora che l'angolo α cresca dal valore 0° al valore 90°; di conseguenza crescerà il segmento AT e quindi la sua misura rispetto al raggio, cioè la tangente.
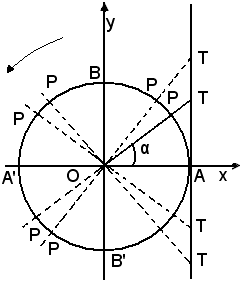
Si può dire inoltre che, comunque si scelga un numero m positivo, grande a piacere, esiste sempre un angolo sufficientemente vicino a 90°, tale che la sua tangente risulti maggiore del numero m.
Infatti, fissato m, si riporti, a partire da A sulla tangente al cercho trigonometrico, un segmento AM, la cui misura rispetto al raggio sia m, e si congiunga M con O.
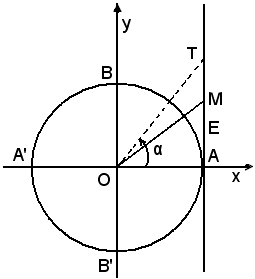
Si ottiene in tal modo l'angolo
, tale che 
; se si considera un qualsiasi angolo
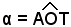maggiore di , la sua tangente, evidentemente, risulta maggiore di m, e ciò dimostra quanto asserito.
Si può quindi dire che:
-al crescere dell'angolo α da 0° a 90°, la sua tangente cresce indefinitamente e diventa e resta maggiore di un qualsiasi numero positivo prefissato, comunque grande.
Per esprimere ciò, si dice brevemente che:
-la tangente di un angolo tende all'infinito quando l'angolo tende a 90° o anche, meno esattamente, che la tangente di 90° è infinita.
Si fa ora crescere l'angolo da 90° a 180°; il punto P, nella figura precedente a quella suddetta, si troverà nel II quadrante e di conseguenza il lato OP incontrerà la tangente in A al cerchio trigonometrico in un punto appartenente al IV quadrante; la misura del segmento AT dovrà pertanto assumersi negativamente. D'altronde, se l'angolo α, sempre supposto maggiore di 90°, diminuisce continuamente avvicinandosi sempre più al valore di 90°, il punto T si allontana indefinitamente sulla tangente e quindi di nuovo la misura del segmento AT, in valore assoluto, tenderà all'infinito, nel senso spiegato in precedenza.
Tale circostanza si esprime dicendo che la tangente tende all'infinito negativo.
Concludendo, si può dire che l'angolo, avvicinandosi al valore di 90°, con valori crescenti, cioè per angoli appartenenti al I quadrante, la tangente tende all'infinito positivo, mentre quando l'angolo si avvicina al valore di 90°, con valori decrescenti, cioè per angoli appartenenti al II quadrante, la tangente tende all'infinito negativo.
Per esprimere tale proprietà, si usa la scrittura:
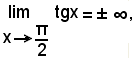
e si legge "limite di tangente x, per x che tende a π/2, uguale a più o meno infinito".
Continuando a far crescere l'angolo fino a 180°, il segmento AT diminuisce continuamente fino ad annullarsi, quando l'angolo diventa 180° si può dire che la tangente cresce algebricamente da meno infinito a zero.
Quando poi l'angolo passa da 180° a 270° la tangente torna, evidentemente, ad essere positiva, perchè dal punto T viene a trovarsi di nuovo nel I quadrante, anzi, assume tutti i valori positivi, da zero a più infinito, già assunti quando l'angolo variava da 0° a 90°.
Quest'ultima circostanza si esprime scrivendo:
(7) tg(α + 180°) = tgα.
dove α rappresenta un angolo qualsiasi del I quadrante.
Se l'angolo, contrinuando a crescere passa da 270° a 360°, la tangente torna ad essere negativa, riprendendo gli stessi valori che aveva assunto quando l'angolo apparteneva al II quadrante, così vale ancora la (7), e α indica un angolo del II quadrante.
Considerazioni del tutto analoghe si possono ripetere per la variazione della cotangente, per la quale sussiste la formula
(7') ctg(α + 180°) = ctgα.
Si deve però tenere presente che la cotangente cresce illimitatamente quando l'angolo si avvicina al valore 0° e al valore 180°.
Per comodità di consultazione, anche quest'ultimi risultati si riuniscono nella seguente tabella:
Nota bene
Ricordando la definizione di funzione periodica, le formule (7) e (7') permettono di affermare:
1)-le funzioni circolari tangente e cotangente sono funzioni periodiche di periodo 180° oppure π;
2)-le funzioni circolari tangente e cotangente sono sempre di segno concorde, come appare evidente da tgα·ctgα = 1;
3)-la positività, nel I e III quadrante e la negatività, nel I e III quadrante, della tangente e della cotangente, era prevedibile anche in virtù delle relazioni (4) e (5) esprimenti il valore di tgα e ctgα in funzione di seno e coseno, perchè seno e coseno sono concordi nel I e III quadrante, discordi nel II e IV.
Secante e cosecante
In alcune scienze applicate, specialmente in astronomia e topografia, spesso è utile considerare altre funzioni goniometriche.
In riferimento al solito cerchio trigonometrico, si consideri un angolo,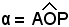
non multiplo di 90°; si conduca poi la tangente in P al cerchio
e si indichi con X, Y le sue intersezioni con gli assi x ed y.
Le misure dei due segmenti orientati OX, OY rispetto al raggio, cioè i due rapporti
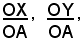
si dicono rispettivamente secante e cosecante dell'angolo α e si indicano con:
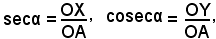
Si considerino ora i due triangoli rettangoli OQP, OXP, simili fra loro perchè hanno in comune l'angolo α, quindi si può scrivere la proporzione
OQ : OP = OP : OX,
o anche, essendo OP = OA,
OQ : OA = OA : OX.
Passando alle misure, segue
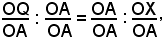
cioè, ricordando la definizione di coseno e di secante,
cosα : 1 = 1 : secα,
e quindi, essendo cosα ≠ 0, perchè per ipotesi α ≠ k90°,
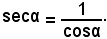
Analogamente, se si considerano gli altri due triangoli rettangoli OQP, OPY, simili fra loro perchè hanno in comune l'angolo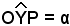
, quindi si può scrivere la proporzione
QP : OP = OP : OY,
o anche, essendo OP = OA,
QP : OA = OA : OY.
Passando alle misure, segue
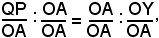
cioè, ricordando la definizione di seno e di cosecante,
senα : 1 = 1 : cosecα,
e quindi, essendo senα ≠ 0, perchè per ipotesi α ≠ k90°,
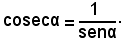
Variazioni delle funzioni secante e cosecante
Evidentemente la funzione cosecante resta definita da ogni valore dell'angolo α diverso da multipli di 180° e la funzione secante da ogni valore dell'angolo α diverso da multipli dispari di 90°.
Infatti, nel primo caso il secondo estremo P dell'arco
coincide con uno dei punti A, A', nel secondo con uno dei punti B, B';
la tangente al cerchio trigonometrico nel punto P risulta
rispettivamente parallela all'asse delle y o a quello delle x e di
conseguenza verrebbe a mancare uno dei punti Y o X.
Inotre, se si ripete lo stesso ragionamento fatto per la tangente, si può affermare che, quando l'angolo α tende a 0° o 180°, la cosecante tende all'infinito, positivo o negativo, mentre se l'angolo α tende a 90° o a 270°, la secante tende all'infinito, positivo o negativo.
Infine, le le due funzioni secante e cosecante, come per seno e coseno, risultano periodiche di periodo 360°, oppure 2π.
Nella definizione di tangente si è supposto che l'angolo α sia diverso dall'angolo retto o da un multiplo dispari dell'angolo retto, perchè altrimenti la semiretta OP, cadendo sulla semiretta OB, non incontrerebbe la tangente in A al cerchio trigonometrico.
In altri termini, per quanto detto, risulta che non esiste la tangente di un angolo retto o di un angolo multiplo dispari di un angolo retto. In seguito si vedrà come sia possibile togliere questa eccezione.
Espressione della tangente mediante seno e coseno
Si considerino i due triangoli rettangoli OQP e OAT della figura suddetta; essi sono simili perchè hanno in comune l'angolo α, quindi si può scrivere:
da cui, passando alle misure,
o anche, ricordando la definizione di seno e coseno,
senα : cosα = tgα : 1
e quindi, dividendo per cosα, è ciò è lecito perchè cosα ≠ 0, in quanto α ≠ (2k + 1)90°, si ha
Si può allora enunciare la seguente proprietà:
-la tangente di un angolo, che non sia un multiplo dispari di un angolo retto, è uguale al rapporto tra il seno ed il coseno dello stesso angolo.
Cotangente
Si consideri ora un angolo qualsiasi α non nullo, che non sia miultiplo dell'angolo piatto, cioè si suppone che
α ≠ k180°,
oppure
α ≠ kπ;
si conduce dal punto B la tangente al cerchio trigonometrico, che incontra in S il lato OP dell'angolo α.
Definizione - Si chiama cotangente dell'angolo α, o dell'arco
, e si indica con ctgα,
il rapporto, in grandezza e segno, tra il segmento BS e il raggio OA.Si ha quindi per definizione:
Nota bene
Nella definizione di cotangente si è supposto α ≠ k180°, perchè altrimenti la semiretta OP risulterebbe parallela alla tangente in B al cerchio trigonometrico e allora non esisterebbe l'intersezione S.
In altri termini, non esiste la cotangente di un angolo multiplo di un angolo piatto. In seguito si vedrà come sia possibile togliere questa eccezione.
Espressione della cotangente mediante seno e coseno
Si conduce da P la perpendicolare al diametro BB' e sia R il punto d'intersezione; i due triangoli rettangoli ORP, OBS sono simili perchè hanno in comune l'angolo
e quindi si può scrivere la proporzioneRP : OR = BS : OB,
o anche, siccome
RP = OQ, OR = QP, OB = OA,
OQ : QP = BS : OA,
da cui, passando alle misure, si ha
cioè, ricordando la definizione di seno e coseno,
e quindi dividendo per senα, è ciò è lecito perchè senα ≠ 0, in quanto α ≠ k180°, si ha
Si può allora enunciare la seguente proprietà:
-la cotangente di un angolo, che non sia un multiplo di un angolo piatto, è uguale al rapporto tra il coseno e il seno stesso angolo.
In generale, supponendo che l'angolo α non sia in multiplo, nè pari nè dispari, dell'angolo retto, in modo che esistano tgα e ctgα, dalle (4) e (5), si deduce:
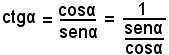
e quindi
o anche
tgα·ctgα = 1.
Si deduce la seguente proprietà:
-le funzioni circolari tangente e cotangente, nelle ipotesi indicate per l'angolo, sono l'una inversa dell'altra.
Variazioni delle funzioni tangente e cotangente
tg0° = tg180° = 0; ctg90° = ctg270° =0.
Si suppone ora che l'angolo α cresca dal valore 0° al valore 90°; di conseguenza crescerà il segmento AT e quindi la sua misura rispetto al raggio, cioè la tangente.
Si può dire inoltre che, comunque si scelga un numero m positivo, grande a piacere, esiste sempre un angolo sufficientemente vicino a 90°, tale che la sua tangente risulti maggiore del numero m.
Infatti, fissato m, si riporti, a partire da A sulla tangente al cercho trigonometrico, un segmento AM, la cui misura rispetto al raggio sia m, e si congiunga M con O.
Si ottiene in tal modo l'angolo
, tale che ; se si considera un qualsiasi angolo maggiore di , la sua tangente, evidentemente, risulta maggiore di m, e ciò dimostra quanto asserito.Si può quindi dire che:
-al crescere dell'angolo α da 0° a 90°, la sua tangente cresce indefinitamente e diventa e resta maggiore di un qualsiasi numero positivo prefissato, comunque grande.
Per esprimere ciò, si dice brevemente che:
-la tangente di un angolo tende all'infinito quando l'angolo tende a 90° o anche, meno esattamente, che la tangente di 90° è infinita.
Si fa ora crescere l'angolo da 90° a 180°; il punto P, nella figura precedente a quella suddetta, si troverà nel II quadrante e di conseguenza il lato OP incontrerà la tangente in A al cerchio trigonometrico in un punto appartenente al IV quadrante; la misura del segmento AT dovrà pertanto assumersi negativamente. D'altronde, se l'angolo α, sempre supposto maggiore di 90°, diminuisce continuamente avvicinandosi sempre più al valore di 90°, il punto T si allontana indefinitamente sulla tangente e quindi di nuovo la misura del segmento AT, in valore assoluto, tenderà all'infinito, nel senso spiegato in precedenza.
Tale circostanza si esprime dicendo che la tangente tende all'infinito negativo.
Concludendo, si può dire che l'angolo, avvicinandosi al valore di 90°, con valori crescenti, cioè per angoli appartenenti al I quadrante, la tangente tende all'infinito positivo, mentre quando l'angolo si avvicina al valore di 90°, con valori decrescenti, cioè per angoli appartenenti al II quadrante, la tangente tende all'infinito negativo.
Per esprimere tale proprietà, si usa la scrittura:
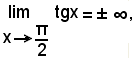
e si legge "limite di tangente x, per x che tende a π/2, uguale a più o meno infinito".
Continuando a far crescere l'angolo fino a 180°, il segmento AT diminuisce continuamente fino ad annullarsi, quando l'angolo diventa 180° si può dire che la tangente cresce algebricamente da meno infinito a zero.
Quando poi l'angolo passa da 180° a 270° la tangente torna, evidentemente, ad essere positiva, perchè dal punto T viene a trovarsi di nuovo nel I quadrante, anzi, assume tutti i valori positivi, da zero a più infinito, già assunti quando l'angolo variava da 0° a 90°.
Quest'ultima circostanza si esprime scrivendo:
(7) tg(α + 180°) = tgα.
dove α rappresenta un angolo qualsiasi del I quadrante.
Se l'angolo, contrinuando a crescere passa da 270° a 360°, la tangente torna ad essere negativa, riprendendo gli stessi valori che aveva assunto quando l'angolo apparteneva al II quadrante, così vale ancora la (7), e α indica un angolo del II quadrante.
Considerazioni del tutto analoghe si possono ripetere per la variazione della cotangente, per la quale sussiste la formula
(7') ctg(α + 180°) = ctgα.
Si deve però tenere presente che la cotangente cresce illimitatamente quando l'angolo si avvicina al valore 0° e al valore 180°.
Per comodità di consultazione, anche quest'ultimi risultati si riuniscono nella seguente tabella:
| Variazione della tangente e della cotangente | |||||
| Angolo | Tangente | Cotangente | Quadrante | Tangente | Cotangente |
| 0° | 0 | +∞ | I | + | + |
| 90° | ±∞ | 0 | II | - | - |
| 180° | 0 | ±∞ | III | + | + |
| 270° | ±∞ | 0 | IV | - | - |
| 360° | 0 | -∞ | - | ||
Ricordando la definizione di funzione periodica, le formule (7) e (7') permettono di affermare:
1)-le funzioni circolari tangente e cotangente sono funzioni periodiche di periodo 180° oppure π;
2)-le funzioni circolari tangente e cotangente sono sempre di segno concorde, come appare evidente da tgα·ctgα = 1;
3)-la positività, nel I e III quadrante e la negatività, nel I e III quadrante, della tangente e della cotangente, era prevedibile anche in virtù delle relazioni (4) e (5) esprimenti il valore di tgα e ctgα in funzione di seno e coseno, perchè seno e coseno sono concordi nel I e III quadrante, discordi nel II e IV.
Secante e cosecante
In alcune scienze applicate, specialmente in astronomia e topografia, spesso è utile considerare altre funzioni goniometriche.
In riferimento al solito cerchio trigonometrico, si consideri un angolo
,
non multiplo di 90°; si conduca poi la tangente in P al cerchio
e si indichi con X, Y le sue intersezioni con gli assi x ed y.Le misure dei due segmenti orientati OX, OY rispetto al raggio, cioè i due rapporti
si dicono rispettivamente secante e cosecante dell'angolo α e si indicano con:
Si considerino ora i due triangoli rettangoli OQP, OXP, simili fra loro perchè hanno in comune l'angolo α, quindi si può scrivere la proporzione
OQ : OP = OP : OX,
o anche, essendo OP = OA,
OQ : OA = OA : OX.
Passando alle misure, segue
cioè, ricordando la definizione di coseno e di secante,
cosα : 1 = 1 : secα,
e quindi, essendo cosα ≠ 0, perchè per ipotesi α ≠ k90°,
Analogamente, se si considerano gli altri due triangoli rettangoli OQP, OPY, simili fra loro perchè hanno in comune l'angolo
, quindi si può scrivere la proporzioneQP : OP = OP : OY,
o anche, essendo OP = OA,
QP : OA = OA : OY.
Passando alle misure, segue
cioè, ricordando la definizione di seno e di cosecante,
senα : 1 = 1 : cosecα,
e quindi, essendo senα ≠ 0, perchè per ipotesi α ≠ k90°,
Variazioni delle funzioni secante e cosecante
Evidentemente la funzione cosecante resta definita da ogni valore dell'angolo α diverso da multipli di 180° e la funzione secante da ogni valore dell'angolo α diverso da multipli dispari di 90°.
Infatti, nel primo caso il secondo estremo P dell'arco
coincide con uno dei punti A, A', nel secondo con uno dei punti B, B';
la tangente al cerchio trigonometrico nel punto P risulta
rispettivamente parallela all'asse delle y o a quello delle x e di
conseguenza verrebbe a mancare uno dei punti Y o X.Inotre, se si ripete lo stesso ragionamento fatto per la tangente, si può affermare che, quando l'angolo α tende a 0° o 180°, la cosecante tende all'infinito, positivo o negativo, mentre se l'angolo α tende a 90° o a 270°, la secante tende all'infinito, positivo o negativo.
Infine, le le due funzioni secante e cosecante, come per seno e coseno, risultano periodiche di periodo 360°, oppure 2π.