MIKY & GENNY
RELAZIONI FRA LE FUNZIONI GONIOMETRICHE ---> INDICE
Relazione fondamentale
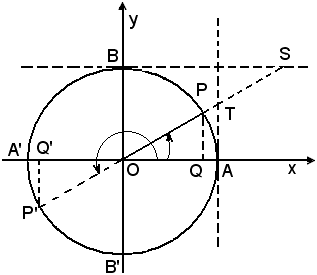
Nel cerchio trigonometrico si consideri un angolo qualsiasi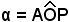
; applicando il teorema di Pitagora al triangolo rettangolo OHP, si può scrivere:
Q(OH) + Q(HP) = Q(OP),
ove con Q(OH), Q(HP) e Q(OP) sono stati indicati i quadrati dei lati OH, HP e OP.
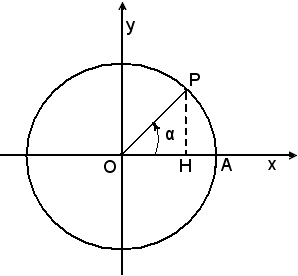
Passando alle misure, si ha:
Ricordando la definizione di seno e coseno, e osservato che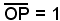
, dalla relazione precedente segue:
Se poi si tiene conto delle relazioni
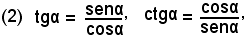
si può dire che:
-le quattro funzioni fondamentali della goniometria, seno, coseno, tangente e cotangente, non risultano fra loro indipendenti e tra esse sussistono le tre relazioni espresse da (1) e da (2).
Si deduce che, conoscendo una di queste funzioni, è possibile determinare i valori delle altre tre.
Espressioni delle funzioni goniometriche fondamentali quando è nota una di esse
1)-Dato il seno di un angolo, ci si propone di esprimere le altre tre funzioni legate ad esso.
Dalla (1) segue:
cos2α = 1 - sen2α,
da cui, estraendo la radice quadrata, si ha
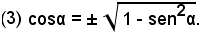
Sostituendo il valore della (3) nelle (2), si ottengono le formule:
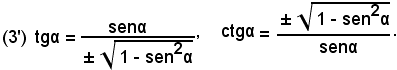
Nota bene
Nella (3) e di conseguenza nelle (3'), il doppio segno ±, si può eliminare solo se si conosce l'angolo α, oltre al seno, e quindi il quadrante a cui appartiene il secondo lato di α. Una semplice costruzione geometrica dimostra quanto detto.
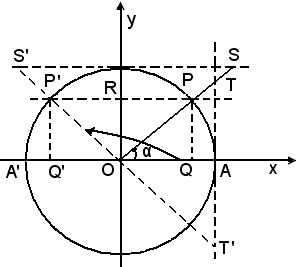
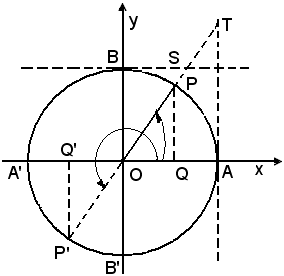
Infatti, assegnare il seno di un angolo significa, geometricamente, fissare il segmento OR dell'asse delle y, che individua i due angoli supplementari
aventi entrambi come seno la misura del segmento dato OR.
Le altre funzioni trigonometriche di questi due angoli supplementari rappresentano le misure dei segmenti orientati
OQ' = -OQ, AT' = -AT,
e quindi è naturale che tali misure risultano uguali fra loro e di segno contrario.
2)-Dato il coseno di un angolo, ci si propone di esprimere le altre tre funzioni, legate ad esso.
Dalla (1) segue:
sen2α = 1 - cos2α,
da cui, estraendo la radice quadrata, si ha
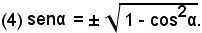
Sostituendo il valore della (4) nelle (2), si ottengono le formule
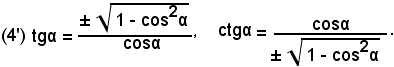
Nota bene
Nella (4) e di conseguenza nelle (4'), il doppio segno ±, si può eliminare solo se si conosce l'angolo α, oltre al coseno e quindi il quadrante a cui appartiene il secondo lato di α.
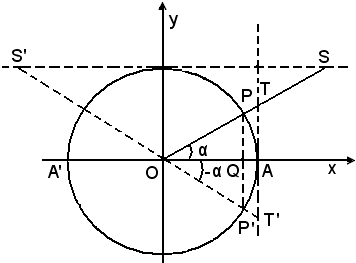
Geometricamente ci si rende conto di ciò, mediante un ragionamento analogo al precedente, osservando che, in tal caso, assegnare il coseno significa fissare il segmento OQ dell'asse delle x, al quale corrispondono i due angoli opposti
aventi entrambi per coseno la misura del segmento OQ. Tali angoli hanno
appunto seni, tangenti e cotangenti uguali e di segno contrario.
3)-Data la tangente di un angolo, ci si propone di esprimere le altre tre funzioni, legate ad essa.
Dalla seconda delle (2), si ha:
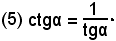
Se poi si considerano le altre due relazioni
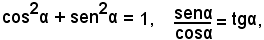
come un sistema di due equazioni algebriche nelle due incognite senα e cosα e lo si risolve con gli stessi procedimenti algebrici, si ottengono le espressioni per il seno ed il coseno.
Infatti, dalla seconda formula si ricava senα = cosα·tgα, e sostituendo tale valore del seno nella prima, si ha:
cos2α + cos2α·tg2α = 1,
o anche, mettendo in evidenza cos2α,
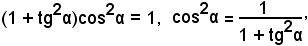
da cui, estraendo la radice quadrata, si ha
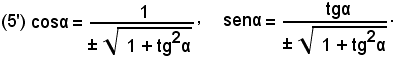
Nota bene
Anche in tal caso il doppio segno ± si può eliminare allo stesso modo dei casi precedenti.
Infatti, assegnare la tangente, significa fissare sulla tangente in A al cerchio trigonomrtrico il segmento AT, al quale corrispondono i due angoli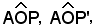 che differiscono di 180°.
Essi hanno entrambi per tangente la misura del segmento AT e per cotangente la misura del segmento BS, mentre hanno seni e coseni uguali e di segno contrario.
3)-Data la cotangente di un angolo, ci si propone di esprimere le altre tre funzioni, legate ad essa.
Dalla prima delle (2), si ha:
Se poi si considerano le altre due relazioni
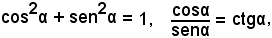
come un sistema di due equazioni algebriche nelle due incognite senα e cosα. e lo si risolve con gli stessi procedimenti algebrici, si ottengono le espressioni per il seno ed il coseno.
Infatti, dalla seconda formula si ricava cosα = senα·ctgα, e sostituendo tale valore del coseno nella prima, si ha:
sen2α + sen2α·ctg2α = 1,
o anche, mettendo in evidenza sen2α,
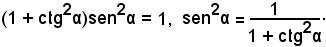
Estraendo la radice quadrata, si ha:
Nota bene
Per queste formule vale la stessa osservazione fatta in precedenza, per spiegare il doppio segno.
Infatti, assegnare la cotangente, significa fissare sulla tangente in B al cerchio trigonometrico il segmento BS, al quale corrispondono i due angoli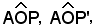 che differiscono di 180°.
Essi hanno entrambi per cotangente la misura del segmento BS e per tangente la misura del segmento AT; tali angoli hanno però seni e coseni opposti.
Nel cerchio trigonometrico si consideri un angolo qualsiasi
; applicando il teorema di Pitagora al triangolo rettangolo OHP, si può scrivere:Q(OH) + Q(HP) = Q(OP),
ove con Q(OH), Q(HP) e Q(OP) sono stati indicati i quadrati dei lati OH, HP e OP.
Ricordando la definizione di seno e coseno, e osservato che
, dalla relazione precedente segue:(1) cos2α + sen2α = 1,
che esprime il legame tra seno e coseno di un angolo qualsiasi.
La (1) si chiama relazione fondamentale della goniometria, quindi si può dire che:
-qualunque sia l'angolo, la somma dei quadrati del seno e del coseno è uguale all'unità.
che esprime il legame tra seno e coseno di un angolo qualsiasi.
La (1) si chiama relazione fondamentale della goniometria, quindi si può dire che:
-qualunque sia l'angolo, la somma dei quadrati del seno e del coseno è uguale all'unità.
Se poi si tiene conto delle relazioni
si può dire che:
-le quattro funzioni fondamentali della goniometria, seno, coseno, tangente e cotangente, non risultano fra loro indipendenti e tra esse sussistono le tre relazioni espresse da (1) e da (2).
Si deduce che, conoscendo una di queste funzioni, è possibile determinare i valori delle altre tre.
Espressioni delle funzioni goniometriche fondamentali quando è nota una di esse
1)-Dato il seno di un angolo, ci si propone di esprimere le altre tre funzioni legate ad esso.
Dalla (1) segue:
cos2α = 1 - sen2α,
da cui, estraendo la radice quadrata, si ha
Sostituendo il valore della (3) nelle (2), si ottengono le formule:
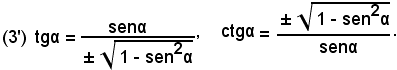
Nota bene
Nella (3) e di conseguenza nelle (3'), il doppio segno ±, si può eliminare solo se si conosce l'angolo α, oltre al seno, e quindi il quadrante a cui appartiene il secondo lato di α. Una semplice costruzione geometrica dimostra quanto detto.
Infatti, assegnare il seno di un angolo significa, geometricamente, fissare il segmento OR dell'asse delle y, che individua i due angoli supplementari
aventi entrambi come seno la misura del segmento dato OR.Le altre funzioni trigonometriche di questi due angoli supplementari rappresentano le misure dei segmenti orientati
OQ' = -OQ, AT' = -AT,
e quindi è naturale che tali misure risultano uguali fra loro e di segno contrario.
2)-Dato il coseno di un angolo, ci si propone di esprimere le altre tre funzioni, legate ad esso.
Dalla (1) segue:
sen2α = 1 - cos2α,
da cui, estraendo la radice quadrata, si ha
Sostituendo il valore della (4) nelle (2), si ottengono le formule
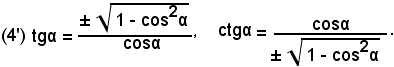
Nota bene
Nella (4) e di conseguenza nelle (4'), il doppio segno ±, si può eliminare solo se si conosce l'angolo α, oltre al coseno e quindi il quadrante a cui appartiene il secondo lato di α.
Geometricamente ci si rende conto di ciò, mediante un ragionamento analogo al precedente, osservando che, in tal caso, assegnare il coseno significa fissare il segmento OQ dell'asse delle x, al quale corrispondono i due angoli opposti
aventi entrambi per coseno la misura del segmento OQ. Tali angoli hanno
appunto seni, tangenti e cotangenti uguali e di segno contrario.3)-Data la tangente di un angolo, ci si propone di esprimere le altre tre funzioni, legate ad essa.
Dalla seconda delle (2), si ha:
Se poi si considerano le altre due relazioni
come un sistema di due equazioni algebriche nelle due incognite senα e cosα e lo si risolve con gli stessi procedimenti algebrici, si ottengono le espressioni per il seno ed il coseno.
Infatti, dalla seconda formula si ricava senα = cosα·tgα, e sostituendo tale valore del seno nella prima, si ha:
o anche, mettendo in evidenza cos2α,
da cui, estraendo la radice quadrata, si ha
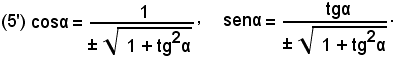
Nota bene
Anche in tal caso il doppio segno ± si può eliminare allo stesso modo dei casi precedenti.
Infatti, assegnare la tangente, significa fissare sulla tangente in A al cerchio trigonomrtrico il segmento AT, al quale corrispondono i due angoli
che differiscono di 180°.Essi hanno entrambi per tangente la misura del segmento AT e per cotangente la misura del segmento BS, mentre hanno seni e coseni uguali e di segno contrario.
3)-Data la cotangente di un angolo, ci si propone di esprimere le altre tre funzioni, legate ad essa.
Dalla prima delle (2), si ha:
Se poi si considerano le altre due relazioni
come un sistema di due equazioni algebriche nelle due incognite senα e cosα. e lo si risolve con gli stessi procedimenti algebrici, si ottengono le espressioni per il seno ed il coseno.
Infatti, dalla seconda formula si ricava cosα = senα·ctgα, e sostituendo tale valore del coseno nella prima, si ha:
o anche, mettendo in evidenza sen2α,
Estraendo la radice quadrata, si ha:
Nota bene
Per queste formule vale la stessa osservazione fatta in precedenza, per spiegare il doppio segno.
Infatti, assegnare la cotangente, significa fissare sulla tangente in B al cerchio trigonometrico il segmento BS, al quale corrispondono i due angoli
che differiscono di 180°.Essi hanno entrambi per cotangente la misura del segmento BS e per tangente la misura del segmento AT; tali angoli hanno però seni e coseni opposti.