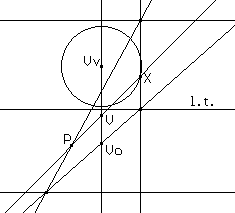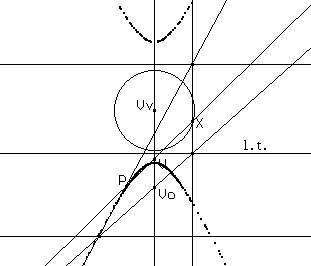
Metodi generali per il tracciamento di coniche
di Roberto Ricci
Vi sono diversi metodi per tracciare con Cabri particolari luoghi geometrici come ellissi, parabole, iperboli. Il lettore di questa rivista ne conosce senz'altro già alcuni. Qui si vogliono raccogliere e esaminare costruzioni in grado di generare indifferentemente sia ellissi, sia parabole, sia iperboli. Il lettore conosce già ad esempio il metodo generale per disegnare la conica passante per cinque punti dati, presentato nel n░3 di ottobre '94 dal prof. B.Scimemi e basato sul teorema di Steiner: un esagono semplice è inscritto in una conica se e solo se le tre coppie di lati opposti si tagliano in tre punti di una stessa retta.
Per realizzare una tale costruzione in Cabri potremo procedere ad esempio nel modo seguente:
creare i cinque punti base A, B, C, D ed E;
creare le rette AC e AD, le rette EB ed EC;
costruire l'intersezione N tra le rette AD ed EB;
costruire un punto K sulla retta EB;
creare la retta KD;
costruire l'intersezione M tra EC e KD;
creare la retta MN (su questa si tagliano le tre coppie di lati opposti della conica cercata);
costruire l'intersezione L tra MN ed AC;
costruire l'intersezione P tra DM e BL.

La conica è visualizzabile, selezionata l'opzione
Luogo di punti del menu Costruzioni, dopo aver indicato P e trascinando K lungo la retta EB.Naturalmente spostando i punti base A, B, C, D ed E potremo avere ad esempio il caso dell'ellisse, o dell'iperbole come nella figure seguenti.
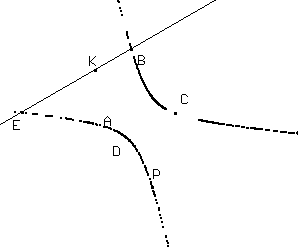
Per ottenere invece una parabola occorrerà trascinare il punto E, ad esempio, in modo che le rette BL e DK divengano parallele.
Ci si può anche servire direttamente di una definizione puramente proiettiva: una conica è il luogo di punti intersezione di rette corrispondenti in una proiettività tra due fasci.
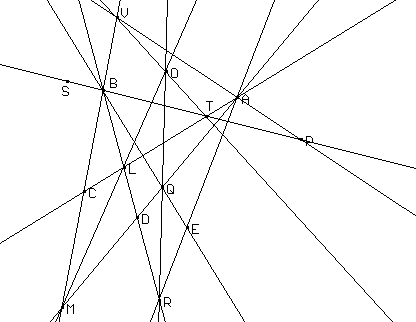
Per costruire una corrispondenza proiettiva tra due fasci ci si può servire del fatto che se r e r', s e s' sono rette corrispondenti allora la retta per i punti intersezione tra r e s' e tra r' e s, passa sempre per uno stesso punto detto centro di proiettività.
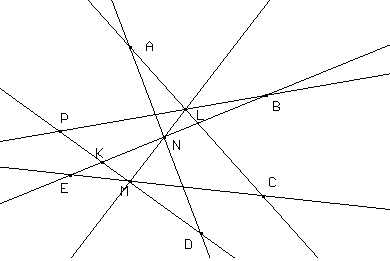
In Cabri, creati i centri A e B dei due fasci e date tre coppie di rette corrispondenti che si incontrano nei punti C, D e E, si può procedere nel modo seguente:
costruire il punto L intersezione tra AC e BD
costruire il punto M intersezione tra AD e BC
costruire il punto Q intersezione tra AD e BE
costruire il punto R intersezione tra AE e BD
costruire il punto O intersezione tra LM e QR
creare un punto S
costruire il punto T intersezione tra AC e BS
costruire il punto V intersezione tra OT e BC
costruire il punto P intersezione tra AV e BS
La conica è visualizzabile, selezionata l'opzione
Luogo di punti del menu Costruzioni, dopo aver indicato P e trascinando S nel piano intorno a B.Naturalmente spostando i punti base A, B, C, D ed E potremo avere ad esempio il caso dell'ellisse come nella figura seguente.
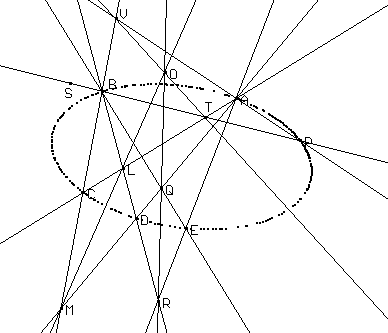
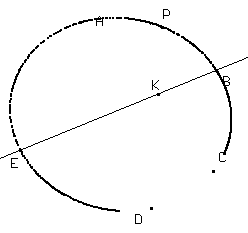
Ci potremo servire anche del fatto che ogni trasformazione proiettiva tra punti del piano trasforma circonferenze in coniche. Una trasformazione proiettiva tra punti del piano è determinata da quattro coppie di punti corrispondenti. Detti, ad esempio, A e A', B e B', C e C', D e D' le coppie di punti corrispondenti, per costruire il corrispondente P' di un punto P si può procedere nel modo seguente:
costruire il punto K intersezione di AC e BD
costruire il punto L intersezione di BD con PA
costruire il punto M intersezione di AC con PB
costruire il punto K' intersezione di A'C' e B'D'
costruire il punto L' tale che i punti B, K, L e D e i punti B', K', L' e D', nell'ordine, si corrispondano in una proiettività tra la retta AD e la retta A'D'
costruire il punto intersezione tra le rette BK' e B'K
costruire il punto intersezione tra le rette BD' e B'D
creare la retta per questi due punti
costruire il punto intersezione tra questa e le retta B'P
creare la retta per questo punto e per B
costruire il punto L' intersezione tra questa e la retta B'D'
costruire analogamente il punto M' sulla retta A'C'
costruire il punto P' intersezione di A'L' e B'M'
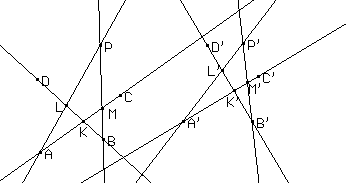
La conica è visualizzabile dopo aver creato una circonferenza e vincolato P a questa mediante l'opzione
Vincola un punto a un oggetto del menu Diversi, selezionando poi l'opzione Luogo di punti del menu Costruzioni, dopo aver indicato P', trascinando P lungo la circonferenza.Naturalmente spostando la circonferenza, o variandone il raggio, potremo avere ad esempio il caso dell'iperbole come nella figura seguente.
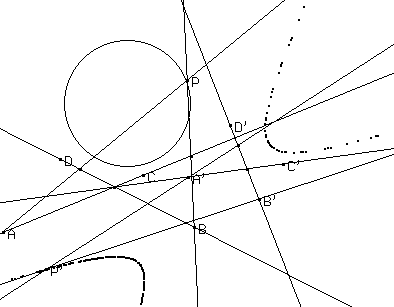
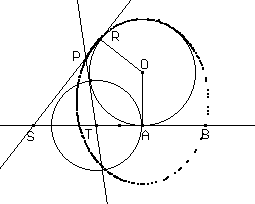
Un metodo particolarmente semplice per ottenere ellissi e iperboli è il seguente:
creare una circonferenza di centro O;
creare un punto qualunque A;
creare sulla circonferenza un punto S;
creare la retta OS;
costruire l'asse del segmento SA;
costruire il punto P intersezione tra l'asse e la retta OS.
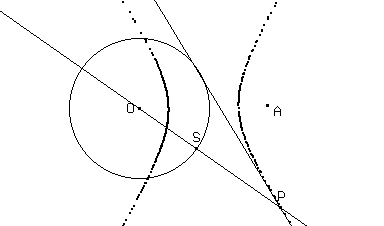
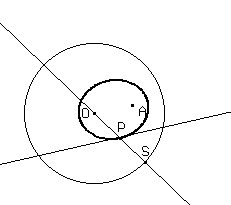
Ci si può rendere conto facilmente che il luogo dei punti P è, al variare di S sulla circonferenza, una conica osservando che da PS = PA deriva che |POPA| = OS quando OAOS oppure PO+PA=OS quando OA OS; dunque O e A sono inoltre i fuochi. L'osservazione suggerisce anche che non si otterrà mai una parabola.
Un'altra costruzione è descritta nel seguito
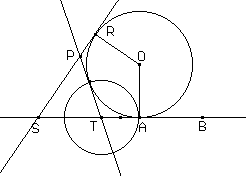
creare una circonferenza
costruire il centro O
costruire sulla circonferenza i punti A e R
costruire le rette tangenti alla circonferenza in A e in R
costruire l'intersezione T tra le due tangenti
costruire sulla tangente in A un punto B
costruire sulla tangente in A un punto S tale che il segmento ST sia congruente ad AB
costruire da T l'ulteriore tangente alla circonferenza
costruire l'intersezione P tra questa e la tangente alla circonferenza in R
Al variare di R il punto P descrive una conica. Se la lunghezza di AB è rispettivamente minore, uguale, maggiore del diametro della circonferenza, avremo rispettivamente un'iperbole, una parabola e un'ellisse.
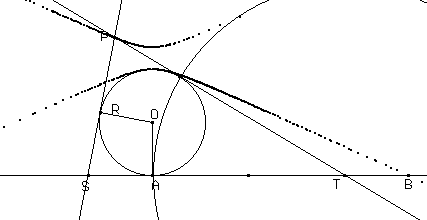
Si può realizzare inoltre una costruzione basata sul concetto di eccentricità, rapporto costante e tra la distanza del punto generico della conica da un punto F dato detto fuoco e una retta data r detta direttrice, PF = edist(P,r).
Con Cabri procerderemo ad esempio nel modo seguente:
creare il punto F e la retta d;
costruire la perpendicolare da F a d individuando il punto D;
costruire sul segmento FD il punto A;
creare la circonferenza di centro F e passante per A;
costruire il punto H sulla retta d;
costruire la circonferenza di centro H e raggio AD;
costruire la perpendicolare da H a d;
da uno dei due punti intersezione con la circonferenza di centro H costruire la parallela a FH;
costruire le intersezioni tra questa retta e la circonferenza di centro F;
creare le rette da F per questi due punti;
costruire le intersezioni tra queste due rette e la retta per H perpendicolare a d.
Il luogo descritto da P e Q al variare di H è appunto una conica.
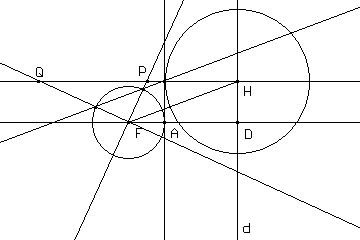
Possiamo dimostrare l'affermazione completando la figura con i punti R, S e T proiezioni sulla retta FH rispettivamente dei punti K, P e L e osservando che valgono le proporzioni PF/KF=PS/KR, PH/LH=PS/LT e che KR=LT e KF=FA, LH=AD.
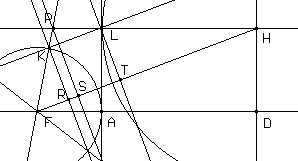
In Cabri si può visualizzare la conica selezionando l'opzione
Luogo di punti del menu Costruzioni, mantenendo premuto il tasto [Shift] mentre si indicano i punti P e Q e poi trascinando H lungo la direttrice.Un altro modo di procedere può prendere spunto dalla costruzione di due punti X e Y su una retta r in modo tale che il rapporto delle distanze da un punto D dato sulla retta r sia costante.
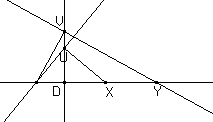
Potremo procedere costruendo la perpendicolare a r in D e costruendo su questa due punti V e U
....
Presa la retta r come asse focale e la perpendicolare ad essa in D come direttrice d, costruito il fuoco F sulla retta r, diviene semplice a questo punto creare il luogo dei punti P che hanno ditanze da F e da d in rapporto costante.
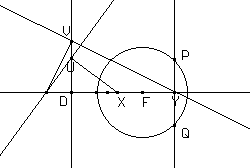
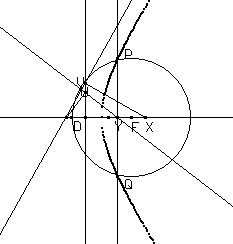
oppure, forse più semplicemente,
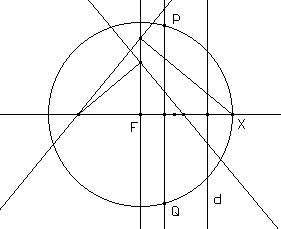
Potremo costruire coniche come trasformazioni ottico-geometriche di circonferenze, attraverso, ad esempio, lenti o specchi semplici. In particolare una lente semplice convergente si basa sulla costruzione seguente:
creare l'asse focale e su questo i punti O e F;
costruire la perpendicolare da O all'asse focale;
creare un punto P;
creare la retta OP;
costruire la parallela da P all'asse focale;
costruire l'uintersezione tra questa retta e la perpendicolare da O all'asse focale;
creare la retta per questo punto e per F;
costruire l'intersezione P' tra questa retta e la retta OP.
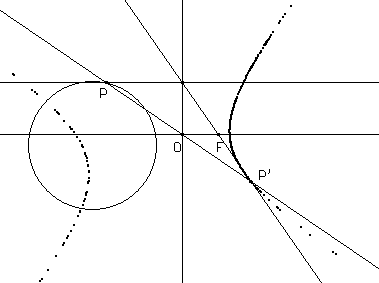
In particolare per circonferenze di centro in O si hanno i tre casi a seconda che F sia interno, sulla circonferenza o esterno.
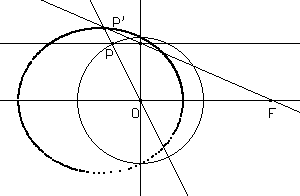
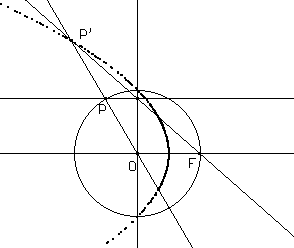
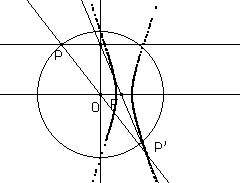
Per darsi una ragione del risultato basta osservare la figura seguente.
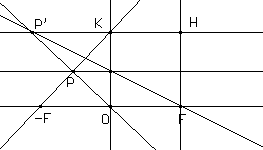
Essa mostra il raggio per P e F, che seguirà il cammino KH. Essendo dunque OH parallelo alla retta per F e K, il triangolo P'OH è simile al triangolo di vertici O, P e F, e quindi P'O/P'H = PO/OF; essendo PO costante quando P varia su una circonferenza di centro PO, il punto P' descrive una conica di fuoco F, direttrice FH e eccentricità PO/OF.
Infine potremmo ricondurci alla definizione di conica come sezione conica, sezione piana di un cono circolare retto indefinito. Si potrà ricorrere ad esempio a un metodo abbastanza naturale per rappresentare sul piano le tre dimensioni spaziali e costruire la conica come luogo dei punti intersezione di un piano parallelo alla l.t. con le rette VX essendo V il vertice del cono che ha sezione circolare sul piano verticale e V un punto di tale circonferenza.
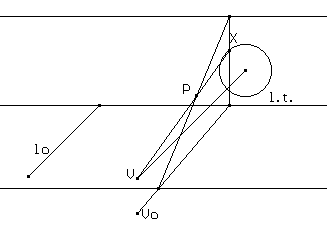
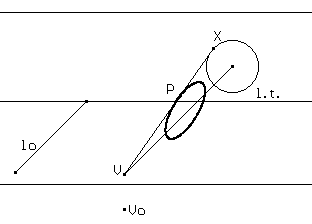
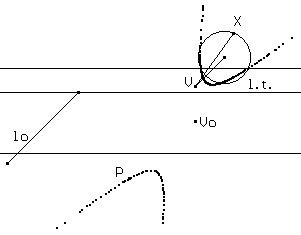
o anche con il metodo delle proiezioni ortogonali