2. Esempi di trasformazioni lineari
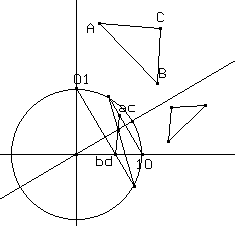
In ambiente Cabri, servendosi della macrocostruzione precedentemente descritta, si può operare concretamente su trasformazioni lineari, applicandole ad esempio a figure come triangoli. Si potrà studiare l'effetto di una data trasformazione lineare su figure diverse o anche su una stessa figura diversamente posizionata nel sistema coordinato; oppure si potrà studiare l'effetto su una stessa figura data di diverse trasformazioni lineari al fine, per esempio, di classificarle. In quest'ultimo caso sarà sufficiente trascinare i punti (a,c) e (b,d), che caratterizzano in modo univoco le trasformazioni lineari, siano essi liberi o vincolati su luoghi particolari o anche legati uno all'altro mediante una costruzione. Particolari tipi di trasformazioni lineari sono esaminati nel seguito. (a) L'identità si ottiene ovviamente quando i punti (a,c) e (b,d) si sovrappongono ai punti (1,0) e (0,1); sebbene l'esatta sovrapposizione di due punti, qui come più avanti, dia luogo a instabilità della costruzione, bisogna anche osservare che tale precisione è difficilmente realizzabile in pratica e che quindi tale instabilità non risulta evidente. (b) Le dilatazioni lungo l'asse x si ottengono (fig. 4) quando il punto (a,c) è vincolato sull'asse x, cioè (a,c) = (k,0), e il punto (b,d) si sovrappone a (0,1).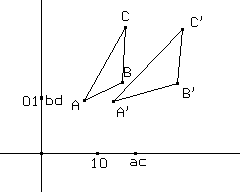 Analogamente le dilatazioni lungo l'asse y si ottengono quando (a,c) si sovrappone al punto (1,0) e il punto (b,d) è vincolato sull'asse y, cioè (b,d) = (0,k).
Infine le omotetie, cioè le dilatazioni della stessa ampiezza lungo entrambe le direzioni principali (fig. 5), si possono realizzare vincolando il punto (a,c) sull'asse x e sovrapponendo (b,d) al punto intersezione tra l'asse y e la parallela per (a,c) alla retta passante per i punti (1,0) e (0,1).
Analogamente le dilatazioni lungo l'asse y si ottengono quando (a,c) si sovrappone al punto (1,0) e il punto (b,d) è vincolato sull'asse y, cioè (b,d) = (0,k).
Infine le omotetie, cioè le dilatazioni della stessa ampiezza lungo entrambe le direzioni principali (fig. 5), si possono realizzare vincolando il punto (a,c) sull'asse x e sovrapponendo (b,d) al punto intersezione tra l'asse y e la parallela per (a,c) alla retta passante per i punti (1,0) e (0,1).
 (c) La simmetria di centro (0,0) si ottiene naturalmente sovrapponendo i punti (a,c) e (b,d) rispettivamente al simmetrico di (1,0) e al simmetrico di (0,1) rispetto a (0,0).
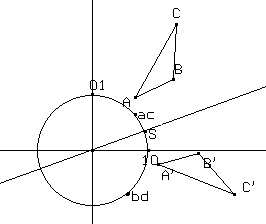
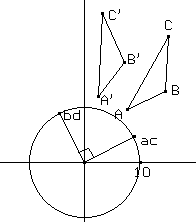
(d) Le simmetrie assiali con asse OS si ottengono, ad esempio al variare del punto S sulla circonferenza di centro in (0,0) e raggio unitario, costruendo (a,c) e (b,d) come simmetrici rispetto alla retta OS (fig. 6) dei punti (1,0) e (0,1).
(c) La simmetria di centro (0,0) si ottiene naturalmente sovrapponendo i punti (a,c) e (b,d) rispettivamente al simmetrico di (1,0) e al simmetrico di (0,1) rispetto a (0,0).
(d) Le simmetrie assiali con asse OS si ottengono, ad esempio al variare del punto S sulla circonferenza di centro in (0,0) e raggio unitario, costruendo (a,c) e (b,d) come simmetrici rispetto alla retta OS (fig. 6) dei punti (1,0) e (0,1).
 (e) Le rotazioni di centro O si ottengono ad esempio (fig. 7) vincolando il punto (a,c) sulla circonferenza di raggio unitario con centro in O e costruendo (b,d) come punto intersezione tra la stessa circonferenza e la retta passante per O e perpendicolare a quella per O e (a,c).
(e) Le rotazioni di centro O si ottengono ad esempio (fig. 7) vincolando il punto (a,c) sulla circonferenza di raggio unitario con centro in O e costruendo (b,d) come punto intersezione tra la stessa circonferenza e la retta passante per O e perpendicolare a quella per O e (a,c).
 Potrà essere di qualche interesse studiare anche famiglie continue di trasformazioni, ovvero le successive trasformazioni di una figura quando (a,c) varia su un luogo geometrico, a esempio una circonferenza, e (b,d) è costruito a partire da (a,c) e varia quindi di conseguenza.
Ad esempio:
(a) famiglia continua di omotetie con k che varia fra 1 e –1, da confrontare con la simmetria di centro O;
(b) famiglie continue di rotazioni (fig. 8) come movimento continuo nel piano quando (a,c) varia vincolato sulla circonferenza di centro O e raggio unitario;
Potrà essere di qualche interesse studiare anche famiglie continue di trasformazioni, ovvero le successive trasformazioni di una figura quando (a,c) varia su un luogo geometrico, a esempio una circonferenza, e (b,d) è costruito a partire da (a,c) e varia quindi di conseguenza.
Ad esempio:
(a) famiglia continua di omotetie con k che varia fra 1 e –1, da confrontare con la simmetria di centro O;
(b) famiglie continue di rotazioni (fig. 8) come movimento continuo nel piano quando (a,c) varia vincolato sulla circonferenza di centro O e raggio unitario;
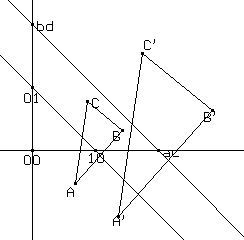
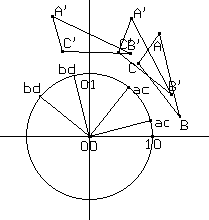 (c) famiglie continue di trasformazioni (fig. 9), che possono essere viste come rotazioni nello spazio intorno a un asse, quando (a,c) varia sul segmento che ha estremi in (1,0) e nel suo simmetrico (1,0)' rispetto all'asse dato, e (b,d) è l'intersezione del segmento che ha estremi in (0,1) e nel suo simmetrico (0,1)' rispetto all'asse dato con la retta passante per (a,c) e per il punto intersezione tra l'asse dato e il segmento di estremi (1,0)' e (0,1)'.
(c) famiglie continue di trasformazioni (fig. 9), che possono essere viste come rotazioni nello spazio intorno a un asse, quando (a,c) varia sul segmento che ha estremi in (1,0) e nel suo simmetrico (1,0)' rispetto all'asse dato, e (b,d) è l'intersezione del segmento che ha estremi in (0,1) e nel suo simmetrico (0,1)' rispetto all'asse dato con la retta passante per (a,c) e per il punto intersezione tra l'asse dato e il segmento di estremi (1,0)' e (0,1)'.