Aebly_proba

Il matematico svizzero Jakob Aebly (1885-1934) pubblicò nel 1923 la soluzione geometrica di un problema riguardante le probabibilità. In precedenza (1887-1888) lo stesso problema fu risolto e discusso anche da: J. Bertrand, É. Barbier,
D. André e venne ripreso anche da H. Poincaré nel "Calcul des Probabilités" (1912).

In un ballottaggio due candidati assistono allo spoglio delle schede. Un elettore ben informato è a conoscenza che il candidato A ha avuto m voti e il candidato B ne ha ottenuti n, con m > n.
Si chiede la probabilità che il candidato A sia sempre in vantaggio su B in tutti i risultati parziali dello scrutinio.

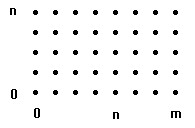Facciamo corrispondere all'insieme dei casi possibili una matrice di m + 1 per n + 1 punti come in figura. Per rappresentare i dati parziali dello scrutinio immaginamio dei percorsi che iniziano tutti dal punto (0,0) e terminano tutti nel punto (m,n). Per passare da un punto (i, j) al successivo sono ammesse soltanto due possibilità:


	oppure

Partendo (0,0) per arrivare in (m,n) si dovranno comunque effettuare m spostamenti verso destra e n spostamenti verso l'alto quindi il numero dei percorsi possibili è dato dal numero delle permutazioni di m + n oggetti dei quali m sono sono identici fra loro e n sono identici fra loro:

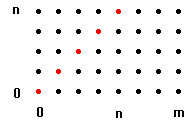
Se si chiede che il vincitore A sia sempre in vantaggio sul suo concorrente B allora l'insieme dei percorsi favorevoli è formato da tutti i percorsi che iniziano in (0,1) e non passano mai per i punti della diagonale segnati in rosso.
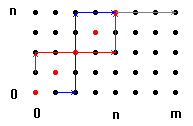
Osserviamo che i percorsi sfavorevoli invece iniziano tutti in (1,0), terminano tutti in (m,n), e passano per almeno un punto della diagonale segnata in rosso. Poiché ogni punto, quindi anche quelli della diagonale, possono essere raggiunti soltanto nei due modi fissati in precedenza allora ad ogni percorso sfavorevole che inizia (1,0) ne corrisponderà uno e uno soltanto, sempre sfavorevole, che inizia in (0,1) e che passa per gli stesi punti della diagonale del suo corrispondente. Ne risulta che il numero dei percorsi sfavorevoli è dato da

La probabilità richiesta è quindi