Argand

Di Jean-Robert Argand (1768-1822) non si conosce quasi nulla, dalle scarse notizie disponibili risulta nato in Svizzera a Ginevra e poi trasferitosi a Parigi dove svolse l’attività di “teneur de livres” (addetto alla tenuta dei libri contabili), verosimilmente presso la tipografia “Duminil-Lesueur, rue de la Harpe, 78”. Argand pubblicò nel 1806 un opuscolo dal titolo “Essai sur une manière de représenter les quantités imaginaires, dans les constructions géométriques”, il titolo è eloquente ed è per questo saggio sulla interpretazione geometrica dei numeri complessi che Argand viene ricordato.

Si conoscono alcuni scritti di Argand pubblicati negli anni 1813-1816 sugli “Annales de mathématiques pures et appliquées” comunemente noti come Annali di Gergonne; una rivista mensile pubblicata dal 1810 al 1832, prima a Nîmes poi a Montpellier, e diretta da Joseph-Diaz Gergonne (1771-1859).

La rivista aveva una sezione di problemi e noi prenderemo in esame due di questi problemi le cui soluzioni pubblicate sono le proposte inviate da Argand. Per semplicità riformuleremo i quesiti e non seguiremo alla lettera le soluzioni dell’Autore. Il materiale originale si può reperire all’indirizzo http://www.numdam.org/ . Per informazioni sugli "Annales" http://bibnum.cerimes.fr/

J-D Gergonne

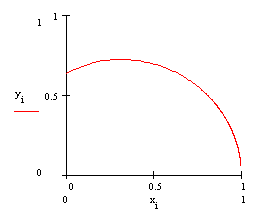
E’ data una circonferenza di raggio variabile r tangente in A ad una retta. Della circonferenza prendiamo gli archi di lunghezza fissata 2l che hanno in A il loro punto medio.
Determinare al variare de r il luogo M al quale appartengono gli estremi P e Q degli archi considerati.

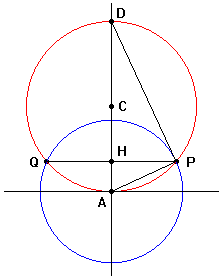
Fissiamo in A l’origine di un sistema di riferimento e tracciamo la circonferenza di raggio variabile r tangente in A all'asse delle ascisse.

Posto che PAQ = 2l, quindi PA = l, tenuto conto che l’arco PQ deve essere minore o uguale alla lunghezza della circonferenza di raggio variabile, ed esprimendo M in forma parametrica si ha

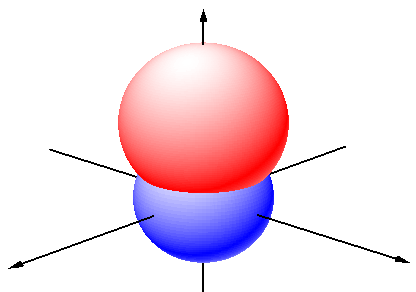
Per evidenti ragioni di simmetria ci si può limitare al grafico del luogo nel primo quadrante e ponendo per comodità l =1 si ha che

Il secondo problema è la versione tridimensionale del precedente.

E’ data una superficie sferica di raggio variabile r tangente in A ad un piano. Della superficie sferica consideriamo le calotte che hanno in A il loro polo e di area assegnata S.
Determinare al variare di r la superficie M alla quale appartengono le circonferenze delle calotte considerate.

Procediamo con una sezione ottenuta mediante un piano passante per A e per il centro della sfera e ponendo in A l’origine di un sistema d riferimento. L’area assegnata S della calotta sferica con polo in A deve essere minore o uguale alla superficie della sfera di raggio r quindi

inoltre

ne risulta che il luogo cercato è il luogo dei punti a distanza costante dal punto A cioè una superficie sferica centrata nell’origine di raggio