Catalan

Eugène Charles Catalan ( x 1833 ) 1814-1894

"Géomètre sans patrie, républicain sans République"

Dalla terza edizione (1858) del
- Théorèmes et problèmes de géométrie élémentaire -
del matematico franco-belga E.C. Catalan riprendiamo alcuni teoremi riguardanti i massimi e minimi geometrici.

T.1 - Tra tutti i triangoli aventi costante la somma di due lati e fissato l'angolo tra essi compreso quello di perimetro minimo è isoscele.

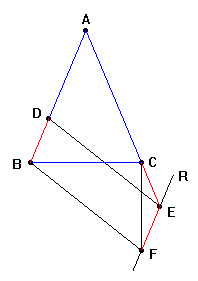
Se in un triangolo la somma di due lati è costante il perimetro è minimo quando è minima la lunghezza del terzo lato. Quindi preso il triangolo isoscele BAC, AB = AC, fissato l'angolo in A, preso su AB un punto D e sul prolungamento di AC un punto E tali che
DB = CE, per quanto detto sopra è sufficiente dimostrare che BC < DE.

Mandata per E una parallela a AB e per B una parallela a DE si ottiene il parallelogramma DBEF quindi BF = DE, inoltre il triangolo CEF è isoscele sulla base CF. Dato che la retta AB e la retta FR sono parallele allora gli angoli BAC e AER sono uguali. Ma l'angolo AER = 2 ECF e l'angolo BAC = 180 - 2 ACB quindi ACB + ECF = 90 e l'angolo BCF risulta retto; BF è ipotenusa del triangolo rettangolo BCF quindi BC < BF = DE.

T.2a - Determinare su una retta un punto tale che sia minima la somma delle distanze da due punti posti dalla stessa parte della retta data .

T.2b - Determinare su una retta un punto tale che sia massima la differenza delle distanze da due punti posti uno da una parte e uno da parte opposta della retta data .

Sia B' il simmetrico di B rispetto alla retta data. La retta AB' interseca la retta data in P e AP + PB è minima.
Infatti preso sulla retta data un punto M diverso da P nel triangolo AB'M si ha sempre

Sia A' il simmetrico di A rispetto alla retta data. La retta A'B interseca la retta data in P e AP - PB è massima.
Infatti preso sulla retta data un punto M diverso da P nel triangolo A'MB si ha sempre

T.3 - Inscrivere in un triangolo dato un triangolo di perimetro minimo.

Per ogni punto P del lato AB, in virtù di T.2, è sempre possibile trovare un triangolo inscritto di perimetro minimo: la retta passante per i punti P' e P'' simmetrici di P rispetto a BC e a CA interseca il triangolo ABC in due punti R e Q che insieme a P formano i tre vertici del triangolo inscritto di perimetro minimo e tale perimetro è rappresentato da P'P'''. Allora il problema consiste nel trovare, al variare di P su AB, il triangolo di minor perimetro. Per fare questo osserviamo che i simmetrici di P giacciono sempre sulle rette BP' e AP'' simmetriche di AB rispetto ai lati BC e CA. Le rette BP' e AP'' si intersecano in C' e al variare di P su AB la somma CP' + CP'' resta costante e pari al perimetro del triangolo ABC'. Allora per T.1 il terzo lato P'P'' del triangolo P''C'P' è minimo quando tale triangolo è isoscele. Quindi per costruire il triangolo cercato basta tracciare le rette BP' e AP'' simmetriche di AB rispetto ai lati BC e CA, e riportare su di esse C'P' = C'P'' uguali al semiperimetro del triangolo ABC'. Le intersezioni Q ed R di P'P'' con BC e CA danno due vertici del triangolo, il terzo vertice P è il simmetrico di P' rispetto a BC.

[ I punti P, Q, R sono i piedi delle altezze del triangolo ABC ]