Ernesto Cesàro
una proprietà di alcuni triangoli
    un problema di massimo
 
 

- Mathesis, tome neuvieme, année 1889 -

Nella soluzione di un quesito Ernesto Cesàro (1859-1906) ricorse ad una relazione esistente tra i lati di un triangolo nel quale uno degli angoli è doppio dell'altro.
Può essere utile soffermarsi sulla proprietà che utilizzò
« l'ingénieux analyste italien ».

 

Sia  ABC un triangolo isoscele sulla base AB. La bisettrice dell'angolo in B  taglia il lato opposto in D. Determinare la relazione che intercorre tra i lati del triangolo ABD.



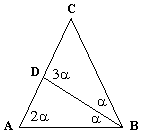Mediante i noti teoremi sui triangoli si ha immediatamente 

 

Ricavando il coseno dell'angolo alfa dalla prima relazione, sostituendo nella seconda ed utilizzando le identità trigonometriche si ottiene

.



 Con un procedimento analogo è possibile cercare una relazione anche tra le lunghezze dei lati del triangolo BCD nel quale un angolo è triplo dell'altro:

 

quindi          
Esistono triangoli isosceli i cui elementi hanno lunghezze in numeri interi che soddisfano a tutte le condizioni del problema. L'unico triangolo ABD  i cui lati hanno le lunghezze che formano una terna di numeri interi consecutivi è quello indicato in figura.

 

ERNESTO CESàRO
PROFESSORE ORDINARIO DELLA R. UNIVERSITà DI NAPOLI

ELEMENTI DI CALCOLO INFINITESIMALE

NAPOLI

LORENZO ALVANO LIBRAIO-EDITORE, Via università, 26
 1905
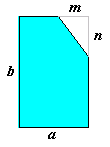
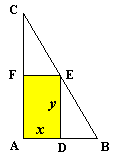
 Problema
«Prendiamo una lastra rettangolare, rotta ad un angolo nel modo indicato in figura, e proponiamoci di ricavarne un'altra lastra rettangolare, la cui area sia massima. È naturale conservare nella nuova lastra i due lati rimasti intatti ...»
Ricordiamo che il rettangolo di area massima inscritto in un triangolo rettangolo ha i lati che sono la metà dei cateti del triangolo. Dalla similitudine dei triangoli ABC e DBE si ha che
quindi l'area è massima quando
 
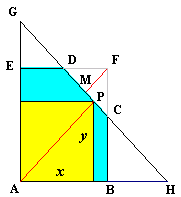
Scelto un sistema di riferimento avente gli assi solidali con i lati della lastra rimasti intatti e posto: AB = a, AE = b, DF = m, FC = n  si ha che i punti C e D hanno coordinate
. E la retta passante per C e D che ha equazione

stacca sugli assi due segmenti di lunghezza
L'area massima si ha quando  

quindi per

Chiamato con M il punto medio del segmento DC poiché il rapporto

risulta che il segmento MF e la diagonale AP del rettangolo di area massima sono paralleli. Quindi per tracciare il rettangolo di area massima si congiunge F con il punto medio M di DC quindi si manda la parallela a MF passante per A che interseca in P la retta HG ; se P cade esternamente a DC basta prendere l'estremo più vicino del segmento.