Cilindro_max

Il contenuto di questa pagina trae liberamente spunto dall'articolo del Prof. Lenthéric pubblicato sugli Annali di Gergonne nel 1829. L'articolo è reperibile all'indirizzo

http://www.numdam.org/item?id=AMPA_1829-1830__20__183_1

I risultati proposti sugli Annali vennero riportati anche nel Bollettino di Férussac del 1830. Fu tramite il Bollettino che queste tesi giunsero all'attenzione del Prof. Giusto Bellavitis che, nel fornirne una dimostrazione puramente geometrica, ebbe modo di confutare una delle conclusioni proposte dal collega francese. Lo scritto di Bellavitis fu pubblicato sugli Annali delle scienze del Regno Lombardo-Veneto, Padova, 1831, p. 406-407. Alcuni frammenti di questi scritti sono riportati in fondo alla pagina.

Il problema si focalizza sulle proprietà di massimo che assumono alcune grandezze le aree della superficie laterale, della superficie totale e il volume un cilindro circolare retto inscritto in una sfera di raggio r.

Posti

la superficie laterale del cilindro inscritto è data da

Osserviamo che l'area della superficie laterale è massima quando è massima l'area del triangolo rettangolo OAB la cui ipotenusa è costante e vale r. Questo consente di arrivare immediatamente al risultato ma, per mantenere omogeneità con i casi successivi, preferiamo continuare con lo studio della funzione

Questa funzione ha come dominio naturale [-r, r] ma ci interessa soltanto il grafico nel primo quadrante. Il grafico che si vede a sinistra è quello per r = 1. Studiando la derivata prima si arriva a dire che la funzione ammette massimo per

cioè quando l'altezza h del cilindro corrisponde al lato del quadrato inscritto nel cerchio massimo della sfera (e il triangolo rettangolo OAB è isoscele cioè la metà di un quadrato). L'area della superficie laterale del cilindro in questo caso vale

ed è due volte l'area del cerchio massimo.

Per tradurre il problema in un modello geometrico, a meno di una costante moltiplicativa, possiamo interpretare il sistema delle due equazioni come il massimo valore della coordinata z che può assumere una curva sghemba ottenuta dalla intersezione di due superfici tridimensionali.

Cioè di un paraboloide iperbolico con la superficie di un cilindro circolare retto.

e otteniamo così che

L'equazione del volume di fatto è una cubica il cui dominio naturale va ristretto, per motivi geometrici, al semiasse positivo delle ascisse cioè allo studio del suo grafico nel primo quadrante. Come nel caso precedente il grafico a sinistra è ottenuto ponendo r = 1. Studiando questa funzione si ha un massimo per

e il volume massimo vale

Traduciamo il problema in un modello geometrico. A meno di una costante moltiplicativa, possiamo interpretare il sistema delle due equazioni come il massimo valore assunto dalla coordinata z di una curva sghemba ottenuta dalla intersezione di due superfici tridimensionali.

Ancora con le stesse convenzioni della figura iniziale cerchiamo la superficie totale massima del solito cilindro circolare retto inscritto nella sfera di raggio r. In questo problema si ha la discordanza tra i risultati di Bellavitis e quelli di Lenthéric. Ancora

da cui segue

La funzione ha come dominio naturale [-r, r] ma ci interessa soltanto il grafico nel primo quadrante. Il grafico che si vede a sin9istra è quello ottenuto per r = 1. Lo studio della derivata prima di questa funzione conduce alla soluzione di un'equazione biquadratica. Dall'insieme delle quattro radici reali e distinte è possibile isolare quella geometricamente accettabile e concludere che la funzione ammette un massimo in

Traducendo il problema in un modello geometrico, a meno di una costante moltiplicativa, possiamo interpretare la soluzione del sistema delle due equazioni ottenute come il massimo valore assunto dalla coordinata z di una curva sghemba ottenuta dalla intersezione di due superfici tridimensionali.

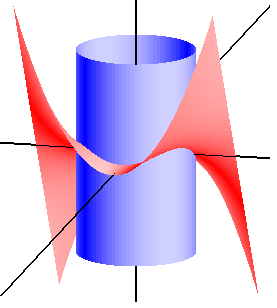
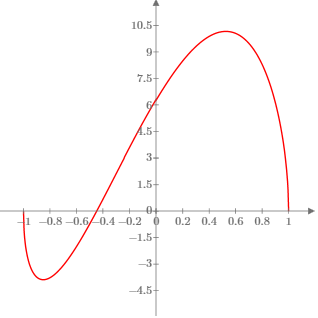
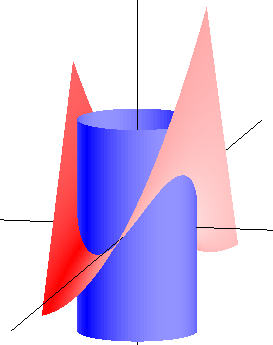
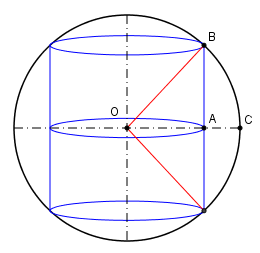
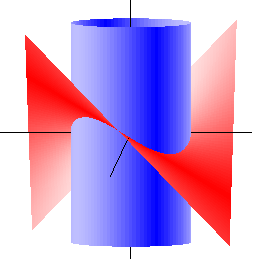
Adesso veniamo al contrasto tra i risultati di Lenthéric e quelli di Bellavitis. Bellavitis procede per via puramente geometrica dimostra l'esistenza del cilindro di superficie totale massima e che, in questo caso,

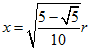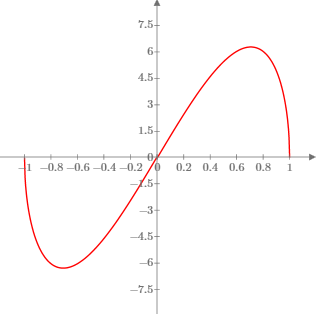
Lenthéric procede per via analitica come abbiamo fatto anche noi. Studiando la derivata prima della funzione che esprime l'area della superficie totale si arriva all'equazione

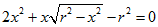e da questa all'equazione biquadratica

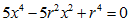che ammette quattro radici reali e distinte ma l'unica che rappresenta un massimo del problema è data proprio da

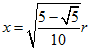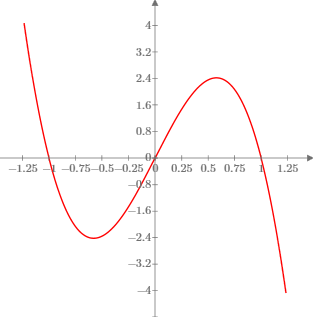
Al contrario Lenthéric afferma che il problema della ricerca del massimo non ammette propriamente una soluzione perché lo studio dell'equazione che esprime la derivata prima della funzione ha come radici

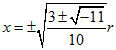cioè non ammette radici reali. In effetti però queste quattro radici sono le soluzione dell'equazione biquadratica

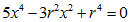che non è quella corretta. In sostanza Lenthéric nel determinare il termine di secondo grado di questa equazione, che risulta dalla somma di alcuni termini simili, ha commesso un banale errore di calcolo, probabilmente una svista nel valutare il segno di qualche addendo.