Adriaan Metius

  
 

Pi ~ 355/113

  
 
L'olandese Adriaan Metius (Alkmaar 1571 - Franeker 1635) utilizzando i risultati ottenuti dal padre, ottenuti con metodi archimedei, arrivò a stabilire che il numero razionale 355/113 è un'ottima approssimazione di Pi greco.
In effetti 355/113 = 3,141593 ... mentre Pi = 3,141592 ...
Presenteremo due costruzioni geometriche che, fissato un segmento unitario, permettono di determinare un segmento la cui lunghezza e' esattamente 355/113.
 
Iniziamo dalla costruzione proposta dall'olandese Jakob de Gelder (Rotterdam 1765 - Leiden 1848). La costruzione geometrica sfrutta alcune delle proprietà degli interi contenuti nella frazione di Metius e, in particolare, sulla determinazione esatta della parte decimale del rapporto 355/113.
Si osserva che

Data una circonferenza di centro O e raggio OA = 1. Sul raggio OB ortogonale a OA prendiamo un punto C tale che OC = 7/8. Sul segmento CA prendiamo un punto D tale che DA = 1/2. Da D mandiamo la normale a OA e sia E il piede della perpendicolare. La parallela a CE passante per D taglia OA in F. La lunghezza del segmento FA vale 16/113.
Il triangolo COA è rettangolo in O quindi

I triangoli rettangoli COA e DEA sono simili

Anche i triangoli  e  sono simili

Nell'ultima relazione sostituendo i risultati delle due precedenti si ottiene

 
La seconda costruzione si trova sul testo di geometria del 1857 dello statunitense George R. Perkins insegnante di matematica a Utica NY.
 
Con la costruzione geometrica proposta da Perkins non si arriva ad un segmento di lunghezza 355/113 ma si determinano due segmenti ed il rapporto delle loro lunghezze dà il numero razionale richiesto.
Rivisiteremo la costruzione per avere il rapporto in una forma più generale e da questa trarre il caso particolare che ci interessa.
 
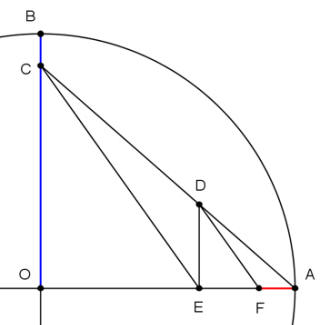
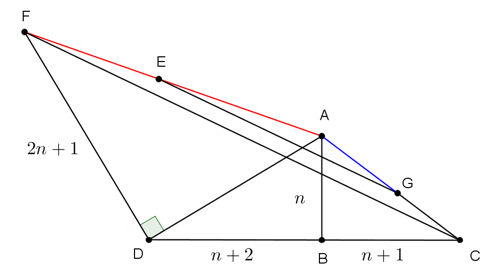
Consideriamo il triangolo ADC avente la base DC e l'altezza AB le cui lunghezze sono espresse da numeri interi interi.
Mandata per D una retta ortogonale ad AD, dalla stessa parte di A rispetto alla base DC prendiamo un segmento DF di lunghezza intera.

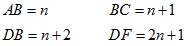Su AF prendiamo un punto E tale che AE = AC e per E mandiamo la parallela ad FC che interseca AC in G.
 Ci interessa il rapporto AF/AG.
Dalla similitudine dei triangoli EAG e FAC si ha

quindi

Utilizzando le lunghezze dei segmenti, applicando il Teorema di Pitagora sui triangoli rettangoli della figura, risulta

che per n = 7 diventa