Charles Dupin
	percorsi più convenienti

Charles Dupin 1784-1873

Pierre Charles François Dupin  fu matematico e uomo politico; allievo della  École Polytechnique (x 1801), fu discepolo di Monge, e venne nominato barone da Luigi XVIII nel 1824. I suoi lavori attengono alla geometria differenziale, ingegneria civile e navale.

Dalla raccolta di memorie "Applications de géométrie et de méchanique a la marine, aux ponts et chaussées, etc." (1822) riprendiamo alcune semplici applicazioni della geometria alla soluzione di problemi di trasporto.

T1. In ogni quadrilatero convesso la somma dei lati opposti è minore della somma delle diagonali.

Sia O il punto di intersezione delle diagonali. Applicando la disuguaglianza triangolare ai triangoli AOB e COD e sommando si ottiene

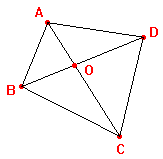
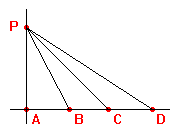
Applichiamo il teorema ad un sistema di trasporti con 3 punti di distribuzione: A, B, C, e tre punti di consegna:  A', B', C', dove i punti di partenza e i punti di arrivo delle merci appartengono rispettivamente a due rette distinte. Ogni punto di destinazione può essere rifornito da uno e uno soltanto dei punti di distribuzione, quale non importa. Lo scopo è quello di determinare i collegamenti in modo tale che la lunghezza complessiva, quindi il costo, dei trasporti risulti minima.

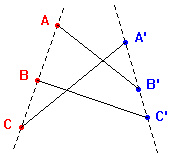
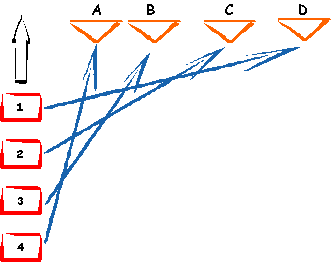
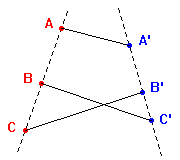
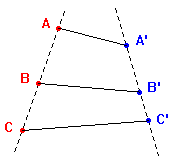
Iniziamo da una rete (la prima a sinistra) in cui sono presenti degli incroci. Applicando il T1 al quadrilatero AA'B'C si ottiene una rete, ancora con un incrocio ma di lunghezza totale inferiore alla precedente. Di nuovo applicando T1 al quadrilatero AB'C'C si ottiene l'ultima rete a destra, priva di incroci, che è quella di lunghezza minima cercata.

Diversa è la situazione se si chiede che il tempo complessivo del trasporto risulti minimo, in questo caso gli incroci tra i percorsi sono inevitabili se non necessari. Prendiamo ad esempio i percorsi che dovranno effettuare quattro plotoni di soldati che si muovono in colonna e che ricevono l'ordine di schierarsi in linea su delle posizioni assegnate lungo una retta ortogonale a quella di marcia. Perchè tutta la manovra avvenga in un tempo minimo è necessario che il plotone di coda (il più lontano dalle posizioni da raggiungere) compia un tragitto di lunghezza minima, a scalare lo stesso criterio dovrà essere applicato alle restanti unità.

Per valutare le distanza è sufficiente rifarsi ad un noto teorema di geometria illustrato a sinistra dove si ha PA < PB < PC < PD .

Sulla base di queste considerazioni si arriva allo schema riportato sotto. L'animazione mostra, a intervalli regolari di tempo, le posizioni dei singoli plotoni che si muovono tutti alla stessa velocità.