Duplicazione

Presentiamo tre costruzioni geometriche che rappresentano altrettante soluzioni approssimate del problema della duplicazione del cubo. In sostanza dato un segmento si tratta di determinarne un secondo la cui lunghezza sia pari a quella del segmento iniziale moltiplicata per la radice cubica di due. In questo modo se il cubo che ha per spigolo il primo segmento ha un volume V allora il cubo che ha per spigolo il secondo segmento ha un volume 2V. Il problema non ammette soluzione con riga e compasso da cui segue la ricerca di soluzioni approssimate con costruzioni più o meno complesse e scarti più o meno sensibili dal valore teorico.

La prima costruzione che presentiamo comparve nel 1825 sugli Annales de Mathématiques pures et appliquées. La riproporremo con alcune modifiche che non ne alterano il senso complessivo.

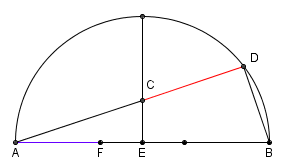
Dato il segmento AB = 3AF = 3a tracciamo la circonferenza che ha AB come diametro, quindi raggio AE = EB = 3a/2. Mandiamo per il centro E della circonferenza il raggio ortogonale ad AB e su di esso riportiamo un segmento EC = EF = a/2. La retta AC taglia la circonferenza in D ed il segmento CD è la soluzione del problema nel senso che CD è una buona approssimazione di AF moltiplicato per la radice cubica di due.

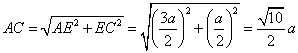Dalla similitudine dei triangoli rettangoli ACE e ADB si ricava

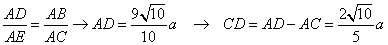Posto che a sia unitario si ottiene uno scarto

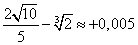e la costruzione fornisce un'approssimazione per eccesso rispetto al valore teorico.

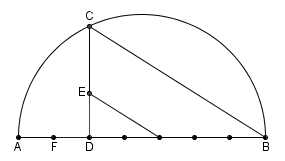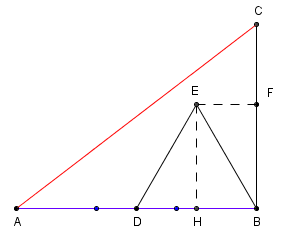
Per ottenere lo stesso risultato si può utilizzare anche una costruzione più semplice. Presi due segmenti consecutivi AD = 2a e DB = 5a tracciamo la semicirconferenza di diametro AB. Per D mandiamo la perpendicolare ad AB che taglia la semicirconferenza in C. Per il T. di Euclide si ha

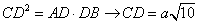Unito C con B mandiamo la parallela a CB passante il punto posto ad una distanza di 2a da D. Per la similitudine tra i due triangoli rettangoli che si sono formati si ha

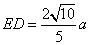Passiamo ad una costruzione del 1876 di Gaetano Buonafalce. Dato un quadrato ABCD sul lato BC = a prendiamo un segmento CF = EC che è 1/6 della diagonale AC del quadrato. Il segmento AF è una buona approssimazione di AB per la radice cubica di due.

Dal teorema di Pitagora sul triangolo rettangolo ABF si ricava

e posto il lato del quadrato come unitario si ottiene

dunque una approssimazione per difetto migliore della precedente.

L'ultima costruzione si trova in una comunicazione del Prof. George Gabriel Stokes, relativa ad un articolo di William Hayden, pubblicata sui Proceeding of the Royal Society of London del 1872. Come al solito la riprendiamo con delle modifiche minime che mirano a ridurre lo spazio di presentazione.

Dato il segmento AB sia D il suo punto medio. Costruiamo il triangolo equilatero DBE di base DB. Mandiamo per B la perpendicolare ad AB e su di essa riportiamo: un segmento BF di lunghezza pari all'altezza del triangolo equilatero DBE e il segmento FC di lunghezza pari a 1/3 di AB. Si forma in questo modo il triangolo rettangolo ABC la cui ipotenusa AC è una buona approssimazione di AB per la radice cubica di due.

Posto AB = a = 1 si ottiene uno scarto

dunque ancora un'approssimazione per difetto ma decisamente migliore delle due precedenti.