 |
|
|
|
 |
|
 |
 |
|
|
|
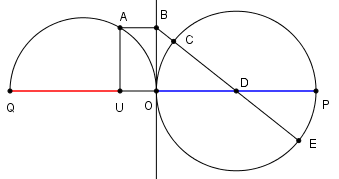
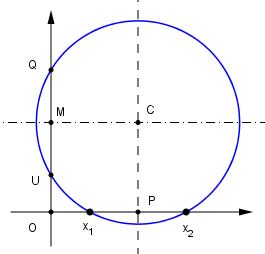
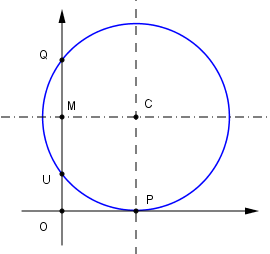
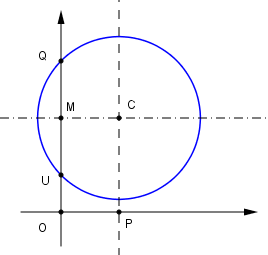
| Sia ancora OU un segmento di lunghezza unitaria, lo si prolunghi del segmento UQ e si tracci la semicirconferenza di diametro OQ. Da parte opposta rispetto ad O, prolungando QO di una quantità OP, si tracci la circonferenza di diametro OP avente centro in D punto medio di OP. Mandata per U la perpendicolare a QP che taglia la semicirconferenza in A. Da A si mandi la parallela a QP che taglia la normale in O a QP nel punto B. La retta BD taglia la circonferenza in C ed E. Dimostriamo che i segmenti BE e BC rappresentano le radici reali di una certa equazione di secondo grado. |
 |
|
|
 |
|
 |
 |