 |
|
 |
|
|
Charles-Ange Laisant ( x
1859 ) pubblicò nel 1887 un volume dal titolo "Théorie et
applications des Équipollences". Si trattava di una nuova
edizione, riveduta e ampliata, della "Exposition de la méthode des Équipollences" del 1874 cioè della traduzione francese fatta da Laisant di un'opera
del matematico italiano Giusto Bellavitis.
I due matematici furono messi in contatto epistolare dal matematico francese Nella prefazione al volume del 1887 Laisant ricorda il collega italiano. |
|
| l calcolo delle "equipollenze" è un antesignano del calcolo vettoriale, noi prenderemo in esame soltanto i primi due esercizi proposti da Laisant nell'edizione del 1887. |
| Due punti A e B, su una carta, sono separati da un fiume in cui la corrente ha una velocità costante, e i cui bordi sono rettilinei e paralleli. Il fiume si può attraversare soltanto in barca. Determinare il percorso più breve per andare da A a B. [Lo stesso problema compare anche in un volumetto del 1869 dal titolo "Sur le calcul des équipollences, méthode d'analyse géométrique de M. Bellavitis" di J. Hoüel]. |
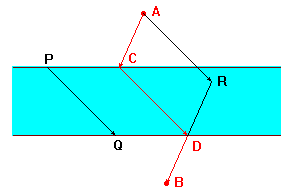 |
Tenuto conto della corrente, indichiamo con PQ il percorso che la barca effettua per attraversare il fiume. Traslato il vettore PQ in AR, il percorso più breve tra R e B è il segmento RB e il cammino più breve deve essere equivalente ad ARB. Se D è l'intersezione di RB con la riva del fiume riportiamo ancora PQ con l'estremo Q in D e troviamo il punto C sulla riva opposta. Chiaramente il percorso ACDB è equivalente al percorso ARB quindi è il percorso di lunghezza minima che è possibile effettuare. |
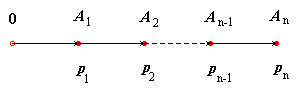
| Sono dati una serie di punti A1, A2, ... , An equidistanti e in linea retta. In ogni punto di essi è applicato un peso pari all'indice del punto. Trovare il baricentro di questi n punti. | ||||||
|
||||||
|
 |