Latus_Rectum

Nel 1875 Henri Brocard (1845-1922) riprese una precedente costruzione geometrica del parametro di una parabola da inserire nell'insegnamento secondario a completamento della costruzione che si deve a Germinal Pierre Dandelin (1794-1847). La parabola si ottiene sezionando con un piano con un cono circolare retto e nel 1876, il francese, Boleslas Alexandre Niewenglowski (1846-?) completò la trattazione dimostrando che la costruzione restava valida anche utilizzando un cono circolare ma non retto. La proposizione iniziale, che riportiamo sotto, si deve a Jacques Bernoulli (1654-1705).

«Un cono retto di secondo grado è tagliato da un piano ortogonale ad un piano principale, consideriamo una sfera concentrica al cono e tangente al piano secante: il piano tangente a questa sfera, mandato perpendicolarmente all'asse del cono, taglia il piano principale secondo una retta la cui parte intercettata dal cono e' uguale al parametro della sezione conica.»

(Jacques Bernoulli)

Le due dimostrazioni ottocentesche sono ottenute rispettivamente in tutto e in parte utilizzando la trigonometria. Noi preferiamo in entrambi i casi attenerci a delle dimostrazioni puramente geometriche.

Iniziamo disegnando la figura descritta nella proposizione di Bernoulli. Tracciamo un cono circolare retto di vertice C che, tagliato da un piano passante per l'asse di simmetria CH, determina il triangolo isoscele ABC. La sfera «concentrica al cono» ha il centro nel vertice C del cono. Il piano tangente in T alla sfera e' parallelo alla retta generatrice CB e taglia la superficie del cono generando la parabola di vertice V. Un secondo piano tangente alla sfera in K e perpendicolare a CH taglia il cono seconda una circonferenza il cui diametro DE appartiene al triangolo ABC ed ha una lunghezza pari al «latus rectum» della parabola.

In altri termini DE ha la stessa lunghezza della corda passante per il fuoco e ortogonale all'asse di simmetria della parabola stessa. Chiamata con p la distanza del fuoco dal vertice di una parabola con il fuoco in F(0, p) e direttrice di equazione y = - p risulta DE = 4p.

In primo luogo cerchiamo l'equazione della parabola generata dall'intersezione del piano tangente in T alla sfera, parallelo ad una generatrice e che taglia il cono.

Il piano taglia anche la base del cono secondo una retta ortogonale al diametro AB. Poiche' il cono è circolare ed e' possibile applicare ai segmenti QP, AP, PB contenuti nella base il II T. di Euclide dal quale risulta

Dalla similitudine dei triangoli isosceli AVP e ACB si ha

Mandata per il vertice V della parabola una retta parallela ad AB che interseca il lato CB in R dalla similitudine dei triangoli VCR e ACB si ottiene

Mandiamo da V a da A le perpendicolari alla generatrice CB che la tagliano in M ed N. Dalla similitudine dei triangoli rettangoli CVM e CAN risulta

Ma AN e' l'altezza del triangolo ACB rispetto alla base CB quindi, esprimendo l'area del triangolo sia rispetto alla base CB che rispetto alla base AB, si ha

Sostituendo nell'espressione del T. di Euclide le quantita' : AP, PB, CV, AN e semplificando si ottiene

Posti QP = x e VP = y si arriva all'equazione della parabola

Adesso formalizziamo la proposizione formulata da Bernoulli. Mandato il piano tangente alla sfera e perpendicolare all'asse del cono, questo piano taglia l'asse del cono nel punto K di tangenza con la sfera e determina sulla superficie del cono una circonferenza il cui diametro DE appartiene al piano del triangolo ABC. La lunghezza di DE si può dedurre dalla similitudine dei triangoli CDE e CAB

Ma DE e' uguale al «latus rectum» della parabola come risulta dal confronto con l'equazione della conica ricavata sopra.

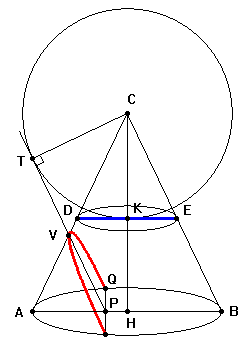
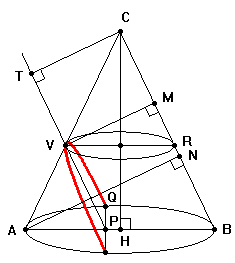
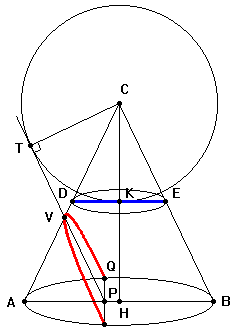
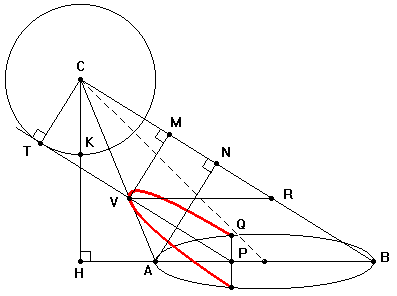
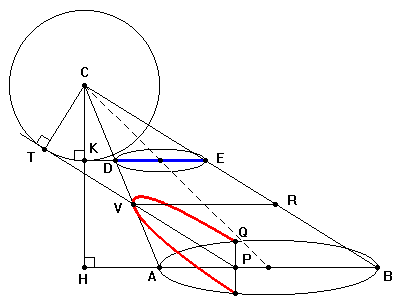
Nel caso il cono sia circolare, ma non retto, il risultato non cambia e non sono necessarie ulteriori dimostrazioni. La dimostrazione precedente si basa su tre elementi fondamentali: il T. di Euclide applicato sulla base circolare, le similitudini tra triangoli, la formula dell'area del triangolo. Tutti questi elementi rimangono immutati se il cono e' circolare ma non retto. Mantenendo le stesse notazioni si dovrebbe riprendere alla lettera quanto è stato esposto sopra anche perche' nel caso precedente non si e' mai utilizzato il fatto che il triangolo ACB e' isoscele. Quindi, anche in questo caso, DE è lungo quanto il «latus rectum» della parabola e vale