|
|
| Prenderemo in esame un
problema di massimo geometrico inserito come proposizione
XXXV nel testo di James Thomson: "Euclid's elements", third
edition, London, 1845. L'autore, di origine irlandese, fu
professore di matematica all'Università di Glasgow e padre
di William Thomson, 1st Baron Kelvin (1824-1907).
|
|
http://www.universitystory.gla.ac.uk |
| Lo stesso
problema fu ripreso e studiato anche da G. Polya in "Induction
and analogy in mathematics", Princeton University Press,
1955, (Volume I, pag. 122). Per ragioni di chiarezza
preferiamo l'enunciato nella forma data da Polya, mentre la
soluzione sarà sostanzialmente quella presentata da J.
Thomson. |
|


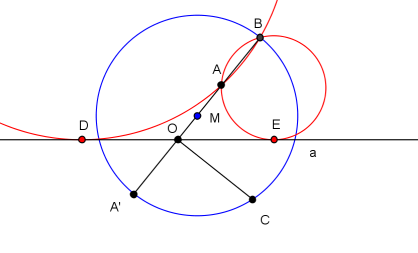 Fig.1
Fig.1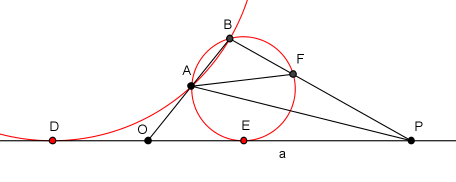 Fig.2
Fig.2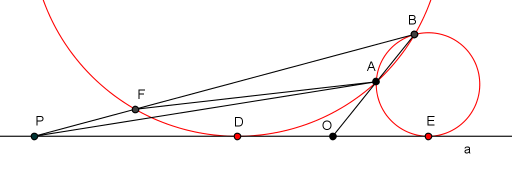 Fig.3
Fig.3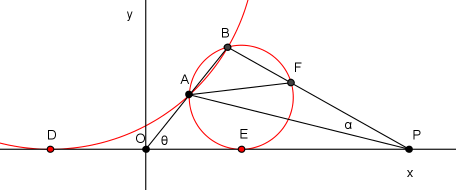 Fig.4
Fig.4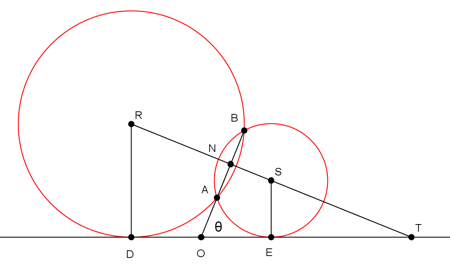 Fig.5
Fig.5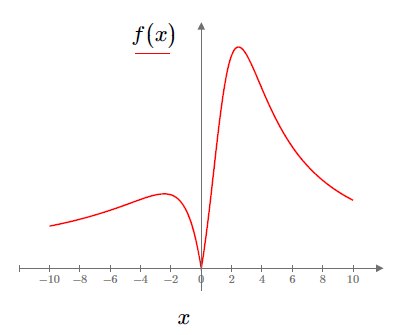 Fig.6
Fig.6