Medie e ... medie
  • Dati una retta r e un segmento AB che non appartiene ad essa, determinare sulla retta r un punto C tale che nel triangolo ABC  la base AB sia media aritmetica tra i lati CA e CB.

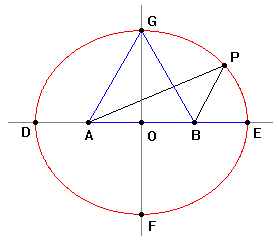
Posto  AB = 2a si ha  CA + CB = 2AB = 4a quindi il punto C appartiene necessariamente al luogo dei punti P la cui somma delle distanze da due punti fissi A e B č costante e vale 4a. Dunque il punto C, che per ipotesi appartiene alla retta r, deve appartenere anche ad una ellisse che ha per fuochi gli estremi del segmento AB. 

Detto O il punto medio di AB, fissato un sistema di assi cartesiani ortogonali con origine in O e asse delle ascisse solidale con il segmento AB, detti DE ed FG gli assi dell’ellisse si ha che il triangolo AGB isoscele sulla base AB e' equilatero:
 AB = GA = GB = 2a ,  quindi
inoltre OE = AB = 2a
dunque il luogo cercato risulta essere l'ellisse di equazione

Il problema ammette allora una, due o nessuna soluzione a seconda che la retta r sia tangente, secante o esterna all'ellisse trovata.
  • Costruire un triangolo rettangolo ABC di ipotenusa AB = k  in cui il cateto CB sia la media geometrica dell'ipotenusa  AB e dell'altro cateto AC.
Indicate con  AC = x e CB = y  (x, y > 0) le lunghezze dei cateti del triangolo rettangolo di ipotenusa  AB = k  e tenuto conto della relazione che esprime la media geometrica risulta

da cui segue una equazione di secondo grado in x della quale possiamo accettare soltanto la radice positiva

Dunque dato che  AC = x  si tratta di dividere l'ipotenusa AB = k  secondo una seziona aurea e prendere come  AC  la parte di ipotenusa di lunghezza maggiore.
 
Dal punto di vista geometrico sia ABDE un quadrato di lato AB, sia M il punto medio di AB : AM = MB  = a = k/2.
Con centro in M tracciamo una semicirconferenza di raggio ME  che interseca il prolungamento di AB in G.

La lunghezza del raggio ME si trova facilmente con il teorema di Pitagora e sottraendo da MG = ME  il segmento MB  = a =  k/2 si ottiene il segmento BG = GK = AC = x  di lunghezza cercata.