Percorsi in 3D

  
 
Dal libro Solution Book del 1888 di Benjamin Franklin Finkel (1865-1947) riprendiamo tre esercizi di geometria solida che si riferiscono a tracciati e figure nello spazio tridimensionale.
 
Una formica si trova nel vertice A di una stanza a forma di parallelepipedo di dimensioni AB = a, BC = b e C  = c con
a < b.  Determinare il percorso minimo che la formica deve fare per raggiungere il vertice opposto G della stanza.
Ribaltiamo le due pareti che hanno in comune il vertice G portandole sullo stesso piano del pavimento; in questo modo il punto G si deve sdoppiare in G e G' quindi tracciamo i due percorsi rettilinei AG e AG' , in un piano sono i percorsi più brevi che uniscono due punti assegnati.
Riassumendo

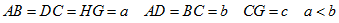Il triangolo AFG è rettangolo in F quindi

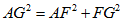da cui

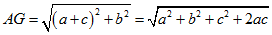Il triangolo  AHG' rettangolo in H

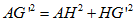ne risulta

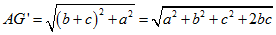quindi

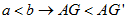e il percorso AG  è quello cercato.
Per definire meglio i due percorsi è possibile determinare in entrambi i casi i punti di passaggio dal pavimento alle pareti utilizziamo le similitudini fra i triangoli rettangoli della figura

 
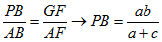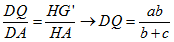Sul bordo di una aiuola circolare in due punti A e B in posizione diametralmente opposta sono stati posti i nel terreno due alberi di altezza AC = a e BD = b con a < b. Si chiede di determinare sul bordo dell'aiuola un punto P tale che le distanze CP e DP siano uguali.
 
 
 
 
 
 
 
 
 
Posto che

se è un P un punto della circonferenza allora il triangolo APB è rettangolo in P in quanto inscritto in una semicirconferenza. Inoltre le ipotenuse dei triangoli rettangoli CAP e DBP debbono essere uguali

da cui segue

e per riduzione si ottiene

Quindi

Tenuto conto che a < b  dalla seconda relazione si può ottenere facilmente la condizione di risolubilità del problema.

 
 
Le soluzioni in realtà sono due e sono simmetriche rispetto al diametro AB della circonferenza. Per evidenziarle da un punto di vista geometrico mandiamo un piano ortogonale al segmento CD e passante per il suo punto medio M. Tutti i punti del piano sono equidistanti dagli estremi del segmento CD e l'intersezione del piano con la circonferenza fornisce le soluzioni P e P' del problema.
 
 
Determinare il raggio del cerchio massimo che può essere inscritto in un cubo di lato l.
Si tratta del raggio della circonferenza inscritta nell'esagono regolare inscritto nel cubo assegnato. Il raggio r della circonferenza vale